一道函數(shù)零點(diǎn)問(wèn)題求解的探究

江蘇省高郵市三垛中學(xué) (225631) 楊葉飛

涉及函數(shù)零點(diǎn)的綜合問(wèn)題,一直是高考數(shù)學(xué)試卷中比較常見(jiàn)的一類(lèi)基本題型.此類(lèi)綜合問(wèn)題,設(shè)問(wèn)新穎創(chuàng)新,形式變化多端,可以合理融入函數(shù)圖象與性質(zhì)、函數(shù)與方程思想、函數(shù)與導(dǎo)數(shù)的應(yīng)用等內(nèi)容,交匯于函數(shù)模塊、導(dǎo)數(shù)模塊、不等式模塊等的基礎(chǔ)知識(shí),能全面有效考查學(xué)生的“四基”與數(shù)學(xué)能力,以及相應(yīng)的數(shù)學(xué)核心素養(yǎng)等,具有較好的選拔性與區(qū)分度,倍受各方關(guān)注.

1.問(wèn)題呈現(xiàn)

本題是一道含參函數(shù)的零點(diǎn)綜合問(wèn)題,零點(diǎn)問(wèn)題可以轉(zhuǎn)化為對(duì)應(yīng)方程的解或者兩個(gè)函數(shù)圖象交點(diǎn)的問(wèn)題,所以我們可以先考慮函數(shù)的性質(zhì);而本題還和絕對(duì)值、根式等知識(shí)巧妙聯(lián)系在一起,分類(lèi)討論和平方處理也是比較常用的解決方法.

2.問(wèn)題破解

解后反思：將函數(shù)的零點(diǎn)巧妙轉(zhuǎn)化為相應(yīng)方程的根問(wèn)題,進(jìn)而轉(zhuǎn)化為兩個(gè)函數(shù)圖象的交點(diǎn)個(gè)數(shù)問(wèn)題,利用函數(shù)f(x)在自變量取值范圍內(nèi)的單調(diào)性以及取值情況,利用函數(shù)的性質(zhì)加以巧妙的分類(lèi)討論是解決問(wèn)題的關(guān)鍵所在.挖掘問(wèn)題的本質(zhì),結(jié)合函數(shù)基本性質(zhì)的內(nèi)涵,兩者巧妙融合與轉(zhuǎn)化才能產(chǎn)生有用的效應(yīng).

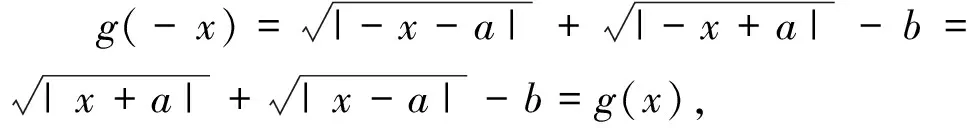
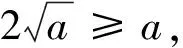
解后反思：根據(jù)函數(shù)奇偶性的基本性質(zhì),是解決問(wèn)題的關(guān)鍵所在.這里主要是借助具有奇偶性的函數(shù)有奇數(shù)個(gè)零點(diǎn),利用函數(shù)的對(duì)稱(chēng)性可知x=0必為該函數(shù)的一個(gè)零點(diǎn).涉及絕對(duì)值、根式等相關(guān)的方程求解,要注意分類(lèi)討論思想的應(yīng)用.

解法3:(函數(shù)圖象法)依題函數(shù)……