探究新情境中的離心率問題*

福建省莆田第十中學 (351146) 徐凡煒

《中國高考評價體系說明》指出,在試題命制層面,進一步強調情境化設計.試題情境是實現考查內容和考查要求的載體,學生解決問題時,需要在理解與提取、分析與推理、歸納與表達的基礎上,尋求解決問題的途徑.本文以三類情境試題為例進行剖析,旨在引導學生合理解讀試題情境,聯想求解方法,探索離心率問題的解題規律.

1.課程學習情境

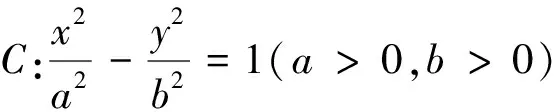
分析：本題情境源于“雙曲線”和“解三角形”的課程學習,創設的試題情境屬于學習關聯情境.考查了雙曲線的定義、余弦定理及向量的坐標運算等必備知識,考查了邏輯思維能力、運算求解能力、空間想象能力等關鍵能力,考查了直觀想象、數學運算等核心素養.

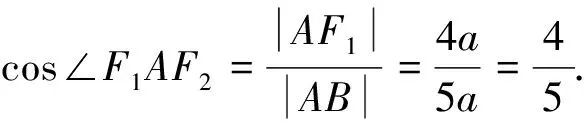
評析：雙曲線過焦點的三角形的問題解決的關鍵是充分利用雙曲線的定義,結合勾股定理與余弦定理得到關于a,b,c的齊次方程,從而得解.

變式(2018年高考全國卷Ⅱ·文11)已知F1,F2是橢圓C的兩個焦點,P是C上的一點,若PF1⊥PF2,且∠PF2F1=60°,則C的離心率為( ).

2.探究創新情境

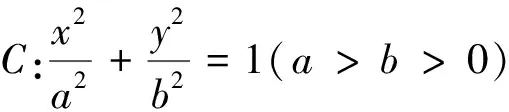
分析：本題以“橢圓的標準方程與簡單的幾何性質”為試題情境,涉及的知識源于學生已有的學習體驗,其中橢圓定義的表述方式源于學生的學習儲備,故所創設的試題情境屬于綜合聯想情境.考查了橢圓的定義、向量的數量積等必備知識,考查了邏輯思維能力、運算求解能力、空間想象能力等關鍵能力,考查了直觀想象、數學運算等核心素養.

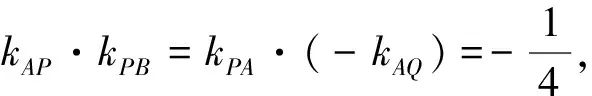
評析：本題常規方法是設P,Q兩點坐……