基于任務群的深度學習設計
——以2019人教A版的一道習題為例

廣東省廣州市天河外國語學校 (510630) 劉惠梅

高中數學新教材中很多習題有著極強的“代表性”與“穿透性”,教師若能積極開展對教材習題的研究,創設合理的任務群,以“最近發展區”為平臺,在課堂中提出高價值的問題,就能引導學生仔細觀察、大膽猜想,嚴謹推理,不斷拓展學生的認知,提升四基四能.

本文以2019版人教A版選擇性必修第一冊的一道習題為例,通過聚焦任務群,讓學生經歷從特殊到一般、從確定性到完備性、從順推到逆推的探究過程,體驗研究數學問題的普適性方法,落實數學核心素養.

具體研究思路為:

一、問題

題源(2019版人教A版選擇性必修第一冊第三章“圓錐曲線的方程”P128習題3.2第11題)M是一個動點,MA與直線y=x垂直,垂足A位于第一象限,MB與直線y=-x垂直,垂足B位于第四象限.若四邊形OAMB(O為原點)的面積為3,求動點M的軌跡方程.

圖1

設計意圖：題源來自于新教材的課后習題,習題通常蘊含了很多一般性規律.老師要善于鉆研教材,強化思維遷移,引導思維向廣度和深度拓展延伸,引導學生從解題到解決問題的轉變.此題結論是否具有一般性?

二、猜想

任務1 題源中直線y=x與y=-x恰好是動點M的軌跡(即雙曲線)的兩條漸近線,這個結論是否可以推廣到以下一般情況?

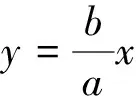
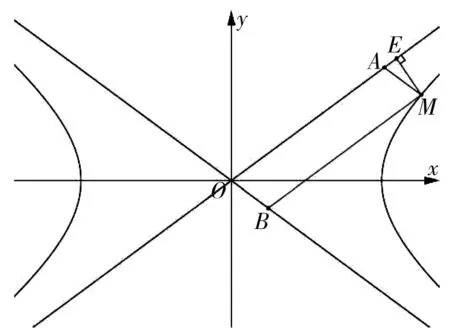
圖2

設計意圖：任務1將題源中的特殊情況通過大膽猜測、嚴格證明推廣到一般的結論,學生經歷從特殊到一般的過程,通過發現隱藏在表象中的一般性結論,實現多題歸一.

三、完備性探究

任務2 任務1中……