強化情境創設 培養創新精神

江蘇省鎮江高等職業技術學校 (212016) 李 文

《普通高中數學課程標準》(2017年版)在“學業水平考試與高考命題建議”中明確指出:數學命題時,應有一定數量的應用問題,問題情境的設計應自然、合理.這里的問題情境主要是指現實情境、數學情境、科學情境等,是體現數學學科核心素養的主要方面,也能充分體現“立德樹人”的教育目標.本文結合一些模擬題中對數學情境創設的不同類型的設置情況,加以實例剖析.

1 夯實基礎性

以實際問題情境為數學背景載體,滲透入相應的數學基本概念與定義、公理或定理、數學公式與數學思想方法等基礎性知識和能力的考查,引導學生重視數學學科的基礎內容,夯實學生的數學基礎知識,體現高考數學試題的基礎性.

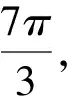
A.25-00 B.35-00 C.42-00 D.70-00

分析：根據密位制的定義,利用扇形面積公式先求出圓心角,再根據密位制的定義換算即可.

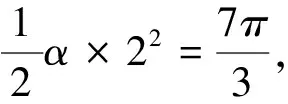
評注：通過數學情境設置,結合扇形的面積公式、任意角的三角函數的定義以及密位制的定義等,結合三角函數這一基本性數學知識來巧妙設置創新數學情境,借助相應的數學知識來分析與解決問題.

2 立足綜合性

選擇現實生活、生產工作中的現實案例,融入學生的現有認知水平以及數學層次,抽象概括地合理創設數學問題情境,融合數學知識與數學思想方法,綜合數學多模塊知識或高中多學科知識之間的交匯,考查綜合知識與能力,體現高考數學試題的綜合性.

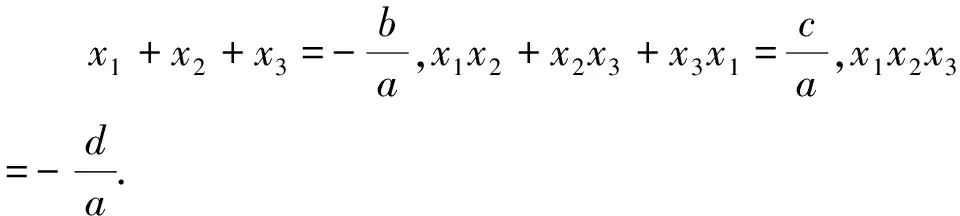
A.2x1-x2=0 B.2x1-x2-1=0

C.2x1+x2+1=0 D.2x1+x2=0

分析：以數學文化為情境……