智能垃圾回收下收集中心選址-路徑二層優化

馬艷芳，賈佳鵬，李宗敏，閆 芳

1.河北工業大學 經濟管理學院，天津 300401

2.四川大學 商學院，成都 610064

3.重慶交通大學 經濟管理學院，重慶 400074

4.重慶市環衛集團，重慶 401137

《“十四五”城鎮生活垃圾分類和處理設施發展規劃》指出要加快建立城鎮生活垃圾處理系統，并鼓勵依托物聯網等新興技術提升垃圾處理能力。國內已有不少公司利用智能垃圾箱開展垃圾回收業務，如“小黃狗”“愛家物聯”“綠島”等智能垃圾箱。物聯網技術能夠對垃圾箱狀態進行跟蹤監測[1-2]，將信息傳輸到在線平臺[3]，當垃圾量達到閾值時平臺發出預警信號，根據平臺信息優化回收路徑確保容量不足的智能垃圾箱得到及時清理。而下游收集中心作為回收車輛終點，其位置決定回收系統的有效性，選址不當將產生高額運輸成本。因此，收集中心選址和回收路徑規劃整合研究極大影響垃圾回收的成本和效率。

智能垃圾箱是一種利用物聯網等技術獲取垃圾桶內相關信息的智能環保設備，如何利用這些信息實現資源高效利用成為亟待解決的問題。為了克服這一問題，Ramos 等[4]提出智能垃圾收集路徑（smart waste collection routing，SWCR），依據其收集閾值先選擇需要訪問的垃圾箱再確定最佳收集順序。此外，Gutierrez 等[5]依據傳感器存儲的數據庫選擇要收集的垃圾桶，采用路徑優化算法計算出最優的路徑，以使行車距離最小化。Gilardino等[6]根據各收集點垃圾量和每輛車的可用工作時間優化收集路徑。物聯網背景下智能垃圾箱逐漸普及，優化回收路徑時充分利用其信息量大和可預警等特點可實現資源高效利用。

表1 總結了LRP 及其在垃圾回收領域的相關研究。可以看出有關LRP研究多采用雙層結構，由不同層次多個參與者參與聯合決策，隨著服務多樣化和專業化的發展，大多企業選擇將物流作業外包給第三方企業，如生鮮外包配送[7]，充電基礎設施選址-路徑問題[8]等。但垃圾回收背景下的LRP相關研究較少，建立雙層模型來考慮不同決策主體進行聯合優化的研究更少。除此之外，LRP是NP難問題，多數文獻都采用啟發式算法進行求解[7-15]。其中遺傳算法應用尤為廣泛，但部分文獻遺傳操作較為簡單[9-10]，多采用單一初始化方式，即隨機初始化[7，10-11，15]或啟發式初始化[8，14]，采用單點變異[7，11]或單點交叉[10，15]等算子進行交叉變異操作，并通過傳統概率復制來選擇新種群[10-11，14]。此外，已有文獻采用聚類算法分配需求[10，15-16]，但忽視了容量約束。本文提出改進的遺傳算法：使用多種初始化方法，在保持種群多樣性的同時尋求較優的初始解；引入最優成本路線交叉算子和反向變異算子，減少回收車輛的使用數量，降低總回收成本的同時[17-18]，增加種群多樣性避免陷入局部最優；并在此基礎上通過精英選擇策略保留優質種群加快迭代速度。

表1 相關文獻特征Table 1 Characteristics of relevant literature

綜上，目前關于LRP 的研究已取得了一定的成果，但在收集中心選址及智能垃圾箱回收路徑規劃方面仍存在不足之處：一方面，將垃圾處理點選址與回收路徑問題整合規劃的研究較少，且少有學者研究智能垃圾箱回收問題；另一方面，多數研究基于遺傳算法求解雙層LRP模型，但存在采用單一初始化方式和個別效果較差的算子等問題，因此有必要對此進行改進。基于此，本文研究智能垃圾回收下帶容量約束的雙層選址-路徑整合優化問題，考慮了上下層不同決策主體之間復雜關系，應用智能垃圾收集路徑方式進行路徑規劃，設計改進的遺傳算法進行求解，最后通過算例分析驗證了模型和算法的有效性和適用性。

1 問題描述

本文研究一個具有雙決策主體的容量有限的選址-路徑多主體優化問題（capacitated location-routing problem，CLRP），建立了雙層規劃模型來描述該問題。在該模型中，上層決策者依據給定的收集中心備選點進行選址決策；下層決策者首先確定需要收集的智能垃圾箱，當垃圾箱內垃圾量大于閾值說明垃圾箱容量不足亟待收集，反之則不需收集，其次依照上層決策來規劃收集路線以確保整體優化。

在實際生活中，由于智能回收企業的業務布局范圍較廣，如“小黃狗”和“愛家物聯”分別進駐48、36個城市等，故多是負責智能垃圾箱運營和維護等工作，而清理收運則多是雇傭當地的物流運輸公司來負責。智能回收企業在建立回收系統過程中要均衡各方面成本以實現總成本最低，而外包物流公司只關心其運輸相關成本，故而在進行收集中心選址和回收路徑規劃決策的過程中，存在兩個決策主體，分別是智能回收企業（上層決策者）和外包物流公司（下層決策者），但二者間存在復雜的沖突合作關系，如圖1所示。

首先，智能回收企業決定收集中心的位置，將直接影響外包物流公司的回收路線計劃。智能回收企業做出選址決定后，外包物流公司才能根據閾值確定容量不足的智能垃圾箱，從而規劃最優的收集路線以確保運輸相關成本最小化。其次，外包物流公司的路徑規劃又將反作用于智能回收企業的選址決策。外包物流公司規劃好回收路徑，將會產生運輸成本和車輛啟動成本等，這又將會影響企業總經濟目標的實現，從而影響選址決策。顯然，雙層CLRP模型中兩個主體決策行為相互影響。雖然智能回收企業和外包物流公司都尋求獨立地最小化其目標，但又都受到彼此行為的影響，這些決策的相互影響既體現在目標函數中，也體現在約束條件中。

依據Baldacci 等[19]提出的雙商品流公式，建立多倉庫的選址-車輛路徑模型。其中車輛每條路線都涉及兩種流：一種是車輛從收集中心出發，最終到達其副本時的負載，另一種是同一車輛上對應的空載。將該公式引入VRP 模型，可提高精確算法或啟發式算法求解的收斂速度[20-21]，也可用于建立LRP模型，如爆炸性廢物回收系統的選址-路徑問題[22]。

雙商品流動公式中所提出的基本流動規律如圖2所示，其中車輛容量Q=1 000，9 個待收集的智能垃圾箱、兩輛車和一個收集中心。雙商品流公式使用兩個流變量yij和yji來模擬車輛穿過邊(i,j)時所攜帶的廢棄物的流，即每條路線由兩條路徑定義：一條由表示車輛載荷的yij流變量表示從節點0到節點n+1 的路徑P1；從節點n+1 到節點0的第二條路徑P2由表示車輛空白區域的流變量yji表述。因此，兩種流的總和等于車輛容量，例如y36+y63=1 000。具體來說，以節點1、3、6和8 之間的流動為例，可以注意到：（1）節點3 的總流出量減去總流入量等于該節點產生的廢棄物量的兩倍，即(y31+y36)-(y13+y63)=2m3；（2）收集中心副本n+1 的總流出等于剩余車輛容量，即y(n+1)8=Q-y8(n+1)；（3）收集中心副本n+1 的總流入量等于裝載的廢物總量，即y8(n+1)=m1+m3+m6+m8；（4）yij和yji變量取可行值，其中y13+y31=Q×x131×g1。

圖2 雙商品流示意圖Fig.2 Two-commodity flow formulation representation

2 模型建立

針對以上描述，介紹了建立模型所需的假設條件和參數符號，并給出數學模型。

2.1 模型假設

建立雙層選址-路徑問題的數學模型所需假設條件如下所示：

（1）候選收集中心的數量、地理位置、固定成本已知。

（2）各收集中心容量已知，分配給各收集中心的總需求量不能超過設施的容量限制。

（3）配送車輛均為同質車輛，固定成本和容量已知，各運輸路徑上車輛載重不能超過容量限制。

（5）每處收集點（需要收集的智能垃圾柜）的地理位置和所產垃圾量已知。

（6）各節點間距離按照歐氏距離計算，運輸車輛單位距離運輸成本已知。

（7）每個站點每次只能被一輛車收集一次，收集車輛從收集中心出發并最終返回收集中心。

2.2 參數符號

集合

I：智能垃圾箱集合I={1,2,…,n}；

C：收集中心備選位置集合C={1,2,…,c}；

：收集中心的復制點{1,2,…}；

G：智能垃圾箱和收集中心的集合G=I?C?

V：同質車輛的集合；

指標和參數

i/j/m：智能垃圾箱站點和收集中心的索引i,j,m∈G；

k：車輛的索引k∈V；

n：智能垃圾箱總數，即垃圾產生站點總數；

c：備選收集中心總數；

l：同質運輸車輛總數；

mi：智能垃圾箱i處所產生垃圾的質量i∈I；

Q0：收集中心的額定容量；

Q：車輛的額定載重質量；

FCi：收集中心i的固定開放成本i∈C；

VCi：收集中心i的每單位垃圾的處理成本i∈C；

FVk：啟用車輛k的固定成本；

c0：所用車輛的單位運輸費率；

dij：節點i和節點j之間的距離；

φi：智能垃圾箱回收閾值。

決策變量

hi：0-1變量，如果候選收集中心i∈C開放，則為1，否則為0；

gk：0-1變量，如果車輛啟用k∈V，則為1，否則為0；

zik：0-1變量，如果車輛k∈V訪問點i∈I，則為1，否則為0；

yij：表示點i到點j的流量，為非負數；

xijk：0-1變量，如果車輛k訪問邊(i,j)，則為1，否則為0。

2.3 數學模型

2.3.1 上層規劃

上層規劃由智能回收企業確定收集中心選址，確保由收集中心的開設成本、運營成本、車輛運輸成本和車輛固定成本組成的總成本最小化。上層公式如下：

目標函數（1）是總經濟成本最小化，包括收集中心開放成本、操作運營成本、車輛運輸成本和車輛固定成本。由于每個行程都被定義為包含兩條路徑的車輛路線，因此車輛運輸成本需要除以2以獲得真實的運輸成本。約束（2）保證收集中心的總數至少為一個，且滿足約束（3）確保解滿足收集中心容量限制。

2.3.2 下層規劃

經過分析，下層模型是一個車輛路徑規劃問題。因此，車輛運輸相關成本最小化是外包物流公司的目標，包括車輛運輸成本和車輛固定成本。其數學公式描述如下：

目標函數式（5）表示外包物流公司的總運輸成本最低；約束（6）確保每個點的流出量減去流入量等于每個點中廢棄物量的兩倍；約束（7）確保復制點n+1 的總流入等于所收集的智能垃圾箱中總廢物量；約束（8）確保復制點總流出量等于車隊的剩余容量；約束（9）保證實際路徑的裝載總量小于或等于車隊的運力；約束（10）和（11）根據回收閾值篩選容量不足的智能垃圾箱，并確保這些需要收集的智能垃圾箱僅由一輛車提供服務，本文根據智能垃圾箱i前10 天垃圾投放平均值來估計其每日預期投放量αi，并定義回收閾值φi=(1-αi/q0)×q0，其中q0為智能垃圾箱額定容量，當智能垃圾箱現存垃圾量mi大于φi時，其容量不足難以容納次日投放量，故該智能垃圾箱需要進行收集；反之則不需收集該垃圾箱；約束（12）表示每個點都有兩條路徑；約束（13）確保車輛離開收集中心時是空載；約束（14）表示車輛必須完全清空它訪問的所有垃圾箱；約束（15）確保啟用的車輛數量不超過車隊總數；約束（16）連接了變量yij和xijk，表示保證如果有車輛訪問邊(i,j)，其流量之和必須等于車輛的通行能力；約束（17）～（20）避免產生非可行解；約束（4）和（21）～（24）給出變量的定義域。

2.3.3 全局模型

垃圾收集的選址路徑問題可以分為兩個層次：智能回收企業為上層決策者，外包物流公司為下層決策者。在BP 問題中，底層模型也是全局模型的約束。根據2.3.1和2.3.2小節，可以得到全局模型如下：

在全局模型中，智能回收企業決定開設哪個收集中心（決策變量hm），以實現總成本的全局最小化。外包物流公司先根據閾值確定亟待收集的智能垃圾箱，進而在智能回收企業決策的基礎上進行路徑規劃。然而，路徑規劃對智能回收企業的成本最小化目標有著重要的影響。全局模型描述了垃圾回收選址-路徑模型中存在沖突和協調的智能回收企業與外包物流公司之間的相互影響。

2.4 公式有效性

由于雙商品流公式僅用于下層路徑模型，故而本節證明將該公式引入CVRP模型的有效性。

首先，證明CVRP 的解可滿足雙商品流公式。當CVRP 求解得到回收路線時，其變量xijk和yij滿足如下約束：

不妨將不屬于上述CVRP解的邊都設置成xijk=0，yij=yji=0，此時上述所定義的兩個變量顯見是雙商品流公式的可行解。

3 求解算法

選址路徑多主體優化問題求解難度非常大，屬于強NP難問題。目前大多采用啟發式算法[7-15]求解，如遺傳算法，粒子群算法等，本文提出了一種改進的遺傳算法來求解雙層規劃問題。首先，結合多種初始化方式以獲得初始解，上層聚類獲得初始選址方案，下層采用隨機和節約里程算法獲得初始路徑，確保種群多樣性同時尋求更優良的初始解；其次，將最優成本路線交叉、反向變異和精英選擇相結合，改善算法局部搜索能力的同時檢查可行性約束。

3.1 編碼與解碼

上述問題包含垃圾收集中心選址和回收路徑兩個子問題，用三個向量來表示一個完整的解，第一個向量為車輛向量，第二個是順序向量，第三個表示車輛所屬收集中心向量。假設有8 個備選配送中心，編號為1，2，…，8；可支配車輛4 輛，編號為1、2、3、4；待收集的智能垃圾箱16個，編號為1，2，…，16，回收方案如下：

首先，收集中心向量表示上層選址方案，即選擇2和6，且車輛1、3 從收集中心2 出發，車輛2、4 從收集中心6 出發。其次，確定需要收集的智能垃圾箱，不難看出編號為7和13的智能垃圾箱未達回收閾值，不需要回收。最后，在上層決策的基礎上進行回收路徑規劃，智能垃圾箱編號對應位置的車輛向量值表示收集該垃圾箱的車輛，如客戶1、6 和16 由車輛4 收集；車輛向量對應的順序向量值表示車輛收集的先后順序，如車輛4先收集垃圾箱1，其次是垃圾箱6，最后是垃圾箱16。因此，上層解碼后得到選址方案為收集中心2和6；下層解碼后得到回收路線，整合上下層解碼得到最終問題的解如下：

3.2 初始化與適應度函數

上層采用聚類算法確定初始選址方案，下層則采用隨機和節約里程算法生成初始車輛路徑，其中80%的初始種群是隨機的，另外20%用節約里程算法生成[23]。Jammeli 等[16]采用“聚類優先，路徑其次”的分層方法來求解回收過程中的分配和路徑方案，Mendoza等[24]使用節約里程算法生成初始路徑方案來加速算法收斂。在前人研究的基礎上，采用多種初始化方法以期得到一個良好的初始化種群，盡量避免計算資源的浪費，也希望種群具有良好的多樣性，降低算法復雜度且不易陷入局部最優。

上層采用聚類算法確定初始選址方案，將多收集中心路徑問題轉化為單收集中心路徑問題，從而大幅降低問題的復雜度。比較常用的方法是根據智能垃圾箱與收集中心間的距離進行分類，但這種方法沒有考慮收集中心容量約束，導致結果質量偏低。為解決這一問題，本文聚類算法考量收集中心容量約束，具體步驟如下：

（1）計算所需最少收集中心個數knum，在C中隨機選取knum作為收集中心，其中。

（2）計算各智能垃圾箱i∈I到knum個收集中心的距離，并將其分配給最近的收集中心記為Cknum。

（3）計算每個集合Cknum中的智能垃圾箱數量，并按降序排序。選擇排名最高且未被選中的收集中心開放。

（4）根據收集中心容量回收智能垃圾箱。依次累計計算智能垃圾箱i∈Cknum的垃圾量直到超過收集中心容量；Cknum中未被分配的客戶將被分配到下一個開放的收集中心。

節約里程數的計算公式為ΔCij=C0i+C0j-Cij。公式的意思是i到j的節約里程數為收集中心到i的距離加上收集中心到j的距離減去i到j的距離。節約里程法計算步驟如下：

（1）作運輸里程表，列出收集中心到用戶及用戶間的最短距離。

（2）按節約里程計算公式求得相應的節約里程數ΔCij。

（3）把節約的行程值從大到小排序，放到list中。

（4）檢查各連接點可行性，按照list的順序連接各客戶結點，最終確定配送線路。

適應度函數要結合求解問題本身而定，每個染色體的適應度值反映目標值，據此判斷個體的優劣，從而來進行選擇操作。上層決策目標為建造、服務和運輸總成本最小，每個備選點的建設成本已知，下層目標為運輸相關成本最小，根據雙層規劃理論，上層決策者在決策中占主導地位，上層目標是雙層規劃中的主導目標。當滿足各約束時，目標函數如公式（1）。

考慮到車輛和收集中心容量約束，對超出容量約束的染色體添加一個足夠大的懲罰值，避免生成非可行解。此外，由于模型為最小化組合優化問題，目標函數值越小，對應的染色體適應度越高，解越優良。因此，以上層目標函數值與懲罰函數值之和的倒數作為適應度函數。適應度函數如下：

其中，fi表示第i條染色體的適應度值，F1i表示對應的目標函數值，P1和P2分別表示車輛超載或收集中心容量不足時產生的足夠大的懲罰值，當滿足約束時，P1=0,P2=0。

3.3 算法流程

改進的GA算法在標準遺傳算法基礎上進行改進，引入最優成本路線交叉算子和反向變異算子確保種群多樣性的同時增加算法的搜索能力，結合精英策略避免優秀個體丟失。改進GA算法流程如圖3所示。

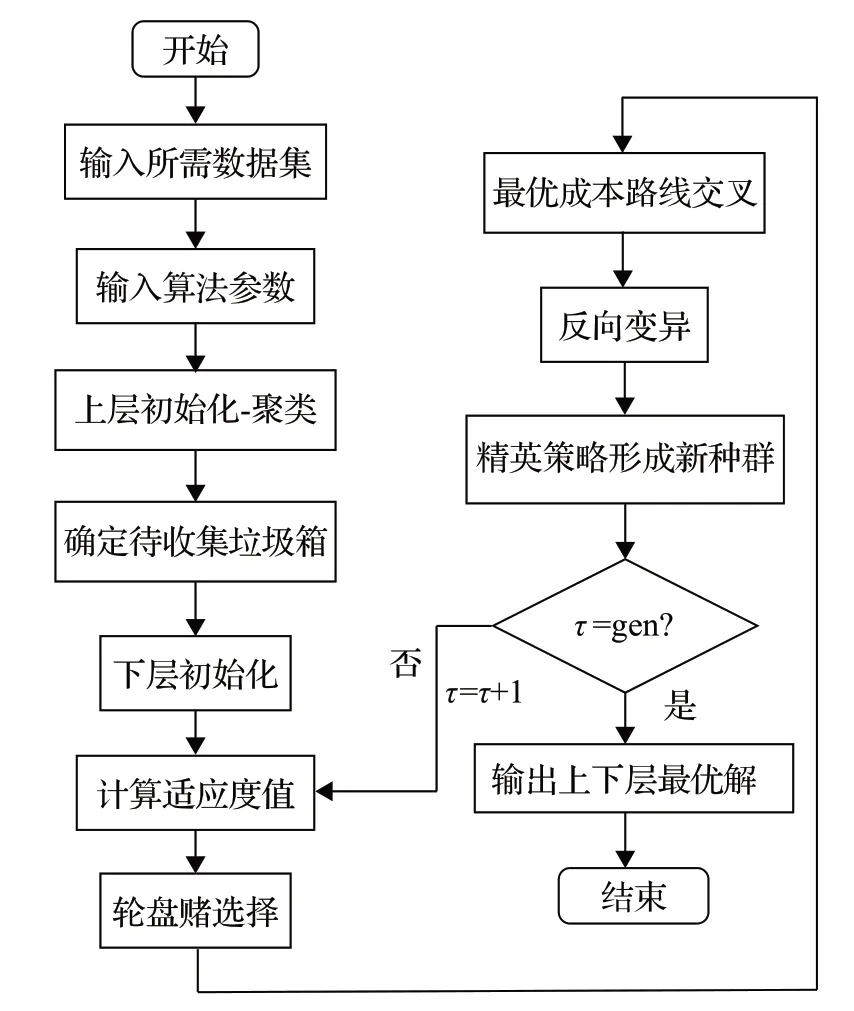
圖3 GA-pro算法流程圖Fig.3 Flowchart of GA-pro

算法步驟概括如下：

步驟1輸入計算數據，設置交叉率、變異率等參數，并初始化種群。其中，初始化種群分為兩部分。上層依據備選智能垃圾箱信息應用聚類算法獲得初始收集中心選址方案；下層依據回收閾值選定亟待收集的智能垃圾箱，再通過隨機和節約里程算法獲得初始回收路徑。

步驟2計算各個個體的適應度值，進行選擇、交叉和變異操作，并應用精英策略形成新種群防止最優解退化。其中，對交叉和變異操作進行改進，采用最優成本路線交叉算子和反向變異算子來增加算法的局部搜索能力。

最優成本路線交叉：由于交叉操作過程中父代隨機刪除一條路徑，并在滿足容量約束的前提下將刪除的基因重新插入到局部最優位置，最后將所得基因按順序替換父代染色體基因確保編碼為0 的位置不變從而得到子代，因此，該算子可在最小化車輛數量和成本的同時檢查容量約束[17-18]。用規模為11 的任意問題實例來解釋該交叉過程，如圖4 所示。首先，根據所給父代P1 和P2確定各個車輛路徑，如步驟（a）所示P1有三條車輛路線，即3→4→2、6→8→1、5→7，從父代中隨機各選擇一條路徑。在本例中，選擇P1包含垃圾箱5和7的第三條路徑，以及P2 中包含垃圾箱2 和4 的第二條路徑。其次，從P1 中移除P2 所選路徑包含的垃圾箱。如圖4 步驟（b）所示，從P1 中移除2 和4，從P2 中移除5 和7。隨后，將被刪除的垃圾箱在不違背容量約束的情況下，一個接一個地重新插入到局部最優位置如步驟（c），以使整個行程的總成本最小化，其間，插入的順序是隨機進行的。最后，確保0 位置不變的情況下，將得到的染色體按順序替換父代染色體基因獲得子代染色體。

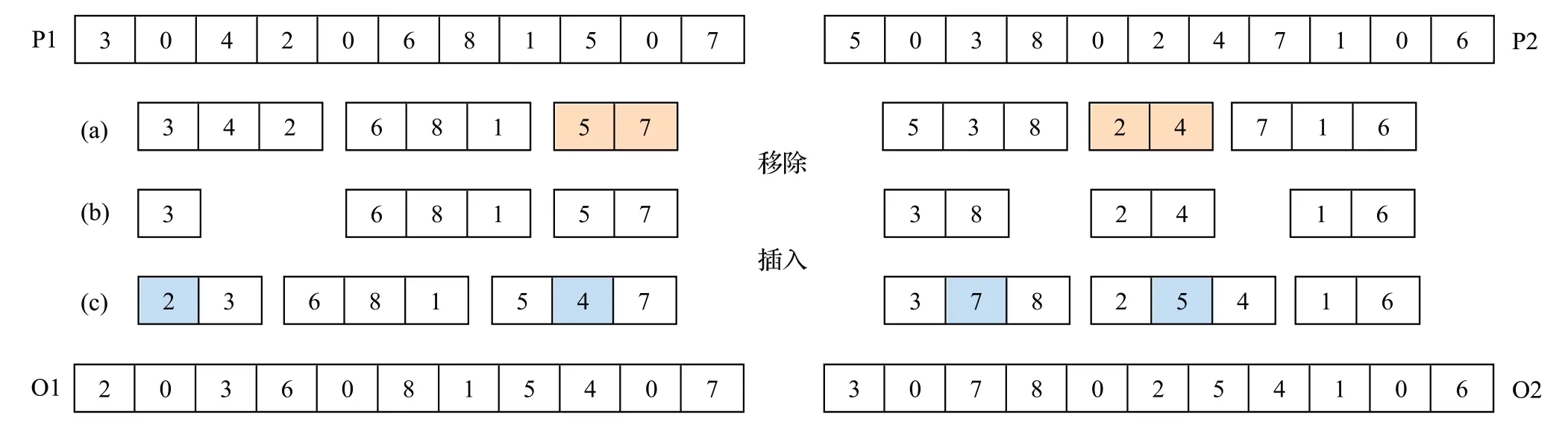
圖4 最優成本路線交叉Fig.4 Best cost route crossover operator

反向變異：隨機選擇兩個位于親本染色體上的變異位置，然后將兩個位點之間的所有基因進行反轉，得到一個新的后代染色體，以維持種群的多樣性，改善遺傳算法的局部搜索能力[25]。

步驟3判斷是否滿足終止條件，滿足則輸出最優解，否則返回步驟2。

4 基準案例測試

首先，選用兩組LRP 經典基準案例集Prins 等[26]和Barreto等[27]進行測試來驗證改進的GA算法（GA-pro）性能，兩個案例集均可在http：//prodhonc.free.fr/Instances/instances下載；其次，結合模擬實際案例，證明雙層模型的合理性。本文構建的數學模型與算法用MATLAB R2014b 編碼，在Lenovo 小新-14API 2019 計算機運行，具體配置為2.10 GHz Ryzen 5-3500U 處理器，操作系統為Windows 10 64位。

GA算法涉及的參數主要有迭代次數、種群規模、交叉概率、變異概率等參數。通過一定的實驗測試和文獻參考[7]，設置迭代次數為500 代，種群規模為50，變異概率為0.2，交叉概率為0.75。

選取Prins 等提出的算例中客戶數為20、50、100 三種規模大小的總計24 個案例和Barreto 所提出的12 個算例進行測試，并與求解結果較好的GAPSO[7]和BSA算法[28]進行對比分析，且調整算法目標成本與各案例中目標成本相匹配以更具備可比性，求解結果如表2和表3所示。BKS為基準案例已知最優解，GA-pro所得結果為將各案例運行10次的最優結果，Gap為各算法最優解與BKS的差距百分比。

表2 Prins案例求解結果Table 2 Solution results of instance Prins

表3 Barreto案例求解結果Table 3 Solution results of instance Barreto

表2 為Prins 的24 個LRP 基準案例求解結果，其中GA-pro在12個案例中求得了最優解，另12個案例絕大多數也可獲得近似最優解。當顧客規模小于100 時，GAPSO均能求得最優解，而GA-pro稍遜。而在顧客規模等于100 的12 個案例中，BSA 有4 個案例求得最優解，3個案例結果較另兩個算法更優；GAPSO和GA-pro僅求得一個最優解，且各有2、3個案例求解結果優于另兩種算法。GA-pro在大中小規模案例中的表現均介于兩種對比算法之間，且與最優解BKS 的差距均值僅為0.419%，由此可見，GA-pro可以在一定程度上較好地解決CLRP問題。

由表3 可以看出，BSA 算法整體表現良好，在大規模算例中求得結果更為接近BKS。相比之下，GA-pro求解大規模算例的能力相對較弱，當顧客規模小于50時都能找到最優解，在中大規模算例中雖不能全部找到最優解，但是與其他算法差距不大。從整體來看，GA-pro 在中小規模案例中表現優于BSA，在大規模案例中表現優于GAPSO，具備一定的競爭力。

5 模擬案例

5.1 案例描述

為驗證本文模型的合理性和適用性，擬選用4個備選收集中心，以滿足50 處智能垃圾箱的回收需求。備選收集中心的位置、容量和建設成本如表4所示。智能垃圾箱位置、需求量和回收閾值如表5 所示，僅列出前15個智能垃圾箱相關信息為例。根據實際情況和社會經驗，使用的其他參數設置如下：車輛容量為1 000 kg，每輛固定成本為400 元，每千米運輸費用為0.75 元，其他參數設置同第4章。

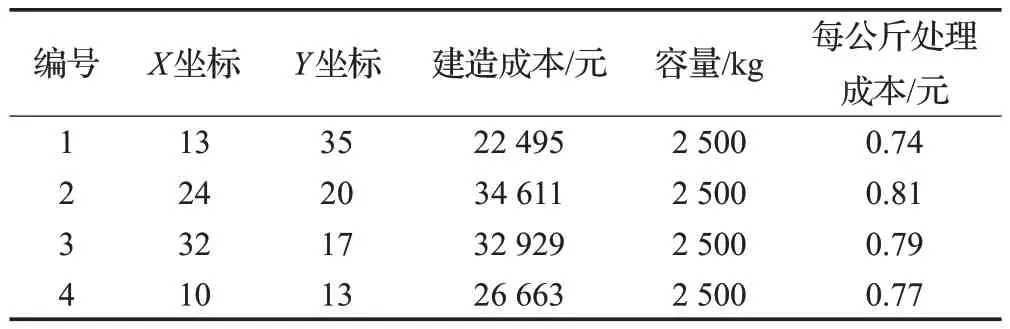
表4 備選收集中心信息表Table 4 Information sheet for alternative collection center

表5 智能垃圾箱部分信息表Table 5 Information sheet for some smart bins

5.2 主從二層結果分析

5.2.1 智能垃圾收集模式

基于上述數據，應用智能垃圾收集模式，即先根據閾值確定需要收集的垃圾箱再對其進行路徑規劃的方式，并運用前文提出的改進遺傳算法求解本案例，運行算法30次，選擇其中最佳優化結果。結果顯示，開放編號為3 和4 的收集中心，當日待收集垃圾箱共24 個，收集中心3 發出兩輛車，收集中心4 則發出一輛車進行收集，總計成本約為79 437 元，解碼后，上下層路徑優化方案如下：

5.2.2 傳統收集模式

本文還求解相同條件下傳統收集方式的選址路徑方案（即每日收集全部垃圾箱）。傳統收集方式選擇開放編號為1和4的收集中心，且各發出兩輛車，總計成本約為88 700元，解碼后，上下層的路徑優化方案如下：

5.2.3 兩種模式對比分析

觀察以上結果可以看出兩種收集模式下所開放收集中心不同，盡管收集中心1的建造成本及單位運營成本在所有備選中心中最低，但在智能垃圾收集模式下顯然不是最佳選擇，無法使總成本達到最小。這是由于所設閾值是依據各處垃圾箱往日投放量來計算，而每處垃圾箱容量相同，使得一部分垃圾箱收集次數較為頻繁，而收集中心3相比于收集中心1處于此類垃圾箱較為密集的位置，更大可能降低運輸成本。

兩種收集模式各成本對比如表6 所示，經比較可知，智能垃圾收集模式相比于傳統收集模式節約成本約9 263元。智能垃圾收集模式下僅開放成本比傳統收集模式高，但其余三項成本皆低于傳統收集模式，其中運輸成本尤為顯著，這是由于每日需要收集的垃圾箱減少，使得處理量和運輸距離獲得不同程度的減少，從而降低總成本。

表6 兩種收集模式下成本對比Table 6 Cost comparison under two collection modes單位：元

這也表明決策過程中兩個決策主體之間產生了一定沖突，但由于智能回收企業不僅需要考慮建設成本和運營成本，還需要權衡運輸成本來保證總成本最優，因此是下層企業的決策牽制了上層的決策行為。綜上所述，本文模型應用智能垃圾收集路徑方式，依據閾值篩選需要收集的智能垃圾箱，再求解回收路徑最優方案，能夠很大程度降低總成本，減少資源浪費。

5.3 算法性能分析

為驗證提出的改進GA 算法對于求解帶容量約束的雙層選址路徑模型的性能，將GA-pro 求得的最優結果與標準遺傳算法（GA）、粒子群算法（PSO）和GAPSO混合算法求解結果進行對比分析，每種算法的種群大小為50，最大迭代次數為800，運行算法30次，選擇其中最佳優化結果如表7 所示，算法迭代效果對比如圖5 所示。基于這些圖表，從收斂速度、求解精度以及運算復雜度三個方面對算法性能進行對比分析。

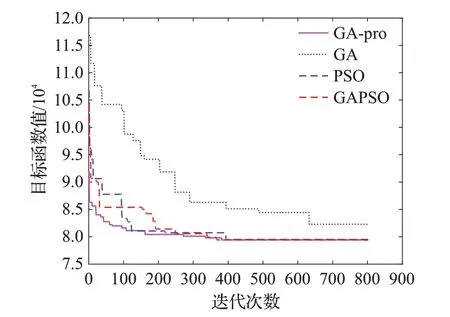
圖5 算法迭代對比圖Fig.5 Comparison for convergence curves

表7 四種算法最優結果對比Table 7 Optimal results for four algorithms

（1）觀察圖5可以看出，GA-pro收斂速度最快，PSO次之，標準GA收斂速度最慢。GA-pro算法于100代左右已收斂到最優值附近，在390代左右逐漸收斂于最優值；而PSO于120代左右開始收斂于最優值附近，在400代左右才逐漸收斂于最優值；GAPSO 雖然較早收斂于最優值，但其收斂速度較慢。

相比于標準GA 算法，GA-pro 迭代速度更快，最優解更佳，這是由于最優成本路線交叉算子能夠在確保容量約束的前提下將基因插入到局部最優位置，盡量避免非可行解產生的同時獲得更優的子代，反向變異算子反轉兩個隨機點位間所有基因可增加種群多樣性，有效提升算法的搜索性能，且精英選擇策略確保優良個體能傳遞至下一代，故GA-pro收斂性能遠優于標準遺傳算法。

（2）由表7 可知，四種算法都可以得到各自最優結果。GA-pro 算法求解結果比標準GA 算法優化了3.58%，比PSO 算法優化了0.08%，與GAPSO 最優解差距僅為0.05%。可見GA-pro 算法求解精度明顯高于標準遺傳算法，且相比于結果最優的GAPSO 混合算法差距不大。

（3）在算法復雜度方面，由于遺傳算法的復雜度可由適應度函數被調用的次數得出，而適應度函數的調用次數與種群數量、種群迭代次數、交叉率以及變異率相關[29]。以上變量均為外生給定，且GA-pro 僅在標準遺傳算法基礎上進行改進，沒有增加額外的復雜操作，故而在算法復雜度并沒有改變。

由上述對比分析可知，GA-pro 采用多種初始化方法，引入最優成本路線交叉算子、反向變異算子和精英選擇策略沒有增加算法復雜度的同時提高了搜索性能。綜上，GA-pro 對于求解智能垃圾回收下帶容量約束的雙層選址路徑問題是可行且有效的。

5.4 模型分析

為進一步驗證雙商品流選址-路徑模型的有效性，將結果與傳統選址-路徑模型的求解結果進行對比，如表8所示。采用相同數據的情況下，雙商品流選址-路徑模型在最優目標函數值和計算時間方面都較傳統模型有所提升。相比于使用GA-pro求解傳統模型，表7中標準GA 求解雙商品流選址-路徑模型的結果優化了1.66%，計算時間也減少了17.71%，這表明僅使用標準GA 求解引入雙商品流公式的選址-路徑模型也能求得良好的結果。

表8 模型結果對比Table 8 Comparison of model results

6 結論

本文研究智能垃圾回收下容量有限的雙層選址-路徑整合優化問題。上層智能回收企業以總成本最小為目標做收集中心選址決策；下層外包物流公司以運輸相關成本最小為目標，依據回收閾值選定容量不足的智能垃圾箱進行路徑規劃。設計改進的遺傳算法進行求解，GA 算法改進如下：（1）運用多種方法生成初始種群，上層采用聚類算法處理選址初始化，下層采用隨機和節約里程算法生成初始車輛路徑；（2）結合精英選擇策略，保留優秀個體；（3）采用最優成本路線交叉算子和反向變異算子維持種群多樣性。

選取Prins 和Barreto 提出的經典LRP 基準案例，驗證GA-pro求解CLRP的能力。將GA-pro結果與GAPSO和BSA 兩種算法求解結果進行對比分析，結果表明，GA-pro 在求解小規模問題時都能找到最優解，對于中大規模問題能求得近似最優解，整體求得結果與最優解的差距Gap均值分別為0.42%和1.63%，表現介于兩種對比算法之間，且Prins 算例的大規模算例中有三個案例的求解結果優于另兩個算法。此外，為探究本文模型與算法的適用性，基于模擬數據進一步測試。最終結果表明：（1）智能垃圾收集路徑方式，即先依據閾值確定亟待收集的垃圾箱再對其規劃回收路徑可有效降低成本，減少資源浪費；（2）GA-pro與其他三種算法的收斂性對比顯示，GA-pro 具有更優良的初始解，降低運行時間，具備良好的收斂性能；（3）引入雙商品流公式的選址-路徑模型在求解性能方面明顯優于傳統的選址-路徑模型。

綜上，本文可為智能垃圾回收下有容量限制的垃圾收集中心選址和路徑規劃問題提供決策支持。考慮不同決策主體間的復雜關系，引入雙商品流公式建立雙層選址-路徑模型，改進遺傳算法進行求解，并驗證智能垃圾收集路徑方式能夠有效降低回收成本，對規劃智能垃圾回收選址-路徑方案具有一定的參考意義。但是也存在一定的局限性，沒有考慮環境影響和多車型混合回收問題，這些將是下一步的研究方向。