非厄米Su-Schrieffer-Heeger鏈邊緣態和趨膚效應依賴的電子輸運特性*

楊艷麗 段志磊 薛海斌?

1) (晉中信息學院數理教學部,晉中 030800)

2) (太原理工大學物理學院,太原 030024)

1 引言

非厄米概念和拓撲思想之間的協同效應,即非厄米系統的拓撲性質是近年來一個非常活躍的研究領域[1-5].特別是,在非厄米系統中發現了許多厄米系統無對應的特殊拓撲性質.例如,在非厄米拓撲相中普遍存在的特殊點[2,4-8]、超越通常體邊對應關系[9-16]的缺陷邊緣態[14,15],以及非厄米系統在開邊界情形下本征態以指數衰減形式定域在其邊界附近的非厄米趨膚效應[3,17-31].其中,非厄米趨膚效應定義了非布洛赫的體邊對應關系,并建立了基于廣義布里淵區的非布洛赫能帶理論.因而,非厄米Su-Schrieffer-Heeger (SSH)鏈[32]的非厄米趨膚效應引起人們極大的研究興趣,并且該特性已經在拓撲電路[9]、光子晶格[10,19,23]、力學超材料[11]、光波導[17]、光子晶體[18]、冷原子[21]、聲子晶體[22]中觀察到.雖然在經典和量子模擬器中實驗設計非厄米模型取得了巨大進展,但是在實驗和理論上如何探測非厄米SSH鏈的缺陷邊緣態仍然是非厄米物理學的重要課題之一.例如,在一個耗散Aharonov-Bohm鏈中,態的邊界動力學特性可以用來探測其非平庸拓撲邊緣態[33].最近,在厄米SSH鏈系統中,利用電子在零能附近透射率峰個數隨著其與源極、漏極之間隧穿耦合強度的變化可以用來判斷該系統是否具有非平庸拓撲態[34-36].但是,如何基于電子輸運特性探測非厄米SSH鏈的缺陷邊緣態仍然是一個開放的課題.特別是,非厄米SSH鏈的非平庸拓撲邊緣態對其非厄米趨膚效應的影響尚未被揭示.

本文將研究非厄米SSH鏈非平庸拓撲邊緣態和趨膚效應依賴的電子輸運性質,并探尋如何基于電子輸運特性探測其非平庸拓撲邊緣態和趨膚效應.研究發現,電子在零能附近透射率峰的峰值是否遠小于或者遠大于1,可以用來判斷非厄米SSH鏈是左趨膚效應還是右趨膚效應,并且非厄米趨膚效應在非平庸拓撲邊緣態區域內被進一步增強.另外,非厄米SSH鏈的非平庸拓撲邊緣態可以通過逐漸改變其與源極、漏極之間的電子隧穿耦合強度,觀察電子在零能附近反射率谷的數目變化來判斷.

2 理論模型與研究方法

2.1 耦合導線的非厄米SSH鏈

一般情形下,一維SSH鏈系統的非厄米性通過格點上的增益/損耗平衡和兩個格點之間的不對稱定向跳躍這兩種方式進行設計[1-3].在本文中,考慮后一種設計方案,即兩個格點之間的非互易跳躍,如圖1所示,則在緊束縛近似下非厄米SSH鏈的哈密頓量可表示為[13-15,32,37]

圖1 非厄米SSH鏈與左、右導線耦合系統的示意圖,其中,小的實心圓(紅色)表示A子格,大的實心圓(綠色)表示B子格,空心圓(黑色)表示導線上的原子Fig.1.Schematic diagram of the non-Hermitian SSH chain coupled to the left and right leads.The small solid circles (red) represent the A sublattices,the large solid circles (green) represent the B sublattices,the hollow circles (black) represent atoms on the leads.

當非厄米SSH鏈與左、右導線耦合時,左、右電極的哈密頓量和其相應的電子隧穿耦合哈密頓量可以表示為

2.2 電子的反射率和透射率

為計算電子通過非厄米SSH鏈的反射率和透射率,假設電子從左導線(源極)入射.利用每個子格(原子)的瓦尼爾態,將與左、右導線耦合的非厄米SSH鏈的波函數 |ψ〉寫為[34-36]

其中,|α,j〉表示α導線上第j個原子的瓦尼爾態,aα,j,k則表示相應的瓦尼爾態 |α,j〉的概率幅;|n,β〉表示非厄米SSH鏈第n個原胞內β子格(β=A,B)的瓦尼爾態,dn,β,k則表示相應的瓦尼爾態|n,β〉的概率幅,k為入射電子的波矢.將與左、右導線耦合的非厄米SSH鏈的哈密頓量(5)式和其波函數(6)式代入定態薛定諤方程H|ψ〉=E|ψ〉,這里E=2t0cos(ka) 表示入射電子的能量,a為相應的晶格常數,由方程兩邊同一瓦尼爾態的系數相等并利用傳輸矩陣方法可得

其中:

為方便計算電子的反射率和透射率,將晶格常數a和導線上相鄰原子之間的跳躍振幅t0取為 1,并將左、右導線上第j個原子的概率幅展成平面波的形式:

其中,r和t分別表示電子的反射和透射振幅.將(14)式代入(7)—(9)式中,并將r,d1,A,k,dN,B,k,t看成4個未知數,相應地,可以求解出r和t的數值.因而,電子的反射率和透射率可以分別表示為R=|r|2和T=|t|2.

3 結果與討論

3.1 非厄米SSH鏈的邊緣態和纏繞數

對于非厄米SSH鏈,在動量空間中,其哈密頓量(1)式在周期性邊界條件下可以表示為

其 中,ψk=(dA,k,dB,k)T,HNH,SSH(k) 是一個非對角矩陣:

由圖2可知,在非厄米SSH鏈的非平庸拓撲相變區域內,其能量本征值為實數,如圖2(a1),(b1)以及圖2(a2),(b2)所示.因此,可以通過相似變換來求解其非平庸拓撲相變點[14,15,37].首先,將非厄米SSH鏈的波函數寫為

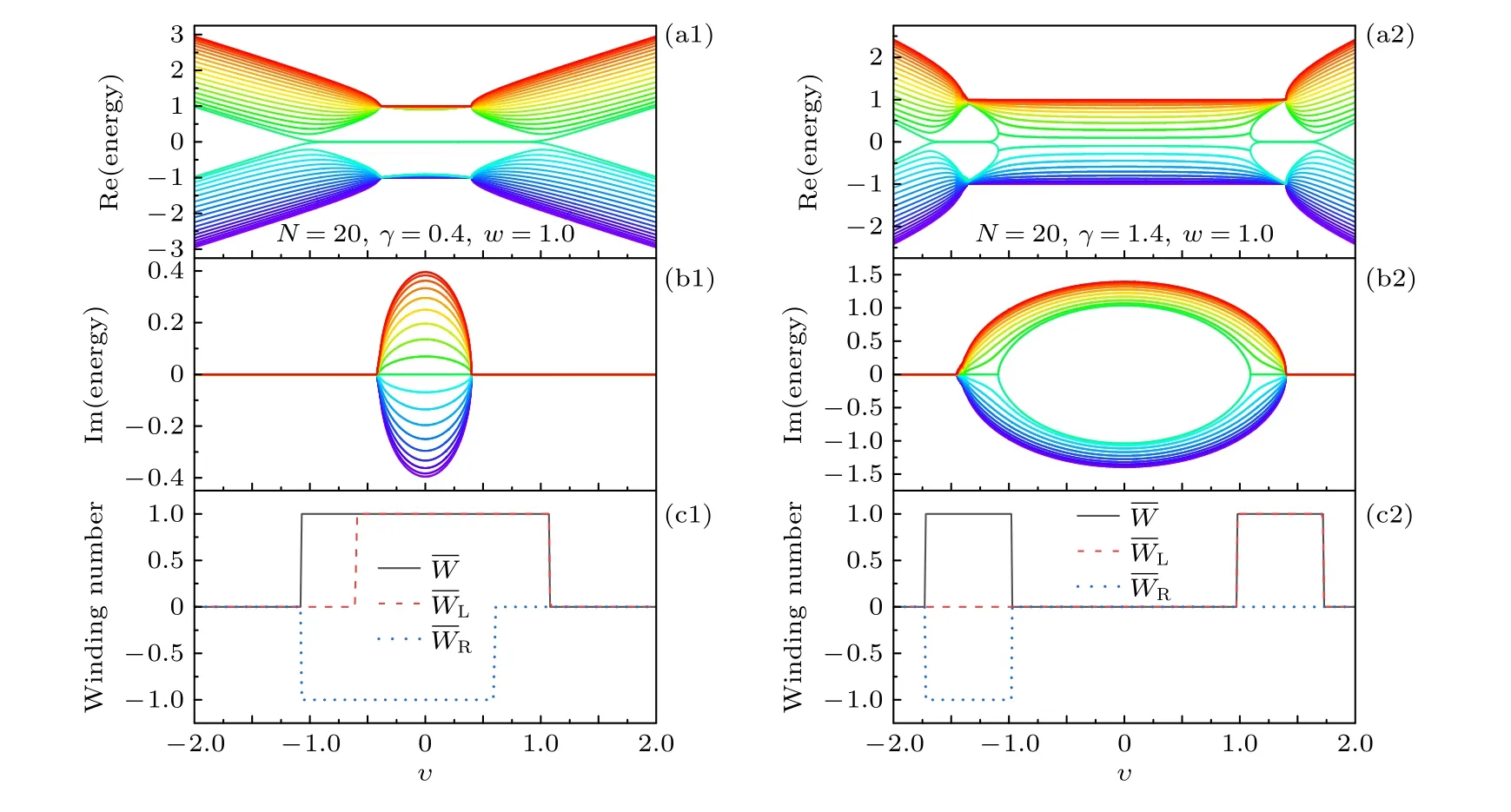
圖2 (a1),(a2)非厄米SSH鏈的能譜圖實部;(b1),(b2)非厄米SSH鏈的能譜圖虛部;(c1),(c2)非厄米SSH鏈的不同纏繞數隨著 υ 的變化圖.其中,(a1),(b1),(c1) γ=0.4;(a2),(b2)和(c2) γ=1.4.非厄米SSH鏈的其他參數選取為 w=1.0,N=20Fig.2.(a1),(a2) Real part of the energy spectrum of the non-Hermitian SSH chain;(b1),(b2) imaginary part of the energy spectrum of the non-Hermitian SSH chain;(c1),(c2) the different winding number of the non-Hermitian SSH chain as a function of the value of υ.Here,(a1),(b1),(c1) γ=0.4;(a2),(b2),(c2) γ=1.4.The other parameters of the non-Hermitian SSH chain are chosen as w=1.0 and N=20.

在實空間中,本征方程HNH-SSH|Ψ〉NH-SSH=ENH-SSH|Ψ〉NH-SSH等價于

為了研究非厄米SSH鏈的非平庸拓撲邊緣態性質,本文采用邊緣態依賴的纏繞數描述該性質,其中,左、右邊緣態的纏繞數分別定義為和.這里,WL和WR為布洛赫纏繞數,其定義為[14,15]

式中,hfor=υ-γ+weik是(16)式中向前跳躍的項,而hback=υ+γ+we-ik則是(16)式中向后跳躍的項;為非布洛赫纏繞數:

分γ＜w和γ＞w兩種情況,討論υ的取值對非厄米SSH鏈非平庸拓撲邊緣態性質的影響.為方便討論,在本文中,將胞間電子的跳躍振幅選取為能量單位,即w=1.0,非厄米SSH鏈的元胞數選取為N=20.當γ＜w時,這里選取γ=0.4,在非平庸拓撲相區域,如圖2(c1)中的區域,存在3種不同類型的邊緣態: 僅存在左邊緣態、僅存在右邊緣態,以及左、右邊緣態均存在,即其波函數的概率幅從非厄米SSH鏈的左端(左邊緣態)或右端(右邊緣態)或兩端(左、右邊緣態)向中間的子格位置快速衰減.為進一步研究υ的取值對零能左、右邊緣態的影響,圖3給出了零能附近的本征值的本征態波函數概率幅的絕對值隨子格n和υ值變化的相圖.當υ＞0 且其值趨于0時,非厄米SSH鏈的左、右邊緣態均存在,即其概率幅從左、右兩端的子格向中間的子格以指數形式快速衰減,其中,左邊緣態概率幅的絕對值大于其右邊緣態;反之,非厄米SSH鏈在υ＜0,且其值趨于0的情形下右邊緣態概率幅的絕對值大于其左邊緣態,如圖3(a)所示.當υ的絕對值 |υ| 較大時,對于υ＞0的情形,左邊緣態概率幅的絕對值大于其右邊緣態約5個量級,此時,右邊緣態將非常不明顯;而當υ＜0 時,右邊緣態概率幅的絕對值則大于其左邊緣態約5個量級,相應地,左邊緣態將非常不明顯,如圖3(a)所示.此特性是由于非厄米SSH鏈的趨膚效應引起,將在3.2節討論.另外,從圖3(a)還可以看出,當υ的值接近拓撲相變點時,非厄米SSH鏈在υ＞0 情形下將僅存在左邊緣態,而在υ＜0 情形下將僅存在右邊緣態.對于γ＞w的情形,在非平庸拓撲邊緣態區域內,非厄米SSH鏈在υ＞0 情形下僅存在左邊緣態;而在υ＜0情形下則僅存在右邊緣態,如圖3(b)所示.此外,當υ=γ時,在非厄米SSH鏈的第1個元胞內,電子從A子格到B子格的跳躍振幅為0,因而邊緣態的波函數概率幅將局域在非厄米SSH鏈最左端的子格上,即第1個子格上;而當υ=-γ時,在非厄米SSH鏈的最后一個元胞內,即第N個元胞內,電子從B子格到A子格的跳躍振幅為0,相應地,邊緣態的波函數概率幅則局域在非厄米SSH鏈最右端的子格上,第 2N個子格上.

圖3 非厄米SSH鏈在零能附近的本征值的本征態波函數概率幅的絕對值隨子格 n和υ 值變化的相圖 (a)γ=0.4;(b) γ=1.4;非厄米SSH鏈的其他參數選取為w=1.0,N=20Fig.3.Absolute value of probability amplitudes of the wave functions of the nearly zero-energy eigenstates of the non-Hermitian SSH chain as a function of the sublattice n and the value of υ : (a) γ=0.4;(b) γ=1.4.The other parameters of the non-Hermitian SSH chain are chosen as w=1.0 and N=20.

3.2 非厄米SSH鏈的趨膚效應和異常透射率

在非厄米SSH鏈中,趨膚效應和電子透射率異常是其區別于厄米SSH鏈的兩個重要物理現象.這里需要指出的是,與非厄米SSH鏈的非平庸拓撲邊緣態不同的是,趨膚效應是非厄米SSH鏈的所有本征態(包含邊緣態)波函數在每個子格上的概率分布均向其一端的子格上集中.首先研究υ的數值對非厄米SSH鏈趨膚效應的影響.

當γ＜w時,例如γ=0.4,對于一個有限長的非厄米SSH鏈,在υ值較小(υ=±0.01)的情形下,其未出現非厄米趨膚效應,如圖4(a1)和圖4(a2)所示;而僅當 |υ| 大于某一數值時,才能觀察到非厄米趨膚效應,如圖4所示.另外,由圖4可知,非厄米SSH鏈在左、右邊緣態區域(υ=0.2)和左邊緣態區域(υ=0.7)內均存在明顯的趨膚效應,如圖4(b1),(b2)以及圖4(d1),(d2)所示.尤其是,當υ=±γ時,非厄米SSH鏈的趨膚效應達到最強,對于υ=γ的情形,其本征態波函數的概率幅僅集中在最左端的3個子格上,如圖4(c1)所示;而對于υ=-γ的情形,其本征態波函數的概率幅則僅集中在最右端的3個子格上,如圖4(c2)所示.這里,特別需要說明的是,由于υ是厄米參數,繼續增大其絕對值會減弱系統非互易跳躍的不對稱性,從而減弱其非厄米趨膚效應,如圖4(e1)和圖4(e2)所示.特別是,當υ的絕對值足夠大時,對于一個有限長的非厄米SSH鏈,其趨膚效應將消失.

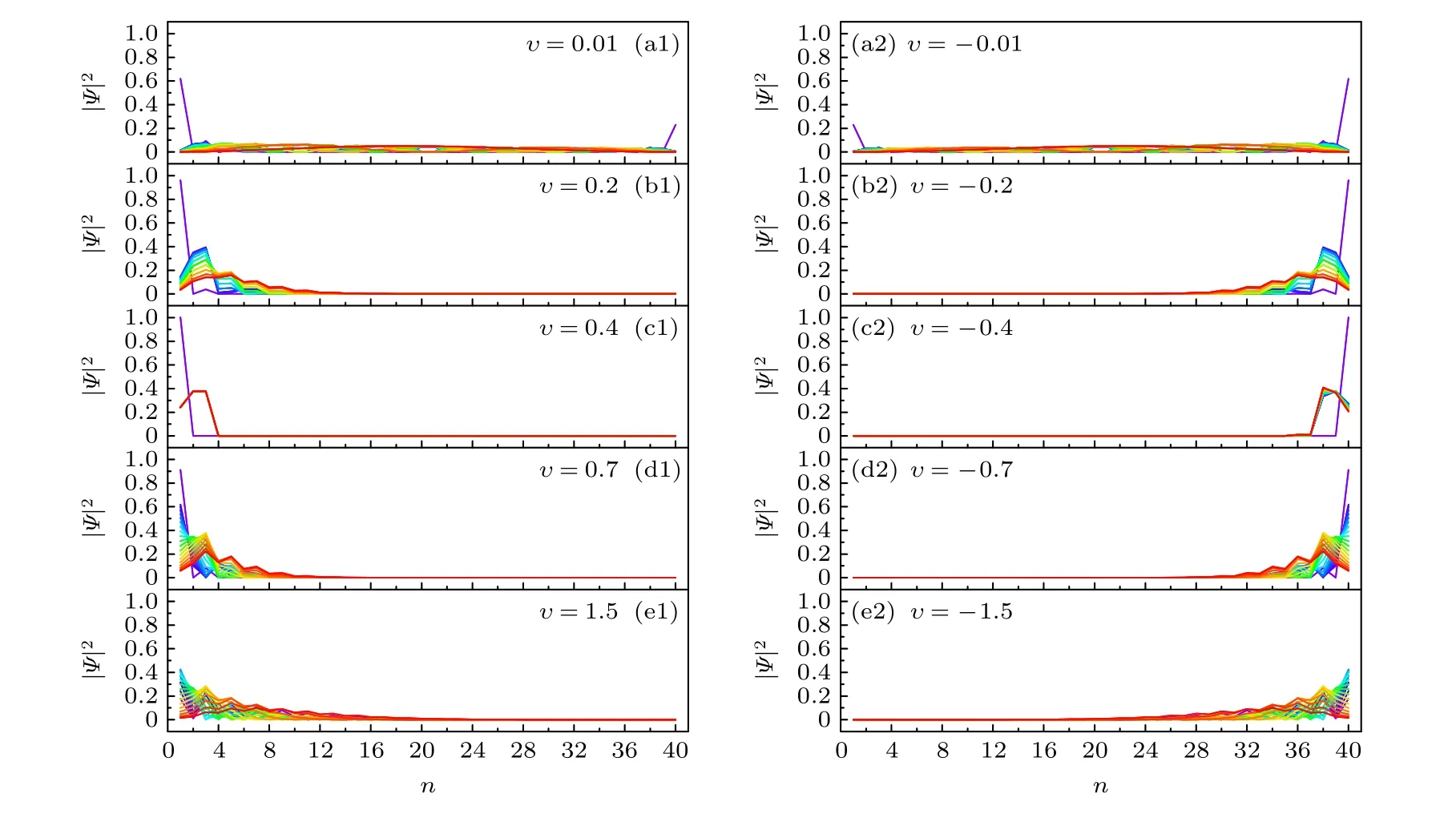
圖4 非厄米SSH鏈的本征態波函數在每個子格上的概率分布圖 (a1) υ=0.01;(a2) υ=-0.01;(b1) υ=0.2;(b2) υ=-0.2;(c1) υ=0.4;(c2) υ=-0.4;(d1) υ=0.7;(d2) υ=-0.7;(e1) υ=1.5;(e2) υ=-1.5;非厄米SSH鏈的其他參數選取為γ=0.4,w=1.0,N=20Fig.4.Distribution of probabilities of the wave functions of the non-Hermitian SSH chain: (a1) υ=0.01;(a2) υ=-0.01;(b1) υ=0.2;(b2) υ=-0.2;(c1) υ=0.4;(c2) υ=-0.4;(d1) υ=0.7;(d2) υ=-0.7;(e1) υ=1.5;(e2) υ=-1.5.The other parameters of the non-Hermitian SSH chain are chosen as γ=0.4,w=1.0 and N=20.

對于γ＞w的情形,例如γ=1.4,非厄米SSH鏈的左趨膚效應在其左邊緣態區域內(例如υ=1.3和υ=1.5),比其在非邊緣態區域內(例如υ=0.5和υ=2.0)更加明顯,如圖5(a1),(b1),(d1),(e1)所示.相應地,非厄米SSH鏈的右趨膚效應在其右邊緣態區域內(例如υ=-1.3和υ=-1.5),比其在非邊緣態區域內(例如υ=-0.5和υ=-2.0)更加明顯,如圖5(a2),(b2),(d2),(e2)所示.同樣,當υ=±γ時,非厄米SSH鏈的趨膚效應達到最強,如圖5(c1),(c2)所示.

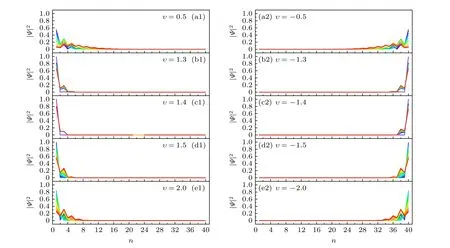
圖5 非厄米SSH鏈的本征態波函數在每個子格上的概率分布圖 (a1) υ=0.5;(a2) υ=-0.5;(b1) υ=1.3;(b2) υ=-1.3;(c1) υ=1.4;(c2) υ=-1.4;(d1) υ=1.5;(d2) υ=-1.5;(e1) υ=2.0;(e2) υ=-2.0;非厄米SSH鏈的其他參數選取為γ=1.4,w=1.0,N=20Fig.5.Distribution of probabilities of the wave functions of the non-Hermitian SSH chain: (a1) υ=0.5;(a2) υ=-0.5;(b1) υ=1.3;(b2) υ=-1.3;(c1) υ=1.4;(c2) υ=-1.4;(d1) υ=1.5;(d2) υ=-1.5;(e1) υ=2.0;(e2) υ=-2.0.The other parameters of the non-Hermitian SSH chain are chosen as γ=1.4,w=1.0 and N=20.

其次,研究υ的數值對非厄米SSH鏈電子透射率的影響.在非厄米SSH鏈中,由于電子從左電極(源極)到右電極(漏極)的向前跳躍振幅不等于從右電極(漏極)到左電極(源極)的向后跳躍振幅,因而,其電子透射率的數值將不等于1.為了方便討論電子透射率異常的情況,這里將胞內電子從A子格到B子格的跳躍振幅 (υ-γ) 和其從B子格到A子格的跳躍振幅 (υ+γ) 分別重新寫為[13].相應地,電子通過非厄米SSH鏈的歸一化透射率可以表示為TN=T/|e?|2N,相應地,歸一化透射率TN的最大值為1.

對于厄米SSH鏈的零能非平庸拓撲邊緣態,可以通過其零能附近的電子透射率來探測[34-36],而非厄米SSH鏈的趨膚效應又與其電子透射率的異常相關,因而,非厄米SSH鏈的電子輸運特性為探測其邊緣態和趨膚效應提供了一個可選擇的思路,即從電子輸運的角度,討論如何探測非厄米SSH鏈的邊緣態和趨膚效應.

3.3 非厄米SSH鏈邊緣態和趨膚效應的探測

對于本文考慮的有限長的非厄米SSH鏈,兩個非平庸拓撲邊緣態的能量本征值之差實際上并不為零.因此,當非厄米SSH鏈與左、右導線之間的電子隧穿振幅處于弱耦合區域時,非厄米SSH鏈與導線之間的弱電子隧穿過程對其能級結構影響較小.因而,在零能附近電子透射率峰/反射率谷的能量位置可以反映相應邊緣態的能級位置.但是,當非厄米SSH鏈與左、右導線之間的隧穿振幅處于強耦合區域時,導線與非厄米SSH鏈之間的強電子隧穿過程會強烈地影響非厄米SSH鏈的能級結構.此時,非厄米SSH鏈在零能附近無能級,相應地,弱耦合情形觀察到的電子透射率峰/反射率谷將在強耦合情形下消失.另一方面,由3.2節可知,非厄米SSH鏈的趨膚效應與其電子透射率的異常相關.因此,這里選取非厄米SSH鏈與左、右導線之間的電子隧穿耦合振幅tL和tR為可調的物理變量,研究與非厄米SSH鏈邊緣態和趨膚效應相關聯的電子透射率和反射率特性.

首先,討論在γ＜w情形下非厄米SSH鏈與左、右導線耦合的情況,例如,γ=0.4.當非厄米SSH鏈與左、右導線弱耦合時,即tL=tR的數值較小時,對于υ＞0 的情形,非厄米SSH鏈的左趨膚效應體現在其本征態波函數在每個子格上的概率幅更加集中在其左端的幾個子格上.相應地,電子從左電極隧穿到非厄米SSH鏈,再從非厄米SSH鏈隧穿出到達右電極的概率將指數衰減.因此,在零能附近可以觀察到兩個峰值遠小于1的電子透射率峰,如圖6(a1)所示.反之,當υ＜0 時,非厄米SSH鏈的右趨膚效應則體現在其本征態波函數在每個子格上的概率幅更加集中在其右端的幾個子格上,相應地,電子從左電極隧穿到非厄米SSH鏈,再隧穿出非厄米SSH鏈到達右電極的概率將指數增大.因而,可以在零能附近觀察到兩個峰值遠大于1的電子透射率峰,如圖6(a2)所示.事實上,對于γ=0.4和υ=0.5的情形,其歸一化透射率因子為||e?||=1/3＜1,相應的透射率T?1;而對于γ=0.4和υ=-0.5的情形,相應的歸一化透射率因子為||e?||=3＞1,因而,其透射率T?1.因此,對于非厄米SSH鏈的趨膚效應類型,可以通過其電子透射率是否遠大于或者遠小于1來判斷.例如,當電子透射率遠小于1時,對應于左趨膚效應;而電子透射率遠大于1,則對應于右趨膚效應.

圖6 非厄米SSH鏈的電子透射率和反射率隨不同隧穿耦合振幅和入射電子能量變化的相圖 (a1),(b1) υ=0.5;(a2),(b2) υ=-0.5;非厄米SSH鏈的其他 參數選取為 γ=0.4,w=1.0,N=20Fig.6.Transmission probabilities and reflection probabilities of the non-Hermitian SSH chain as a function of the amplitude of tunneling coupling and the energy of incident electron: (a1),(b1) υ=0.5;(a2),(b2) υ=-0.5.The other parameters of the non-Hermitian SSH chain are chosen as γ=0.4,w=1.0 and N=20.

從圖6(a1)和圖6(a2)可以看出: 隨著非厄米SSH鏈與左、右導線的電子隧穿耦合振幅tL和tR的逐漸增大,在弱耦合情形下,零能附近兩個尖銳的透射率峰首先被逐漸展寬但其峰值不變;然后,這兩個尖銳的峰將逐漸合并為一個半寬較寬的峰值不變的透射率峰;當電子隧穿耦合振幅tL和tR繼續增大時,這個透射率峰的半寬將被繼續展寬,并且其峰值也將減小;最后,這個半寬很寬的電子透射率峰將完全消失.另外,對于非厄米SSH鏈,電子從左電極隧穿到非厄米SSH鏈后,其在胞內從A子格到B子格的跳躍振幅將被增強或衰減,相應的其在零能附近透射率峰的峰值也不再等于1.但是,對于在左電極(源極)和非厄米SSH鏈界面反射的電子,其在相鄰格點的隧穿振幅不會被增強或者衰減,因而,其在零能附近相應反射率谷的谷值可以等于0,如圖6(b1)和圖6(b2)所示.特別是,隨著電子隧穿耦合振幅tL和tR的逐漸增大,在零能附近反射率谷的數目變化與透射率峰的數目變化規律相同,如圖6(a1),(b1)以及圖6(a2),(b2)所示.因此,對于非厄米SSH鏈的非平庸拓撲邊緣態,可以通過調節非厄米SSH鏈與左、右導線之間的電子隧穿耦合振幅tL和tR,觀察電子在零能附近反射率谷的數目變化來確定其是否存在非平庸拓撲邊緣態.

對于γ＞w的情形,電子在零能附近的透射率和反射率隨著非厄米SSH鏈與左、右導線之間電子隧穿耦合振幅tL和tR變化的規律與γ＜w情形相同,但其tL和tR的取值不同,如圖7所示.下面,討論非厄米SSH鏈在零能附近電子輸運特性的物理機制.

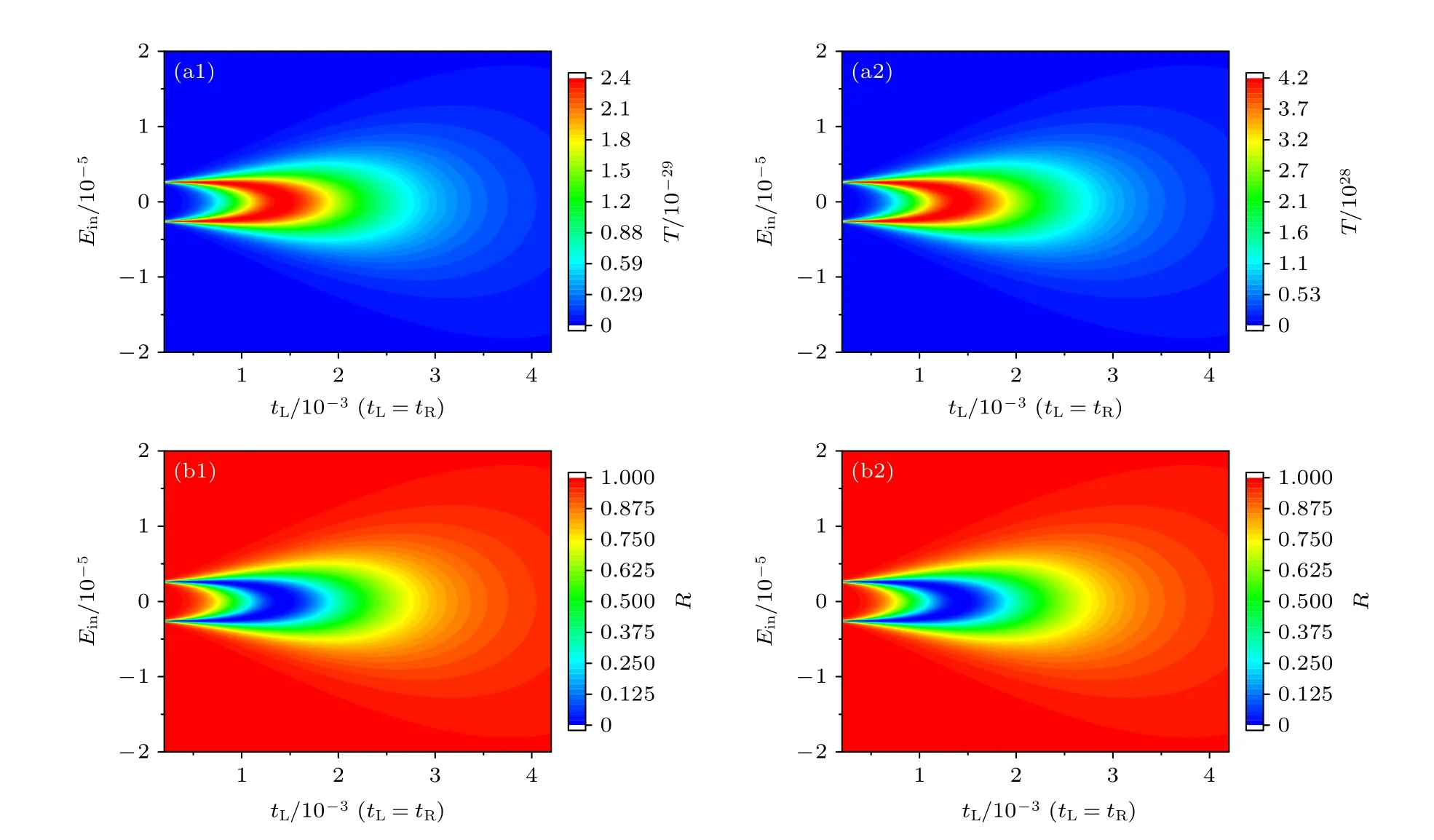
圖7 非厄米SSH鏈的電子透射率和反射率隨不同隧穿耦合振幅和入射電子能量變化的相圖 (a1),(b1) υ=1.3;(a2),(b2) υ=-1.3;非厄米SSH鏈的其他 參數選取為 γ=1.4,w=1.0,N=20Fig.7.Transmission probabilities and reflection probabilities of the non-Hermitian SSH chain as a function of the amplitude of tunneling coupling and the energy of incident electron: (a1),(b1) υ=1.3;(a2),(b2) υ=-1.3.The other parameters of the non-Hermitian SSH chain are chosen as γ=1.4,w=1.0 and N=20.

當非厄米SSH鏈與左、右導線耦合時,其能級結構將受到非厄米SSH鏈與左、右導線之間電子隧穿耦合振幅tL和tR數值大小的影響.當tL和tR數值很小時,電子在非厄米SSH鏈與導線之間的隧穿過程被強烈壓制.此時,電子隧穿過程對非厄米SSH鏈的能級結構影響較小.相應地,零能附近邊緣態反射率谷對應的能量位置與非厄米SSH鏈的能級一一對應,如圖8(a1)和圖8(b1)所示.若繼續增大tL和tR的數值使其到達某一值時,非厄米SSH鏈的能級結構將受到其與左、右導線之間電子隧穿過程的強烈影響.這里將左、右導線分別用瓦尼爾態 |L〉和|R〉表示,再通過研究非厄米SSH鏈與瓦尼爾態 |L〉和|R〉耦合的系統能譜,定性模擬非厄米SSH鏈在其與左、右導線強耦合情形下的能級結構.在左電極的瓦尼爾態 |L〉、非厄米SSH鏈子格的瓦尼爾態{|1,A〉,|1,B〉,···,|n,A〉,|n,B〉}、右電極的瓦尼爾態 |R〉組成的完備基下,由(5)式可知,上面系統哈密頓量的矩陣形式為將(25)式嚴格對角化可得上面的修正系統能譜.由圖8(a2)和圖8(b2)可知,當γ=0.4 和γ=1.4時,對于非厄米SSH鏈與左、右導線強耦合的情形,其在零能附近均沒有能級存在.因而,當tL和tR的數值增大到某一臨界值(大小依賴于γ和υ)時,在零能附近電子的反射率峰和透射率谷都將全部消失,如圖6和圖7所示.

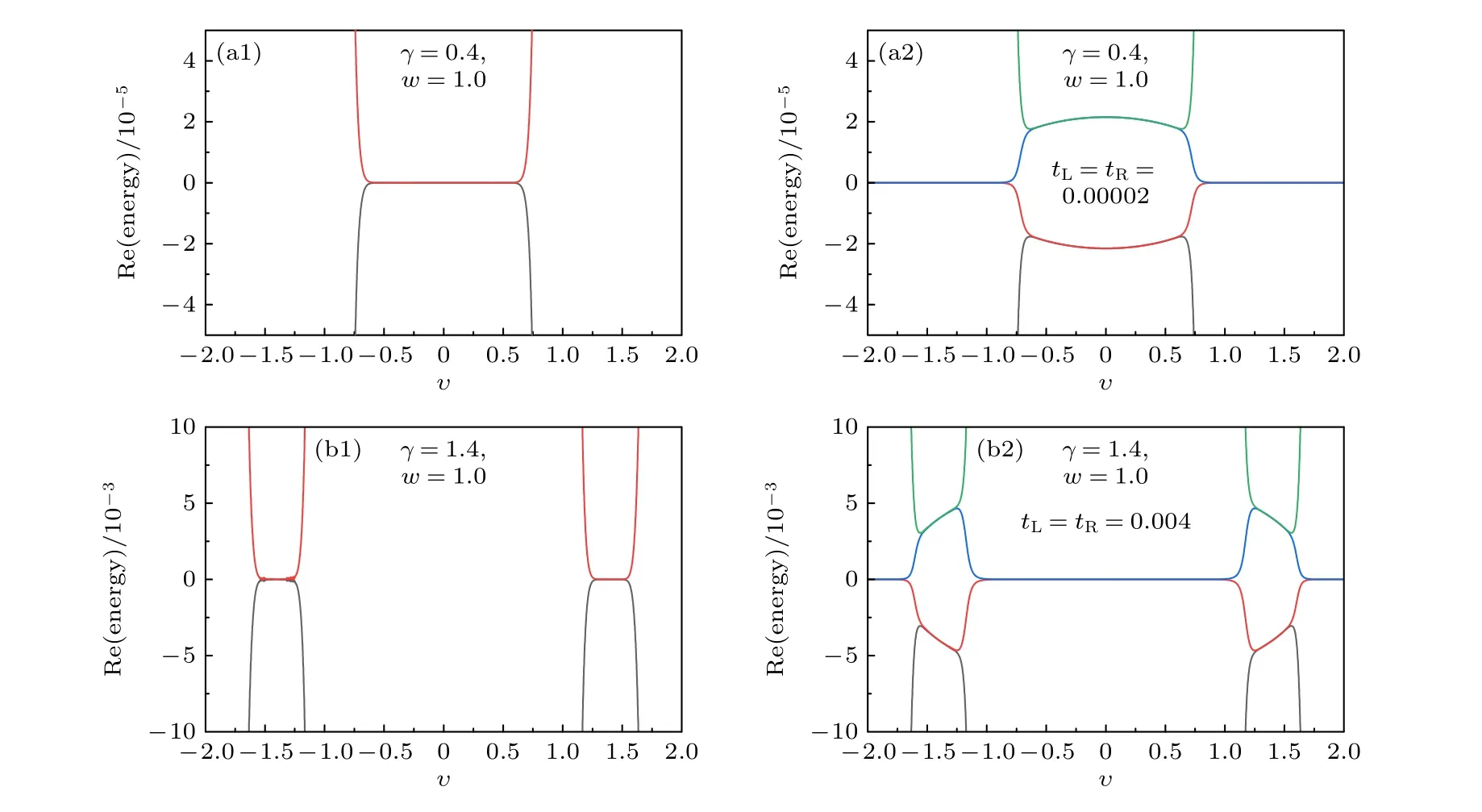
圖8 (a1),(b1)非厄米SSH鏈在零能級附近的能譜圖;(a2),(b2)非厄米SSH鏈與左導線原子 j=-1 和右導線原子 j=1 耦合的修正系統在零能級附近的能譜圖.其中,(a1) γ=0.4,(a2) γ=0.4,tL=tR=0.00002;(b1) γ=1.4,(b2) γ=1.4,tL=tR=0.004.非厄米SSH鏈 的其他參數選取為 w=1.0,N=20.Fig.8.(a1),(b1) Real part of the energy spectrum of the non-Hermitian SSH chain in thevicinity of the zero energy;(a2),(b2) real part of the energy spectrum of the non-Hermitian SSH chain coupled to the first sublattice of the left lead j=-1 and that of the right lead j=1 in the vicinity of the zero energy.Here,(a1) γ=0.4,(a2) γ=0.4,tL=tR=0.00002;(b1) γ=1.4,(b2)γ=1.4,tL=tR=0.004.The other parameters of the non-Hermitian SSH chain are chosen as w=1.0 and N=20.

對于非邊緣態區域,即非零能的情形,非厄米SSH鏈能量本征值(實部)最小的兩個本征態之間的能量本征值之差明顯大于0,如圖2(a1)和圖2(b1),因而,其在零能附近沒有能級,即對入射電子來說是禁帶,此時電子的透射率為零,相應的反射率為1.因此,當調節非厄米SSH鏈與左、右導線之間的電子隧穿耦合振幅,使其從弱耦合區域變化到強耦合區域,在非邊緣態的區域內,觀察不到電子的反射率谷及其反射率谷的數目變化.因此,對于非厄米SSH鏈是否存在邊緣態,可以通過調節非厄米SSH鏈與左、右導線之間的電子隧穿耦合振幅,使其從弱耦合區域變化到強耦合區域,然后觀察電子在零能附近電子反射率谷的數目在此過程中的變化來判斷邊緣態是否存在.例如,當電子在弱耦合情形下的2個零能附近反射率谷在強耦合情形下消失,則說明非厄米SSH鏈存在邊緣態.另外,對于非厄米SSH鏈的趨膚效應,可以通過其電子透射率是否遠小于1或遠大于1來判斷其趨膚效應的類型,即電子透射率遠小于1對應于左趨膚效應,而電子透射率遠大于1則對應于右趨膚效應.

4 結論

本文研究了非厄米SSH鏈的非平庸拓撲邊緣態性質和其趨膚效應,并基于零能附近的電子輸運特性給出了探測其邊緣態和趨膚效應類型的理論方案.研究發現,非厄米SSH鏈的趨膚效應類型與其電子在零能附近透射率峰的峰值密切相關,例如,當電子在零能附近透射率峰的峰值遠小于1時,非厄米SSH鏈具有左趨膚效應;反之,當電子在零能附近透射率峰的峰值遠大于1時,非厄米SSH鏈則具有右趨膚效應.特別是,在非平庸拓撲邊緣態區域內,非厄米SSH鏈的邊緣態將進一步增強其趨膚效應.另外,當非厄米SSH鏈與左、右導線之間的電子隧穿耦合振幅處于弱耦合區域時,在零能附近可以觀察到2個電子反射率谷;而在其強耦合區域時,電子在零能附近的反射率谷將消失.此特性可以用來探測非厄米SSH鏈的非平庸拓撲邊緣態.上述結果為探測非厄米SSH鏈的非平庸拓撲邊緣態和非厄米趨膚效應類型提供了一種可選擇的理論方案.