溝槽結構對水潤滑軸承潤滑特性影響機制?

汪 驥 于鵬法 李 瑞 劉玉君 劉 曉 高 立 李晨龍

（大連理工大學船舶工程學院 遼寧大連 116024）

船舶水潤滑軸承是一種節能環保的滑動軸承，水泵、船尾管和水輪發動機主軸等。與傳統滑動軸承不同的是，為了使進入開式水潤滑軸承的泥沙顆粒快速排出，減少泥沙對于摩擦副間的磨損，同時為了更快地排出軸承在工作過程中產生的熱量，需要在軸承內襯材料上開出溝槽結構。因此，溝槽結構對于水潤滑軸承尤其是大型水潤滑軸承來說不可或缺。

水潤滑軸承發展至今，已開發了許多結構的溝槽類型。按照溝槽結構相對于軸承的大小可分為深溝槽結構和微溝槽結構。研究表明，形成流體動壓潤滑后，深溝槽結構的水潤滑軸承其水膜壓力在溝槽處不連續，使得壓力在溝槽處降為表壓為0。微溝槽是指溝槽結構參數遠遠小于深溝槽的溝槽，對于微溝槽來說，其在微溝槽內部會形成流體動壓效應。

在微溝槽結構對水潤滑軸承潤滑性能影響的研究方面，學者們已經展開了大量的研究。SHINKARENKO等［1］研究了物體表面紋理對軟彈流潤滑性能的影響，指出微體之間的潤滑劑會產生額外的擠壓效應。GONG 等［2］建立了水潤滑微槽軸承的彈性流體動力潤滑（EHL）模型，并對模型進行了實驗驗證，研究了偏心率和軸承材料對微槽軸承潤滑性能的影響。XIE等［3］通過建立二維模型，詳細探討了操作條件和結構參數對流體特征的影響，研究了矩形微腔體內的潤滑機制及潤滑性能隨腔體結構的變化規律。SHI 等［4］建立了軸承彈流潤滑的數學模型，并根據載荷增量法和有限差分法分析了水潤滑橡膠軸承在小擾動條件下的動態特性。王家序等［5］對微溝槽形貌對水潤滑軸承混合潤滑特性的影響進行了研究，指出由于不同溝槽內水膜增壓能力以及抽吸作用的不同引起了水潤滑軸承混合潤滑性能的差異。GAO 等［6］利用計算流體動力學分析了不同軸承尺寸下、不同轉速下偏心率對水膜壓力分布的影響，為設計高效水潤滑滑動軸承的初始直徑尺寸的選擇提供了參考。TALA－ IGHIL 和FILLON［7］通過適當的表面紋理幾何形狀和軸承表面上正確的紋理分布，發現軸承性能的提高主要通過最小的膜厚度來實現，在一定程度上也是通過增加微觀特征來實現提高潤滑性能。解忠良、焦春曉等［8－9］從微觀層面探究粗糙峰與軸承潤滑狀態轉變之間的關系，進而提出判斷潤滑狀態轉變的微觀尺度標準。

對于深溝槽軸承，多位學者也深入探討了溝槽結構對軸承潤滑性能的影響［10－15］。楊利濤［16］通過建立圓弧型溝槽模型，分析了不同工況及軸承結構下的軸承潤滑性能，發現溝槽處水壓會出現降低的情況。王楠等人［17］利用有限元軟件，研究了考慮軸瓦變形后的八溝槽水潤滑橡膠軸承在不同偏心率和轉速下的水膜壓力分布，發現溝槽對水膜壓力影響較大。劉宇等人［18］對軸向開槽水潤滑徑向軸承的潤滑性能進行數值計算與分析，結果表明：軸向開槽軸承壓力分布不連續，水槽處壓力降低為0；軸承開槽后承載能力降低，槽的寬度越大，個數越多，軸承的承載能力越小。WANG 等［19］以實驗的方式揭示了全尺寸WSB 的壓力偏差和雙向軸傾斜現象，系統地研究了偏心率、軸傾角和軸承結構參數對潤滑和動態特性的影響，證實了溝槽結構對船用水潤滑艉軸承的運行性能有很大的影響。

基于以上研究內容可以發現，相比于深溝槽結構，水潤滑軸承的微溝槽結構可以提高軸承的承載能力和局部水壓，改善軸承的潤滑性能。然而，不同溝槽尺寸對水潤滑軸承潤滑特性的差異性影響，目前的研究還難以從原理上去解釋。因此，本文作者以簡化后的橢圓形溝槽為研究對象，提出了采用深深比（軸承間隙與溝槽深度的比值）、寬深比（溝槽寬度與溝槽深度的比值）等參數來表征水潤滑軸承的溝槽結構，通過數值仿真得到溝槽內部的壓力輪廓，研究了結構參數對水潤滑軸承溝槽內部流體流動特征的影響，分析了溝槽結構參數對水潤滑軸承摩擦因數的影響和軸承的潤滑機制。文中通過CFD 方法從微觀和宏觀層面揭示溝槽結構對船用水潤滑軸承潤滑特性影響機制，為水潤滑軸承優化設計提供了參考。

1 分析模型

1.1 流體動力學的控制方程

1.1.1 連續性方程

在水潤滑軸承中，軸承內液體的流動遵循質量守恒定律，即在單位時間里流入微元的凈質量，等于微元體內質量的增加率。對其內部的流體作連續性假設，假定微溝槽內的流體是不可壓縮的、等熱和等黏流體，滿足Navier－Stokes（N－S）方程的要求。由此可推導出連續性方程（即質量守恒方程）的微分表達式為

式中：ρ是密度；t是時間；ux、uy、uz是速度矢量u的x、y、z分量。

式（3）即為水潤滑軸承適用的連續性方程。

1.1.2 動量守恒方程

動量守恒定律表現為在單位時間里，作用于微元體上的各外力之和，等于流體動量的變化率。由此可導出動量守恒方程，即運動方程，又稱作N－S 方程，完整形式如下所示：

式中：Fi是微元體上的重力等體力；p是流體微元體上的壓力；τii、τij（i，j＝x、y、z）是微元體表面上黏性應力的分量。

對牛頓流體，有如下關系式：

式中：λ為第二黏度，取λ＝－2／3；μ為動力黏度。

將式（5）代入式（4），得到動量守恒方程：

式中：Si（i＝x、y、z）為方程的廣義源項；grad（ui）＝?ui／?x＋?ui／?y＋?ui／?z（i＝1、2、3）。

1.2 流動狀態

軸承在運轉過程中尤其是在高速旋轉過程中，其內部液體很容易進入湍流狀態。對于水潤滑軸承，由于水的黏度較低，很容易使流體的流動狀態由層流變為湍流。判斷流體流動狀態通常用特征量雷諾數Re表征。對于水潤滑軸承，雷諾數定義為以下公式：

式中：ρ是流體密度；v是表面線速度；A是過流斷面截面積；η是流體的動力黏度；x是固體與流體在過流斷面上接觸的濕周長。

通常認為當雷諾數超過臨界雷諾數時，流體流動狀態便由層流狀態變為湍流狀態。對于水潤滑軸承，出現湍流的臨界雷諾數Rec為

式中：R為軸頸半徑；c為軸承間隙。

1.3 空化模型

由于水的汽化壓力很低，恒定溫度下，液體壓力降至低于飽和蒸汽壓時，液體破裂，或溶有的微小空氣泡、氣核，在降壓下長大且形成氣穴，產生空化現象，其實質是氣液兩相之間的傳質相變。在水潤滑系統中很容易產生空化現象。空化過程中液相與氣相的質量傳遞由以下方程控制：

式中：αv為氣相體積分數；ρv為氣體密度；Rg和Rc表示空化過程中液相和氣相之間的質量傳遞。

1.4 軸承摩擦因數

依據以上方程可以求得軸承內水膜的壓力分布，對壓力進行積分可以得到軸承在x和y方向上的承載力Fe和Fθ為

水潤滑軸承總的承載力為

假設橡膠軸瓦內表面的摩擦力全部由流體內部的黏性剪切流引起，對水潤滑軸承進行數值模擬。沿軸頸圓周方向，對流體的黏性剪切力求積分，得到摩擦力，其計算式如下：

摩擦因數計算式為

2 模型和邊界條件

2.1 模型簡化

圖1 顯示了文中計算的模型簡化過程。在最終構建完成的簡化模型中，壓力進出口模擬軸承在溝槽部位的入水和出水，靜止壁面模擬軸承內襯部分，采用滑移壁面來模擬軸的轉動。構建局部溝槽有限元分析模型的目的是能更好地顯示溝槽內部流體的流動狀態，分析其內部流動和潤滑演變過程。

橢圓形溝槽是船舶水潤滑軸承結構中最為常見的類型，其結構簡單易加工成型，且過渡均勻，可以改善溝槽的結構應力，因此文中選擇橢圓形溝槽作為研究對象。簡化后的分析模型結構參數如圖2 所示，其中l為所取模型的長度，c為軸承間隙，它是軸承表面與軸頸表面之間的距離；a、d分別為溝槽的寬度和深度。基于上述的模型簡化假設，為探討橢圓形溝槽的幾何參數對溝槽內部流動特征的影響，文中提出了采用如下參數來表征水潤滑軸承的溝槽結構：

式中：h1為深深比，指軸承間隙與溝槽的深度的比值；h2為寬深比，指溝槽寬度與溝槽深度的比值。

2.2 網格劃分及尺寸無關性驗證

采用有限元法進行分析計算時，網格單元質量和數量越高，其求解計算的精度也越高，但卻增加了求解計算的時間。為了減小網格數量和提高求解精度，文中分析計算的網格采用了高階單元和雙精度仿真。

圖1 展示了簡化后模型的部分網格局部放大圖。其中所有單元均為結構化網格，網格單元中無T 形邊和自由邊，在影響網格質量的因素中主要為單元質量和縱橫比，所對應的最優網格質量數值均為1。在文中對應的數值分別為0.964、1.09，說明該網格為高質量的網格，這對計算結果的精度是有益的。

如圖3 所示，經對不同數量及不同尺寸的網格進行分析，當流體域網格數量達到39 360，網格尺寸為0.005 mm 時溝槽內部最大壓力保持穩定，滿足計算要求。

圖3 網格尺寸無關性驗證Fig.3 Mesh－independent size verification

2.3 CFD 前處理

求解過程中假設流體是理想流體，并考慮了液體空化問題；求解使用簡化的多相流模型，即Mixture模型，第一相是水相，第二相是水蒸汽相；空化模型為Zwart－Gerber－Belamri 模型，氣相與液相間無相對滑移速度，忽略黏度與表面張力，空化壓力為2 340 Pa（絕對壓力），蒸發系數50，冷凝系數0.01，氣泡直徑0.001 mm，成核部位體積分數0.000 5。文中數值求解基于壓力求解器，假定潤滑狀態為水浴潤滑狀態。

求解方法選用了基于壓力－速度耦合的SIMPLEC算法，動量方程采用二階迎風離散格式進行離散，體積分數方程采用QUICK 離散格式。添加y方向上的力監測，當殘差達到所允許的殘差或y方向上的升力達到穩定狀態時，可認為計算達到收斂狀態。

船舶艉軸表面的線速度主要為0～12.56 m／s，所以在進行分析時將滑移壁面線速度數值確定在該范圍內。

2.4 湍流模型的選擇

通過計算得到軸承的雷諾數與臨界雷諾數，得出軸承在運轉過程中流體的流動狀態為湍流旋流狀態。為了更加精確地求解微溝槽內部的流體運動情況，往往需要考慮渦旋黏度的各向異性［20］。Reynolds Stress Model（RSM）算法可以綜合考慮強迫渦和自由渦所形成的組合渦態，更能模擬出真實的渦旋及流場，因此選用雷諾應力湍流計算模型。

2.5 模型尺寸無關性驗證

為了驗證模型尺寸的改變對分析結果趨勢的影響，例如流體跡線和壓力分布等，是否具有相似性，文中采用相同的邊界條件，通過改變整體模型的大小，對寬深比為3，深深比為0.03，深度分別為0.5、1、2、4 和8 mm 的溝槽模型進行分析。圖4 選取了深度為4 和8 mm 的結果進行展示，對于其他深度的溝槽結構具有相似的壓力和跡線分布。因此，在考慮實際的溝槽尺寸范圍內，改變模型的大小，其結果具有相似性。

3 結果與討論

3.1 速度的影響

圖5 分別顯示了在不同的滑移速度（軸表面線速度）下溝槽內部的流體流動狀態，此時軸承的深深比h1為0.03，寬深比h2為3。依據水流跡線可以得知溝槽內部潤滑介質的流動特征。軸的旋轉帶動軸承間隙內的流體向前流動，當流體到達溝槽部分時，高速入流近似為射流狀態。水流速度在近軸面為軸速，高速前進的水流在溝槽內部由于無壁面約束，會通過其邊界上活躍的湍流混合將溝槽內的流體卷吸進來而不斷擴大，并流向溝槽右端，此為進入溝槽內部水流的自由湍流作用。

圖5 不同速度下溝槽內部水流跡線Fig.5 Flow traces inside the trench at different velocities：（a）1 m／s；（b）1.5 m／s；（c）2 m／s；（d）3 m／s；（e）4 m／s

由于入流的自由湍流作用和平行剪切流間的不穩定性，水流截面積不斷增大，使得水流在溝槽內部沖擊溝槽內壁而折返，受到沖擊的溝槽內壁面形成高壓區。水流在溝槽底部沿著與轉速相反的方向流動，形成低速回流，并出現了第一個強迫渦旋1。在該渦內，渦核部分水流流速最低，沿渦核向外直到溝槽內壁水流速度逐漸增加。流體流動的曲率半徑小于溝槽內壁面的曲率半徑，小彎的存在使溝槽底部的水流不參與低速回流中，而是受低速回流的影響形成了漩渦3。

水流反向流動的過程中，依據伯努利定律，溝槽中的水流不斷匯入軸表面的高速水流中，形成循環，在此期間溝槽內部形成了多個渦旋且會促進溝槽上部的射流。渦旋2 和渦旋3 隨著速度的升高而不斷加強，渦旋2 最終穩定在溝槽中上位置，渦3 在生長的過程中不斷擠壓渦1 和渦2 使得渦1 逐漸減小，在此期間在渦2 附近形成了流體動壓效應，產生了承載力。

依據上述的溝槽內部流體流動變化過程，整理得到水潤滑軸承深溝槽潤滑機制示意圖如圖6 所示，其中靠近出口的溝槽內壁面高壓區是由于自由湍流的沖擊作用形成的，而非流體動壓效應。

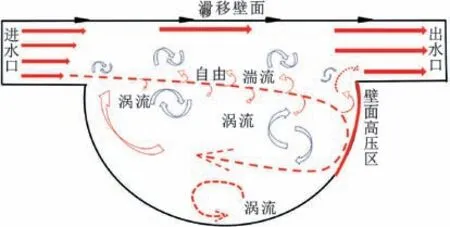
圖6 水潤滑軸承深溝槽潤滑機制Fig.6 Water－lubricated bearing groove lubrication mechanism

低轉速下，溝槽內部的介質水流動所形成的渦流較少，水流跡線沒有太大的彎曲。渦1 的回流使得在溝槽底部和靠近軸的地方再次生長出小的渦旋。流體速度越大，溝槽底部的渦旋3 的擠壓作用越強。不同寬深比下摩擦因數隨轉速的變化如圖7 所示，可以得出不同寬深比下摩擦因數均與轉速呈正相關。

圖7 不同寬深比下摩擦因數隨轉速的變化Fig.7 Variation of friction coefficient with rotational speed at different width－to－depth ratio

3.2 深深比的影響

圖8 顯示了在相對滑移速度為2 m／s，溝槽的寬深比為2 時，隨著溝槽深深比的改變，溝槽內部的水流跡線。當深深比很小時，強迫渦旋1 的低速回流很容易匯入從軸承間隙出現的射流中。渦旋2 近似為點渦，是一種理想的自由渦。

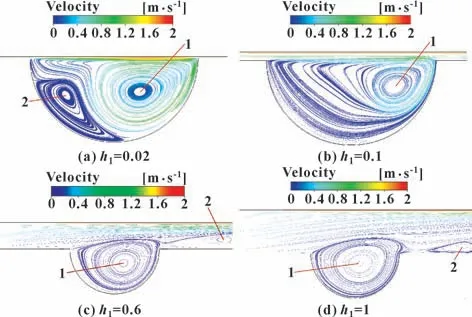
圖8 不同溝槽深深比下溝槽內部水流跡線Fig.8 Flow traces inside the trench for different trench depth ratios：（a） h1＝0.02；（b） h1＝0.1；（c） h1＝0.6；（d） h1＝1

隨著溝槽深深比的增大，軸的旋轉對軸承間隙內水流的文氏效應減弱，更少的水流碰撞到溝槽出口端的內壁上。在溝槽底部水流反向流動的過程中，不會生長出額外的渦旋，此時渦旋1 變為自由渦旋。溝槽深深比越大，來自軸承間隙的水流沖擊溝槽內壁越少，直至深深比超過某一數值（見圖8（c））；溝槽內水流受間隙內水流的影響，渦旋2 脫落，渦旋1 逐漸生長和擴大，直至該渦旋的尺寸大于溝槽的尺寸。自由渦旋1 會隨著深深比的增大而不斷生長（見圖8（c）（d）），且其循環區域的中心會先向溝槽出水口再向中心移動。

由圖8 所示的水流跡線圖可知，隨著溝槽深深比的增大，即溝槽結構的減小，渦旋1 會逐漸生長，直至漩渦尺寸大于溝槽的尺寸，進而使得軸承間隙內的流體在流經溝槽區域時由較大的流通面積變為較小的流通面積，在名義上形成了一個小的楔形區域，進而滿足了流體動壓潤滑的條件，在溝槽上部形成了局部的高壓區，提高了軸承的潤滑性能。其潤滑機制如圖9 所示。

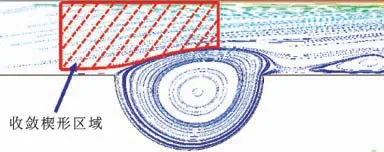
圖9 微溝槽提高水潤滑軸承潤滑性能機制Fig.9 Mechanism of micro－grooves improving the lubrication performance of water－lubricated bearing

圖10 顯示了溝槽深深比對溝槽內部水流壓力的影響，圖中壓力均為表壓。可知：深深比較小時，高壓區域出現在溝槽出水端邊緣位置（見圖10（a）（b）），在渦流的中心區域為低壓區域；隨著溝槽深深比的增大，溝槽內部流體壓力逐漸升高，直至形成流體動壓潤滑，整個溝槽內部壓差變小且均為正壓（見圖10（c）（d））。

圖10 不同溝槽深深比下溝槽內部壓力分布Fig.10 Pressure distribution inside the trench for different trench depth ratios：（a） h1＝0.02；（b） h1＝0.1；（c） h1＝0.6；（d） h1＝1

由圖10 可得，當溝槽深深比為0.6 時，溝槽內的水壓達到最大值；隨著深深比再度增大，溝槽內水壓反而會減小。因為渦旋1 的生長速度會變得越來越慢，故而在該部分所形成的流體動壓作用會先增大后減小。因此，溝槽深度與軸承間隙之間存在一個最佳的深深比。

圖11 顯示了不同溝槽深深比下溝槽內部的渦流黏度。可知隨著深深比的增加，渦流黏度減小，即溝槽內部湍流強度逐漸減弱。圖12 顯示了不同轉速下摩擦因數隨深深比變化的曲線。可見，隨著深深比的增加，即溝槽結構的減小，摩擦因數先減小而后增大；深深比為20～50 時摩擦因數增加較緩慢，深深比超過50 后摩擦因數增加變快；在深深比為2～5 時摩擦因數具有最小值。

3.3 寬深比的影響

圖13 顯示的為滑移壁面相對滑移速度2 m／s 時，隨著溝槽寬深比的改變溝槽內部的水流跡線。當寬深比很小時，只存在一個準強迫渦旋1（見圖13（a））；由于文氏效應的存在，渦旋1 的回流不斷匯入高速水流中（見圖13（b）—（d））。當溝槽深度增大時（即寬深比減小），軸表面高速水流對溝槽內流體的文氏效應減弱的同時，流體流動的曲率半徑小于溝槽內壁面的曲率半徑，形成小彎，使位于槽底的自由渦旋2 和溝槽回流區域負壓區的增大（見圖13（b）—（d））。

圖14 顯示了寬深比對溝槽內部水流壓力的影響，圖中壓力均為表壓。由于文中分析時所采用的深深比較小，所以高壓區域出現在溝槽右上位置，漩渦的中心區域為低壓區域。隨著寬深比的減小，溝槽內部最低水壓數值變化不大，低壓區所占的比例范圍會擴大。因此，溝槽深度越大，溝槽內部水壓越小，軸承的潤滑性能越差。

圖14 不同寬深比下溝槽內部壓力分布Fig.14 Pressure distribution inside the trench for different widthto－depth ratios：（a） h2＝7.5；（b） h2＝5；（c） h2＝3；（d） h2＝2.5

圖15 顯示了不同溝槽寬深比下溝槽內部的渦流黏度。溝槽內流體黏度隨溝槽寬深比的減小而減小，表征了湍流效應的減弱，即流體對流動所表現的阻力越來越小。

圖15 不同寬深比下溝槽內部渦流黏度Fig.15 Vortex viscosity inside the trench with different width－todepth ratios：（a） h2＝7.5；（b） h2＝5；（c） h2＝3；（d） h2＝2.5

3.4 水潤滑軸承溝槽內部壓力分布

通過創建具有溝槽結構的水潤滑軸承分析模型，探究溝槽內部的壓力分布。所采用的溝槽結構為橢圓形溝槽，軸承和溝槽的具體參數如表1 所示，設定軸承的偏心率為0.5。圖16 展示了當轉速250 r／min時，水潤滑軸承內部水域壓力分布云圖。

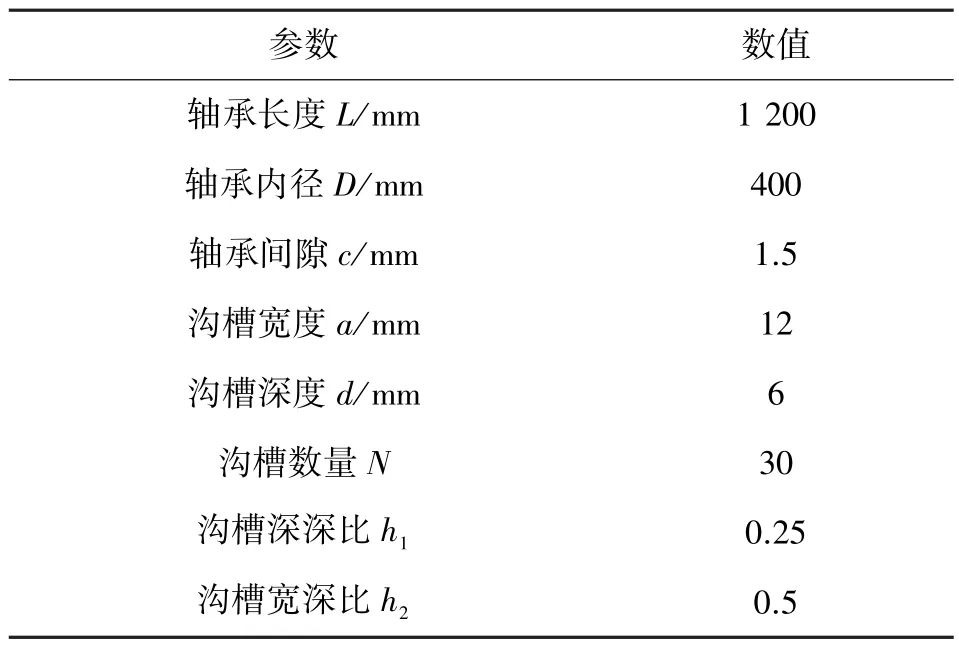
表1 軸承和溝槽結構參數Table 1 Structural parameters of bearings and grooves

圖16 軸承內部水域水膜壓力分布Fig.16 Water film pressure distribution in the internal waters of the bearing

通過對溝槽內流體流動得出的結論，如圖6 所示，溝槽內部高壓區會出現在靠近溝槽出口的位置。圖17 展示的分別為某高壓和某低壓區溝槽內壁面的水壓分布情況，顏色所代表的壓力范圍與圖17 相同。圖17 中軸的轉速方向為徑向方向向下。經驗證溝槽內壁高壓區域出現在溝槽出口端，溝槽底部大部分為低壓區域，與文中潤滑理論相吻合，從而驗證了文中潤滑理論的準確性。

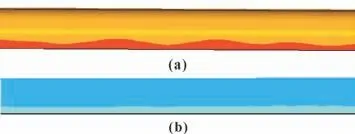
圖17 某高壓區溝槽（a）和某低壓區溝槽（b）內壁面壓力分布Fig.17 Pressure distribution on the inner wall surface of a trench in the high－pressure area（a）and a trench in the low－pressure area（b）

4 結論

建立簡化后的船舶水潤滑軸承溝槽模型，研究結構參數對水潤滑軸承溝槽內部流動特征的影響，揭示溝槽結構對船用水潤滑軸承潤滑特性的影響機制。主要結論如下：

（1）軸轉速越高，溝槽內位于溝槽底部的渦旋會逐漸生長，其擠壓溝槽內部其余渦旋和水域的能力越強。

（2）當溝槽結構很小時，溝槽內部的水流形成一個單獨的大渦旋，該渦旋的尺寸大于溝槽尺寸。來自軸承間隙的水流在流經溝槽結構時會形成楔形收斂區，形成微動效應，提高了該部分的水膜壓力和軸承承載能力。

（3）溝槽寬深比越小，即溝槽深度越大，溝槽內部水流更容易形成多個渦旋，在降低流體黏度的同時也會進一步增加溝槽內的負壓區范圍，使軸承水膜的壓力不連續。