偏載下大長徑比水潤滑軸承分布式動特性參數識別方法?

程奇志 歐陽武 黃志偉 彭偉才

（1.武漢理工大學船海和能源動力工程學院 湖北武漢 430063；2.武漢理工大學交通與物流工程學院 湖北武漢 430063；3.國家水運安全工程技術研究中心，可靠性工程研究所 湖北武漢 430063；4.中國艦船研究設計中心船舶振動噪聲重點實驗室 湖北武漢 430064）

船舶動力系統中，推進軸系主要用于傳遞主機動力和螺旋槳推力，是保障船舶正常運行的關鍵部件。其中水潤滑艉軸承作為螺旋槳軸的重要支撐部件，具有優良的減振性能、較小的摩擦因數和無污染等優點［1－2］。作為螺旋槳－軸系－主機－船體之間傳遞振動能量的關鍵元件，艉軸承的動力學特性影響著推進軸系的動力學行為，直接關系到推進系統運轉質量的優劣［3－5］。準確識別艉軸承動特性參數有利于提高推進軸系動特性預測和提出減振降噪方法的置信度，對實現船舶機艙振動故障診斷有重要意義。

在過去的幾十年里，國內外對滑動軸承的動態系數識別方法已經做過大量的工作，根據是否人為施加激勵，滑動軸承動特性參數的識別方法可分為外部激振法和不平衡質量法。不平衡質量法不需要外部激振，系統的激振來源于軸承－轉子系統自身的不平衡力；而外部激振法包括穩態激振法和瞬態激振法，其中穩態激振法包括單頻兩次激勵法、復合激勵法、多頻激勵法，瞬態激振法則包括脈沖激振法和寬帶激振法［6］。馬石磊等［7］利用不平衡質量法研究了轉速、供水壓力等因素對軸承動特性參數的影響。KUMAR REDDY 等［8］采用單頻兩次激振法識別了可傾瓦軸承動特性參數，測量值與基于TEHD 模型計算得到的仿真值相差約10%。楊利花等［9］建立了新型彈性箔片動壓氣體軸承性能測試實驗臺，采用復合激振法研究了不同激振頻率對軸承動特性參數的影響。CHATTERTON等［10］采用多頻激振法研究了激振頻率與可傾瓦軸承動特性參數的關系。CHILDS 和HALE［11］分析了能量集中的頻帶信息，利用最小二乘法解出動特性參數。MATTA 和ARGHIR［12］利用沖擊錘產生的脈沖激勵和測量得到的位移響應之間的聯系，識別了徑向軸承的動特性參數。

綜上所述，目前軸承集中動特性識別方法的研究較多。普通徑向軸承長徑比（軸承長度與內徑的比值）為0.8～1.2，而艉軸承長徑比達到了2～4［13］。另外，在螺旋槳的懸臂作用下，轉軸會發生傾斜。軸傾斜和大長徑比這2 個因素將導致軸承沿軸向出現潤滑分區的現象，軸承動特性呈現分布特征，目前將軸承假設為單支點的集中動特性識別方法難以滿足艉軸承動特性識別需求。為此，文獻［14］提出了識別軸承兩端動特性參數的方法，但對軸承模型簡化較多，僅識別了軸承垂直方向的主剛度和主阻尼系數。在此基礎上，文獻［15］建立了可以模擬軸彎曲的軸承動特性試驗臺，以轉子－軸承系統力平衡方程為基礎提出軸承動特性參數的識別方法，為軸承分布式動特性識別提供了新思路，但將假設的兩段軸承之間的相互作用被忽略了。

為此，本文作者以偏載下大長徑比水潤滑軸承為研究對象，建立了兩支點分布式動力學模型，綜合考慮力平衡和力矩平衡方程，提出了一種基于正反動力學問題水潤滑軸承動特性識別方法，利用仿真試驗分析了加載信號和位移信號擾動對識別誤差的影響。

1 水潤滑軸承分布式動特性參數識別模型

1.1 動力學模型

將軸承沿軸承垂直中心線劃分為2 個單元，假設軸承有2 個等效支點支撐著轉軸，形成兩支點分布式動特性模型。大長徑比水潤滑軸系系統動力學模型如圖1 所示，水潤滑軸承左側由激振裝置提供動態激振力fy，右側由配重盤模擬螺旋槳自重f0，l1、l2分別為左右兩端水潤滑軸承到轉子質心的距離，l3、l4分別為動態激振力和靜載力施加位置到轉子質心的距離。

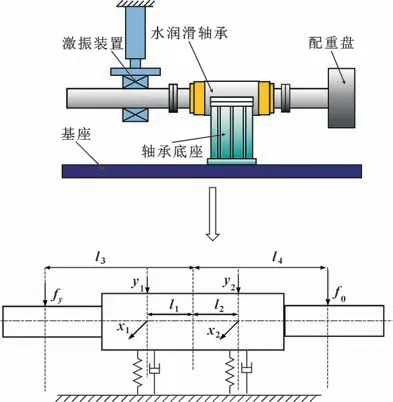
圖1 大長徑比水潤滑軸承系統的動力學模型Fig.1 Dynamic model of water lubricated bearing system

當轉子轉速為Ω時，對軸施加垂直激振力fy后，可獲得左右兩端水潤滑軸承中心測量的轉子運動x1、x2、y1和y2。基于上述簡化后的模型，通過力和力矩平衡可得：

式中：xc和yc分別為轉子質心在水平和豎直方向上的運動；m為轉子和軸承的總質量；kx1、ky1，cx1、cy1分別為左側（電機端）水潤滑軸承的剛度和阻尼參數；kx2、ky2、cx2、cy2分別為右側（懸臂端）水潤滑軸承的剛度和阻尼參數；θx和θy為轉子傾斜角；It和Ip分別為轉子徑向慣性力矩和轉子極慣性力矩。

轉子質心的運動：

轉子在x軸和y軸上的傾斜角：

式中：L為左右兩端水潤滑軸承的中心距離，L＝l1＋l2。

聯立公式（1）—（8）并進行FFT 變換，可得：

1.2 反問題和仿真驗證

在軸上施加激勵力fy，一次激振可以建立4 個方程，對4 個方程進行FFT 變換，求解可得到8 個剛度和阻尼系數。將通過負載和位移響應得到剛度阻尼系數的計算過程稱為反問題。等式（9）進行線性化處理可得到。

方程式中：

方程式（10）中，Qi和Pi已知，i＝x或y。求解矩陣方程Pi＝Qi－1Ni來獲得軸承動特性參數。

為驗證文中識別方法的可信度，參照文獻［16］中的參數進行仿真。將文獻［16］中的標準值與不添加干擾下的反問題識別結果進行對比，結果如表1 所示。可知，剛度和阻尼系數識別最大誤差絕對值小于0.3%，表明動特性識別方法是可信的。

表1 剛度和阻尼系數標準值和識別值比較Table 1 Comparison of standard and identification values for stiffness and damping coefficient

2 試驗對象和試驗臺

試驗軸承結構如圖2 所示，以長度200 mm、直徑50 mm 的水潤滑軸承為研究對象，建立水潤滑軸承動特性識別試驗臺，如圖3 所示。該試驗臺包括驅動電機、扭矩儀、支撐軸承、加載系統、試驗軸承、配重盤和限位裝置組成。其中試驗軸承為水潤滑軸承，支撐軸承為滾動軸承。試驗轉速范圍0～250 r／min，配重盤質量25 kg，試驗臺基本參數如表2 所示。

圖2 試驗軸承實物圖Fig.2 Physical picture of test bearing

3 水潤滑軸承分布式動特性識別方法仿真試驗

3.1 仿真試驗方法

為檢驗軸承動特性參數識別方法的可行性和了解外部干擾對動特性參數的影響，開展了仿真試驗研究。仿真試驗流程如圖4 所示。首先，給定激振力F、軸承剛度k和阻尼c，對動力學模型進行正問題求解，獲得位移響應Q；然后，對F和Q添加幅值誤差或者相位誤差，在動力學模型進行反問題求解，得到軸承剛度和阻尼的識別值k和c。通過對比給定值和識別值，分析識別精度影響情況。

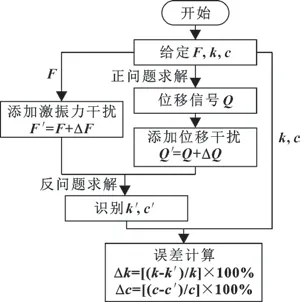
圖4 軸承動特性識別方法仿真試驗流程Fig.4 Dynamic characteristic parameter identification process

軸承動特性試驗時，采集信號的誤差包含系統誤差和偶然誤差。在仿真試驗中，通過給力和位移值主動添加干擾，來模擬測試誤差。具體是在頻域中給幅值和相位添加偏差：

式中：A0和?0為采集信號干擾前的幅值和相位；ΔA和Δ?分別為采集信號受干擾造成的幅值偏差和相位偏差；A1和?1為采集信號干擾后的幅值和相位。

3.2 仿真試驗結果

仿真試驗中F為171exp（－j0.886π），軸承的剛度和阻尼值如表3 所示。

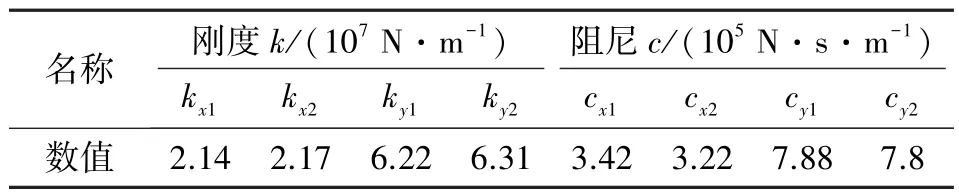
表3 剛度和阻尼系數輸入值Table 3 Input values of stiffness and damping coefficient

3.2.1 激振力擾動對識別精度的影響

激振力幅值擾動對剛度阻尼識別值相對誤差影響如圖5（a）所示，隨著激振力振幅擾動的增加，剛度和阻尼系數的識別誤差線性增加。相同擾動下，阻尼系數誤差的變化值大于剛度系數誤差的變化值。如果剛度和阻尼系數的識別誤差小于10%，則激振力的幅值擾動應小于16%。

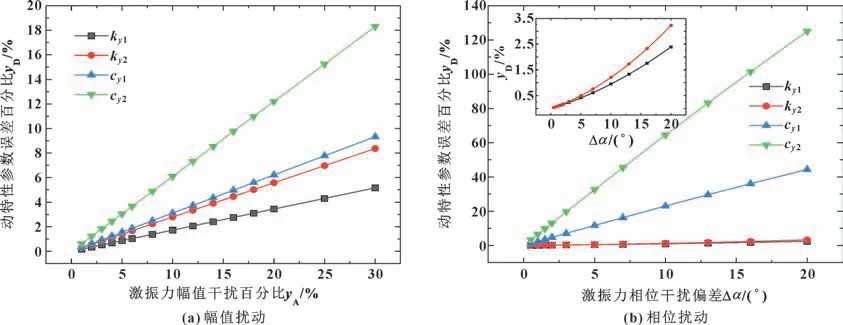
圖5 Fy幅值擾動和相位擾動對剛度阻尼識別值相對誤差影響Fig.5 Influence of Fy amplitude disturbance（a）and phase disturbance（b）on relative error of stiffness and damping identification value

激振力相位擾動對剛度阻尼識別值相對誤差影響如圖5（b）所示，激振力相位擾動對剛度系數的影響較小，對阻尼系數的影響較大。隨著激振力相位擾動的增加，剛度和阻尼系數的識別誤差逐漸增加，剛度系數誤差的增長速率也隨相位的增大而增大。對于水潤滑軸承，如果主阻尼的識別誤差小于20%，則激振力的相位干擾應小于3°。

3.2.2 位移信號擾動對識別精度的影響

位移幅值擾動對剛度阻尼識別值相對誤差影響如圖6（a）所示，隨著位移幅值擾動的增加，剛度和阻尼系數的識別誤差增加。同一幅值干擾下，阻尼系數和剛度系數的識別誤差基本相同。如果剛度和阻尼系數的識別誤差小于10%，則位移幅值擾動應小于10%。

圖6 位移擾動對剛度阻尼識別值相對誤差影響Fig.6 Influence of displacement amplitude disturbance（a）and phase disturbance（b）on relative error of stiffness and damping identification value

位移相位擾動對剛度阻尼識別值相對誤差影響如圖6（b）所示，位移信號的相位擾動對剛度系數的影響較小，對阻尼系數的影響較大，剛度和阻尼系數都會隨著位移信號的相位擾動的增大而增大。對于水潤滑軸承，如果阻尼的識別誤差小于20%，則位移幅值的相位干擾應小于1°。

4 水潤滑軸承分布式動特性識別試驗

圖7 展示了軸承剛度和阻尼隨轉速的變化。可知，垂直方向剛度大于水平方向剛度，垂直方向阻尼大于水平方向阻尼，這與水膜承受垂向載荷有關。另外懸臂端的剛度和阻尼大于對應電機端的剛度和阻尼。當轉速增加時軸承兩端阻尼呈下降趨勢，剛度略微減小，這是因為當轉速增加時，軸承由混合潤滑狀態過渡到動壓潤滑狀態，水膜厚度增大使剛度減小，潤滑區域增大使阻尼減小。

5 結論

為解決偏載下大長徑比水潤滑軸承分布式動特性參數識別問題，建立了水潤滑軸承的兩支點分布式動力學模型，基于動力學的正、反問題的計算方法，提出了一種識別水潤滑軸承動態系數的方法，分析了加載信號擾動和位移信號擾動對辨識精度的影響，并進行仿真驗證了該動特性參數識別方法的準確性。結論如下：

（1）隨著激振力振幅擾動的增加，剛度和阻尼系數的識別誤差線性增加。激振力相位擾動對剛度系數的影響較小，對阻尼系數的影響較大。

（2）隨著位移幅值擾動的增加，剛度和阻尼系數的識別誤差增加。位移信號的相位擾動對剛度系數的影響較小，對阻尼系數的影響較大。

（3）仿真計算結果表明，若要求剛度和阻尼的識別誤差小于10%，則激振力和位移信號的擾動幅值應小于10%；若要求剛度和阻尼的識別誤差小于20%，則這2 個信號的擾動相位擾動偏差應小于1°。