例說對數型函數的最值的應用

■薛忠云

函數的最值是函數的重要性質之一,下面從六個方面介紹對數型函數的最值的應用,希望對大家的學習有所幫助。

一、已知函數的最值求參數的值

例1若函數f(x)=2logax+2(a>0,且a≠1)在區間上的最大值為6,則a的值為_____。

二、已知函數的最值求其他函數的最值

例2已知函數f(x)=x-lnx的最小值為1,則函數的最小值為____。

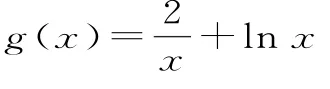
評注:將f(x)轉化為f(t)=t-lnt,令得到f(t)=y=g(x)-ln2,結合已知函數最小值即得目標函數的最小值。

三、已知函數有最值求參數的取值范圍

例3若函數f(x)=loga(-x2-ax-1)(a>0,且a≠1)有最大值,則實數a的取值范圍為_____。

因為內層函數y=-x2-ax-1是開口向下的拋物線,又f(x)有最大值,所以外層函數f(x)為增函數,且內層函數的最大值為正數,所以解得a>2。故實數a的取值范圍為(2,+∞)。

評注:復合函數中,內層函數的值域是外層函數的定義域。

四、已知函數的值域為R 求參數的取值范圍

例 4 已 知 函 數f(x) =的值域為R,則實數a的取值范圍是_____。

當x≤1 時,f(x)=-log2(2-x)為單調遞增函數,且f(1)=0。當x→-∞時,f(x)趨近于負無窮大,故當x≤1 時,f(x)的取值范圍是(-∞,0]。

當x>1時,

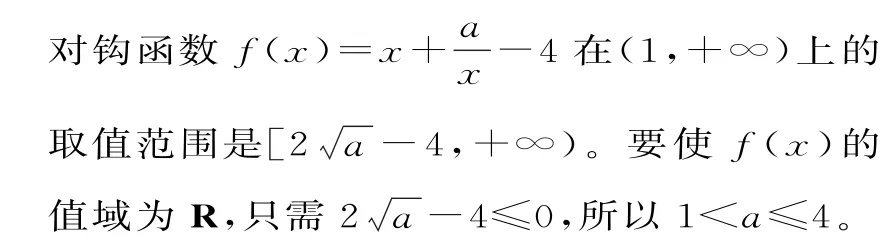
當a≤1時,對鉤函數在(1,+∞)上單調遞增,其值域是(f(1),+∞)=(a-3,+∞),要使f(x)的值域為R,只需a-3≤0,可得a≤3,所以a≤1,滿足題意。

五、已知函數的最大值與最小值的關系求參數的取值范圍

六、已知函數沒有最小值求參數的取值范圍