指數(shù)冪運(yùn)算有奇招
2023-11-29 10:02:02黃海英
中學(xué)生數(shù)理化·高一版 2023年11期
■黃海英
指數(shù)冪是研究指數(shù)函數(shù)的前提,掌握了指數(shù)冪的運(yùn)算方法和技巧是進(jìn)一步學(xué)習(xí)指數(shù)函數(shù)的基礎(chǔ),那么怎樣才能提高指數(shù)冪的運(yùn)算技巧呢?
一、平方與配方
指數(shù)運(yùn)算與根式運(yùn)算,從本質(zhì)上看都是實(shí)數(shù)運(yùn)算,因此它們的運(yùn)算離不開實(shí)數(shù)運(yùn)算公式,尤其是完全平方公式的靈活運(yùn)用。
例1已知,求下列各式的值:(1)m+m-1。(2)m2+m-2。(3)m3+m-3。
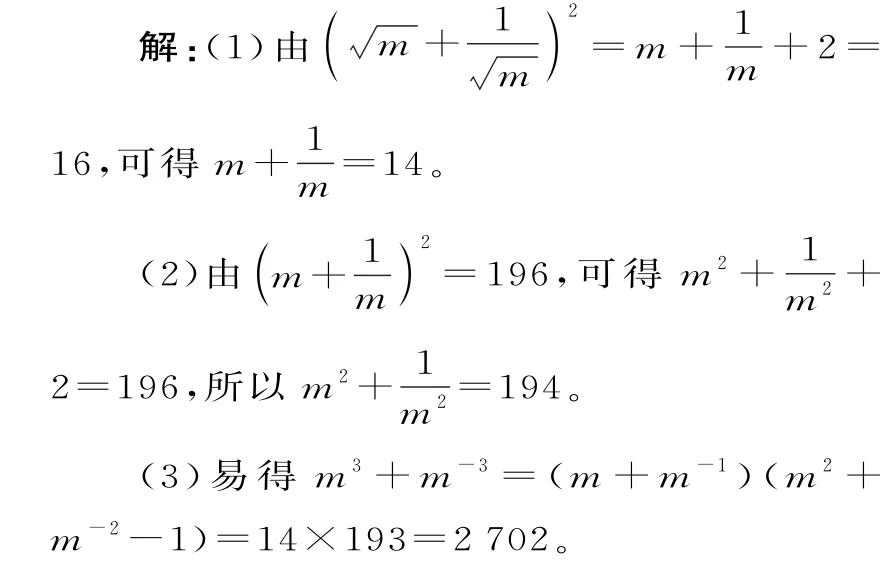
二、轉(zhuǎn)化為指數(shù)冪的形式
指數(shù)式與根式是可以互相轉(zhuǎn)化的,將根式轉(zhuǎn)化為指數(shù)冪的形式,能更好地利用指數(shù)冪的運(yùn)算公式,使運(yùn)算更有效。

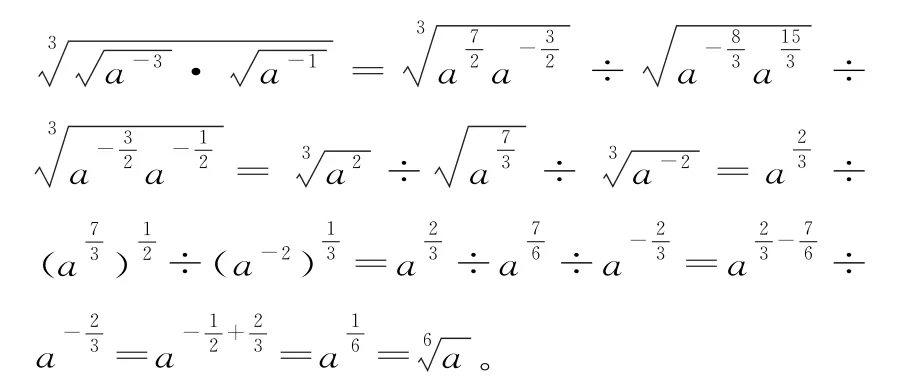
三、整體代換
在指數(shù)冪運(yùn)算中,有時(shí)在條件中會(huì)出現(xiàn)多個(gè)字母的輪換式,這時(shí)可利用整體代換,使得解題最有效、簡捷。

四、巧用“1”的變形
在數(shù)學(xué)解題中,“1”是一個(gè)萬變高手,在指數(shù)冪運(yùn)算中,它可轉(zhuǎn)化為兩個(gè)互為倒數(shù)的數(shù)的積,從而為利用有關(guān)運(yùn)算公式創(chuàng)造條件。
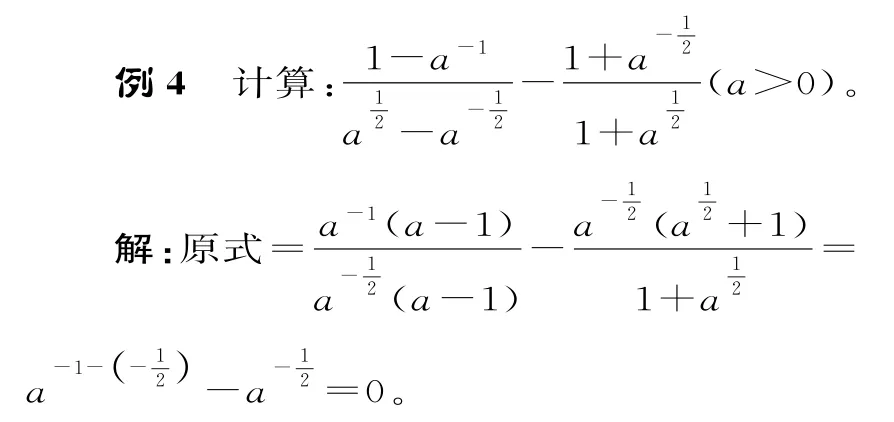
猜你喜歡
小學(xué)生學(xué)習(xí)指導(dǎo)(低年級(jí))(2022年9期)2022-10-08 03:12:02
中學(xué)生數(shù)理化·中考版(2022年8期)2022-06-14 06:55:52
中等數(shù)學(xué)(2022年2期)2022-06-05 07:10:50
今日農(nóng)業(yè)(2021年1期)2021-11-26 07:00:56
小學(xué)生學(xué)習(xí)指導(dǎo)(低年級(jí))(2021年4期)2021-07-21 01:59:26
小學(xué)生學(xué)習(xí)指導(dǎo)(低年級(jí))(2020年6期)2020-07-25 02:31:36
甘肅教育(2020年12期)2020-04-13 06:24:46
小學(xué)生學(xué)習(xí)指導(dǎo)(低年級(jí))(2018年9期)2018-09-26 05:59:44
作文周刊·小學(xué)一年級(jí)版(2018年17期)2018-09-10 02:39:46
瘋狂英語·新讀寫(2018年2期)2018-09-07 09:32:10

