高斯過程回歸泊松多伯努利衍生濾波器

宋營營，宋驪平

西安電子科技大學 電子工程學院，西安710071

目標跟蹤就是在一定先驗信息的基礎上，通過雷達、激光、聲吶等各種類型傳感器所獲得的量測信息，對目標狀態進行遞推估計，從而獲得目標的數量以及目標的位置、速度等運動狀態信息。目標跟蹤技術無論在軍事還是民事方面都有著廣泛的應用。隨著激光雷達、合成孔徑雷達、相控陣雷達等高分辨傳感器的涌現，出現了所謂的擴展目標跟蹤問題。擴展目標和點目標最大的差別就是具有更多的狀態特征，其主要體現在量測建模方式上。經過多年的發展，針對不同類型的目標，專家和學者們提出了形形色色的擴展目標建模方法，文獻[1]總結了現階段常用的擴展目標跟蹤方法。目前，對擴展目標的建模主要有基于隨機矩陣（random matrices，RM）[2]和基于隨機超曲面型模型（random hypersurface model，RHM）[3]等方法。隨機矩陣方法使用一個對稱正定矩陣來描述目標形狀，在高斯逆威舍特（Gaussian inverse Wishart，GIW）[4]濾波提出后得以應用在擴展目標跟蹤中。文獻[5]采用伽馬高斯逆威舍特（Gamma Gaussian inverse Wishart，GGIW）為擴展目標建模，提出了一種多模型的伽馬高斯逆威舍特-泊松多伯努利混合算法。RHM 與RM 的不同在于，RHM 彌補了隨機矩陣忽略傳感器噪聲的缺點，用比例因子將量測源建模在目標的縮小輪廓上，這兩者都可以對橢圓形狀目標進行建模。針對不規則形狀的建模，西安交通大學的蘭劍等人[6]提出了多隨機矩陣模型，該模型使用多個橢圓的組合來近似目標形狀。還有一類方法是采用徑向函數對擴展目標建模。由于徑向函數能夠表示任意角度下目標運動中心與目標輪廓之間的距離，該方法在理論上適合對任何星凸形狀的目標建模。高斯過程（Gaussian process，GP）是由無限維的正態分布函數構成的隨機過程，并被廣泛應用于機器學習[7-8]。Wahlstr?m等人[9]假設不同角度下的目標徑向函數值之間服從多維正態分布，首次將高斯過程回歸（Gaussian process regression，GPR）代入貝葉斯公式，提出了用于理想環境下的高斯過程-擴展卡爾曼（Gaussian process-extended Kalman filter，GP-EKF）單擴展目標跟蹤算法。基于高斯過程回歸的多擴展目標跟蹤算法[10]也隨之出現。經過多年的發展，擴展目標建模技術已趨于成熟，各種不同的建模方式已經可以滿足真實場景的需要。

20世紀90年代，Mahler提出了有限集統計學（finite set statistics，FISST）[11-13]，將統計學中的數學概念與目標跟蹤技術相結合，為多目標跟蹤領域的發展提供了新的思路。基于隨機有限集框架下的多目標跟蹤方法，將多目標狀態與傳感器量測分別建模為兩個獨立的隨機有限集（random finite sets，RFS），即狀態RFS與量測RFS。在此基礎上一系列基于RFS框架的濾波算法被陸續提出，例如基于一階統計矩近似的概率假設密度（probability hypothesis density，PHD）[14]濾波器和勢概率假設密度（cardinality probability hypothesis density，CPHD）[15]濾波器，以及基于有限集概率密度近似的多目標多伯努利（multi-target multi-Bernoulli，MM）[16]濾波器。2015 年，Williams 提出了用于點目標跟蹤的面向軌跡的泊松多伯努利（trajectory-oriented Poisson multi-Bernoulli，TO-PMB）濾波器和基于變分近似法的PMB 濾波器[17]。2015年，Williams[18]又提出一種新的全貝葉斯濾波算法，通過概率生成泛函（probability generating function，PGF）完成了對泊松點過程（Poisson point process）以及多伯努利混合（multi-Bernoulli mixture，MBM）相互獨立的兩部分的遞推，隨后將多目標狀態的概率密度用這兩部分來表示，證明這種全貝葉斯隨機集的概率密度是先驗共軛的[19]。2021 年，Xia 等人[20]將TO-PMB 濾波器和基于變分近似法的泊松多伯努利（Poisson multi-Bernoulli，PMB）濾波器推廣到擴展目標，提出擴展目標PMB濾波器。該濾波器是基于PMB的共軛先驗分布，其更新步得到泊松多伯努利混合（Poisson multi-Bernoulli mixture，PMBM）[21]后驗形式，將多伯努利混合（MBM）部分近似為單個多伯努利形式，從而獲得PMB后驗分布，實現預測和更新步的遞推過程。更新步涉及了PMBM的后驗形式，保留了PMBM 考慮所有數據關聯假設的優點，因此PMB 濾波器在保持良好濾波性能的同時，具有比PMBM 更高效的計算能力。隨機集理論的出現為多目標跟蹤的快速發展奠定了堅實的基礎。

在擴展目標跟蹤中，衍生是擴展目標運動的一種可能情況。文獻[22]提出了擴展目標/群目標的衍生模型和合并模型，該衍生模型假設衍生事件是由一個目標衍生出兩個目標，且發生在量測生成時。文獻[23]提出了兩種衍生模型，推導了在衍生目標分布服從這兩種模型的情況下衍生概率密度的具體表達式，提出了能對含衍生情況的擴展目標進行跟蹤的CPHD濾波器。文獻[24]提出了一種多假設衍生模型，可以預測多種可能的衍生事件。含衍生目標跟蹤算法的廣義標簽多伯努利（generalized labeled multi-Bernoulli，GLMB）濾波器[25]中指出衍生目標和新生目標不同的特征在于衍生目標與原目標距離近，初始速度相同，速度變化快，迅速偏離原目標預測門限的衍生目標應當作新生目標處理。文獻[26]將衍生目標描述為未知目標，由泊松點過程建模，考慮原目標與衍生目標的關系，提出了含衍生的PMB濾波器，然而該濾波器未考慮到目標形狀建模。

擴展目標常用的建模方式是隨機矩陣[27]，文獻[20]就是采用隨機矩陣實現橢圓形狀的擴展目標跟蹤，本文稱為GGIW-PMB算法。為了對非橢圓形狀擴展目標進行準確的估計，本文引入GPR，通過擴展卡爾曼技術實現GPR 的遞歸，將結合了GPR 的擴展目標建模方法稱為高斯過程回歸-伽馬高斯混合（Gaussian process regression-Gamma Gaussian mix，GPR-GGM）模型，可用于非橢圓形狀目標的建模。另外，考慮到擴展目標的衍生情況，本文提出了一種衍生目標檢測及建模方法，將目標關聯量測數的變化作為衍生假設的依據，根據真實場景關系計算衍生目標狀態，并對衍生目標采用GPR-GGM模型建模。

1 GPR-GGM模型

在GPR-GGM 模型中，擴展目標的運動狀態、量測率分別由高斯分布和伽馬分布來描述，目標的量測模型采用高斯過程回歸模型。目標的狀態記為運動狀態和擴展狀態的組合，即。其中，目標的擴展狀態由一組不同角度下目標原點到目標邊緣的距離值構成，即[r1,r2,…,rM]。

假設目標的運動狀態和擴展狀態相互獨立，那么目標狀態轉移方程可以寫成以下形式：

量測模型采用高斯過程回歸模型，如下式所示：

其中，p(θk)是方向向量，表達式為：

式（3）表示的量測模型對應的觀測方程為非線性方程，需要進行非線性處理。文獻[9]中采用擴展卡爾曼濾波器實現了GP-EKF單擴展目標跟蹤，本文延續文獻[9]中的方法對于量測模型的處理也使用擴展卡爾曼濾波器，因此，量測轉移矩陣Hk的計算公式為：

那么，就可以得到擴展目標狀態估計xk|k和對應誤差協方差矩陣Pk|k的計算公式：

采用GPR-GGM模型的擴展目標跟蹤中，k時刻目標的概率密度通過泊松率γk和目標狀態xk計算，即：

其為伽馬高斯混合形式。

2 衍生模型

本文提出一種新的衍生模型，包括衍生事件的判別準則、衍生目標的檢測方法以及衍生目標概率密度的計算。

如何判斷某一時刻觀測區域中是否發生衍生事件是衍生目標跟蹤中的一個重要問題。在發生衍生的時刻，衍生目標與原目標距離很近，無法區分衍生目標與原目標的量測，使原目標在擴展形態上發生突變，其擴展范圍明顯增大；而發生衍生的下一時刻，衍生目標與原目標分離，可以區分量測，原目標的擴展形態又恢復正常。根據這一特性，提出一種可以對某一時刻觀測區域中各個目標是否發生衍生進行判斷的準則。本文根據量測數的變化設計衍生假設函數，k時刻目標i的衍生假設函數為sk,i=s(Nk-1,i,Nk,i)，其中Nk-1,i是k-1 時刻與目標i關聯的量測數，Nk,i是k時刻與目標i關聯的量測數。當sk,i大于設定閾值時，假設k時刻目標i發生了衍生。

衍生事件發生后，如何檢測到衍生目標也需要研究。有的衍生目標檢測方法是將衍生目標看作新生目標進行檢測，但多數新生目標建模方法都是假設新生目標在指定位置出現，而衍生目標位置大多是未知的，例如飛機發射導彈，導彈作為衍生目標，其出現與否無法預知。若新生目標建模時假定觀測區域所有位置都可能出現新生目標，將導致跟蹤算法計算量急劇增長，因此不應將衍生目標視為新生目標來建模和檢測。

考慮到衍生事件多發生在特定場景下，例如在飛機發射導彈場景中，衍生發生時刻導彈會繼承飛機的運動狀態，那么可以將飛機的狀態賦予導彈，作為導彈這一衍生目標的初始狀態。因此，在做出衍生假設后，根據衍生目標與原目標在衍生事件發生時距離相近、速度近似這一特性，計算出衍生目標的初始狀態，在下一時刻通過計算出的衍生目標狀態進行更新，就能實現衍生目標的檢測和跟蹤。

假設k時刻擴展目標i發生了衍生，那么衍生目標的初始狀態設定為，其中xk,i為k時刻擴展目標i的狀態。在此基礎上，采用GPR-GGM 模型為衍生目標建模，以實現對其擴展形態的跟蹤。將得到的衍生目標參數代入式（10）可以得到k時刻衍生目標的概率密度函數，如下所示：

3 基于高斯過程回歸的泊松多伯努利衍生濾波器

假設給定k-1 時刻的后驗密度表示為：

算法流程：

步驟1預測。

用sk,i對觀測場景中的各個目標是否發生衍生進行判斷，假設目標i發生衍生，記得到的衍生目標為iΓ，放入衍生目標索引集IΓ。

步驟2更新。

對式（12）的預測密度更新后得到PMBM形式的后驗概率密度，表達式為：

更新后的泊松隨機有限集概率密度為：

其中，vΓ(xk)表示衍生目標強度。假設IΓ中有NΓ個目標，那么衍生目標強度的表達式為：

多伯努利混合隨機集中參數的計算方法與其對應目標類型，以及該目標是否被檢測到有關。對于上一時刻已檢測到的目標，這一時刻該目標可能漏檢或者產生新的量測。Aj表示全局假設j對應的數據關聯空間，每一個Aj中有多個?。? 是包含目標和量測索引的集合用于表示目標和量測之間的關聯關系，C?為? 中量測索引對應的量測集合。如果在假設j中，目標i漏檢，即? ∈Aj,?={i},C?=?，那么更新多伯努利隨機集的參數計算公式為：

如果在假設j中，目標i被檢測到，即? ∈Aj,i∈?,C?≠?，那么更新多伯努利隨機集的參數計算公式為：

如果在假設j中，? 中有量測索引和新生目標標號，但沒有存活目標標號和衍生目標標號，即? ∈Aj,? ∩(I∪IΓ)=?,? ∩Ib≠?,C?≠?，也就是檢測到新目標量測的情況，那么更新多伯努利隨機集的參數計算公式為：

如果在假設j中，? 中有量測索引和衍生目標標號，但沒有存活目標標號和新生目標標號，即? ∈Aj,? ∩(I∪Ib)=?,? ∩IΓ≠?,C?≠?，也就是檢測到衍生目標量測的情況，那么更新多伯努利隨機集的參數計算公式為：

如果在假設j中，? 中有量測索引，但沒有存活目標標號、新生目標標號和衍生目標標號，即? ∈Aj,? ∩(I∪Ib∪IΓ)=?,C?≠?，也就是檢測到雜波的情況，那么更新多伯努利隨機集的參數計算公式為：

更新后，每個多伯努利隨機集中表示已檢測到目標數目的值與預測的值相同，表示新潛在檢測目標個數的值變為| IjI|。

步驟3變分合并。

變分合并技術[17]是解決MB 近似問題的一種技術。GPR-PMBS濾波器的預測密度如式（13）所示，經過貝葉斯更新后得到PMBM形式的后驗概率密度如式（17）所示，要實現遞歸，需要使用變分合并技術將式（17）中的MBM密度進行變分合并得到MB密度。將式（17）中的MBM 密度用式（30）表示，記為f(X)，變分合并后得到的MB密度用式（31）表示，記為g(X)。

MBM近似的目的就是找到使得f(X)和g(X)之間的KL 散度最小的g(X)，也就是找到使得下式最小的g(X)：

變分合并技術將g(X)的求解問題轉換為下式的求解：

將f(X)中的伯努利與g(X)中的伯努利之間的對應關系視為缺失數據q(π)，那么式（33）所示優化問題的求解相當于尋找最佳缺失數據分布(π)。

經過整理，式（33）變為：

解決式（34）所示優化問題的標準方法是塊坐標下降，在gl(Xl)（M 步）和qj(πj)（E 步）的最小化之間交替進行。簡化缺失數據的表達式之后可以得到如下M步和E步新的表示。

M步表示為：

E步表示為：

其中，q(h,l)滿足以下條件：

此時，MBM近似問題轉化為M步和E步塊坐標下降，可以使用單純形算法[21]等方法得到近似后的MB密度。

4 仿真分析與比較

基于GGIW建模的PMB與PMBM算法是當前主流方法中效果最好的兩種多擴展目標跟蹤算法，二者的區別在于GGIW-PMB 通過使用MB 近似技術，減少了計算復雜度，實現了比GGIW-PMBM更快的計算速度，二者在跟蹤精度上沒有明顯的差別。本文基于PMB濾波器，故而未與PMBM濾波器作對比。

為了驗證本文算法的性能，設計了兩組實驗。實驗1驗證了采用GPR-GGM模型對擴展目標建模后，PMB濾波算法在多擴展目標跟蹤中對擴展形狀估計效果的提升。實驗2驗證了提出的衍生目標模型及相應的GPRPMBS算法能夠檢測并跟蹤衍生目標。

4.1 算法性能評價指標

4.1.1 GOSPA距離

GOSPA（generalized optimal sub-pattern assignment）[28]是為了解決OSPA 距離中，若其中一組集合為空時，在相同的參數條件下，無論另一組集合內的元素如何變化，兩組集合的OSPA距離都相等的情況提出的。它通過在集合勢誤差內添加參數去計算得到與集合勢誤差不同的位置誤差，去除了OSPA 距離的歸一化，也可以說GOSPA距離是OSPA距離非歸一化的表現形式，它通過計算得到集合間所有距離之和，它的值會隨著真實值和估計值距離的增大而增大，對于計算集合勢誤差有一定范圍的縮放比例。

當c ＞0,p≥1，且集合勢誤差歸一化參數α滿足0 ≤α≤2 時，GOSPA距離可以表示為：

式中，隨機有限集合X和Y分別表示X={x1,x2,…,xn}和Y={y1,y2,…,yn},|X|和 |Y|分別表示集合X和Y內元素的總個數，π表示集合Y內所有元素的可能排列情況。

當α=2 時的GOSPA距離可以看作由定位誤差、虛警誤差和漏檢誤差三部分組成[28]。

4.1.2 IOU

IOU體現了算法對目標形狀估計的精確度，假設R和分別是為目標的真實形狀和估計的形狀，IOU的計算方法如下：

4.2 仿真分析與比較

4.2.1 實驗1

實驗設定[-400，400]×[400，400]內為監控區域，在監控區域內有三個不同形狀的擴展目標，實驗中假設目標形狀不變化。目標真實運動軌跡如圖1所示。

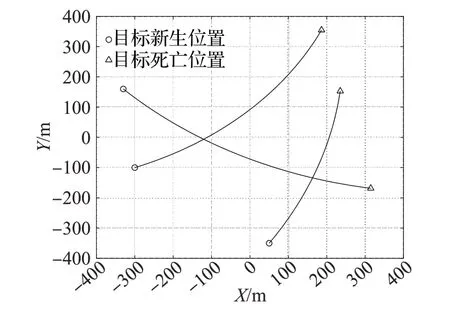
圖1 目標真實軌跡（實驗1）Fig.1 Target real trajectories（Experiment 1）

目標運動遵循勻轉彎運動模型。運動狀態轉移矩陣、過程噪聲協方差矩陣、擴展狀態轉移矩陣及其噪聲協方差矩陣分別為：

其中，采樣時間T=1 s，ω為勻轉彎速度，整個跟蹤時長為50 s。過程噪聲方差1，形狀動態參數α=0.000 1。高斯過程回歸模型采樣點數M=50，k(θ,θ)為GP協方差函數。

目標1 是長軸為4 m，短軸為3 m 的十字形目標，初始狀態為[-300;-100;0;13;5;ω]；目標2是長軸為5 m，短軸為3 m 的橢圓目標，初始狀態[-330;160;0;13;-13;ω]；目標3 是長為6 m，寬為4 m 的矩形目標，初始狀態[50;-350;0;10;15;ω]。目標量測率設置為20，跟蹤區域雜波率為8，量測噪聲協方差R=0.01*I2。目標的存活概率和檢測概率分別為pS=0.99,pD=0.98 。GOSPA參數為p=2,c=5。

實驗1 將本文提出的基于高斯過程回歸的泊松多伯努利（GPR-PMB）算法與GGIW-PMB 算法進行比較，對比分析了二者在多擴展目標跟蹤中的性能。表1 是GPR-PMB 和GGIW-PMB 算法的運行時間。從表中可以看出，GPR-PMB算法相比GGIW-PMB算法的運行時間要長，因為高斯過程回歸模型的引入使得GPR-PMB算法的時間復雜度要高于GGIW-PMB算法。

表1 GPR-PMB和GGIW-PMB算法的運行時間Table 1 Running time of GPR-PMB and GGIW-PMB

圖2 是實驗仿真得到的多目標運動軌跡局部放大圖。從圖中可以看出，基于隨機矩陣的GGIW-PMB 算法只能將目標擴展形狀近似為橢圓，而高斯過程回歸可以更為精確地估計出目標的輪廓。

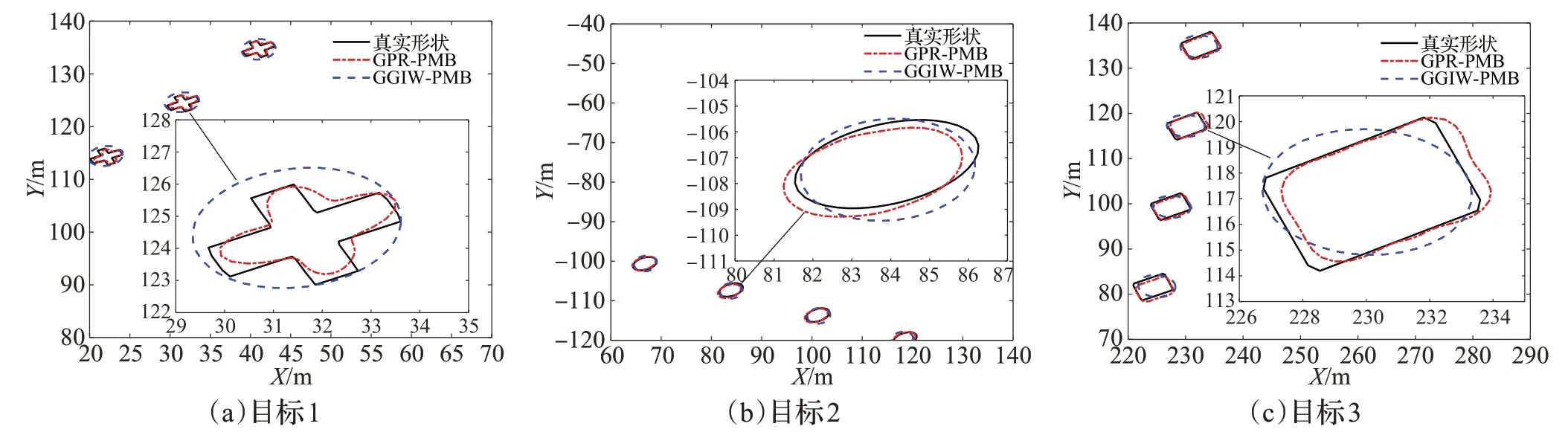
圖2 估計形狀與真實形狀對比圖Fig.2 Estimated shape versus real shape

圖3 是將三個目標擴展狀態估計結果與真實擴展狀態進行對比計算得到的IOU圖。從圖3中不難看出，所提算法能夠跟蹤不同形狀的目標，且估計的擴展形狀能較好地反映目標的真實幾何形狀信息。采用高斯過程回歸量測模型對目標形狀進行建模，能對目標形狀做出更準確的估計，從而得到更精確的運動狀態估計結果。

圖3 IOU對比圖Fig.3 IOU comparison diagram

圖4是GPR-PMB算法和GGIW-PMB算法的GOSPA對比圖。從圖中可以看出，少數時刻GPR-PMB 算法與GGIW-PMB 算法的GOSPA 距離相同，多數時刻GPRPMB 算法的GOSPA 距離優于GGIW-PMB 算法。從上述實驗結果中可以看出，本文所提GPR-PMB 算法相比于GGIW-PMB 算法盡管運算復雜度有所增加，但對目標的運動狀態和擴展狀態的估計效果都有所提升。

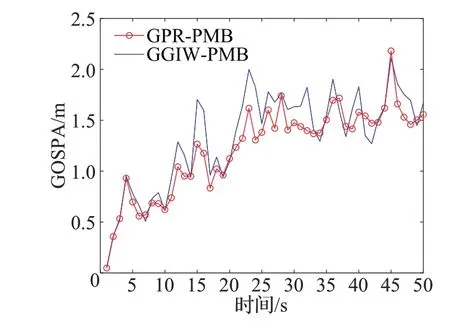
圖4 GOSPA對比圖Fig.4 GOSPA comparison diagram

4.2.2 實驗2

本文提出了新的衍生目標模型，實驗2設定衍生場景來驗證所提衍生目標模型的有效性。本實驗仍采用實驗1 的運動模型，但設定了衍生場景：假定目標1 在25 s 時刻發生衍生，衍生得到長軸為0.75 m，短軸為0.25 m的橢圓目標，記為目標4；假定目標2在32 s時刻發生衍生，衍生得到長為2.50 m，寬為1.25 m 的矩形目標，記為目標5。目標真實軌跡如圖5所示。

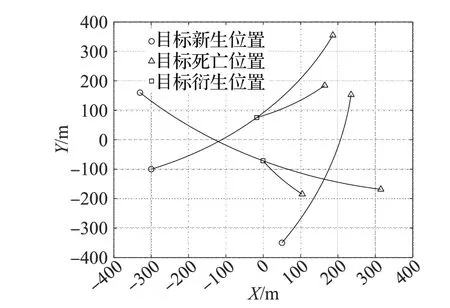
圖5 目標真實軌跡（實驗2）Fig.5 Target real trajectories（Experiment 2）

實驗2 將本文算法與GGIW-PMB 算法及不含衍生模型的GPR-PMB 算法進行比較，對比分析了三者在含衍生情況的多擴展目標跟蹤中的性能。圖6 為三種算法跟蹤過程中每一時刻估計的目標數。0～25 s期間，三種算法估計的目標數相同，都能正確地給出真實目標數；第一個衍生目標在25 s 時刻出現，第二個衍生目標在32 s時刻出現，從26 s及之后時刻三種算法的估計目標數中可以看出，采用了衍生模型的GPR-PMBS 能夠在衍生發生的下一時刻跟蹤到衍生目標，而GGIWPMB 算法和不含衍生模型的GPR-PMB 算法無法檢測并跟蹤衍生目標。

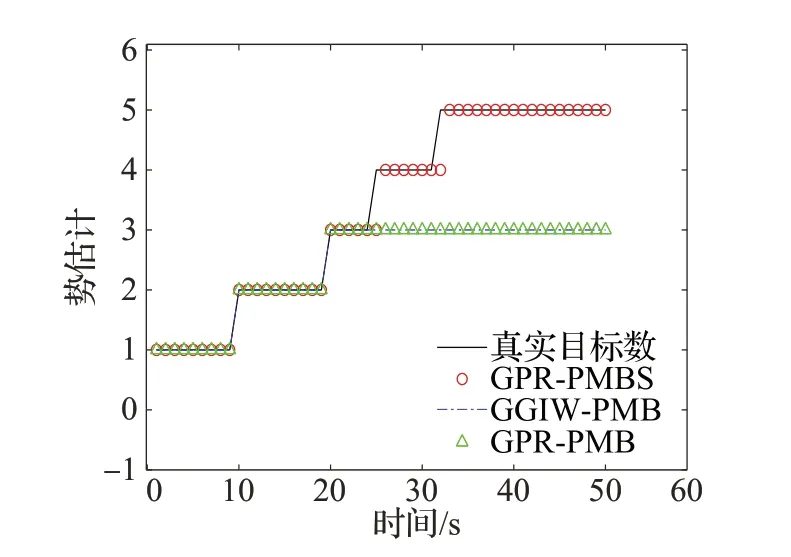
圖6 勢估計對比圖Fig.6 Comparison diagram of cardinality estimations

5 結論

本文研究了PMB擴展目標跟蹤算法中的非橢圓擴展目標形狀估計問題，引入GPR，通過擴展卡爾曼技術實現GPR 的遞歸，得到了可用于非橢圓擴展目標建模的GPR-GGM模型。在此基礎上，研究了衍生目標跟蹤問題，結合提出的衍生模型，得到了一種能跟蹤不同形狀擴展目標和衍生目標的GPR-PMBS算法。該算法采用GPR-GGM模型對擴展目標進行建模，并結合提出的衍生模型，能實現對含衍生目標的不同形狀擴展目標進行跟蹤，仿真結果驗證了本文算法的有效性。