GeoGebra在高中數學中的應用
居加穎


摘 要:GeoGebra可以呈現形象、生動的數學圖象,能夠充分調動學生的視覺感受,提升學生空間想象能力,從而促進學生數學形象思維發展.在教學中,要注重學生為主體,增加互動性,注重適切性,落實核心素養,并注重多元評價.師生進行深入研究,豐富教學的內容,拓展學生學習方式,改善學生認知能力,發展學生的數學學力,讓數學的教學向縱深推進.
關鍵詞:GeoGebra;高中數學;超越函數
1 提出問題
在高三的函數、導數教學中,存在著一些問題:(1) 學生自主學習能力不強,畏難情緒較大.由于函數、導數的知識本身比較抽象,學生在高一、高二學習時比較吃力,做題的正確率不高.并且,自我反思總結不足,大部分學生學習函數、導數的積極性不高,對函數、導數的內容產生懼怕、排斥心理.(2) 函數圖象掌握不夠扎實,尤其超越函數.超越函數,指的是變量之間的關系不能用有限次加、減、乘、除、乘方、開方運算表示的函數.三角函數、指數函數、對數函數等,都屬于超越函數.學生雖然到了高三,但畫圖能力還比較薄弱,尤其對超越函數的圖象掌握不好,作圖比較不嚴謹、不規范,經常想當然就把圖畫出來了,這樣錯誤的圖象會導致錯誤的結果.(3) 數形結合思想意識不夠,有待加強.數形結合思想體現了對數學問題的抽象與直觀的轉化,數形結合是對問題的本質內涵的邏輯揭示,也是對問題的直觀認識,但學生的數形結合意識還不夠強.(4) 函數、導數教學中使用信息技術,尤其GeoGebra較少.目前,大多數教師在教學中,遇到函數、導數問題時,會直接根據單調性等畫出函數圖象,學生使用GeoGebra研究函數、導數的參與度不高,信息技術與高三數學教學整合的優勢不能充分展現.
2 GeoGebra應用于函數教學的優勢
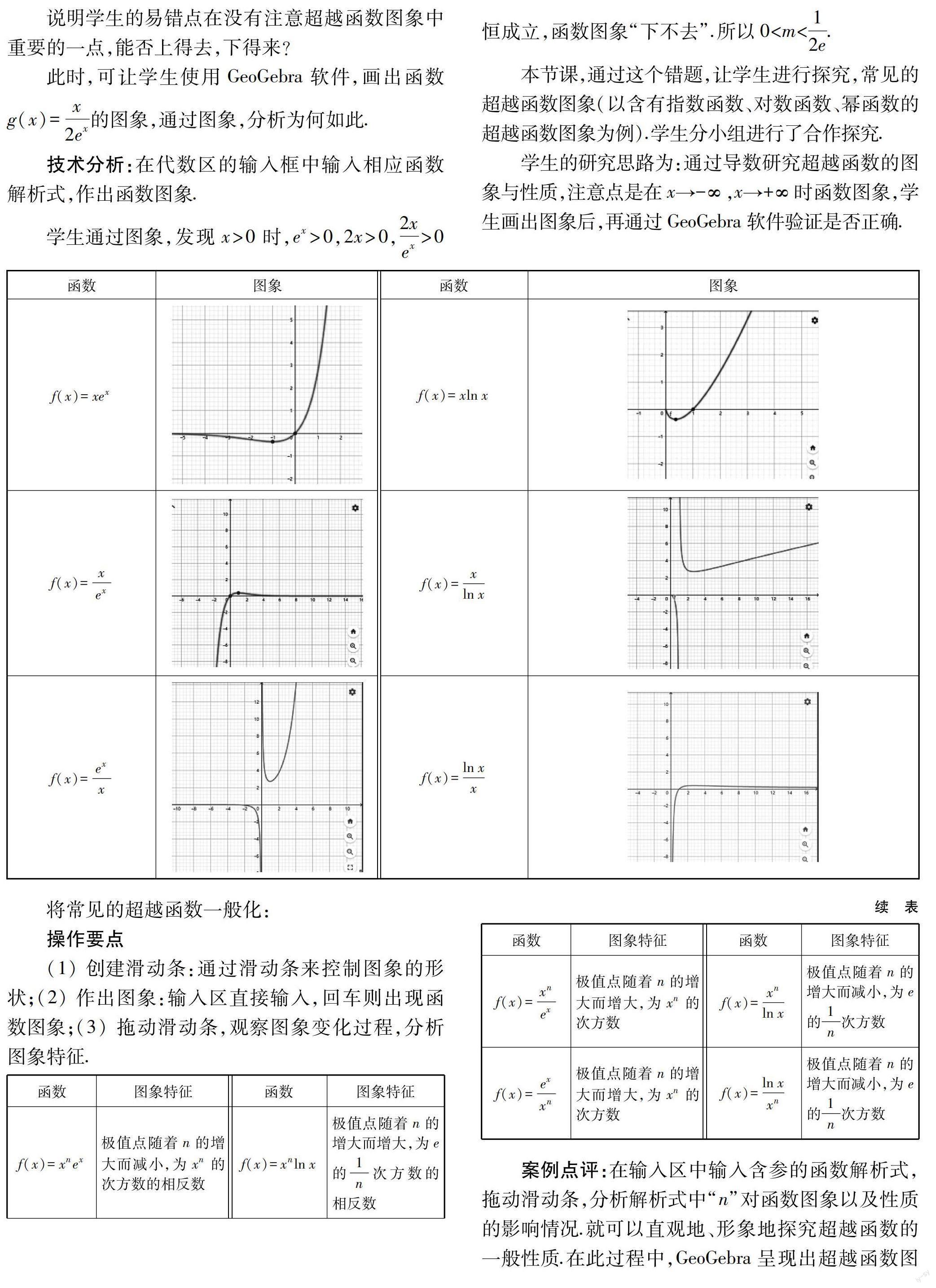
GeoGebra的功能區域有代數區、幾何區、數據表區.對大多數教師和學生而言,利用GeoGebra研究函數圖象,通過簡單學習即可操作.只要在輸入欄中輸入表達式,在代數區就會出現表達式,同時,在幾何區域就會出現圖形.幾何區與代數區的內容是聯動的,相互關聯.GeoGebra中的滑動條,可以控制函數中參數變化對圖象的影響,直觀地展現出圖象變化情況,在此過程中,讓同學們更加直觀地觀察,進行函數圖象與性質的探究,動態展示形與數的特征變化,克服了傳統教學的抽象性.
3 案例
探究后測的兩個問題,年級均分均高于4分,充分說明通過深入探究,學生對數形結合的思想的理解與應用都得到了提高,同時,在此過程中,通過精確、動態、直觀的可視化形式,師生共同突破了重難點,增強了學生學習的自信心,發展了數學抽象、直觀想象等核心素養.
4 教學啟示
4.1 以學生為主體
GeoGebra輔助教學,并不是要將其作為高三數學課堂的重點,也不是要用GeoGebra替代傳統教學,而是讓教師通過GeoGebra的使用讓一些復雜的函數圖象、立體圖形、圓錐曲線等可視化、直觀化,有助于學生經歷知識的發生和發展的過程,理解數學知識的本質,進一步理解數學、應用數學,在探究、交流、總結的過程中,建構知識的完備性.從而真正做到以學生為主體,培養學生的探究精神,落實立德樹人的根本任務.
4.2 注重其適切性
利用GeoGebra呈現時,若能滯后,就不超前.比如,利用GeoGebra處理定值定點問題、立體幾何問題、函數圖象輔助分析等,這些都是GeoGebra的優勢,但是出現的時機一般建議滯后呈現,先用傳統的方法進行理性探究,再通過GeoGebra直觀展示,不可本末倒置.此外,教師不能重GeoGebra而輕教學設計,要以教學設計為主,信息技術為輔,一堂好課的打磨,永遠是把教學設計放在第一位,設計得好,才能銜接自然,引人入勝,揭露本質.信息技術只能是錦上添花.教師了解學生的課堂表現、數學思維發展情況,從而改進教學行為,促進深度學習,發展學生的數學學力,讓數學的教學向縱深推進[1].
4.3 核心素養落地
教學過程中,通過探究“n”對函數圖象以及性質的影響情況、探究后測兩個問題,增加師生互動,學生進行深入研究,讓數學走進學生思維深處,促進學生對數學本質的認識,使其保持高水平思維參與課堂,增強對數學思想方法感悟,并發展了學生數學抽象、直觀想象、邏輯推理等核心素養.
參考文獻:
[1] 羅建宇.從融合到創新:基于GeoGebra的數學深度學習[J].數學通報,2020(2):23-26.

