面向耦合系統的交替方向滾動時域電壓分層協同優化控制

楊 浩 蘇文棟 谷 毅 張 軒 郭東波 唱一鳴

（1.現代電力系統仿真控制與綠色電能新技術教育部重點實驗室（東北電力大學） 吉林 132012 2.國網遼寧省電力有限公司 沈陽 110006）

0 引言

我國北方地區風、光資源豐富，新能源裝機容量連續提高[1-4]，由風、光新能源場站與傳統火電機組構成并經外送通道功率送出的耦合系統普遍存在[5]。耦合系統在支撐我國能源轉型發展的同時，也因新能源功率的隨機波動特征導致潮流狀態復雜多變，電壓越限問題突出[6-9]。含多新能源場站的耦合系統規模龐大，電壓優化控制模型維度高，求解困難；不同場站運營商之間存在信息隱私壁壘，加劇了電壓控制難度。與此同時，耦合系統中新能源單元并網點（Points of Common Coupling,PCC）、場站并網點及功率外送并網點均對電壓安全提出了嚴格要求，使電壓控制難度與電壓安全要求之間的矛盾更加凸顯，亟須提出適用于耦合系統的電壓控制策略以提高電壓安全運行水平。

目前，電壓調控通常采用集中式和分散式控制結構。集中式控制中，控制中心通過收集電網電壓和無功信息，構建全局電壓優化模型并進行解算后下發控制指令至各無功源設備[10-15]。文獻[10]針對主動配電網電壓越限問題，提出了基于模型預測控制（Model Predictive Control, MPC）的電壓協調控制方法。文獻[11]面向交直流混聯系統，納入直流輸電換流器參與電壓控制，提出了基于靈敏度的電壓協調優化控制模型。文獻[12]考慮儲能對配電網電壓的調節，建立了針對全局電壓偏差響應控制的協調優化模型。文獻[13]在基于靈敏度的電網分區與關鍵節點選取基礎上，提出了采用粒子群優化的集中式電壓控制模型。文獻[14]提出了量測數據驅動的靈敏度計算方法，并據此建立了以綜合電壓控制偏差和控制代價最小為目標的電壓優化控制模型。文獻[15]對大量不同場景下的無功-電壓控制過程進行演員-評論家強化學習訓練，建立電網中無功控制量與電壓狀態間的映射關系，實現了電壓集中控制。以上集中式控制方法中，優化模型復雜程度及其計算負擔會隨著新能源接入規模的增大而顯著增加，并且依賴電網全局信息，隱私保護性差，對信息完備性和通信可靠性均提出了較高要求。

分散式控制結構中，各無功控制源僅利用本地電壓信息作出決策，無需相互協調，具有響應速度快、通信成本低的特點[16-18]。文獻[16]利用靈敏度建立了配電網光伏無功調控與電壓狀態間的映射模型，提出了一種基于本地信息的光伏無功-電壓自治控制規則。文獻[17]以“集中訓練，分散執行”框架進行強化學習策略生成，應用于主動配電網分散控制，實現無功控制資源本地電壓控制。文獻[18]利用混合式配電變壓器進行電壓控制，各變壓器基于本地電壓信息進行決策控制并通過在線時域修正，提高電壓安全水平。僅基于本地電壓信息進行決策的分散式控制，缺乏系統性優化，整體協調性能不足，電壓控制效果難以有效保障。

分布式電壓控制基于局域通信而非全局或本地通信來構建電壓控制策略，結合了集中式和分散式控制的優勢，近年來得到一定發展[19-23]。文獻[19]提出了一種基于多代理系統的主動配電網分布式電壓控制策略，以分布式形式實現對電壓的控制，并提高新能源消納水平。文獻[20-21]提出了利用交替方向乘子法（Alternating Direction Method of Multipliers,ADMM）的配電網分布式電壓控制，實現了各分區內電壓偏差控制。文獻[22]基于圖論法對配電網分區，各區域通過其局部控制中心進行光伏逆變器無功優化控制，相鄰區域間進行邊界信息交互，實現協同控制。文獻[23]提出了一種針對高比例新能源發電集群的分布式電壓控制方法，利用新能源發電單元間的信息交互實現分布式反饋電壓控制，減少電壓越限風險。分布式控制策略通過分解全局優化問題，利用邊界信息協調使系統達到最優控制的目的，降低了對通信能力和數據計算能力的要求，具備抗干擾性和隱私保護性等優點。

綜上所述，現有電壓控制策略均未針對耦合系統結構進行設計，本文結合耦合系統單元-場站-系統的物理層級特征，以新能源單元并網點、場站并網點及耦合系統功率外送并網點的電壓運行要求為控制目標，面向電壓時序過程控制，結合MPC 和ADMM，提出了一種綜合考慮系統運行網損優化和電壓校正控制的電壓分層分布協同控制策略。本文的主要創新點為：①提出了基于場站層與系統層分解的耦合系統電壓分層協同控制結構，將復雜的耦合系統全局電壓優化問題分解為多個子優化問題，降低了優化模型規模與求解難度；②同時計及電壓控制與網損優化，提出了MPC 和ADMM 相結合的網損優化與電壓校正自適應切換的滾動時域控制方法，實現場站層與系統層電壓協同控制的同時優化系統網損，提高運行經濟性。

1 耦合系統電壓分層協同控制架構

1.1 耦合系統電壓控制要求及無功資源

在同一電網區域內，風、光等多新能源場站與傳統同步發電機組構成并經外送通道功率送出的耦合系統如圖1 所示。圖中為我國北方某實際區域電網，Ⅰ為海上風電場，經D 點并網，Ⅱ為光伏站，經E、F 點并網，上層送端系統經并網點A 功率外送。該區域電網中新能源單元、新能源場站和耦合系統對外并網點均需滿足不同的并網電壓安全標準，耦合系統外送并網點允許電壓運行范圍為[0.99(pu),1.01(pu)]，新能源單元和新能源場站并網點電壓安全運行范圍為[0.97(pu), 1.07(pu)][24-25]。在響應耦合系統電壓控制的無功控制資源分布上，場站層包含具備電壓調控能力的新能源單元機組和場站并網點處加裝的靜止無功發生器（Static Var Generator, SVG）等無功補償設備，系統層包含同步發電機組、無功補償裝置等無功源設備。

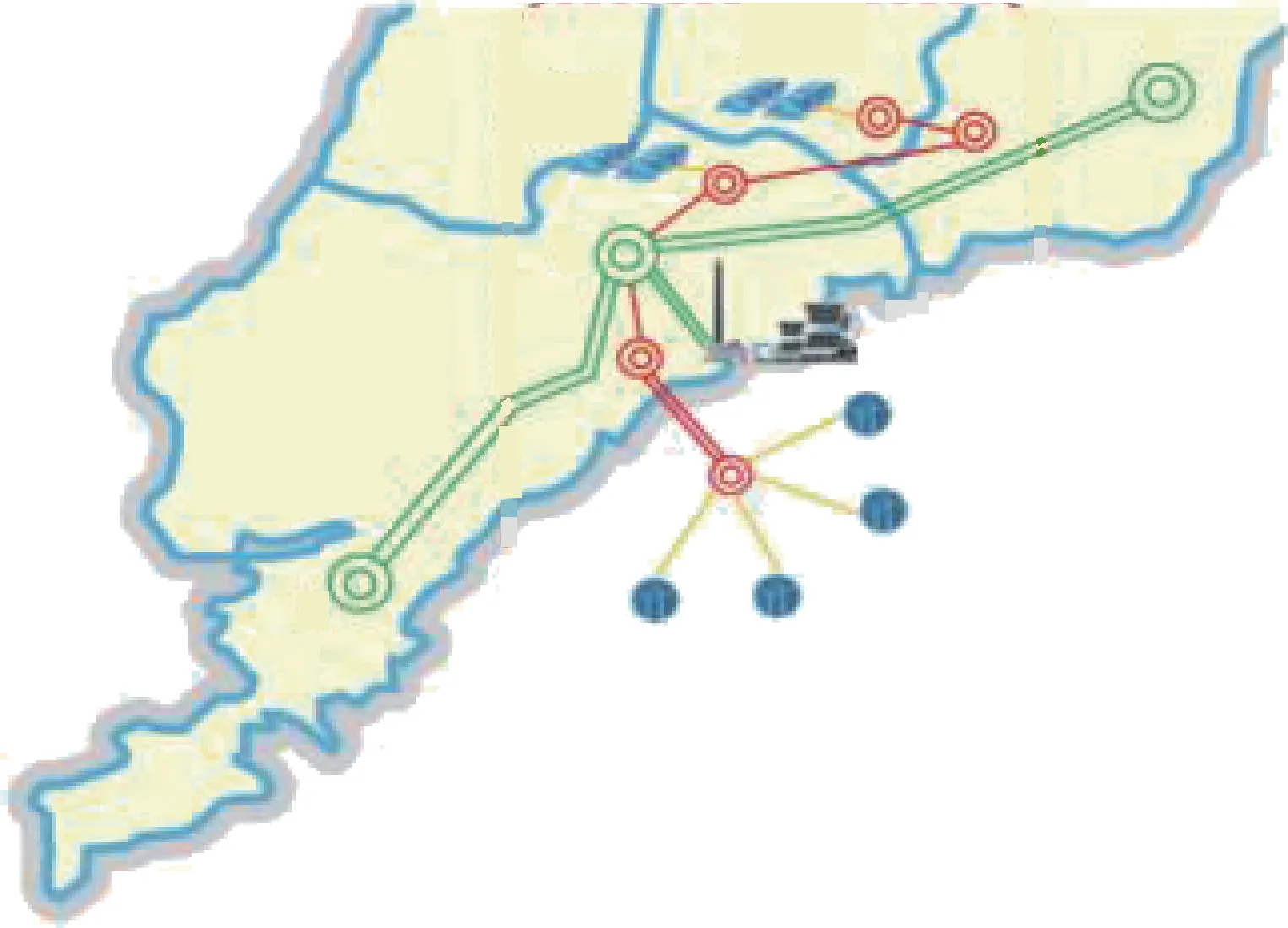
圖1 耦合系統Fig.1 Typical coupled system

1.2 耦合系統電壓分層協同控制結構

面對耦合系統各并網點電壓控制問題，考慮到其控制資源多、散和網絡拓撲結構復雜的特點，本文針對耦合系統的物理層級結構建立了分層電壓協同控制策略，以降低電壓優化模型規模與求解難度，并保護不同運營主體隱私性，所建立的控制結構如圖2 所示。圖中，將耦合系統分解為上層系統層和下層新能源場站層。系統層為承擔功率外輸送的高電壓等級網絡，場站層為由風/光新能源單元構成的低電壓等級網絡，系統層與場站層通過場站并網點互聯。系統層將所在層級的同步發電機、無功補償設備和整體風/光新能源場站作為可參與電壓調控的控制資源；場站層將場站內部的新能源單元和無功補償設備作為電壓控制資源。

圖2 電壓分層協同控制結構Fig.2 Structure of hierarchical coordinated voltage control

各層根據監測的關鍵節點（系統層：場站并網點、功率外送并網點，場站層：場站并網點、新能源單元并網點）電壓狀態，進行電壓校正與網損優化自適應切換控制，建立基于MPC 的滾動時域控制模型。結合ADMM 交替迭代方法，系統層與場站層間的協同控制過程為：系統層通過求解該層所建立的滾動時域控制模型，將得到的新能源場站并網點電壓作為參考電壓指令下發至場站層；場站層接受該控制指令，求解對應場站層的滾動時域控制模型，并將場站并網點電壓和無功可調控范圍傳遞至系統層；系統層再進行求解，進行交互迭代計算，直到達到系統層-場站層互聯的場站并網點電壓一致性，最終給出各無功控制設備的控制指令。

2 基于滾動時域的電壓分層控制模型

大規模新能源并網下，耦合系統中各并網點電壓隨著新能源出力波動性也呈現出強波動特征，電壓越限問題突出。面向時間過程的MPC 算法考慮系統未來運行狀態構建優化控制模型，進行模型滾動時域求解和狀態反饋校正，能夠有效地應對系統運行的不確定性，具備較強的控制魯棒性和可靠性。本節針對耦合系統的分層結構，基于MPC 分別對系統層和場站層建立相應的滾動時域控制模型。

2.1 系統層控制模型

2.1.1 系統層控制目標自適應切換

系統層控制模式根據功率外送并網點和新能源場站并網點電壓監測信息，自適應地切換為電壓校正或網損優化模式，當監測的節點電壓均滿足安全運行范圍時進行網損優化控制；否則，進行電壓校正控制。模式切換判斷表達式為

式中，Us為系統層功率外送并網點和新能源場站并網點的電壓向量；和分別為對應的節點電壓允許范圍上、下限；JH為系統層控制目標；為網損優化函數；為電壓校正函數。

2.1.2 系統層電壓校正控制

電壓校正控制時，基于MPC 時序控制特點，以控制時序（1～Nc）內電壓偏差和控制代價綜合最小作為目標函數，MPC 預測方程通過電壓靈敏度信息建立電壓序列預測模型，具體表達式為

式中，Cs,v1、Cs,v2分別為系統電壓偏差控制和控制代價權重系數，均大于0；k為預測控制窗口，k=1， 2,…,Nc；Us(k)為k時刻電壓向量；Us,ref為參考（期望的）電壓向量；Δxs(k)=[ΔUs,g(k) ΔQs,C(k) ΔQs,w(k)ΔQs,p(k)]T為系統層控制資源的調節量，其中ΔUs,g為同步機組機端電壓調節量，ΔQs,C為無功設備的無功調節量，ΔQs,w為風電場的無功調節量，ΔQs,p為光伏站的無功調節量；ΔPs(k)為新能源場站k時刻預測的有功輸出波動量；?Us/?xs為電壓與控制量的靈敏度矩陣；?Us/?Ps為電壓與新能源場站有功出力的靈敏度矩陣，用于計算預測控制窗口內的電壓預測值。

2.1.3 系統層網損優化控制

網損優化控制時，構建基于MPC 的綜合網損和控制代價的時序優化控制目標函數，并通過網損靈敏度信息建立網損序列的預測模型。

式中，Cs,L1、Cs,L2分別為網損和控制代價權重系數，均大于零；Ps,Loss(k)為k時刻系統網損；?Ps,Loss/?xs為網損與控制量間的靈敏度矩陣；?Ps,Loss/?Ps為網損與新能源場站有功的靈敏度矩陣，用以得到網損預測值。以上構建模型中所需要的靈敏度矩陣可基于系統層潮流計算，采用攝動法或雅可比矩陣求逆獲取。

2.1.4 系統層運行控制約束

系統層在優化控制中需滿足如下約束條件

式中，Us,g(k)為同步機組k時刻端電壓；分別為同步機組機端電壓允許范圍上、下限；Qs,C(k)為無功補償設備k時刻無功輸出量；和分別為無功補償設備無功允許范圍上、下限；Qw(k)為風電場k時刻無功輸出量；(k)和(k)分別為風電場k時刻所能提供的無功輸出量范圍上、下限；Qp(k)為光伏站k時刻無功輸出量；(k)和(k)分別為光伏站k時刻所能提供的無功輸出量范圍上、下限。

2.2 場站層控制模型

2.2.1 場站層控制目標自適應切換

根據新能源場站為風電場或光伏站進行分別描述如下。

1）風電場切換

式中，Uw為風電場的場站并網點和風機單元并網點電壓向量；和分別為對應的節點電壓允許范圍上、下限；為風電場控制目標；為風電場的網損優化函數；為風電場的電壓校正函數。

2）光伏站切換

式中，Up為光伏站的場站并網點和光伏單元并網點的電壓向量；分別為對應節點電壓允許范圍上、下限；為光伏站控制目標；為光伏站網損優化函數為光伏站電壓校正函數。

2.2.2 場站層電壓校正控制

在新能源場站內，電壓校正控制時，綜合電壓偏差和控制代價的控制目標，表達式分別描述如下。

1）風電場

式中，Cw,v1、Cw,v2分別為風電場電壓偏差控制和控制代價權重系數，均大于零；Uw(k)為風電場k時刻電壓向量；Uw.ref為風電場參考（期望的）電壓向量；Δxw(k)=[ΔQw(k) ΔQw,C(k)]T為風電場k時刻內部控制資源的調節量，其中ΔQw為風機單元無功調節量，Qw,C為風電場無功控制設備的無功調節量；ΔPw(k)為風機單元k時刻預測的有功輸出波動量；?Uw/?xw為風電場電壓與控制量間的靈敏度矩陣；?Uw/?Pw為風電場電壓與風機單元有功的靈敏度矩陣。

2）光伏站

式中，Cp,v1、Cp,v2分別為光伏站電壓偏差控制和控制代價權重系數，均大于零；Up(k)為光伏站k時刻電壓向量；Up.ref為光伏站參考（期望的）電壓向量；Δxp(k)=[ΔQp(k) ΔQp,C(k)]T為光伏站k時刻內部控制資源的調節量，其中Qp為光伏站單元機組無功調節量，Qp,C為光伏站無功控制設備的無功調節量；ΔPp(k)為光伏單元k時刻預測的有功輸出波動量；?Up/?xp為光伏站電壓與控制量的靈敏度矩陣；?Up/?Pp為光伏站電壓與光伏單元有功靈敏度矩陣。

2.2.3 場站層網損優化控制

在新能源電站內，網損優化控制時，綜合網損和控制代價的控制目標，表達式分別描述如下。

1）風電場

式中，Cw,L1、Cw,L2分別為風電場網損和控制代價權重系數，均大于零；Pw,Loss(k)為風電場k時刻的網損；?Pw,Loss/?xw為風電場網損與控制量間的靈敏度矩陣；?Pw,Loss/?Pw為風電場網損與風機單元有功的靈敏度矩陣。

2）光伏站

式中，Cp,L1、Cp,L2分別為光伏站網損和控制代價權重系數，均大于零；Pp,Loss(k)為光伏站k時刻的網損；?Pp,Loss/?xp為光伏站網損與控制量間的靈敏度矩陣；?Pp,Loss/?Pp為光伏站網損與光伏單元有功的靈敏度矩陣。以上模型中靈敏度矩陣可基于新能源場站內部潮流計算，采用攝動法或雅可比矩陣求逆獲取。

2.2.4 場站層控制模型約束

求解上述目標函數均需要滿足新能源場站的運行約束條件。

式中，UL(k)為新能源場站的場站并網點和新能源單元并網點k時刻的電壓向量；UmaxL和UminL分別為對應節點電壓允許范圍上、下限；QL(k)為新能源單元k時刻的無功輸出量；QmaxL(k)和QminL(k)分別為對應單元k時刻的無功輸出量允許范圍上、下限；QC(k)為新能源場站中無功控制設備k時刻的無功輸出量；QmaxC和QminC分別為對應無功控制設備k時刻的無功輸出量允許范圍上、下限。

式（17）中QminL和QmaxL分別表示為

式中，SL為新能源場站中單元機組的容量；PL(k)為新能源場站單元機組在k時刻的有功輸出。

以上構建的電壓控制和網損優化控制均是基于MPC 面向未來時序控制進行的，其中未來時序電壓和網損均由相應靈敏度信息建立模型預測方程來預測獲取，通過求解優化模型得到控制的動作序列，施加第一個序列動作，并隨時間滾動重復進行。

3 基于ADMM 的耦合系統分層電壓控制模型求解

第2 節介紹了耦合系統分層控制框架下，系統層和場站層的控制模型。本節基于ADMM 方法分別對系統層和場站層進行分布式迭代求解，僅通過層級之間的關口（場站并網點）電壓信息一致性進行相互協調，實現電壓分層分布式控制。

3.1 基于ADMM 的控制模型增廣拉格朗日函數

面向系統層-場站層的分布式電壓控制框架中，各層以新能源場站并網點為共有節點，最終在迭代結束后節點電壓需達到一致，有

結合一致性約束，通過ADMM 算法將系統層和場站層的控制目標函數整合為以全局控制為目標的增廣拉格朗日函數Ψ，如式（20）所示，并基于對偶問題求解原理，對系統層-場站層電壓協同控制問題進行分解求解，如式（21）所示。

3.2 系統層分布式控制模型

系統層內，基于對偶問題分解原理，將式（20）中場站層控制量、拉格朗日系數和懲罰因子作為常數，得到分解模型中系統層分布式控制模型為

在求解過程中需要滿足式（6）約束，其中新能源場站可提供無功范圍Qminw、Qmaxw和Qminp、Qmaxp分別表示為

式中，Sw,i為風機單元容量；Pw,i(k)為風機單元k時刻有功輸出量；Qmaxw,C和Qminw,C分別為風電場中無功補償設備的無功調節范圍上、下限；Sp,j為光伏單元容量；Pp,j(k)為光伏單元k時刻有功輸出量；Qmaxp,C和Qminp,C分別為光伏站中無功補償設備的無功調節范圍上、下限。

3.3 場站層分布式控制模型

場站層內，基于對偶問題分解原理，將式（20）常數，得到分解模型中場站層分布式控制模型為

求解上述目標函數需要滿足系統的運行約束條件式（17）和式（18）。基于該約束求解場站層分布式控制模型，可得到場站層控制為目標的各新能源場站并網點電壓。

3.4 拉格朗日系數更新

在對拉格朗日系數更新時，基于對偶問題分解原理，將式（20）中系統層控制量、場站層控制量和懲罰因子作為常數，得到分解模型中拉格朗日更新式為

3.5 ADMM 迭代求解流程

本文采用電壓分層控制框架，并通過ADMM 算法進行迭代求解實現協同。為了加快求解迭代過程并提高求解收斂性，在ADMM 算法中采用自適應懲罰參數，具體步驟如下所示：

1）初始化ADMM 算法參數及系統內部各控制變量，設置算法迭代標識m=0。

2）更新迭代次數m=m+1。求解系統層分布式控制模型式（22），將各新能源場站并網點電壓值UH,(m+1)wp作為各場站并網點參考電壓指令傳遞至對應場站層控制系統。

3）求解場站層控制模型式（24），將各新能源場站并網點電壓值UL,(m+1)wp與場站所能提供的無功輸出范圍上、下限上傳至系統層。

4）采用梯度下降法求解式（25）對拉格朗日系數更新，得到

式中，d(m)為m次迭代時，系數的更新步長。

式中，μ和σ為懲罰因子更新參數；max[·]表示取矩陣或向量中的最大元素。

6）根據式（30）判斷是否滿足收斂條件，若滿足，則輸出步驟2）和步驟3）所求MPC 序列；否則返回步驟2）繼續迭代求解。

式中，r(m+1)為m+1 次迭代下原始殘差向量；s(m+1)為m+1 次迭代下對偶殘差向量；εpri和εdual分別為原始殘差和對偶殘差的收斂精度。

4 仿真分析

本文分別在修改的IEEE-14 節點耦合系統和大連某區域耦合系統上進行仿真計算，驗證本文所提出的交替方向滾動時域電壓分層協同優化控制的有效性和適用性。仿真計算基于Matlab R2022a 平臺，采用Yalmip-R2020 建模并調用商業求解器Cplex 12.10.0 求解。

4.1 修改的IEEE-14 節點耦合系統

修改后的IEEE-14 節點耦合系統如圖3 所示。分層結構中，系統層節點包括{1, 2,…, 14, 33, 34}，其中，節點集合{1, 2,…,14}為原系統節點，節點33和34 為功率外送節點，節點3 和14 分別為風電場和光伏站并網點。場站層節點集合為{15, 16,…, 32}，其中，節點集合{15, 16,…, 23}為風電場，節點15 裝設SVG；節點集合{24, 25,…, 32}為光伏站，節點24裝設 SVG。日內光伏站和風電場功率輸出波動與系統負荷波動參考比利時地區2023 年3 月7 日數據[26-28]設置，如圖4 所示。耦合系統并網點電壓允許范圍為[0.99(pu), 1.01(pu)]，其參考電壓取中間值1.0(pu)；按照新能源并網電壓要求，新能源場站及單元并網點電壓允許范圍為[0.97(pu), 1.07(pu)]，其參考電壓取中間值1.02(pu)。設備參數見附表1～附表3，算法初始參數和收斂參數分別見附表4 和附表5。本文MPC 面向日內在線電壓控制，控制步長為5 min，預測控制窗口為15 min。關于MPC 目標函數中的權重系數設置，為確保電壓校正和網損優化的控制效果，其中電壓偏差部分/網損優化部分的權重系數遠大于控制代價部分的權重系數，電壓校正控制過程中電壓偏差部分權重與控制代價權重比值取為100:1，網損優化控制過程網損部分權重與控制代價權重取值為10:1，見附表6。本文控制策略控制下無功源控制量如附圖1 和附圖2所示；算法原始殘差和對偶殘差收斂結果如附圖3所示。

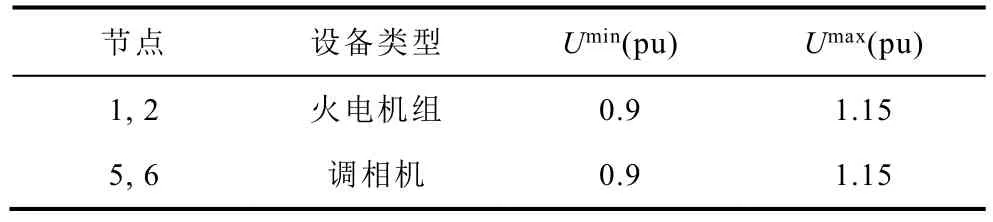
附表1 修改的IEEE-14 節點耦合系統中無功控制設備參數App.Tab.1 Parameters of reactive power equipment in the modified IEEE-14 coupled system

附表2 修改的IEEE-14 節點耦合系統中新能源參數App.Tab.2 Parameters of new energy in the modified IEEE-14 coupled system

附表3 修改的IEEE-14 節點耦合系統中SVG 參數App.Tab.3 Parameters of SVG in the modified IEEE-14 coupled system

附表4 修改的IEEE-14 節點耦合系統中ADMM 算法初始參數設置App.Tab.4 Initial setting parameters of ADMM in the modified IEEE-14 coupled system

附表5 修改的IEEE-14 節點耦合系統中ADMM 算法收斂參數設置App.Tab.5 ADMM convergence parameters in the modified IEEE-14 coupled system

附表6 修改的IEEE-14 節點耦合系統中MPC 模型權重設置App.Tab.6 Weight parameters in MPC model in the modified IEEE-14 coupled system

圖3 修改后的IEEE-14 節點耦合系統Fig.3 Modified IEEE 14 coupled system

圖4 修改后IEEE-14 節點耦合系統功率波動Fig.4 Power fluctuation in the modified IEEE-14 coupled system

圖5 為該耦合系統未考慮電壓控制時，各并網點的電壓波動情況，在新能源功率和負荷功率共同作用下，新能源單元、場站和耦合系統并網點出現了電壓越上限和越下限問題。由圖5 可知，系統在負荷較低、新能源有功輸出較高時線路出現逆潮流現象，電壓越上限；在負荷高峰，新能源有功輸出較低時，電壓越下限。

圖5 無控制IEEE-14 節點耦合系統各并網點電壓波動情況Fig.5 PCC voltage without control in the modified IEEE-14 coupled system

針對上述功率波動場景下并網點電壓越限問題，考慮以下三種基于MPC 的電壓控制方式：

1）分布協同控制，即為針對耦合系統的分層結構，前文所建立的綜合考慮系統運行網損優化和電壓校正雙模式自適應切換的電壓分層分布式協同控制策略。

2）分散控制，系統層和新能源場站層以各自層級內的并網點電壓校正和網損優化為控制目標，并進行電壓校正控制和網損優化控制模型自適應切換，系統層與新能源場站層之間無直接信息交互，各層級進行電壓校正控制/網損優化控制的分散式控制。

3）穩壓控制，系統層和場站層均針對電壓校正進行控制而不考慮網損優化，系統層外送并網點電壓控制參考值為1.0(pu)，場站層和新能源單元并網點電壓控制參考值為1.02(pu)，只進行系統層和場站層的電壓偏差校正控制，同時考慮了系統層與場站層間分布式協調。

實施上述三種控制策略后，控制效果分別如圖6～圖8 所示。控制效果評判所遵循的原則為：在并網點電壓校正控制滿足其上下限安全范圍要求時，電網運行網損越小，控制效果越優。從圖6 可看出，在分布協同控制下，考慮全天內功率波動情況，耦合系統并網點節點33 和34 的電壓有效控制在要求范圍[0.99(pu), 1.01(pu)]內，風電場和光伏站的并網節點 3 和節點 14 電壓控制在允許范圍[0.97(pu), 1.07(pu)]內，且風機單元和光伏單元并網點電壓均滿足安全范圍要求。如圖7 所示在分散控制策略下，耦合系統并網點電壓未能滿足規定的電壓范圍要求，存在嚴重的電壓越限問題，新能源場站和單元并網點電壓基本可滿足安全要求。在圖8所示的穩壓控制策略下，控制模型以電壓偏差最小為目標，新能源單元和場站并網點電壓控制在參考電壓1.02(pu)近鄰域，耦合系統并網點電壓控制在參考電壓1.0(pu)近鄰域，滿足電壓安全控制要求。整體來看，分布協同控制和穩壓控制策略可有效應對耦合系統功率波動所造成的電壓越限問題。以上仿真中關于迭代信息和控制量變化，參考附圖1～附圖3。

圖6 分布協同控制下IEEE-14 節點耦合系統各并網點電壓運行結果Fig.6 PCC voltage with distributed coordinated voltage control in the IEEE-14 coupled system

圖7 分散控制下IEEE-14 節點耦合系統各并網點電壓運行結果Fig.7 PCC voltage with decentralized control in the modified IEEE-14 coupled system

圖8 穩壓控制下IEEE-14 節點耦合系統各并網點電壓運行結果Fig.8 PCC voltage with constant voltage control in the IEEE-14 coupled system

上述三種控制策略下的耦合系統日平均網損對比如圖9 所示。穩壓控制策略下，以電壓偏差最小為控制目標，未充分考慮電網運行經濟情況，在電壓偏差較大時，通過調用大量無功控制資源對電壓進行校正，導致系統運行網損高，日平均網損為28.18 MW；分散控制下，因同時計及電壓和網損控制，耦合系統網損水平下降，日平均網損為25.98 MW，但在控制過程中層級間缺乏信息交互，未能從整體上進行協調以充分降低系統網損；分布協同控制下，通過系統層與場站層間信息交互，整體協調無功控制資源，實現在滿足各類并網點電壓運行安全要求時，降低了系統運行網損，日平均網損為22.84 MW，提高了運行經濟性。

圖9 不同控制方式下IEEE-14 節點耦合系統網損Fig.9 Network loss of IEEE-14 coupled system considering different control strategies

4.2 大連某區域電網

以大連某區域新能源與傳統電源耦合并網系統為例進一步驗證本文所提控制策略的有效性。該區域電網包括20 kV 火電機組400 MW、0.7 kV 風電450 MW 和0.4 kV 光伏450 MW，呈現為高比例新能源區域電網。系統結構如圖10 所示，其中，系統層節點集合為{1, 2,…, 12, 127}，節點1 為功率外送節點，節點10 和11 分別為風電場和光伏站并網點。場站層節點集合為{13, 14,…, 126}，其中，節點集合{13, 14,…, 63}為風電場，節點10 裝設SVG，節點集合{64, 65,…, 126}為光伏站，節點11 裝設SVG。同樣參考比利時地區功率日波動情況，系統日內光伏站和風電場功率輸出波動與系統負荷波動情況如圖11 所示。系統內其他元件參數見附表7～附表9，算法初始參數和收斂參數見附表10～附表12，本文分布協同控制下各無功控制資源控制量如附圖4 和附圖5 所示，算法原始殘差和對偶殘差收斂結果如附圖6 所示。

附表7 大連耦合系統中無功控制設備參數App.Tab.7 Parameters of reactive power equipment in Dalian coupled system

附表8 大連耦合系統中新能源參數App.Tab.8 Parameters of new energy in Dalian coupled system

附表9 大連耦合系統中SVG 參數App.Tab.9 Parameters of SVG in Dalian coupled system

附表10 大連耦合系統中ADMM 算法初始參數設置App.Tab.10 Initial setting parameters of ADMM in Dalian coupled system

附表11 大連耦合系統中ADMM 算法收斂參數設置App.Tab.11 ADMM convergence parameters in Dalian coupled system

附表12 大連耦合系統中MPC 模型權重設置App.Tab.12 Weight parameters in the MPC model in Dalian coupled system

圖10 大連某局域耦合系統Fig.10 A coupled system in Dalian

圖11 大連某局域耦合系統功率波動Fig.11 Power fluctuation in the coupled Dalian system

圖12 為該耦合系統在新能源功率和負荷功率波動共同作用下，新能源單元、場站和系統并網點全天電壓演變狀態。在時段0:00—5:30、20:00—21:30 風機出力較大時，耦合系統功率外送并網點和風電場單元均出現電壓越上限問題，在時段12:00—15:00 光伏有功出力較大時，耦合系統功率外送并網點和光伏站單元出現電壓越上限問題，在時段07:30—10:45和 17:15—18:45 耦合系統功率外送并網點出現電壓越下限問題，需針對上述問題進行控制。

圖12 無控制時大連某局域耦合系統各并網點電壓Fig.12 PCC voltage without control in the coupled Dalian power system

實施4.1 節所提的分布協同控制、分散控制和穩壓控制策略后，該耦合系統各類并網點電壓分別如圖13～圖15 所示，耦合系統平均網損如圖16 所示。在分布協同控制和穩壓控制下，耦合系統功率外送并網點、新能源場站并網點和新能源單元并網點電壓均能夠有效控制在安全范圍內，而分散式控制下耦合系統功率外送并網點和風機單元并網點均出現了嚴重電壓越限問題。對比網損變化情況，分布協同控制下耦合系統的平均網損最小，為20.52 MW；分散控制時系統平均網損為25.34 MW；穩壓控制時平均網損最大，為27.36 MW。從以上耦合系統電壓控制效果和運行網損可充分看出，所提分層協同電壓優化控制策略能夠滿足各類并網點電壓允許的安全范圍，并使得系統運行網損最小，提高了系統電壓安全性和運行經濟性。上述仿真計算中關于交互迭代信息和控制量的變化如附圖4～附圖6 所示。

圖13 分布協同控制下大連耦合系統各并網點電壓Fig13 PCC voltage flucatuation of in the Dalian coupled system with cooperative optimization control

圖14 分散控制下大連耦合系統各并網點電壓Fig14 PCC voltage in the Dalian coupled system with decentralized control

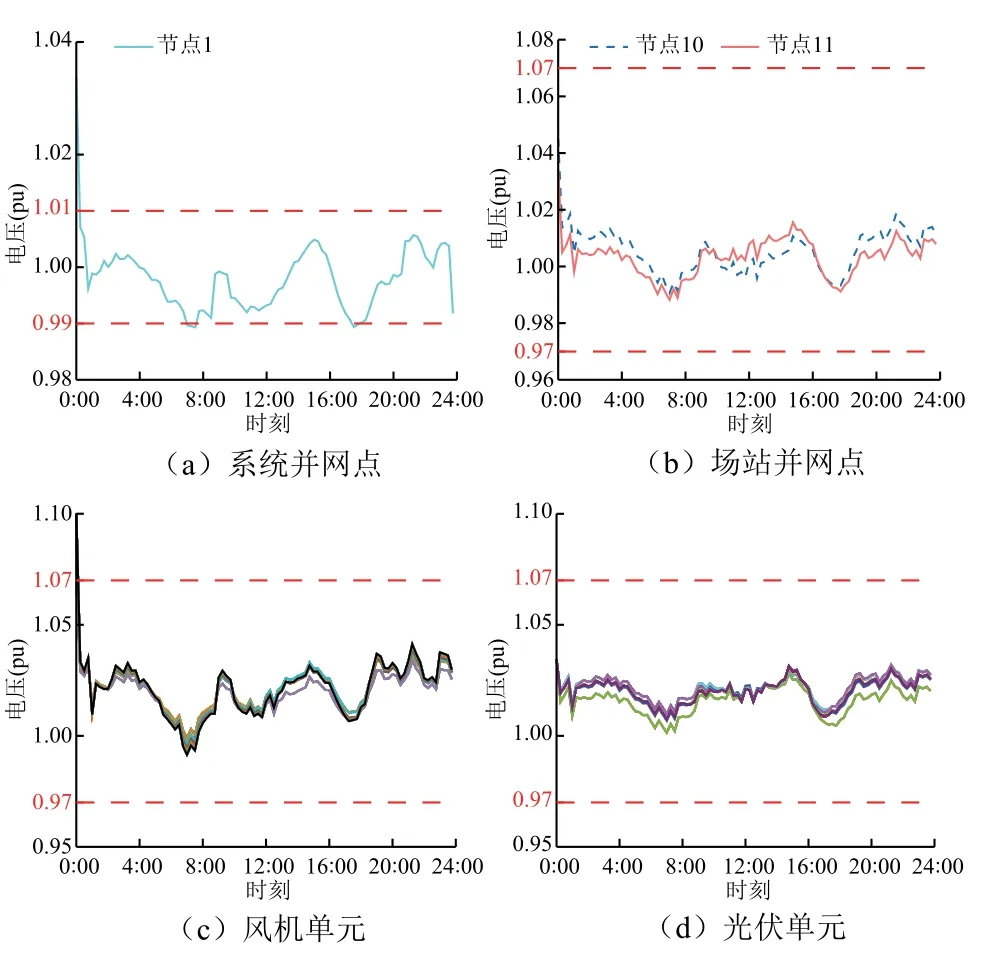
圖15 穩壓控制下大連耦合系統各并網點電壓運行結果Fig15 Voltage flucatuation of PCC in the Dalian coupled system with voltage stability control

圖16 不同控制方式下大連耦合系統網損情況Fig16 Network loss of Dalian coupling system with different control modes

5 結論

本文針對由新能源場站與同步機組構成并經外送通道功率送出的耦合系統，結合其單元-場站-系統的物理層級特征，建立了系統層-場站層的分層協同電壓優化控制架構，兼顧運行網損優化和電壓安全控制需求，構建了綜合MPC 和ADMM 的電壓校正與網損優化模式自適應切換的分層協同優化控制策略。針對耦合系統仿真，得到以下結論：

1）本文所提出的分層控制框架中，系統層與場站層之間只需交互公共邊界節點電壓信息，各場站之間無需通信，可有效滿足不同主體運營商之間的信息隱私保護要求，在應對具有信息壁壘的耦合系統電壓控制問題上有較大優勢。

2）本文所提出的滾動時域控制策略在應對新能源隨機波動導致的電壓強波動問題上，電壓控制魯棒性好，所采用的分布式協同方法將復雜的全局電壓優化控制問題分解為多個子優化控制問題，降低了模型規模和求解難度。

3）本文所提出的控制策略能夠可靠滿足耦合系統中各類型并網點電壓的安全控制需求，并有效減少耦合系統的運行網損，同時提升了耦合系統電壓安全性和運行經濟性。

附 錄

1.修改的IEEE-14 節點耦合系統相關設置

附圖1 修改的IEEE-14 節點耦合系統中系統層無功源控制狀態App.Fig.1 Variation of var control variables in the system layer of the modified IEEE-14 coupled system

附圖2 修改的IEEE-14 節點耦合系統中場站層控制狀態App.Fig.2 Variation of var control variables in the layer of new energy station of the modified IEEE-14 coupled system

附圖3 修改的IEEE-14 節點耦合系統中殘差收斂曲線App.Fig.3 Convergence curves of residual of the modified IEEE-14 coupled system

2.大連某區域電網相關設置

附圖4 大連耦合系統中系統層無功源控制狀態App.Fig.4 Variation of var control variables in the system layer of Dalian coupled system

圖5 大連耦合系統中場站層控制狀態App.Fig.5 Variation of var control variables in the layer of new energy station of Dalian coupled system

附圖6 大連耦合系統中殘差收斂曲線App.Fig.6 Convergence curves of residual of Dalian coupled system