考慮參數誤差的無速度傳感器異步電機低速發電工況穩定性提升策略

楊 凱 李孺涵 羅 成 徐智杰 鄭逸飛

（華中科技大學電氣與電子工程學院 武漢 430074）

0 引言

異步電機無速度傳感器控制系統以其結構簡單、體積小、成本低、易于維護等優點，被廣泛應用于工業生產中[1]。近年來，使用自適應全階觀測器獲取轉速與位置信息的轉速辨識方案成為主流[2]。然而，異步電機無速度傳感器系統在低速發電區域穩定性較差，且對電機參數變化十分敏感[3]。

為了提高異步電機無速度傳感器控制系統的穩定性與轉速觀測性能，現有文獻做了大量的探索：

1）基于全階觀測器的信號注入法。為實現低速發電區域特別是定子電流近零頻時的穩定轉速觀測，可在觀測器中注入虛擬電壓信號[4]。然而，虛擬電壓注入會造成轉速觀測誤差和轉矩脈動。

2）修正轉速自適應律。文獻[5]通過引入電流誤差的d 軸分量修正轉速自適應律，并使用勞斯判據獲得引入分量的取值范圍，在一定程度上增強了全階觀測器的穩定性。

3）設計誤差反饋矩陣。此類方法利用觀測器誤差反饋矩陣設計，減少甚至消除低速發電工況下不穩定運行區域[6]。為提高全階觀測器的參數魯棒性，文獻[7]對不同的反饋矩陣設計方法進行了對比和改進。然而，反饋矩陣中的四個待定參數難以統籌設計。

上述方法可在一定程度上提高基于自適應全階狀態觀測器（Adaptive Full-order Observer, AFO）的無速度傳感器異步電機控制系統在低速發電區域運行的穩定性。現有方法均采用穩定性理論[8]或極點配置方法[9]設計反饋矩陣。如果在全階觀測器中使用的電機參數完全準確，理論上可以將不穩定區域削減至定子電流零頻線。然而，由于電機參數存在誤差，現有方法無法完全消除不穩定區域。因此，異步電機無速度傳感器控制系統在低定子電流頻率區域仍然會失穩。

提高現有方法對參數誤差的魯棒性，提升全階觀測器在低速發電區域的穩定性，已成為亟待解決的問題。現有研究方法因無法獲得實際的轉子磁鏈信息，大多無法采用磁鏈誤差。因此，通過已知信息構建磁鏈誤差項，并協同電流誤差與磁鏈誤差改進反饋矩陣設計，具有一定的研究價值。

已有研究表明，異步電機與其全階觀測器之間的電流誤差項由不同分量組成，且誤差分量是電機參數的函數[10]。類似地，磁鏈誤差項也可以視為不同分量的疊加[11]。基于此，文獻[12]假設定子電阻和轉子轉速存在觀測誤差，通過構建磁鏈誤差表達式重新設計了反饋矩陣和轉速自適應律。然而，異步電機無速度傳感器矢量控制系統對轉子電阻參數攝動也較為敏感[13]，在線觀測磁鏈誤差時必須考慮轉子電阻誤差的影響。

為解決上述問題，本文充分利用電機狀態信息，提出了一種基于多誤差項協同的反饋矩陣設計方法，以提高觀測器的參數魯棒性，保證系統在低速發電區域的穩定性。本文假設轉速、定子電阻、轉子電阻均存在觀測誤差，使用多誤差項解耦方法，推導出磁鏈誤差表達式。在此基礎上，協同電流誤差項與磁鏈誤差項，設計新型反饋矩陣，以滿足系統穩定的必要條件。與文獻[12]不同，本文所提出的磁鏈誤差觀測表達式是同步轉速和轉差轉速的函數，對電機的實際運行工況具有良好的跟蹤效果。

本文首先給出異步電機及自適應全階觀測器的數學模型，揭示傳統反饋矩陣設計存在的缺陷，提出一種基于多誤差項解耦的磁鏈誤差觀測方法；然后，協同電流誤差項與磁鏈誤差項，設計反饋矩陣；最后，使用2.2 kW 異步電機實驗平臺進行負載階躍、轉速切換、帶載轉速階躍、定轉子電阻失配等實驗。

1 異步電機與全階觀測器模型

1.1 異步電機模型

選取定子電流與轉子磁鏈作為狀態變量，則兩相靜止坐標系下異步電機的數學模型為

其中

式中，is、ψr、su分別為定子電流矢量、轉子磁鏈矢量、定子電壓矢量；ωr為轉子電氣角速度；Tr為轉子時間常數；Ls、Lr、Lm分別為異步電機定子電感、轉子電感、以及定、轉子繞組之間的互感；Rs和Rr分別為定子電阻和轉子電阻。

1.2 全階觀測器模型

異步電機無速度傳感器矢量控制系統的全階觀測器模型可以由式（1）導出為

將式（1）減去式（2），可得誤差矢量表達式為

其中

基于式（3），使用波波夫超穩定性定理即可得到轉子轉速的自適應律[14]為

式中，Kp和Ki為轉速觀測器的自適應增益。

1.3 傳統反饋矩陣的不穩定問題

為了分析異步電機無速度傳感器矢量控制系統的穩定性，基于轉速自適應律式（4），將誤差矢量式（3）擴展為

進而，在兩相同步旋轉坐標系下，針對某一確定的工作點，擴展的誤差矢量可以線性化地表示為

式中，A1為線性化誤差矢量系數矩陣，具體表達式詳見附錄式（A1）。

基于式（6），低速發電工況下的不穩定區域邊界計算式[15]為

求解式（7），可得兩個有關同步轉速和轉子轉速的等式見式（8），式（8）也為有反饋矩陣時不穩定區域的邊界。

式中，l=σLsLrTrh1+RsLrTr；eω為同步轉速。

若式（8）中采用零反饋矩陣，可得傳統低速發電不穩定區域的邊界為

若將文獻[16]中的反饋矩陣代入式（8），理論上可以使邊界線L2和L1重合，消除式（9）中低速發電工況下的不穩定區域。然而，實際應用場景下電機控制系統中使用的參數（定子電阻、轉子電阻等）與電機實際的參數無法實現完全匹配。以文獻[16]中提出的反饋矩陣為例，分析傳統方法對電機參數的敏感性。若定子電阻存在誤差，邊界線L2變為

根據式（10）可知，即使采用反饋矩陣，由于定子電阻誤差，邊界線L2依然無法完全與L1重合。基于式（10），圖1 給出了采用反饋矩陣時邊界線L2隨不同轉速和定子電阻誤差的變化示意圖。從圖1可以看出，邊界線L2明顯偏離零平面。說明在低速發電工況下，電機參數存在誤差時，不穩定區域仍然存在，導致控制系統在實際應用中失去穩定性。上述分析表明，由于電機參數誤差，傳統反饋矩陣設計策略無法完全消除不穩定區域，對參數誤差敏感，難以滿足系統穩定的必要條件。

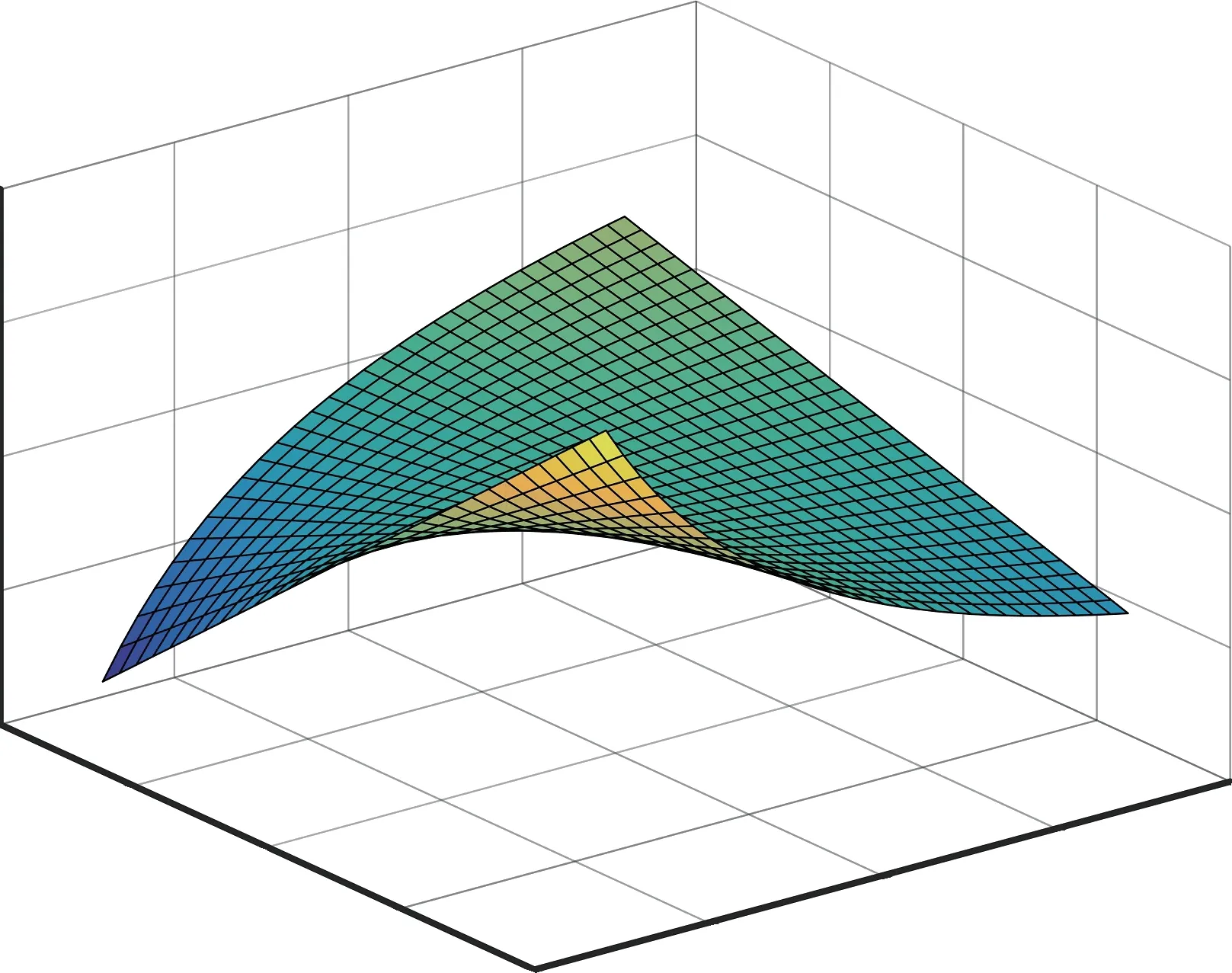
圖1 有反饋矩陣時，邊界線L2 值隨不同轉子轉速和定子電阻誤差變化示意圖Fig.1 Variations of line L2 against stator resistance uncertainties and rotor speed with the feedback matrix

2 磁鏈誤差解耦觀測

傳統轉速觀測方法在電機參數存在誤差時，難以滿足系統穩定的必要條件。由于轉子磁鏈未知，現有方法無法在觀測器中使用磁鏈誤差設計誤差反饋矩陣。為了在第3 節中引入磁鏈誤差并設計多誤差項協同的反饋矩陣，本節提出一種基于多誤差項解耦的在線磁鏈誤差觀測方法。

2.1 磁鏈誤差分析

假定反饋矩陣為0 對式（3）進行拉普拉斯變換，可以得到

消除式（11）中的磁鏈誤差，可以得到無反饋矩陣下的定子電流誤差表達式為

其中

少先隊員是一種兒童的群眾性組織，十九大的勝利召開，對培養少先隊員提出了新的要求和目標。在培養少先隊員的過程中，要進行組織教育和實踐活動相結合的方式。引導廣大少先隊員聽黨的話，跟著黨走，讓他們從小學習怎樣做人，樹立正確的世界觀和價值觀，形成良好的行為習慣和學習習慣，有自己的目標，從小立志，做一個正直的人，不斷努力提高自身思想道德修養和文化水平，為實現中華民族的偉大復興而奮斗。

且有

由式（12）與式（13）可知，定子電流誤差可以視為三項誤差之和：轉子轉速誤差項、定子電阻誤差項、轉子電阻誤差項。類似地，消除式（11）中的電流誤差，也可得到無反饋矩陣下的轉子磁鏈誤差表達式為

其中

由式（14）與式（15）可知，轉子磁鏈誤差也可視為轉子轉速誤差項、定子電阻誤差項、轉子電阻誤差項之和。則在兩相同步旋轉坐標系下，定子電流誤差與轉子磁鏈誤差的關系可以依下列步驟得到。

1）假設只存在轉子轉速誤差，不存在定子電阻和轉子電阻誤差。基于式（12）～式（15），可得定子電流誤差和轉子磁鏈誤差的比值為

為了表示誤差矢量關系，其矢量比值關系由推導過程中矩陣記號變為復平面矢量記號。

2）假設只存在定子電阻誤差，不存在轉子轉速和轉子電阻誤差。基于式（12）～式（15），可得定子電流誤差和轉子磁鏈誤差的比值為

式中，sω為轉差轉速。

4）在電機實際運行過程中，轉速誤差、定子電阻誤差、轉子電阻誤差同時存在。為進一步探究磁鏈誤差表達式中不同誤差項之間的關系，進而確定合理的磁鏈誤差表達式，綜合上述三種情況，引入加權復系數k1、k2、k3，可得磁鏈誤差項表達式為

其中

將式（16）～式（18）代入式（19），可得

選擇合適的權重系數k1、k2、k3，即可利用式（20）完成對轉子磁鏈誤差的在線觀測。式（20）說明本文提出的轉子磁鏈誤差觀測表達式是同步轉速ωe和轉差轉速ωs的函數，即所提出的方法可以實現對異步電機運行工況的跟蹤。

2.2 權重取值討論

轉子磁鏈誤差表達式（20）中有三個待定的權重系數。為簡化分析，設

在兩相同步旋轉坐標系中，根據式（21）的計算，穩態下系數N1、N3的表達式分別為

式中，ξ=Δωr/ΔRs；i?sd、i?sq分別為d 軸、q 軸電流觀測值。

基于式（22），可繪出系數N1和N3在不同轉矩電流和同步轉速下的變化情況，分別如圖2 和圖3所示。圖中，轉矩電流從0 變化至6.1A，同步轉速從0 變化至150 r/min（31.4 rad/s）。根據圖2 和圖3，系數N1和N3的值與同步轉速以及轉差轉速有關。當同步轉速變小時，系數N1和N3的值變化幅度變小。當同步轉速為零時，系數N1和N3的值也隨之變為零。

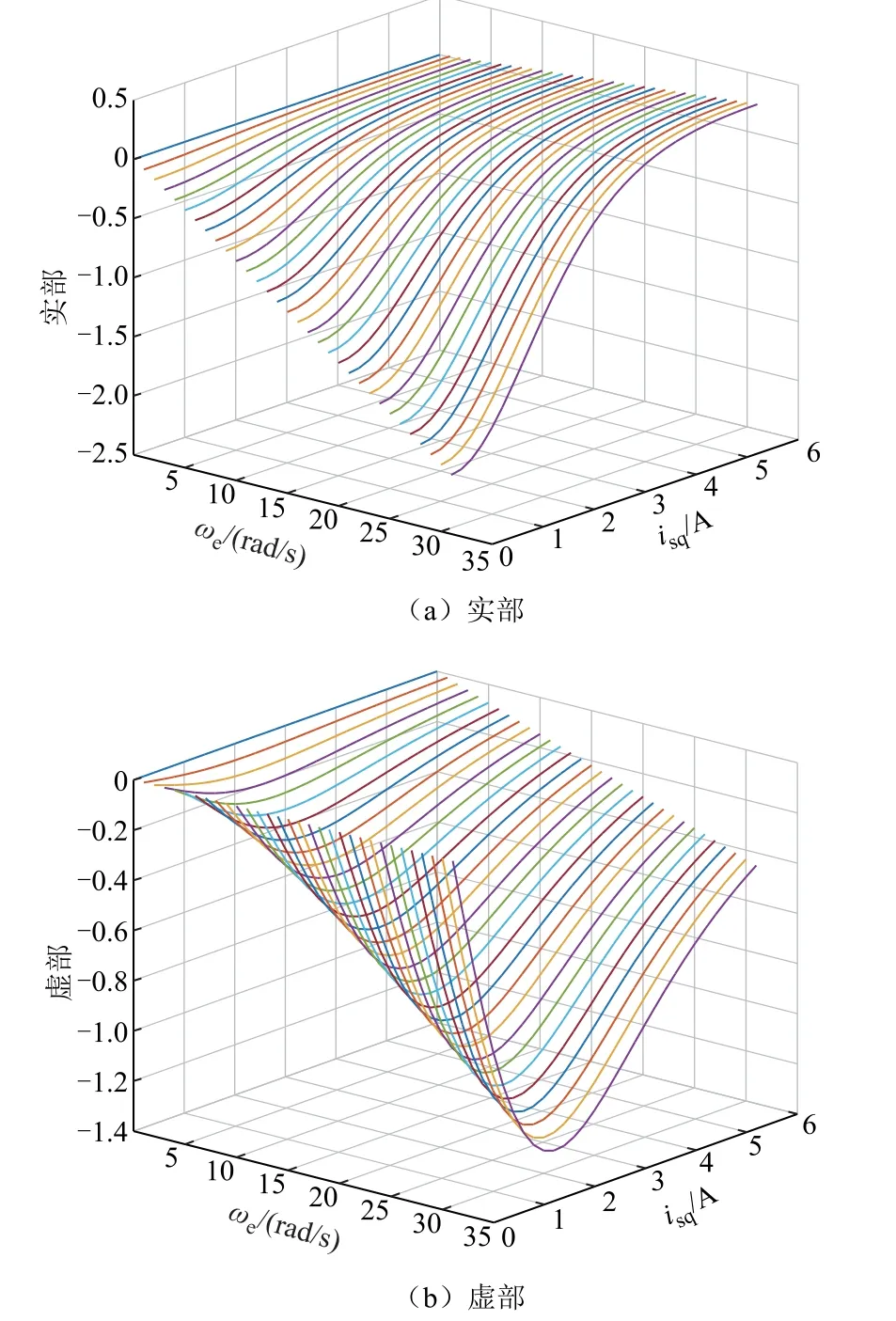
圖2 系數N1 在不同轉矩電流和同步轉速下的變化Fig.2 Ratio N1 against different synchronous speeds and torque currents

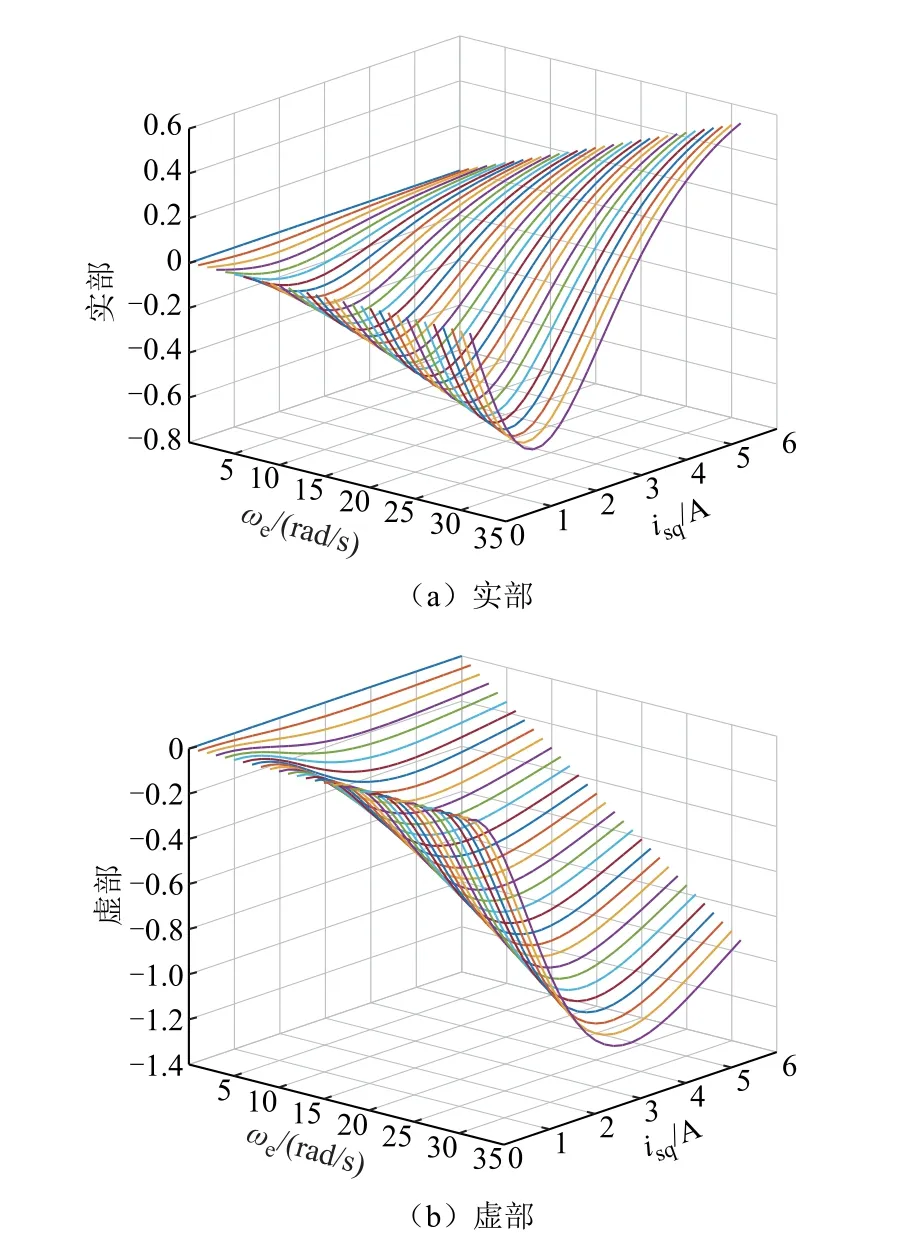
圖3 系數N3 在不同轉矩電流和同步轉速下的變化Fig.3 Ratio N3 against different synchronous speeds and torque currents

采用系數N1和N3，式（20）變為

也可寫為

對比式（24）與式（19）可知，權重k1、k2、k3與系數N1和N3之間的關系為

根據式（25），選擇權重系數k1、k2、k3的取值，進而使用式（20）即可完成磁鏈誤差在線觀測。然而，式（20）中過低的同步轉速會導致觀測磁鏈誤差項虛部過大，造成處理器數據溢出。因此，在實際的操作系統中需要對同步轉速進行限制。

3 基于多誤差項協同的反饋矩陣設計

將觀測磁鏈誤差項引入全階觀測器，本節提出一種基于多誤差項協同的反饋矩陣設計方法。

3.1 多誤差項協同設計

較之于式（2）中的傳統全階觀測器模型，多誤差項協同設計的全階觀測器同時將定子電流誤差和轉子磁鏈誤差納入設計，其狀態方程可表示為

式中，G為反饋矩陣，

采用本文所提出的方法，無速度傳感器感應電機系統控制框圖如圖4 所示。電流內環和轉速外環構成異步電機雙閉環矢量控制系統，全階觀測器協同電流誤差項與磁鏈誤差項，輸出估計轉速與轉子位置角信息，實現對異步電機的無速度傳感器控制。

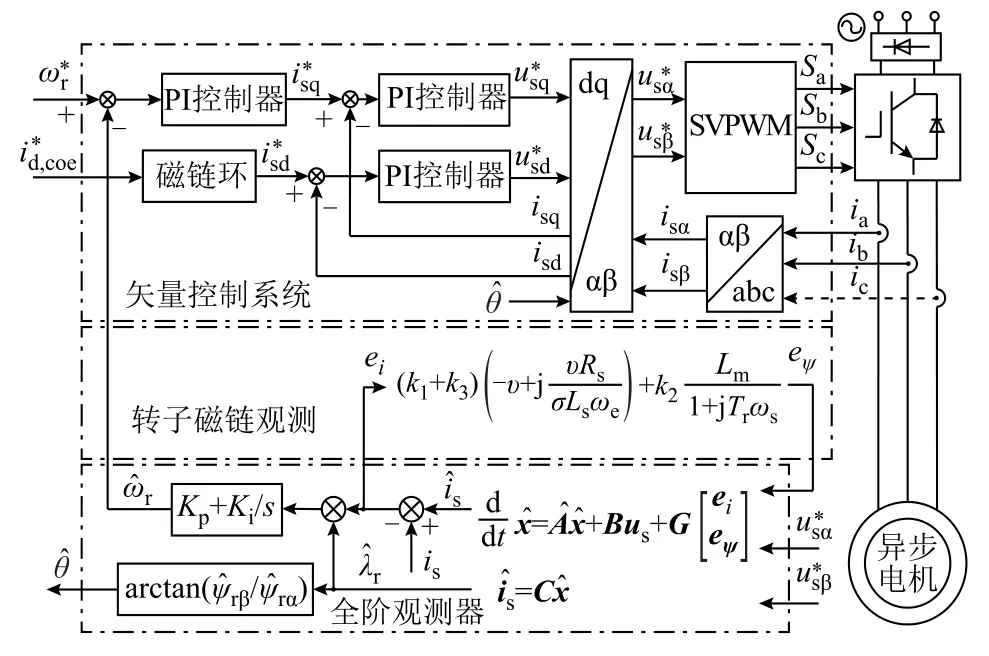
圖4 基于改進反饋矩陣設計的系統控制框圖Fig.4 Block diagram of the control system with the proposed feedback matrix design

3.2 穩定函數最值與魯棒性提升設計

基于式（26），帶有磁鏈誤差項的全階觀測器的擴展誤差矢量表達式可線性化為

式中，A5為帶有磁鏈誤差項的全階觀測器的線性化誤差矢量系數矩陣，表達式見附錄式（A2）。

要保持控制系統穩定，誤差系數矩陣A5的所有特征根均須具有負實部。對于五階誤差系數矩陣A5，其行列式的值需為負。由此可得全階觀測器式（26）穩定的必要條件為

式中，函數f(ωe,ωr)具體表達式詳見附錄式（A3）。

特別地，當函數f(ωe,ωr)取值為0，即為異步電電機無速度傳感器矢量控制系統在低速發電區域的不穩定邊界線。

針對不同反饋矩陣設計方法，利用函數f(ωe,ωr)將不穩定區域的變化繪制于圖5 中。據圖5 可知，函數f(ωe,ωr)是一條關于同步轉速ωe的拋物線。當參數誤差存在時，現有方法并不能使不穩定邊界線L2和L1重合，無法滿足式（28）。為解決這一問題，改進設計方法通過引入常數項將函數f(ωe,ωr)沿y軸負方向移動，使其最大值（拋物線頂點）為負。進而，保證不穩定邊界線L2和L1重合。此外，改進設計也可以保證式（28）所示的穩定條件被滿足，保證反饋矩陣的設計對參數誤差有良好的魯棒性。

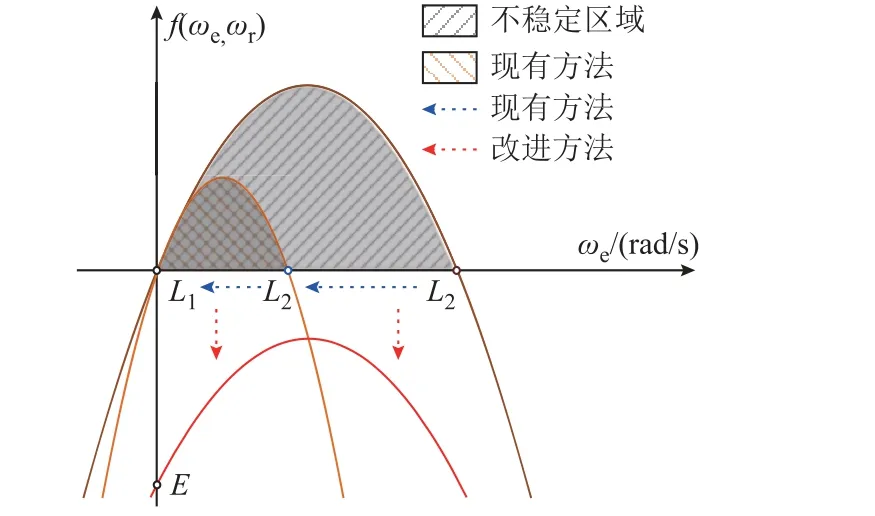
圖5 不同方法下的不穩定區域變化示意圖Fig.5 The unstable regenerating region under traditional method and proposed method, respectively

結合上述分析，為滿足穩定的必要條件，函數f(ωe,ωr)需滿足其頂點處的函數值小于零，即

式中，m1＜0，m1～m3的表達式見附錄。

為簡化反饋矩陣設計過程，假設

將式（30）代入式（29）中，可得

滿足式（31）的參數g3可設計為

綜上所述，改進的反饋矩陣可以設計為

式中，?0＞，并且。

采用式（33）所示的反饋矩陣可在穩定性必要條件的二次函數中引入常數項，將拋物線向y軸負方向移動。通過調整常數項，可滿足系統穩定的必要條件，提高觀測器對電機參數誤差的魯棒性。

4 實驗驗證

4.1 實驗平臺介紹

為驗證所提出方法的有效性，基于STM32F103 ARM 的2.2 kW 異步電機實驗平臺進行實驗，如圖6 所示，該平臺使用兩臺同軸連接的三相籠型異步電機，分別用于測試本文所提出方法以及提供實驗所需負載。實驗平臺所用電機額定參數見表1。實驗用異步電機工作在6 kHz PWM 開關頻率下的矢量控制模式。電機勵磁電流設置為額定值的50%，轉速自適應律Kp設置為2.0，Ki設置為500。

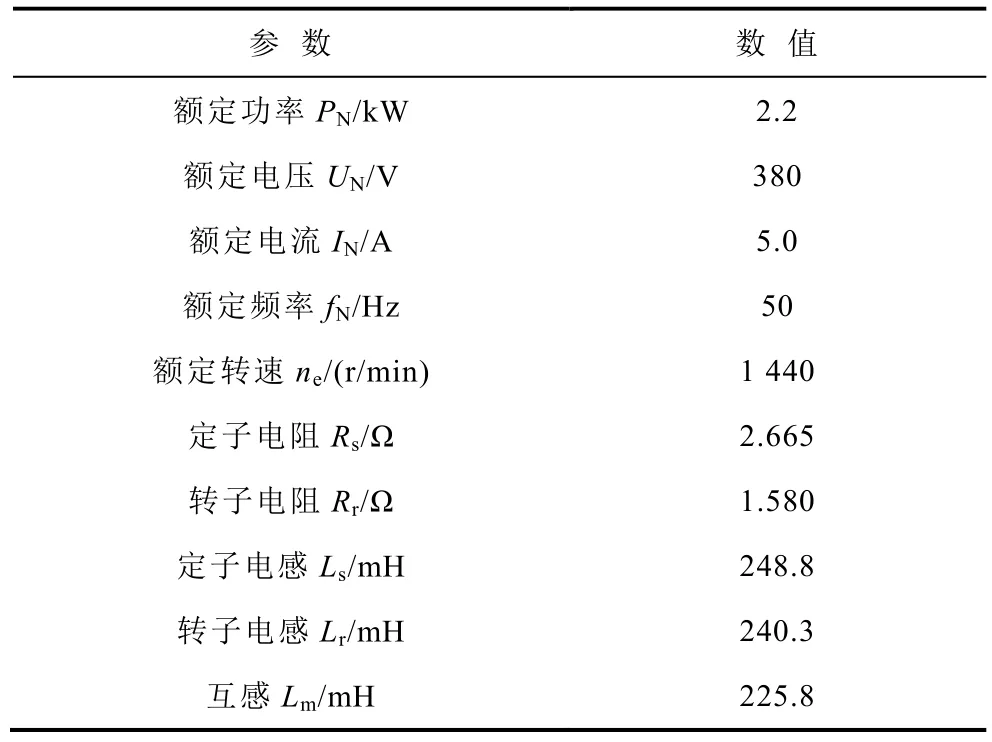
表1 2.2 kW 異步電機參數Tab.1 2.2 kW IM parameters

圖6 2.2 kW 異步電機實驗平臺Fig.6 IM experimental setup

4.2 負載階躍實驗

驗證異步電機無速度傳感器控制系統性能的一個重要方法是在低速發電工況下進行負載階躍實驗。負載階躍對比實驗結果如圖7 所示。

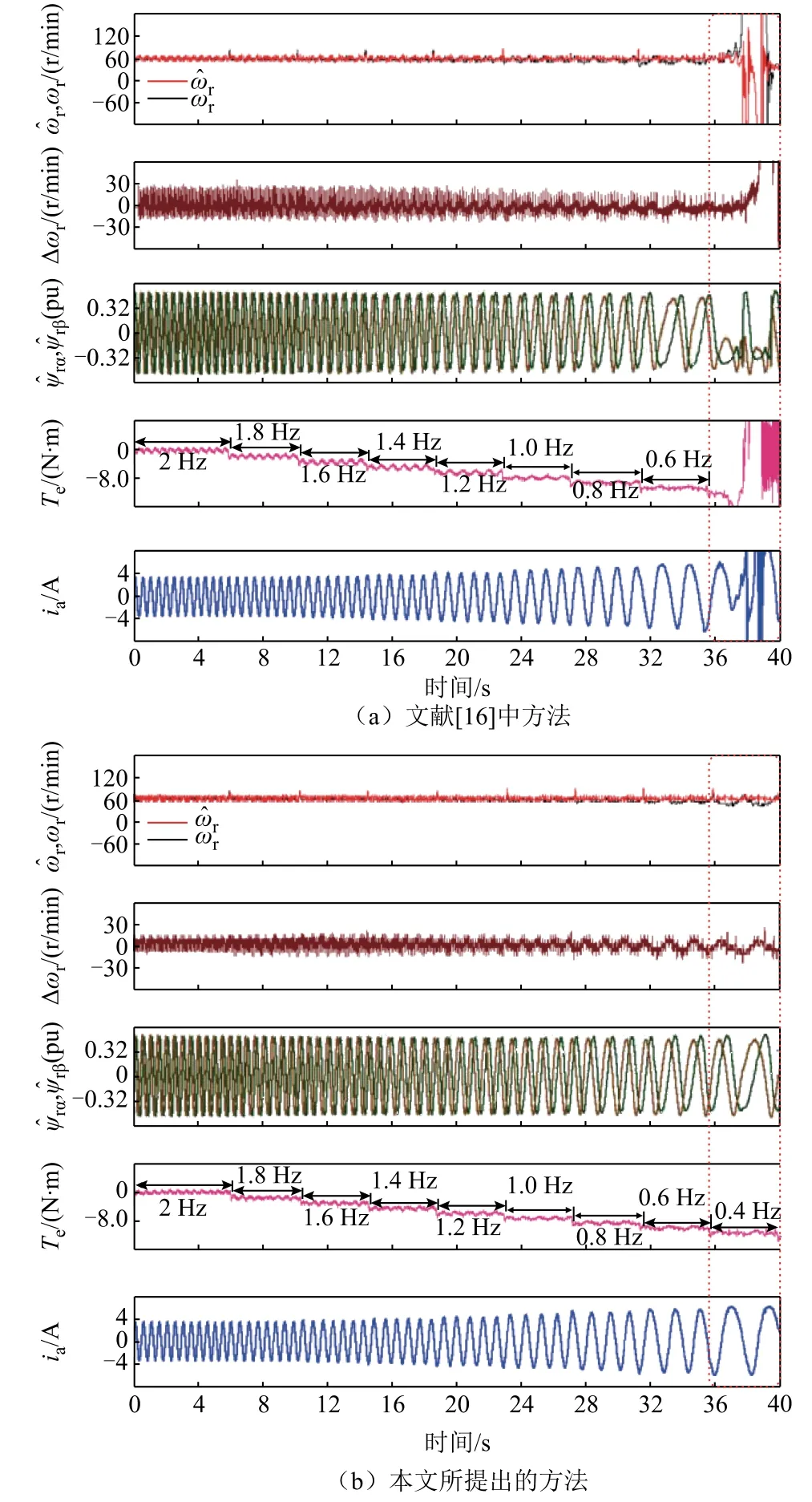
圖7 低速發電工況下負載階躍實驗Fig.7 Performance during step load change in low speed

在圖7a 中，轉子轉速設置為60 r/min，負載從0 開始階躍變化，每4 s 階躍變化-10%額定值，其全階觀測器使用文獻[16]中的反饋矩陣。將異步電機同步轉速標注于圖中，可知傳統方法下，同步轉速小于0.6 Hz 時異步電機無速度傳感器矢量控制系統將失穩。圖8a 所示為圖7a 中ωr-Te坐標系下電機運行工況點軌跡圖。圖8a 中，運行工況點軌跡發散，電機控制系統失穩。

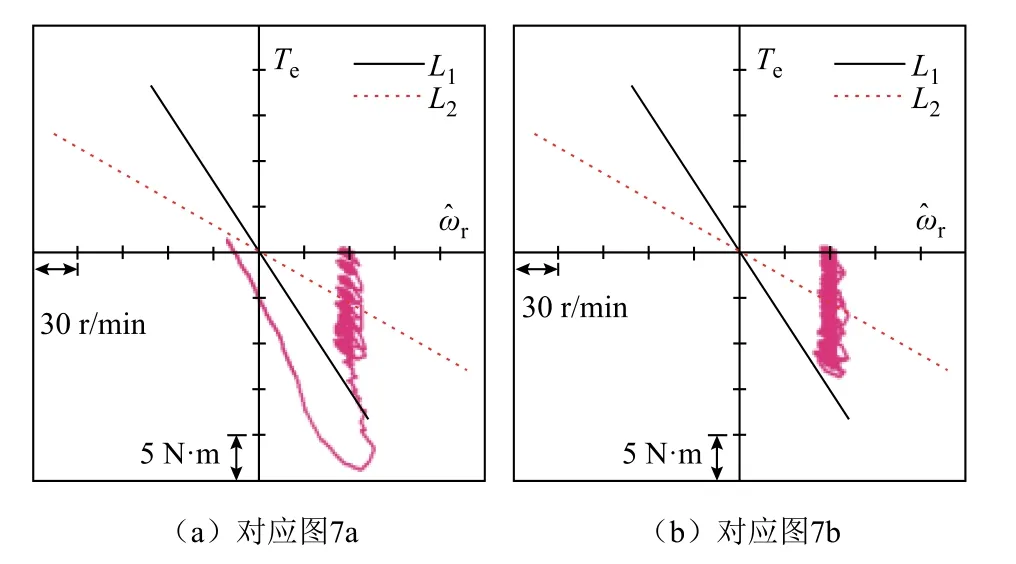
圖8 ωr-Te 坐標系下電機運行工況點軌跡Fig.8 The IM operating point trajetory in ωr-Te graphs

對比實驗使用本文提出的改進反饋矩陣，實驗結果如圖8b 所示。將異步電機同步轉速標注于圖中，可知本文所提出的方法下，同步轉速為0.4 Hz時系統仍然處于穩定狀態。在圖8b 中，可以觀察到異步電機運行工況點已十分接近定子電流零頻線L1，系統仍然保持穩定運行。同時，對比兩者的轉速估計誤差可以發現，所提出的反饋矩陣的低速穩定性方法能夠有效地抑制轉速脈動。對比實驗驗證了所提出方法在長時間低頻穩態工況下對系統穩定性提升的有效性。

4.3 轉速切換實驗

為驗證本文提出的方法在低速發電區域的有效性，設置150 r/min 和-150 r/min 之間的轉速切換實驗，結果如圖9 所示。

為提供更寬的觀察范圍，使電機運行工況點完整穿過低速發電不穩定區域并折返，檢驗所提出方法在不同低速區間的表現，設置±150 r/min 的轉速切換指令。在±150 r/min 之間的切換時間設置為11 s，負載轉矩設置為8 N·m。據圖9 可知，所提出的方法在穩態和動態下均能保持轉速穩定可觀測。與圖9a 對應的ωr-Te坐標系下電機運行工況點軌跡如圖9b 所示。運行工況點軌跡在不穩定邊界線L1附近時系統仍然保持穩定，并可以成功穿越傳統不穩定區域，驗證了所提出方法的有效性。

4.4 帶載轉速階躍變化實驗

為檢驗本文所提出方法在帶載轉速階躍變化工況下系統的動態和穩態轉速跟蹤性能，進行帶載轉速階躍變化實驗，如圖10 所示。帶載工況下，轉速從0 階躍變化至120 r/min，每步階躍時間為0.12 s，每步轉速階躍變化60 r/min。實驗中，估計轉速快速跟蹤實際轉速，異步電機無速度傳感器矢量控制系統在實驗中始終保持穩定。此外，在零速帶載階段，本文所提出的方法也能夠保持系統的穩定性。

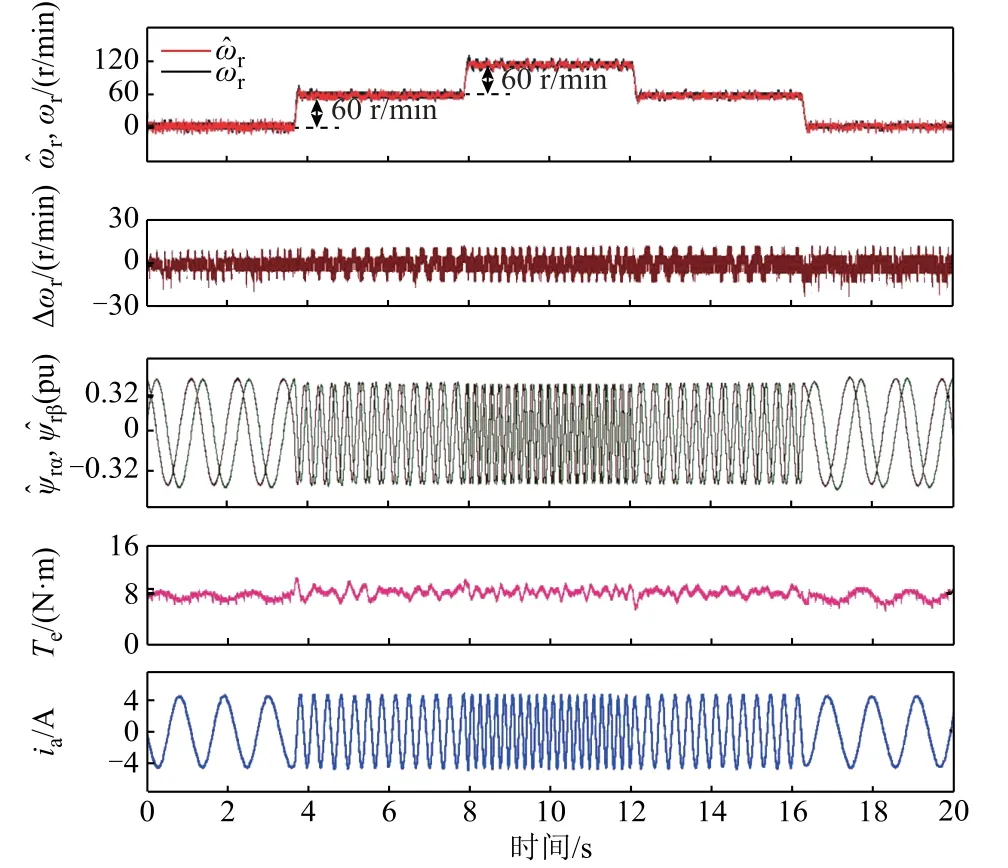
圖10 帶載轉速階躍變化實驗Fig.10 Experiments during sudden speed changes under loaded condition

4.5 電阻失配實驗

無速度傳感器異步電機控制系統在低速時對電阻參數變化，尤其是定子電阻變化較為敏感，當電阻參數存在誤差，轉速觀測可能會失敗[17]。為驗證本文提出的方法對電阻誤差的魯棒性，分別在±30%定子電阻和±30%轉子電阻誤差下進行實驗，結果如圖11 和圖12 所示。為最小化全階觀測器本身對電機參數的敏感性，系列實驗在空載條件下進行。

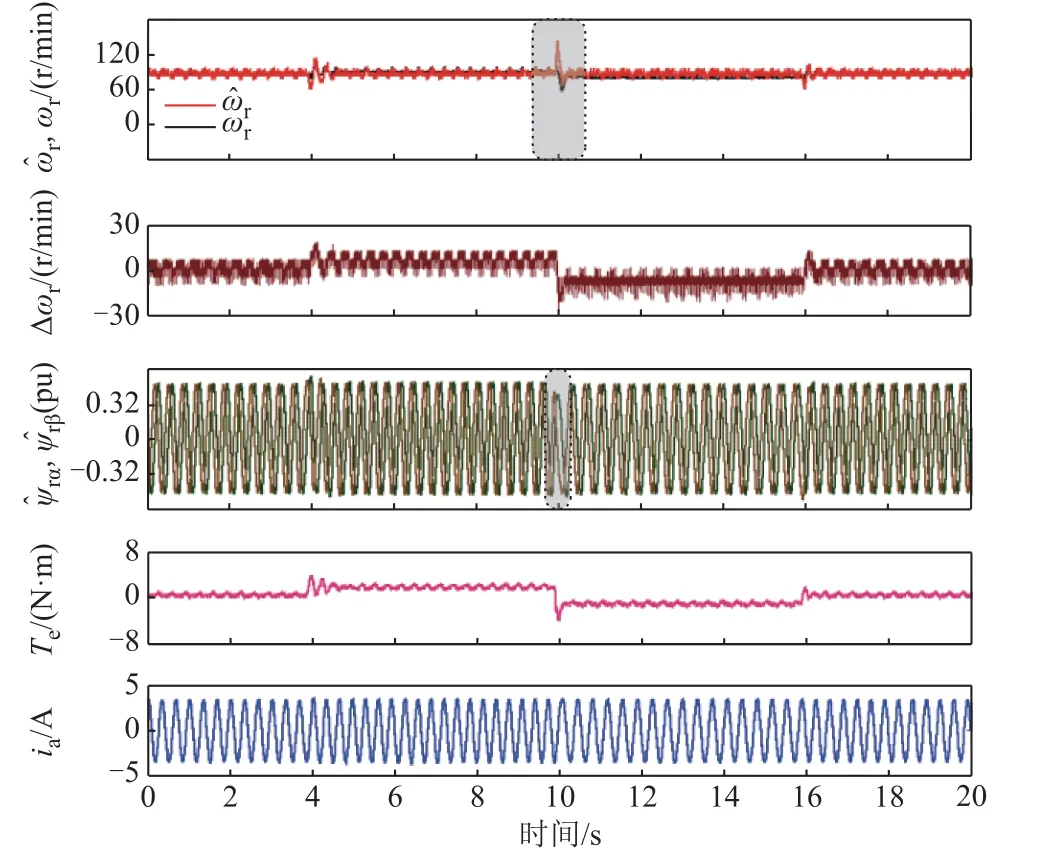
圖11 ±30%定子電阻誤差實驗Fig.11 Results with ±30% stator resistance mismatches

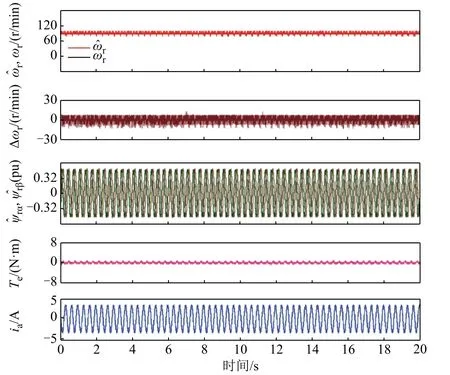
圖12 ±30%轉子電阻誤差實驗Fig.12 Results with ±30% rotor resistance mismatches

在圖11 中，轉子轉速為90 r/min，分別在4～10 s 和10～16 s 注入+30%和-30%定子電阻誤差，檢驗所提出方法對定子電阻誤差的魯棒性。由圖11可知，定子電阻突變將造成估計轉速瞬時波動，而后估計轉速收斂。注入的定子電阻誤差將導致估計轉速與實際轉速之間的穩態誤差，但無速度傳感器系統始終保持穩定，說明本文所提方法對電機定子電阻誤差具有良好的魯棒性。圖12 中實驗轉速、負載設置、誤差注入時序與圖11 保持一致。由圖12可知，轉子電阻誤差幾乎沒有對系統的控制性能造成影響。電機相電流和轉子磁鏈均保持良好正弦波形，轉速觀測始終保持穩定。實驗結果充分說明本文提出的方法對轉子電阻參數誤差有良好的魯棒性。

綜上所述，本文通過負載階躍實驗、轉速切換實驗、帶載轉速階躍實驗、定/轉子電阻失配實驗等系列實驗，從不同角度驗證了本文所提出的基于多誤差項協同的反饋矩陣設計方法在低速發電區域運行時的穩定性、對轉速指令的跟蹤性能、對電機參數誤差的魯棒性。本文實驗的定性對比見表2。

表2 本文實驗定性分析Tab.2 The qualitative analysis of experiments

5 結論

本文提出了一種無速度傳感器異步電機低速發電工況穩定性提升方法，提高了系統在低速發電區域運行時對電機參數誤差的魯棒性。通過推導磁鏈誤差表達式，基于多誤差項解耦，分析權重參數，將磁鏈誤差項引入全階觀測器進行狀態反饋，協同電流誤差與磁鏈誤差設計反饋矩陣。基于所提出的反饋矩陣設計，即使存在電機參數誤差，也可以滿足系統穩定的必要條件，提高自適應全階觀測器對電機參數誤差的魯棒性。使用2.2 kW異步電機實驗平臺驗證了所提出方法的有效性。即使定、轉子電阻存在30%誤差，系統仍然可以保持穩定運行。

附 錄

1.誤差系數矩陣A1、A5

對式（5）進行小信號線性化，可得傳統反饋矩陣下系統的五階誤差系數矩陣A1為

其中

同理，式（27）中，基于本文提出的反饋矩陣設計方法，系統的五階誤差系數矩陣A5為

其中

2.函數f(ωe,ωr)表達式

式（28）所示函數f(ωe,ωr)的具體表達式可以通過計算五階誤差系數矩陣A5的行列式得到，為

其中