一種考慮動態磁滯效應的高效穩定時域有限元計算方法

魏 鵬 陳 龍 賁 彤 井立兵 張 獻

（1.三峽大學電氣與新能源學院 宜昌 443002 2.湖北省微電網工程技術研究中心（三峽大學） 宜昌 443002 3.省部共建電工裝備可靠性與智能化國家重點實驗室（河北工業大學） 天津 300130）

0 引言

時域有限元方法廣泛應用于電工裝備的運行狀態預測與損耗評估之中[1]，準確預測電機、變壓器等電工裝備的時域暫態損耗分布特性不僅對降低設備能耗、改善局部過熱具有重要意義，同時考慮損耗對暫態磁場求解的反饋作用，對進一步分析電工裝備的瞬時功率平衡、暫態勵磁特征等電磁特性至關重要[2-4]。

目前，對于電工裝備鐵心損耗的有限元計算方法可大致分為兩類：一是基于場計算結果的后處理方法，該類方法利用Steinmetz 損耗模型或Bertotti統計學損耗分離理論對僅單值非線性磁場的計算結果進行后處理，得到每一個單元的損耗，最終進行積分得到電工裝備整體的損耗[5-7]。這一類方法主要用于對電機或變壓器的損耗進行頻域分析，并通過傅里葉變換來分析含有諧波激勵時的鐵心損耗。Ansys 公司D.Lin 等基于等效橢圓環思想，將上述方法進行了時域瞬時功率損耗計算擴展[8]。該方法的優勢在于在損耗計算過程中無需迭代，在磁路簡單的結構中具有較好的精度，但由于沒有考慮鐵心磁滯、渦流損耗、剩余損耗等效動態磁場對鐵心中磁場分布的反饋作用，在電機等復雜磁路電工裝備的損耗計算中將帶來較大誤差。另一類鐵心損耗計算方法則是在時域有限元分析中，考慮動態磁滯效應對每一瞬時的功率損耗進行精確求解[9-10]。這一類方法可最大限度地模擬鐵心的真實磁化過程，在處理含有磁通密度波形畸變工況下的損耗計算問題時具有較高精度。同時，在考慮鐵心動態磁滯效應后，鐵心中動態磁滯回線波形的精確模擬可在時域中對勵磁電流的波形進行實時反饋，進而可對電機或變壓器中暫態運行特性進行有效預測。因此，電工裝備損耗的精確預測與運行狀態的有效評估都離不開在時域有限元分析時對動態磁滯特性的影響的考慮。

然而，目前在有限元分析中常用的磁滯模型，如J-A 模型[11-13]、Preisach 模型[14-17]等均是與磁化速率無關的磁滯模型，并不能直接考慮電機或變壓器疊片宏觀渦流損耗與剩余損耗等動態因素對鐵心磁場分布的影響。為此，需要進一步將二者的等效動態磁場考慮到有限元的計算方程之中。傳統方法是將動態效果等效為電導率乘以磁矢位A對時間的一階導數，但該種等效僅適合均勻實心區域渦流路徑的求解，并不適合疊片鐵心結構[18-19]。對于鐵心疊片結構，進行實際三維建模將會帶來無法承受的計算成本。為此，E.Dlala 等提出了一種耦合一維疊片有限元方法的二維時域有限元計算方法[20-21]。在疊片維度，忽略邊緣效應，認為磁通密度僅是疊片厚度方向上的函數，進而僅需要求解一維有限元方程，即可得到疊片的渦流損耗等效磁場。然而，該方法實質上是在二維有限元計算中嵌套了一維有限元程序，仍具有較高的求解難度。為了對上述求解方法進行簡化，目前常采用Bertotti 模型的變形形式，即在耦合靜態磁滯模型的過程中，通過耦合等效微分磁阻率來考慮渦流損耗磁場與剩余損耗磁場的效果，該方法避免了一維有限元的求解，在一定程度上大大簡化了計算，但在每次迭代過程中仍需更新磁阻率和剛度矩陣，導致計算效率低下[22-23]。因此，在進一步求解含有等效磁阻率的方程時，需要進一步耦合非線性磁場計算中的固定點迭代技術。在僅考慮靜態磁滯模型的有限元計算中，固定點迭代方法已經取得了較好的收斂效果與計算速度[24-26]，并已在目前的商業軟件中取得了較好的計算效果。然而，在引入渦流損耗磁場與剩余損耗磁場后，收斂將難以得到保證，特別是在計算至磁通密度零點附近時間步時算法極易發散，分析其原因主要是渦流損耗、剩余損耗等效動態磁場的介入改變了固定點法中磁通密度與磁場強度的收斂過程，使得傳統微分磁阻率的定義無法準確描述收斂路徑的斜率，計算得到微分磁阻率過低導致考慮動態磁滯效應的有限元方程求解不收斂。

為解決在考慮動態磁滯特性的時域有限元計算難以收斂的問題，本文提出一種基于等效磁阻率的固定點迭代求解策略，進而提出一種耦合動態磁滯特性的時步有限元分析方法。首先，為了獲得電工鋼片的動態、靜態磁滯特性，基于愛潑斯坦方圈法搭建了一維磁特性測量系統；其次，考慮到逆Preisach模型可以考慮磁化歷史具有較高的計算精度，同時在耦合有限元計算時易于數值實現的特點，本文構建了基于參數化解析一階回轉曲線的逆 Preisach模型，并進行了參數辨識；再次，分析了渦流損耗和剩余損耗對算法收斂特性的影響，提出基于等效磁阻率的固定點迭代策略，并在有限元迭代過程中加入松弛因子保證穩定性；最后，以愛潑斯坦方圈為例，進行了考慮動態磁滯效應的時域有限元分析，求解了瞬時功率損耗特性，并進行了實驗對比驗證。結果驗證了本文所提方法的準確性、高效性與穩定性。

1 準靜態與動態磁滯特性測量

為建立磁滯模型及驗證有限元計算準確性，基于 IEC 60404—2 標準建立了一維磁性能測量平臺，對牌號為B30P105 的取向硅鋼片進行準靜態與動態磁滯特性測量。電工鋼片一維磁特性測量平臺如圖1 所示，該平臺包括寬頻功率放大器、電壓前置放大器、愛潑斯坦方圈、多功能數據采集卡和 LabVIEW 控制系統。本實驗采用的硅鋼片規格及測試條件見表1。分別設定正弦交流電壓激勵的頻率為5 Hz 與50 Hz，測量得到準靜態磁滯回線和50 Hz 動態磁滯回線，結果如圖2 和圖3 所示。

表1 硅鋼片規格及測試條件Tab.1 Specifications and test conditions of silicon steel sheets

圖1 電工鋼片一維磁特性測量平臺Fig.1 Measuring platform for 1-D magnetic propertiesof electrical steel sheets

圖2 5 Hz 準靜態磁滯回線測量結果Fig.2 Measured quasi-static hysteresis loop (5 Hz)

圖3 50 Hz 動態磁滯回線測量結果Fig.3 Measured dynamic hysteresis loop (50 Hz)

2 靜態逆Preisach 磁滯模型的構建

本文采用離散形式的靜態逆Preisach 磁滯模型描述硅鋼片的磁滯特性，該模型采用一種一階回轉曲線（First Order Reversal Curves, FORCs）的解析計算方法，并基于少量準靜態磁滯回線測量數據實現解析式的參數辨識，從而構造出辨識逆Everett 函數所需的一階回轉曲線，并進一步建立靜態逆Preisach 磁滯模型。解析一階回轉曲線構造示意圖如圖4 所示：一條起始于準靜態極限磁滯回線下降支的一階回轉曲線R-P-N-T，該曲線起點為回轉點R，極限磁滯回線上升支Ha和下降支Hd交匯于頂點T。該一階回轉曲線構造時需首先確定極限磁滯回線在回轉點R 處寬度ΔHrev和R 點與T 點的垂直高度ΔBrev為

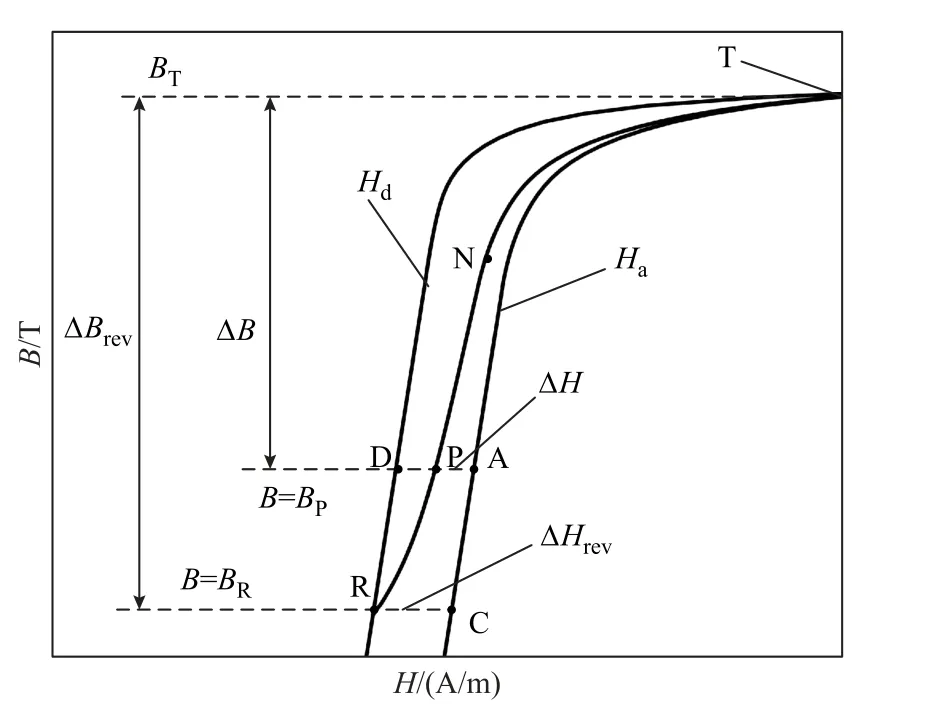
圖4 解析一階回轉曲線構造示意圖Fig.4 Construction ofanalytical first order reversal curve

圖4 中一階回轉曲線上點P 所在磁通密度為BP，磁場強度HP的計算式為

式中，ΔHout為極限磁滯回線在高度為BP處的寬度；x表征不同的P 點在一階回轉曲線上的相對位置，定義為

a、b、c為待擬合的模型參數。當滿足a＞0，0＜b＜1，c＞0 等條件時，可使得一階回轉曲線斜率始終為正且不會超出最大極限磁滯回線。同時，以上模型參數與回轉點R 在下降支上的位置有關，此處定義位置系數β為

式中，ΔBout為最大環磁滯回線的高度。

參數a、b、c可表示為β的多項式，即

式中，y為多項式系數向量。

以上多項式系數通過準靜態磁滯回線測量數據進行辨識，由于對稱性，辨識過程僅需要磁滯回線的上升支。逆Everett 函數值可利用上升支一階回轉曲線Hforc通過式（7）計算。

磁通密度幅值為Bm的同心磁滯回線上升支可通過逆Everett 函數進行插值運算得到。

辨識程序中一共使用9 條磁滯回線，將每條磁滯回線上升支根據磁通密度均勻等分為50 個點。基于式（7）、式（8）可得到由一階回轉曲線計算磁滯回線的數值關系，進而建立適應度函數F為

式中，Hmeas、Hcal分別為磁滯回線磁場強度的測量值和計算值；Bki為辨識程序中第k條磁滯回線上第i個點的磁通密度值。采用遺傳算法基于適應度函數進行參數尋優，結果見表2。獲得全部參數后，采用該解析式模擬所需一階回轉曲線數據，進一步可計算逆Everett 函數E(bu,bv)，通過解析一階回轉曲線辨識的逆Everett 函數如圖5 所示。

表2 B30P105 型電工鋼片多項式參數辨識結果Tab.2 The identified polynomial parameters of B30P105 elctrical steel sheet

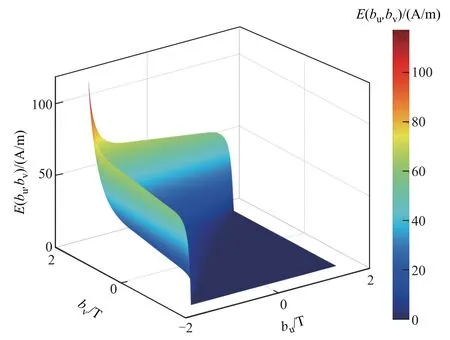
圖5 通過解析一階回轉曲線辨識的逆Everett 函數Fig.5 Inverted Everett functionidentified by analytical first order reversal curves

通過上述逆Everett 函數辨識結果，可計算出一個周期內不同磁通密度下電工鋼片的靜態磁滯回線。B30P105 型取向硅鋼的準靜態磁滯回線實驗結果和模型計算結果對比如圖6 所示，可以看出，本文所構建的逆Preisach 磁滯模型具有一定的全局意義，可準確模擬不同磁通密度幅值下的準靜態磁滯回線，為進一步考慮動態磁滯特性的有限元計算提供了可靠的模型基礎。

圖6 準靜態磁滯回線測量值與計算值對比Fig.6 Comparison between measured and calculated quasi-static hysteresis loops

3 考慮動態磁滯特性的時域有限元方法

3.1 動態磁場的表征方法

Bertotti 基于磁疇理論和統計學原理提出損耗分離理論，將鐵磁材料單位體積的總損耗Ptot分為磁滯損耗Phys、渦流損耗Peddy和異常損耗Pexc三項。即

式中，σ為材料的電導率；d為硅鋼片厚度；S為橫截面積；G為無量綱耦合常數，G=0.135 6；V0為與材料內部磁性單元有關的統計參數，同磁通密度幅值Bm相關，可通過不同頻率下的磁滯回線實驗數據擬合得到。

磁場損耗W與B、H之間的關系為

將式（11）代入式（10）可得動態磁場表達式為

式中，Htot、Hhys、Heddy、Hexc分別為動態磁場總磁場強度、靜態磁滯磁場強度、渦流磁場強度、異常磁場強度；δB為符號函數，δB=sign(dB/dt)=±1。然而，由于較強的非線性特征，上述磁場難以直接在有限元分析中進行迭代耦合計算，需進一步研究其有限元迭代形式。

3.2 動態磁滯特性在有限元中的直接耦合形式

基于后向差分法，總磁場強度的三個分量的時域離散形式為

式中，t為時間步；Δt為步長間隔；vh為靜態磁滯微分磁阻率，定義為

相關麥克斯韋磁場方程為

結合方程式（13）～式（19）可得基于矢量磁位A的控制方程為

式中，ve為等效磁阻率，表達式為

3.3 基于等效磁阻率的固定點迭代策略

固定點法通過將非線性磁滯關系分為線性和非線性兩部分，通過在迭代過程內不斷修改非線性部分以達到收斂，在解決磁滯非線性問題中具有較好的收斂性。為此，本文考慮將固定點迭代技術引入考慮動態磁滯特性的有限元迭代過程之中，在考慮靜態磁滯特性的基礎上，引入考慮動態磁場分量影響的等效磁阻率，采用式（21）中等效磁阻率代替傳統固定點法的微分磁阻率vFP。應用固定點技術，總磁場強度Htot和磁通密度B的非線性關系可表示為

式中，R為類磁化余量。

結合麥克斯韋方程，可得控制方程為

在二維求解域Ω中，將方程式（23）展開為離散形式為

式中，N為離散單元的基函數。將方程式（24）改寫為矩陣形式，即

式中，S為剛度矩陣；A為磁矢位向量；Y為電流區域系數向量；I為繞組電流向量；G為余量R的旋度矩陣。該方法中，渦流損耗等效磁場和剩余損耗等效磁場表達在類磁化余量R的計算中。通過這種方式，不需要大幅改動有限元方程，使得算法流程更簡潔，同時，將動態特性考慮在余量中，便于在以后的工作中對渦流和剩余損耗計算模型的改進與修正。而且，在每一時刻的迭代過程，僅需計算一次等效磁阻率ve和剛度矩陣S，顯著提升了計算效率。

為保證固定點算法收斂，磁阻率v應滿足式（26）的必要條件[25,27]。

在傳統固定點法中，所有網格單元采用統一的磁阻率，即

式中，vmin、vmax分別為磁滯回線上斜率最小值與最大值。該方法稱為GCM（global-coefficient method）。顯然，采用式（27）計算的磁阻率總能滿足算法收斂的必要條件。然而，GCM 采用統一的磁阻率導致計算時間過長，需采用更具效率的微分磁阻率進行迭代，微分磁阻率vFP定義為

式中，dHtot、dB分別為磁場強度和磁通密度的差分。

對于標量磁滯模型，二維電磁場量間的關系可通過取模值降階為一維問題。如圖7 所示，藍色實線表示靜態磁滯回線，藍色虛線表示動態磁滯曲線，曲線L 為固定點迭代過程中動態磁滯磁場Htot與磁通密度B的軌跡。由于磁場分量Heddy、Hexc的計算是基于磁通密度B的后向差分對時間的偏導數，因此，該曲線L 起始于t時刻靜態磁滯回線上的點P1，止于t+1 時刻動態磁滯回線上點P3。顯然，由于渦流損耗和剩余損耗的影響，曲線L 的斜率明顯不同于動態磁滯回線的斜率，在磁通密度的零點附近，兩者相差很大。傳統的固定點迭代法采用式（28）來計算微分磁阻率vFP，由于只考慮到動態磁滯磁場的軌跡，其計算結果偏小，往往不滿足收斂的必要條件，在迭代計算中算法極易發散。相反，在本文所提式（21）中等效磁阻率ve的計算考慮了渦流損耗和剩余損耗的等效磁場，反映了鐵心動態磁滯損耗對迭代過程的影響大小，可準確估計動態B-Htot軌跡L 的斜率，從而保證迭代過程穩定收斂。在有限元程序中ve根據前兩個時間點的結果進行估算，即

圖7 動態磁滯收斂路徑示意圖Fig.7 Schematic diagramof dynamic hysteresis convergence path

3.4 考慮動態磁滯特性的場-路耦合有限元分析

鑒于電機、變壓器等大多數電氣設備工作于50 Hz正弦交流電壓激勵下，為反映動態磁場和電壓源的相互作用，需在時域有限元分析中進行“場-路”耦合。由于愛潑斯坦方圈實質可看作一臺等比的空載變壓器，可以滿足對變壓器鐵心損耗分析的需要。為驗證本文所提方法的有效性，本文以愛潑斯坦方圈為例構建了二維有限元計算模型。

在模型的計算過程中，以50 Hz 正弦交流電壓作為激勵，從電路角度分析，不考慮勵磁線圈漏磁和匝間電容，則端口電路方程為

式中，U為激勵電壓；Uin為繞組上的感應電動勢；r為線路電阻；I為勵磁電流。對于一階三角形單元，Uin的計算式為

式中，Φ為繞組磁通；Nc為線圈匝數；Sc為繞組截面積；Ωc為電流區域；se為單元面積；lz為二維求解系統縱向深度；Ae為單元節點磁矢位。將式（31）代入式（30）得到

式中，U為激勵電壓向量；r為支路電阻矩陣。采用Crank-Nicolson 差分格式，將式（25）、式（32）聯立求解。

通過求解方程式（33）得到磁矢勢向量，然后根據B=?×A計算出每個單元的磁通密度大小。如果計算結果未達到收斂條件eB=∣Bi+1-Bi∣＜Bε（相對殘差閾值一般取εB= 1× 1 0-5），則通過磁滯模型計算靜態磁滯磁場Hhys、渦流磁場Heddy、剩余損耗磁場Hexc，進而計算總磁場強度Htot，并通過松弛因子λ對Htot進行修正。

式中，i為迭代次數。若磁通密度B相鄰迭代誤差滿足收斂條件，則判斷是否達到最大時間步，若t=tmax，則停止迭代，輸出全部計算結果，否則跳轉至下一時間步。整個有限元迭代過程如圖8 所示。

圖8 考慮動態磁滯特性的有限元分析流程Fig.8 Finite element iterative calculation process considering dynamic hysteresis characteristics

需要說明的是：不同于靜態磁滯磁場，動態磁場強度和磁通密度間的非線性關系不是一開始就確定的，由于渦流磁場和剩余損耗磁場不是直接通過有限元磁場方程表達，而是在固定點迭代過程加入，這意味著在算法迭代過程中，非線性磁場關系不斷改變，由動態磁場分量帶來的數值擾動使得磁矢位A和磁通密度B計算結果變化劇烈，造成收斂困難，尤其在磁通密度的零點附近，dB/dHtot較大，磁場強度的計算誤差引起的數值振蕩更大。因此松弛因子λ的引入是十分必要的。

4 結果與討論

4.1 愛潑斯坦方圈動態磁滯回線有限元模擬

為說明本文所提方法的有效性，在計算模型中，選取了愛潑斯坦方圈臂上的三角形單元作為磁滯回線與損耗的觀測點，其二維網格剖分情況如圖9 所示，三角網格M 為進行實驗數據與模型計算數據的對比的參考單元。在50 Hz 正弦條件下，圖10a、圖11a 分別給出了激勵電壓幅值為Umax=9 V 和Umax=13 V 時M 單元處磁滯回線測量值與計算值的對比。可以看出，再考慮動態磁滯特性后，本文所提方法具有較高的磁滯回線模擬精度。進一步地，圖10b、圖11b 給出了相應電壓激勵條件下愛潑斯坦方圈勵磁電流波形的模擬結果。由于考慮了動態磁場與磁滯效應對電流波形的反饋作用，本文所提方法可以較好地模擬勵磁電流時域波形。

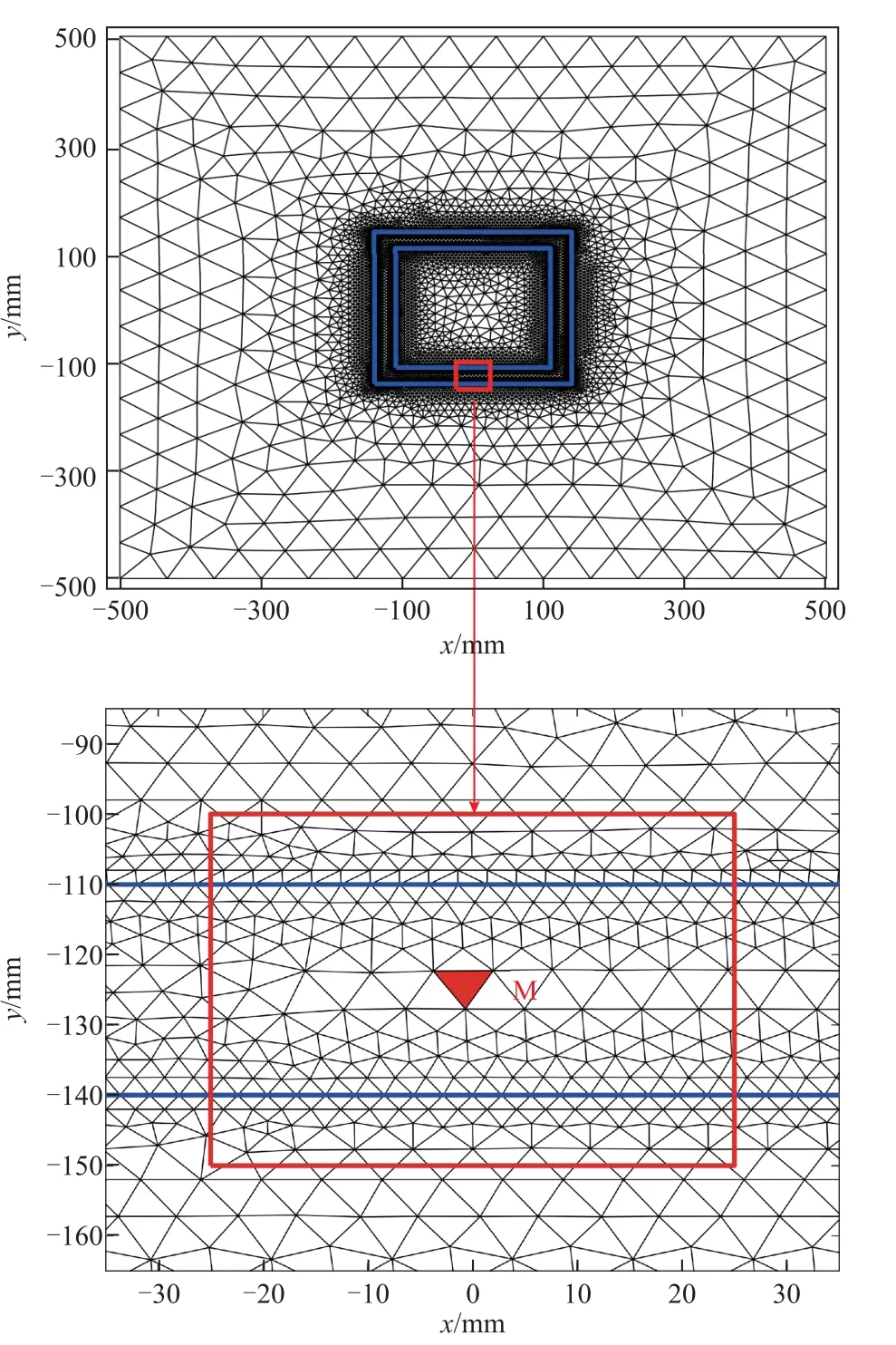
圖9 愛潑斯坦方圈有限元剖分Fig.9 Finite element mesh of Epstein frame

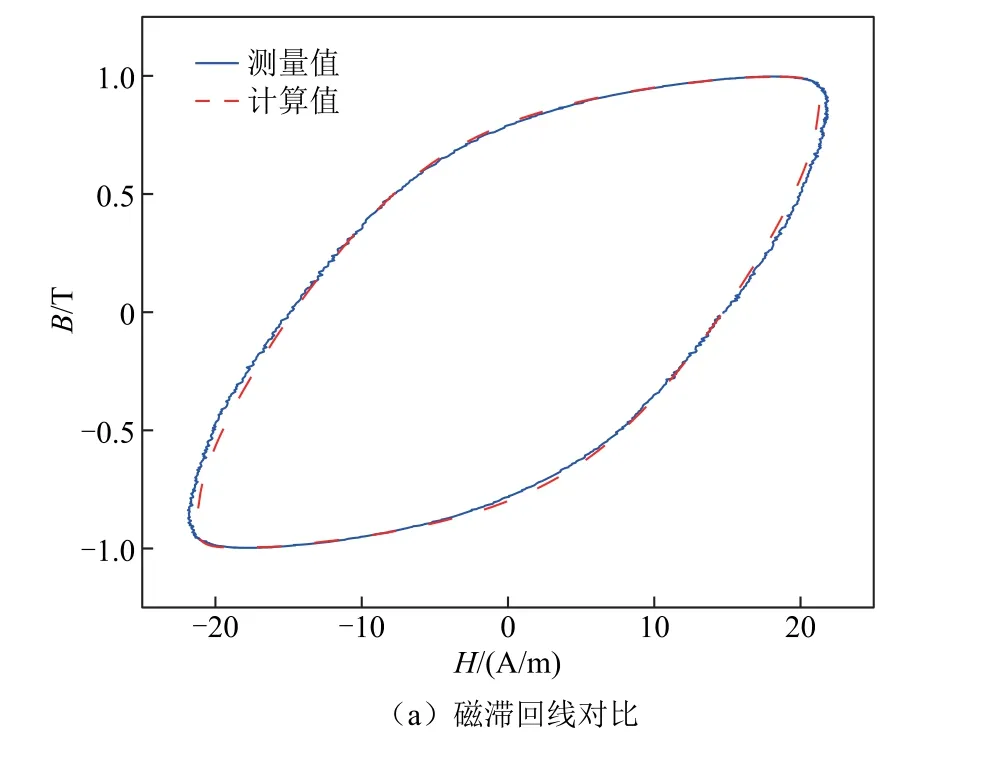
圖10 Umax=9 V 電壓激勵下測量值與計算值對比Fig.10 Comparison between measured and calculated values under voltage excitation Umax=9 V

圖11 Umax=13 V 電壓激勵下測量值與計算值對比Fig.11 Comparison between measured and calculated values under voltage excitation Umax=13 V

為考察松弛因子λ對程序收斂性的影響，控制電壓激勵分別為Umax=9 V，調節松弛因子大小，記錄程序是否收斂，以及程序收斂情況下一周期內的平均迭代次數和程序總計算時間。結果見表3，當λ=0.8時，有限元迭代過程不收斂，在確保收斂的情況下，采用較大的松弛因子可減少每時步的平均迭代次數和總計算時間，提升計算效率，最短總計算時間為228 s。通常，為同時滿足穩定性和計算速度的要求，設置λ=0.5～0.7 即可。

表3 9 V 電壓激勵時不同松弛因子對迭代次數和總迭代時間影響Tab.3 Effects of different relaxations on the iterations and computation time with voltage excitation amplitude of 9 V

4.2 磁通密度分布與瞬時損耗特性

為進一步檢驗算法的有效性，本文對愛潑斯坦方圈的磁通密度分布特性與瞬時功率損耗特性進行了分析與計算。在t=0.005 s 時的磁通密度分布計算結果如圖12 所示。可以看出，主磁路上磁通密度分布較為均勻，側壁上磁通密度幅值計算結果與實驗測量值基本一致；而在疊片的內角處，磁通密度較大，在外角部分磁通密度較小。

圖12 磁通密度分布（Umax=13 V、t=0.005 s）Fig.12 Distribution of magnetic flux density (Umax=13 V、t=0.005 s)

根據4.1 節中磁通密度B和動態磁場Htot計算結果，本文進一步計算了Umax=9 V 和Umax=13 V 兩種激勵大小在參考單元M 處一周期內的瞬時損耗功率tp并與測量值進行對比，結果如圖13 所示。在t=0.00 2 s 和t=0.012 s 附近，測量與計算的瞬時損耗達到極大值；在t=0.005 s 和t=0.015 s 附近，瞬時損耗達到極小值。損耗負值來源于可逆磁化的貢獻。可以看出，本文所提方法在模擬瞬時功率方面具有較高的精度，瞬時損耗的最大誤差不超過6%。

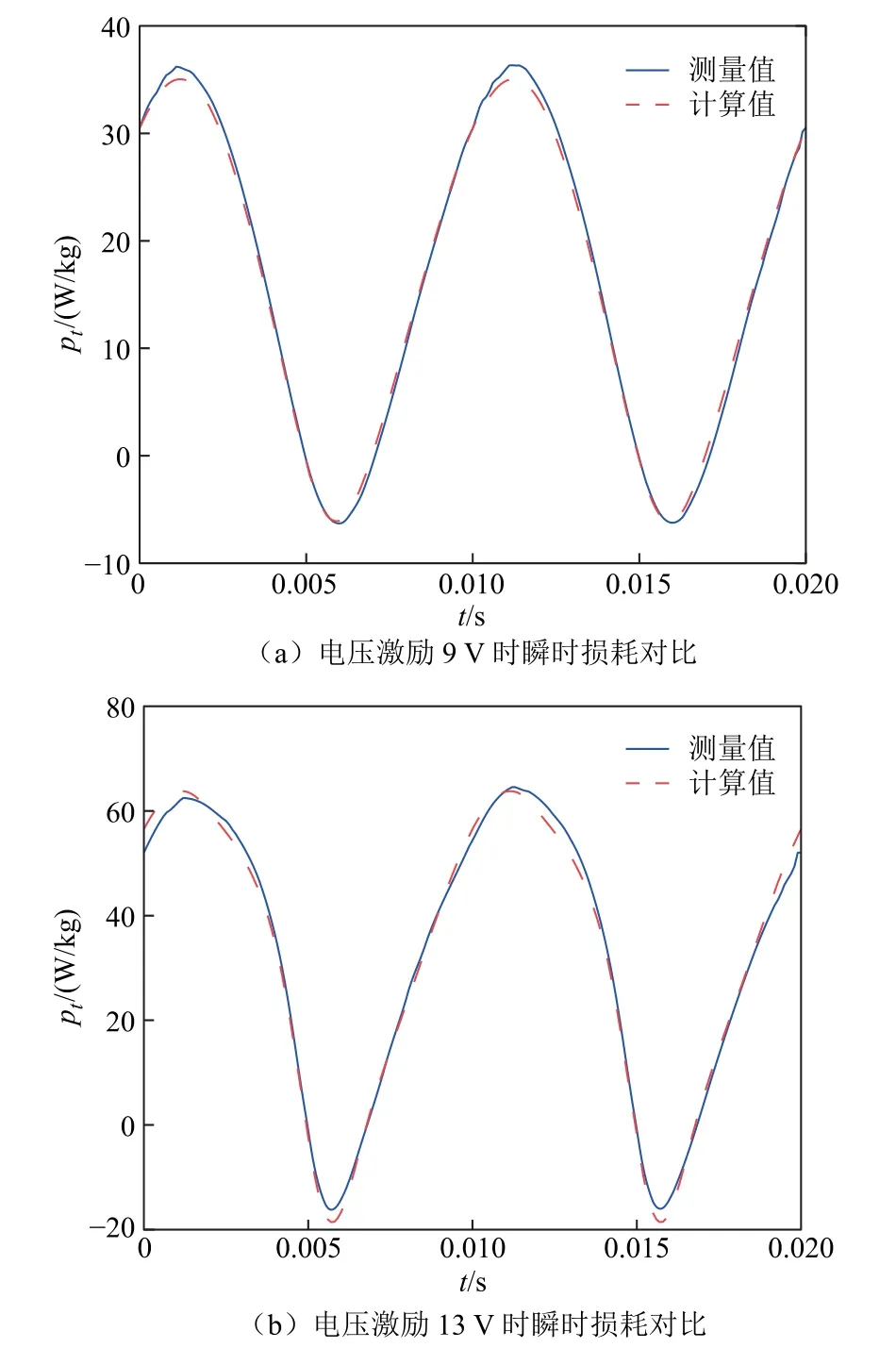
圖13 動態磁滯瞬時損耗測量值與計算值對比Fig.13 Comparison between measured and calculated instantaneous loss when considering dynamic hysteresis

完成一個周期有限元計算后，積分得到每一個單元磁滯回線的面積并求和即可得到鐵心區域整體鐵心總損耗PFe為

式中，f為激勵的頻率；ne為鐵心離散單元總數。圖14 所示為不同磁通密度幅值時的鐵心總損耗計算值和測量值大小。可以看出，通過提出的有限元算法計算得到的一個周期內的鐵心損耗與實驗測量結果基本一致。

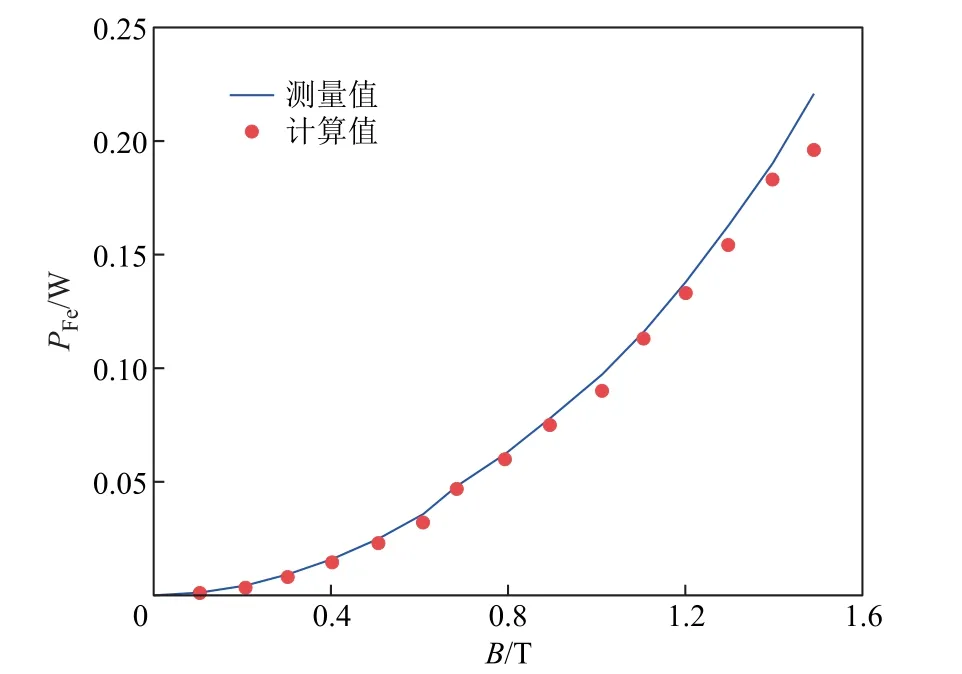
圖14 鐵心損耗測量值與計算值對比Fig.14 Comparison between measured and calculated power losses

5 結論

為解決時域有限元分析中考慮鐵心材料的動態磁滯特性出現難以收斂的問題，本文提出了一種基于等效磁阻率的高效穩定改進固定點迭代策略，并編寫了相應的有限元程序，實現了硅鋼片的動態磁滯特性進行模擬計算，并通過實驗測量結果對比，驗證了該有限元算法的有效性與準確性，具體貢獻如下：

1）采用解析方法生成一階回轉曲線，辨識逆Everett 函數，建立逆Preisach 磁滯模型，可準確模擬電工鋼片靜態磁滯特性。

2）采用固定點迭代技術耦合動態磁滯特性，通過分析渦流損耗和剩余損耗等效磁場對有限元迭代過程的影響，提出基于等效磁阻率的固定點策略，并在有限元迭代過程引入松弛因子，通過實驗數據與計算結果的對比分析，驗證了本文提出的方法可實現低頻動態磁滯磁場的準確計算，并具有良好的計算速度和穩定性。

3）通過場-路耦合有限元算法與動態磁滯模型結合，可充分考慮鐵心總損耗對電路和磁場的反饋效應，實現瞬時損耗的準確計算，最大計算誤差不超過6%，可滿足工程計算要求。