“鱉臑”鬧課堂
——“鱉臑模型的應用及探究”教學實錄

陳秋月 汪庭斌

(安徽省寧國中學)

數學文化類試題是近幾年高考試題中的熱點問題,教師應積極挖掘教材中的數學文化素材,巧妙融合數學知識,融會數學思想方法,發揮數學文化的育人作用.本節課借助鱉臑模型的應用與探究,為學生提供自由表達、質疑、探究、討論問題的機會,讓學生感受數學文化的魅力、數學學習的快樂,讓數學學科核心素養在教學中全方位滲透.

1 高考題中的鱉臑

例1 (2015年湖北卷文20)?九章算術?中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑.如圖1所示,在陽馬P-ABCD中,側棱PD⊥底面ABCD,且PD＝CD,點E是PC的 中 點,連 接DE,BD,BE.

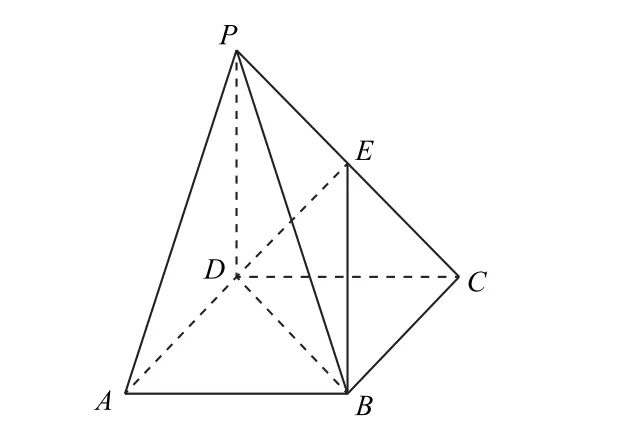
圖1

(1)證明:DE⊥平面PBC,試判斷四面體EBCD是否為鱉臑,若是,寫出其每個面的直角(只需寫出結論);若不是,說明理由;

(2)記陽馬P-ABCD的體積為V1,四面體E-BCD的體積為的值.

設計意圖 柏拉圖說:“良好的開端,是成功的一半.”在課堂情境的設置中,筆者以一道高考試題拋磚引玉,題中的“陽馬”“鱉臑”引起學生的關注,充分調動大家的學習興趣,為后面模型來源、應用和探究的層層遞進,螺旋式上升做好鋪墊.

2 鱉臑的來源

鱉臑是我國古代數學中非常重要的模型,在多本著作里都有闡述.

?九章算術?中記載“斜解立方,得兩塹堵.斜解塹堵,其一為陽馬,一為鱉臑.陽馬居二,鱉臑居一,不易之率也.合兩鱉臑三而一,驗之以棊,其形露矣.”東晉時期著名數學家劉徽說到“此術臑者,背節也,或曰半陽馬,其形有似鱉肘,故以名云.中破陽馬,得兩鱉臑,鱉臑之起數,數同而實據半,故云六而一即得.”

師生共同觀看視頻——鱉臑的生成過程.

設計意圖 用動態的視頻生動形象地演示出中國古代數學文化中的塹堵、陽馬、鱉臑的生成.塹堵、陽馬、鱉臑實際上是中國古代對一些特殊幾何體的稱呼,通過視頻的播放讓學生更直觀地感受到“陌生”的鱉臑實際上是我們再熟悉不過的立體幾何體.

3 鱉臑的定義

師:同學們,現在知道了塹堵、陽馬和鱉臑的來源了,那么如何準確地定義它們呢?

小組熱烈討論交流,給出了它們的定義.

生:塹堵是兩底面為直角三角形的三棱柱.

生:陽馬是底面為長方形,兩個三角面與底面垂直的四棱錐體.

生:鱉臑是四個面都為直角三角形的三棱錐.

師:同學們描述得很準確,它們實際上都是我們熟悉的幾何體(如圖2).

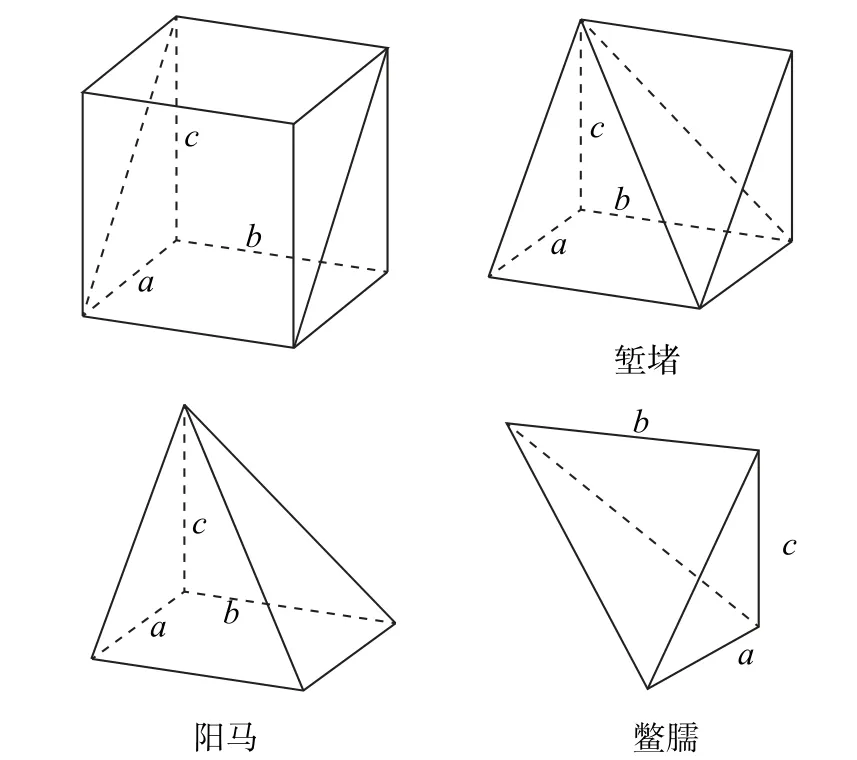
圖2

設計意圖 從動態的視頻中提煉出塹堵、陽馬、鱉臑的靜態圖形,以便學生更細致地觀察、認識、探究,抓住它們的幾何特征,給出精準的定義.

4 教材中的鱉臑

例2 (人教A 版數學必修第二冊第158頁例8)如圖3所示,AB是圓O的直徑,PA垂直于圓O所在的平面,C是圓周上不同于A,B的任意一點,求證:平面PAC⊥平面PBC.

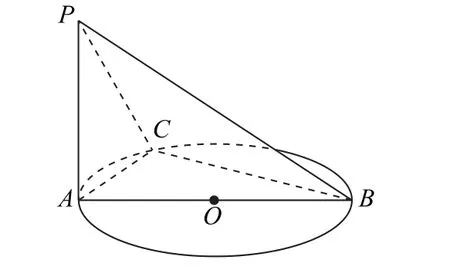
圖3

師:請同學們仔細觀察一下三棱錐P-ABC,發現它有什么幾何特征嗎?

生:它的四個面都是直角三角形,它是鱉臑.

師:回答得非常好,三棱錐P-ABC就是鱉臑模型.

大家再觀察一下,鱉臑還有其他等價的定義嗎?

生:三棱錐中一側棱與底面垂直,底面為直角三角形.

師:精準嗎?

生:側棱應該垂直于底面銳角頂點處.

師:非常棒!

例3 (人教A 版數學必修第二冊第158 頁練習3)如圖4 所 示,AB⊥平 面BCD,BC⊥CD,你能發現哪些平面互相垂直,為什么?

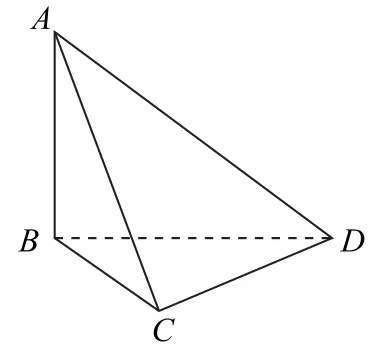
圖4

三棱錐A-BCD也是鱉臑,更進一步深化了對鱉臑模型的認識.

設計意圖 挖掘教材中文化資源,以課本上的例題和練習題為載體,引導學生進行探究,發現規律,深化學生對鱉臑模型的認識,體驗數學文化,也為下一步學生自主探究做好鋪墊.

5 鱉臑的深度探究

追問1:如何判斷一個三棱錐A-BCD是鱉臑呢?

生:定義法,它是四個面都為直角三角形的三棱錐.

師:很好,還有嗎?

生:AB,CD,BC兩兩垂直.

生:AB⊥平面BCD,且BC⊥CD.

生:AB⊥平面BCD,將BC⊥CD改成AC⊥CD也可以.

生:AB⊥平面BCD,且平面ABC⊥平面ACD.

師:同學們歸納總結得特別好、特別全面,這些都可以證明,若三棱錐A-BCD的四個面都是直角三角形,則它是鱉臑.

師:在鱉臑模型中有著求解立體幾何問題的核心關系——垂直關系.

追問2:在上述鱉臑幾何體的棱和面中,有哪幾組線線垂直、線面垂直、面面垂直呢?

生:線線垂直中相交垂直有四組:AB⊥BD,AC⊥CD,AB⊥BC,BC⊥CD;異面垂直的只有一組:AB⊥CD.

生:線面垂直有兩組:AB⊥平面BCD,CD⊥平面ABC.

生:面面垂直有三組:平面ABC⊥平面ACD,平面ABC⊥平面BCD,平面ABD⊥平面BCD.

師:同學們太棒了,大家總結的這些垂直關系都是鱉臑的豐富性質.

設計意圖 通過一連串的追問,引導學生借助鱉臑這一幾何體中豐富的(線線、線面、面面)垂直關系,讓學生熟悉垂直關系下的定理和性質的應用,充分發揮課本習題的教育功能和教學價值.

6 鱉臑模型的應用

師:同學們,2015年湖北卷文科試題就以鱉臑作為命題的背景(例1),引起了廣泛關注,當年很多學生沒見過這兩個字,因此影響了答題的心情.今天我們已經了解并掌握了鱉臑的定義和性質,我們應該有信心解決這道高考題.

生:要證線面垂直,只需證線線垂直.因為PD⊥底面ABCD,所以PD⊥BC,又底面ABCD是長方形,得CD⊥BC,而PD∩CD＝D,所以BC⊥平面PCD.又DE?平面PCD,所以BC⊥DE.

因為點E是PC的中點,且PD＝CD,所以DE⊥PC.而PC∩BC＝C,所以DE⊥平面PBC.

由DE⊥平面PBC,DE?平面PCD,可知四面體EBCD的四個面都是直角三角形,即四面體EBCD是鱉臑,其四個面的直角分別是∠BCE,∠BCD,∠DEB,∠DEC.

師:證明得非常嚴謹、規范,對陽馬和鱉臑這兩個模型掌握得非常好,那第(2)問誰來挑戰一下?

設計意圖 這是一道與陽馬、鱉臑模型有關的高考題,體現了新課程要重視數學文化這一重要基本理念.高考中對數學文化的考查要求,也顯示出數學文化在高考試題中獨特的地位.在問題的探究中,學生更加熟習立體幾何體中的垂直關系、定理和性質的應用.

7 課后作業

1)回歸課本

人教A 版數學必修第二冊中有許多相關問題.

1.(第160頁例10)如圖5所示,已知PA⊥平面ABC,平面PAB⊥平面PBC,求證:BC⊥平面PAB.

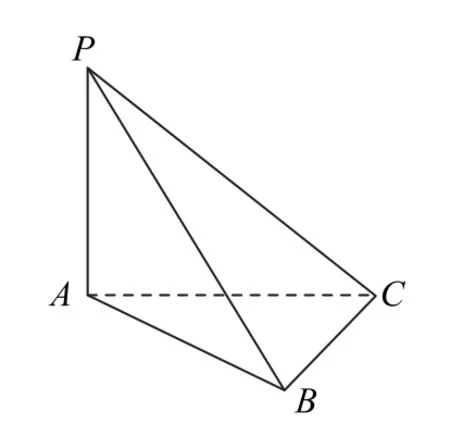
圖5

2.(第164 頁第20題)如圖6 所 示,AB是 圓O的直徑,點C是圓O上的動點,過動點C的直線VC垂直于圓O所在平面,D,E分別是VA,VC的中點.判斷直線DE與平面VBC的位置關系,并說明理由.

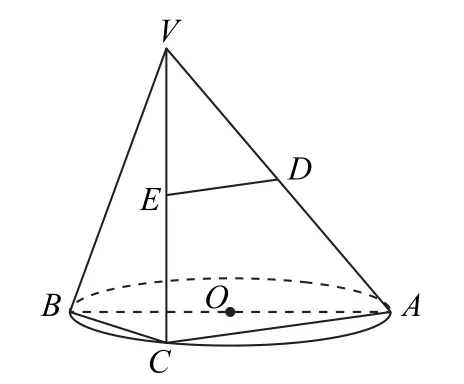
圖6

3.(第170頁第9題)如圖7所示,在三棱錐P-ABC中,PC⊥底面ABC,AB⊥BC,D,E分別是AB,PB的中點求證:

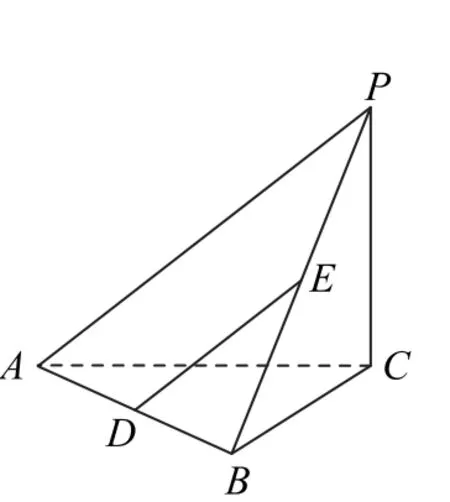
圖7

(1)DE//平面PAC;

(2)AB⊥PB.

4.(第171頁 第13題)如圖8 所示,在三棱錐P-ABC中,∠ACB＝90°,PA⊥底面ABC.

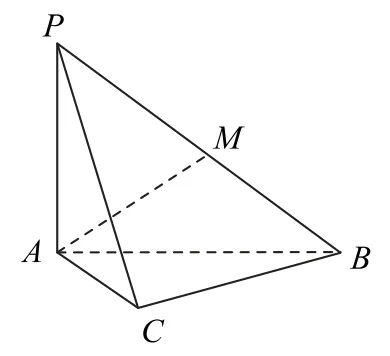
圖8

(1)求證:平面PAC⊥平面PBC;

(2)若AC＝BC＝PA,M是PB的中點,求AM與平面PBC所成角的正切值.

2)課后拓展

如圖9所示,PA⊥圓O所在的平面,AB是圓O的直徑,C是圓周上一點,其中AC＝3,PA＝4,BC＝5.

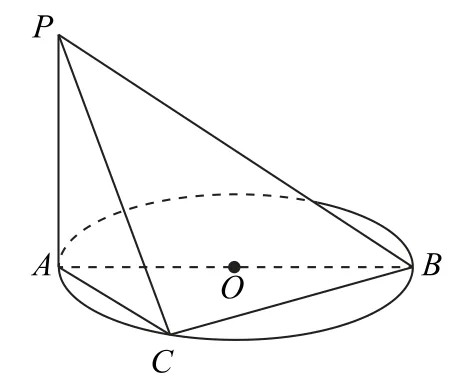
圖9

(1)求PB與平面PAC所成角的正弦值;

(2)求該幾何體的外接球的半徑;

(3)求該幾何體的內切球的半徑.

設計意圖 這些題目都是鱉臑模型,相當于設置了“微專題”,對所學的知識和應用起到鞏固和強化的效果,同時又布置了課后拓展題,求鱉臑模型中的線面角及外接球和內切球的半徑,這也是為鱉臑模型下一步的延伸拓展探究做鋪墊.

本節課中通過鱉臑模型的導引對高考題中的鱉臑、教材中的鱉臑進行了探究,在探究的過程中,通過對鱉臑模型的觀察、發現、探索、實踐揭示了鱉臑模型的本質.通過鱉臑模型這一載體挖掘了立體幾何中線線垂直、線面垂直、面面垂直以及三種垂直關系的相互轉化,更加熟練地使用判定定理和性質,提升學生思維能力和解題能力.將數學文化融入課堂教學中,得到了學生的認可,大大激發學生探究立體幾何的熱情,教師的教和學生的學融為一體,我們的課堂也因此更加精彩,創造真正高效、高質量、靈動的課堂.

(完)