一道高考題的解法與拓展

張露梅 何拓程(特級教師)

(1.中央民族大學附屬中學 2.北京理工大學附屬中學)

高考題是命題專家精心命制的,充分體現了數學學科核心素養,蘊含了豐富的數學思想,具有很高的信度和效度.挖掘高考試題的數學教育價值,并提出具有探究性的問題,引導學生開展探究活動,使學生在掌握知識的同時學會研究,提高其發現問題、分析問題和解決問題的能力,以達到進一步理解數學的目的.本文以2020年高考數學北京卷第20題為例,進行一些探討.

1 原題再現

(1)求橢圓C的方程;

(2)過點B(－4,0)的直線l交橢圓C于點M,N,直線MA,NA分別交直線x＝－4于點P,Q,求的值.

2 解法探究

分析 第(1)問,根據條件列出a,b,c的關系式,從而求出橢圓的標準方程.第(2)問,要求的值,等價于求,因此需要由直線MA,NA的方程確定點P,Q的縱坐標.

(2)如圖1 所示,設M(x1,y1),N(x2,y2),P(－4,yP),Q(－4,yQ),MB的斜率為k,則直線l的方程為y＝k(x＋4),MA的方程為

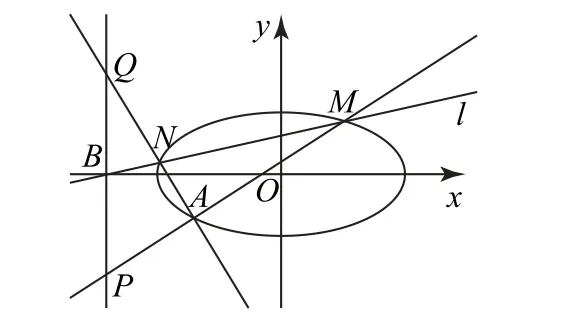
圖1

令x＝－4,可得

如果充分研究幾何條件并將其代數化(坐標化),同樣得到這樣的結論.過點A作垂直于x軸的直線m與直線l相交于點T(如圖2),利用三角形相似可將豎直方向的比值轉化為水平方向的比值.

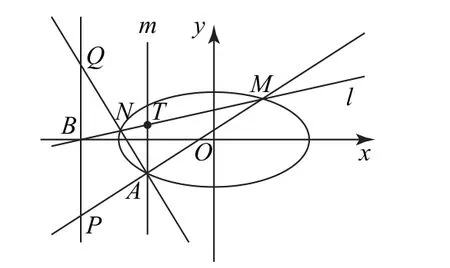
圖2

設T(－2,yT),則

可得

由于出現了4x2＋2x1,4x1＋2x2,即x1,x2的系數不均衡的情況,無法直接運用根與系數的關系,解題出現了困境,如何突破難點?

探究1 “湊”根與系數的關系,分而治之

由題可知直線l的斜率必存在,設斜率為k,則直線l的方程為y＝k(x＋4),與橢圓方程聯立,可得(4k2＋1)x2＋32k2x＋64k2－8＝0,由

基于消元思想,利用根與系數的關系,將這個比值轉化為只含一個根和斜率k的式子,這種方法雖然計算量較大,但是思維量較小,是必須掌握的通性通法.

探究2 “用”根與系數的關系,整體代換

同探究1,可得

消去k2可得

探究3 “審”原題條件,特值引路

顯然yPyQ＜0,取MN斜率為零的特殊情況,可以求出比值為1,即,因此轉化為證明yP＋yQ＝0,即可直接利用根與系數的關系.

同探究1,可得

其中

從而yP＋yQ＝0,所以.這里要求學生有很強的審題意識,充分挖掘題目內在的聯系,同時對學生的思維能力也有較高的要求.

3 還有話說

3.1 變換題設條件與結論

將上述高考題中第(2)問變成:過點B(m,0)的直線l交橢圓C于點M,N,直線MA,NA分別交直線x＝m于點P,Q,若,求m的值.

設M(x1,y1),N(x2,y2),由探究3,先用特值引路,取MN斜率為零的特殊情況,因為

解出m＝－4.

一般地,設直線MN的斜率為k,則直線MN的方程為y＝k(x－m),與橢圓方程聯立可得

當Δ＝(－8mk2)2－4(4k2＋1)(4m2k2－8)＞0時,可得k2(m2－8)－2＜0,此時方程有兩個不相等的實根,則

又直線MA的方程為

令x＝m,則

同理,有

所以yP＋yQ＝(m＋4)[－4k(m＋2)＋4]＝0恒成立,故m＝－4.

3.2 拓展題目的結論

再將上述高考題中第(2)問變成:過點B(m,0)的直線l交橢圓C于點M,N,直線MA,NA分別交直線x＝m于點P,Q,若,探求m與λ的關系.

設M(x1,y1),N(x2,y2),先用特值引路,取MN斜率為零的特殊情況,因為

所以

顯然,當λ＝1時,即為3.1中的問題.

另外,由上式知λ≠(2＋1)2,感興趣的讀者可以嘗試思考一下,當λ＝(2＋1)2時是什么樣的情形.

4 我的思考

4.1 理解數學,突出本質

數學的本質是從變化的數學對象中探求不變的性質,理解數學要從理解數學的本質開始.本題第(2)問不落俗套地選擇不能直接運用根與系數的關系來考查學生探究能力,很好地考查了學生的數學素養.數學素養就是對數學本質的理解和把握.學生在高考中不能順利完成問題求解,究其原因,其實是沒有真正理解這類問題的數學實質,如果教師在教學過程中也能對所做的題目進行一些類似的變形和拓展研究,相信一定能更深刻地理解數學.因此,認真探究這類題的不同解法以及拓展是很有必要的.

4.2 理解學生,突破難點

高中數學課程面向全體學生,要以學生發展為本,立德樹人,提升素質,實現人人都能獲得良好的數學教育,不同的人在數學上得到不同的發展.不同學生可以選擇不同的解題方法,本題中探究1起點低,容易入手,難點是運算,若運算能力不強,可研究探究2和探究3.事實上,從筆者所教的學生高考情況來看,由于學生基礎差別很大,同樣的講解,得分差別卻非常大,可見,理解學生,實際上是要了解他們的需求,根據不同基礎的學生提供不同的指導方案.當然,探究2也不是無本之木,如2015年北京卷文科第20題.

題目 已知橢圓C:x2＋3y2＝3,過點D(1,0)且不過點E(2,1)的直線與橢圓C交于A,B兩點,直線AE與直線x＝3交于點M.

(1)求橢圓C的離心率;

(2)若AB垂直于x軸,求直線BM的斜率;

(3)試判斷直線BM與直線DE的位置關系,并說明理由.

分析 第(3)問要證DE//BM,如圖3所示,可利用幾何性質

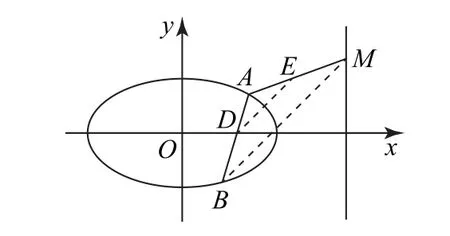
圖3

類似于探究2.

4.3 理解教學,使學生會思考

數學教學的本質就是在教師的幫助下,學生通過學習,揭示數學規律,總結數學方法,形成良好的數學思維的過程.因此,教學是一種不斷變換角度的過程,只有不斷地調整教師的已有的觀點來適應不同學生,才能做到真正地理解教學.這道高考壓軸試題難度高,一般學生難以發現解題突破口,我們可以把它作為一個資源進行再開發,引導學生結合題目中圖形的幾何特征,理順曲線與直線之間的位置關系,理解運算對象,由易到難設計啟發性問題,讓學生主動探究,分析出合理的轉化方向,在運算的過程中積累數學運算經驗.如此,教師就能真正地理解數學教學,也能引導學生學會思考,從而構建真正意義上的理解教學.

(完)