不同參數對塔機吊重擺角和塔身結構振動的影響*

劉 富,楊建偉,2*,謝貽東

(1.北京建筑大學 機電與車輛工程學院,北京 100044;2.北京市建筑安全監測工程技術研究中心,北京 100044)

0 引 言

目前,有許多研究者在靜力載荷作用下對塔式起重機(簡稱塔機)進行了二維特性分析。但是在工程實際中,塔機通常是在耦合運動作用下進行工作的。

很多學者采用有限元方法研究了塔機在不同狀態下的結構振動特性。

YANG Zhi-jun等人[1]采用有限元方法對塔機進行了力學分析,并在4種工況下,研究了塔機的穩定性和強度特性;但是,該研究忽略了塔機的動態特性。邊曉偉等人[2]利用有限元軟件對塔機結構進行了靜態分析,在不同載荷共同作用下,得到了塔機的位移云圖,也對塔機強度和模態進行了分析;但是,該研究忽略了塔機運動對其強度和模態的影響。鄧勇等人[3]利用有限元軟件,研究了起重臂仰角大小對塔機抗震性能的影響;但是,該研究忽略了吊重擺角與塔身振動的相互影響。高崇仁等人[4]開發出了一種塔機多工況有限元分析求解器;但是,求解器忽略了吊重擺角的影響。USHIO Y等人[5]提出了一種新的超級計算機靜力彈塑性有限元分析方法,采用該方法對端板拉伸螺栓連接處進行了分析,能夠設計出精度高、可靠性強的螺栓接頭;但是其忽視了塔機動態運動對連接處的影響。KENAN H等人[6]建立了一種有限元模型,該模型能夠用于計算結構的固有頻率、質量參與因子和模態振型;但是,其沒有研究塔臂振動對塔身的影響。張大可等人[7]采用仿真方法,建立了變幅機構的剛體動力學模型,研究了不同參數對吊重擺角的影響;但是,其忽略了塔機結構的彈性影響。崔少杰等人[8]采用有限元方法,研究了靜力狀態的風載荷對塔機結構在工作和非工作狀態下的影響;但是,其沒有考慮動力學對塔機的影響。嚴飛等人[9]采用有限元方法,研究了材料非線性和幾何非線性對塔機靜態結構的影響;但是,其忽略了吊重擺動角度對塔身振動的影響。

在部分文獻中,作者采用解析解的方法,研究了塔機在靜動力狀態下擺動角度和塔臂振動特性。

HE Wei[10]建立了一種變速度的懸浮載荷系統的平面理論模型;但其忽略了初始角度對塔臂的影響。FENG Run-hui等人[11]建立了單一運動下有效載荷-小車-塔臂的系統動力學方程;但是,其未考慮耦合運動的影響。JIN Liang-hai等人[12]建立了柔性繩在風載作用下的擺動角度系統模型,研究了風荷載對塔機擺角的影響;但是,其忽略了塔身和塔臂振動的影響。蘭朋等人[13]采用彈性動力學理論,研究了塔機在回轉運動下動態特性;但是,其未考慮耦合運動的動態特性。于蘭峰等人[14]采用集中參數法,研究了塔機結構的動力學特性,其建立的模型最大自由度為4;但是,其未把初始角度作為輸入參數。董明曉等人[15-17]研究了吊重在變幅運動下的擺動規律,還研究了回轉運動對塔臂振動的影響,也研究了不同的吊重和變幅運動對塔臂振動特性的影響;但是,其未考慮塔機加速度對塔機結構的影響。

綜上所述,在靜力作用下、在單一運動下或者在動力作用下,針對塔機結構振動特性的研究已取得豐碩的成果。但是,上述很多文獻把塔機結構當作剛性結構來研究,大量文獻也未考慮塔機的加速度對吊重擺角的影響,針對塔機在提升與回轉耦合運動下結構振動和空間擺角特性研究的文獻則更少。

為了揭示塔機在該提升與回轉耦合運動下結構非線性振動的機理,需研究塔身結構非線性振動和吊重的空間擺動在耦合運動下的規律。

因此,針對塔機在提升與回轉耦合運動下的結構非線性振動,筆者通過建立塔機從加速到恒速再到減速的動力學模型,研究不同參數對塔身結構非線性振動和吊重擺角的影響。

1 塔機動力學模型

目前,塔機在土木工程領域的應用廣泛。塔機的耦合運動在實際工程中比較常見,提升與回轉耦合運動對塔機結構非線性振動和吊重擺角的影響比較大。但是為了減少計算量,在工程設計時,一般會將動力問題(采用較大的安全系數)轉化為靜力問題。該方式會造成結果的不準確。

因此,筆者從動力學角度出發,對塔機在提升與回轉耦合運動下的非線性振動進行研究。

1.1 塔機位移關系

隨著塔機提升運動的進行,繩長Ly在運動過程中不斷變化。各相鄰質量之間通過無質量單元連接,各單元存在一定的剛度和阻尼。

非線性運動的塔機結構如圖1所示。

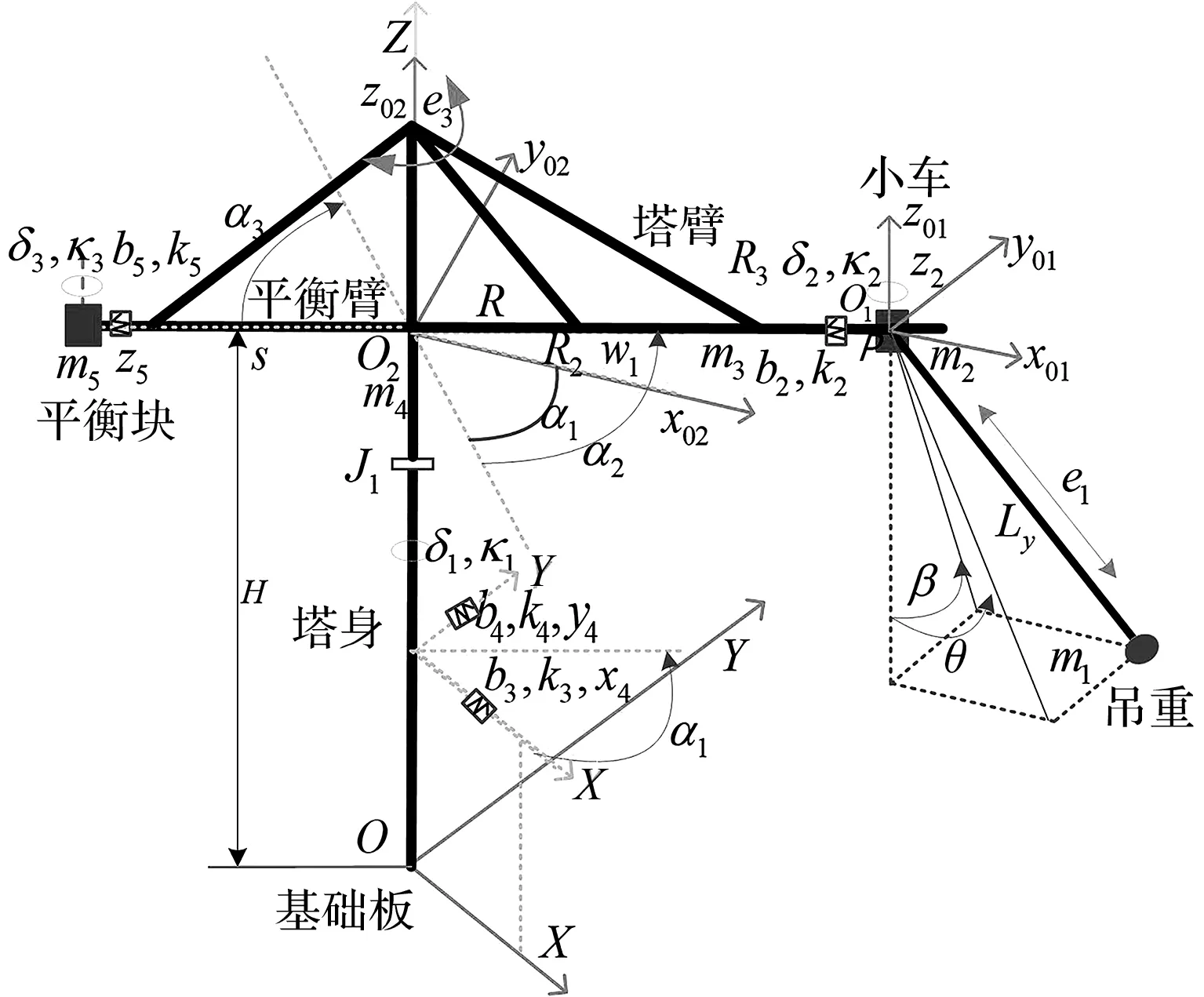
圖1 塔機模型示意圖

根據塔機系統相對坐標和廣義坐標之間的關系,可得廣義位移與結構參數關系如下:

(1)

隨著塔機從加速到恒速再到減速運行,繩長Ly、角度δ4和角度δ5不斷改變。

塔機的減速度和加速度絕對值相等,繩長、平衡臂旋轉角度、塔臂旋轉角度與時間關系為:

δ5=δ4+π+δ3-δ2

(2)

(3)

(4)

式中:t1為塔機的加速運行結束時刻;t2為恒速運行結束時刻;t3為減速運行結束時刻;L為初始繩長;r為回轉齒輪嚙合線半徑。

假設塔臂為懸臂梁,根據梁撓度理論及受力分析結果,可求出塔臂撓度如下:

(5)

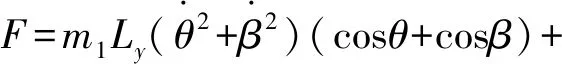
(6)

式中:F為吊重施加在塔臂上的力;E為塔臂的彈性模量;I為塔臂的慣性矩。

1.2 拉格朗日動力學建模

塔機的廣義速度、總動能以及總勢能分別為:

(7)

(8)

(9)

式中:Xp為質量p在X軸方向上的位移;Yp為質量p在Y軸方向上的位移;Zp為質量p在Z軸方向上的位移;vp為質量p的合速度;αp為質量p扭轉角;T為總動能;V為總勢能;sp為單元p彈性的伸長量;γp為質量p角度的旋轉量;hp為質量p的高度。

根據塔機的幾何關系,可推出吊重擺長與擺角的關系如下:

x1=Lysinθ

(10)

y1=Lysinβ

(11)

各個單元的阻尼力和空氣阻力為:

(12)

(13)

式中:Qr,pi為質量p的廣義坐標i的空氣阻力;Qd,i為廣義坐標i的阻尼力;c為空氣阻力系數;ρp為空氣密度;Sp為迎風面積;qi為廣義坐標;di為阻尼系數。

基于受力分析,可知廣義非保守力如下:

Qi=Qr,pi+Qd,i

(14)

引入拉格朗日動力學表達式如下:

(15)

式中:t為塔機的運行時間;Qi為廣義坐標i的非保守廣義力。

將式(1)～式(14)代入式(15)中,可推導出結構非線性振動映射關系如下:

(16)

2 實驗測試與驗證

根據實際塔機結構,筆者首先設計了塔機實驗模型結構參數,確定了塔機的材料(Q235);接著選擇了角度傳感器和采集儀,設計了HWT905傳感器布置點,根據設計的尺寸加工了塔機裝備,進而安裝了實驗裝備;然后,布置了吊重擺角傳感器和連接采集儀,調試了實驗塔機和采集儀;最后,進行了實驗測試。

2.1 實驗步驟與參數

實驗人員操作塔機,使其進行提升與回轉耦合運動,并進行擺角數據采集。每次塔機運行都是從加速到恒速再到減速。在實驗測試時,筆者選擇3個不同的吊重進行實驗,每個條件下重復3次,最后取平均值。

筆者設計的實驗塔機結構參數值如表1所示。

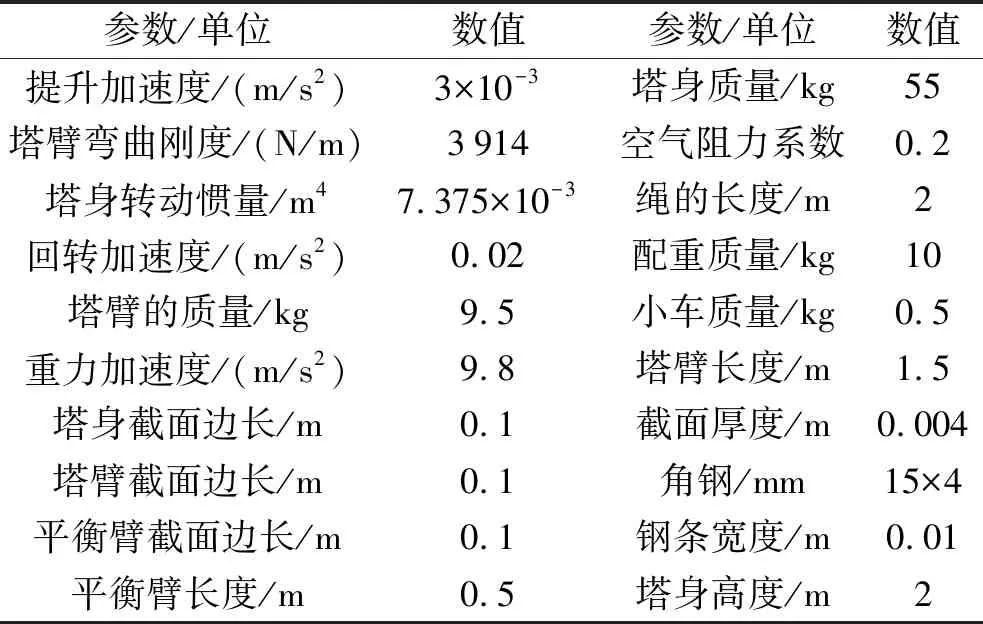
表1 塔機設備結構參數

測試設備布置如圖2所示。

圖2 實驗的設備

2.2 實驗與仿真結果對比

實驗結果與仿真結果的對比情況,如圖3所示。

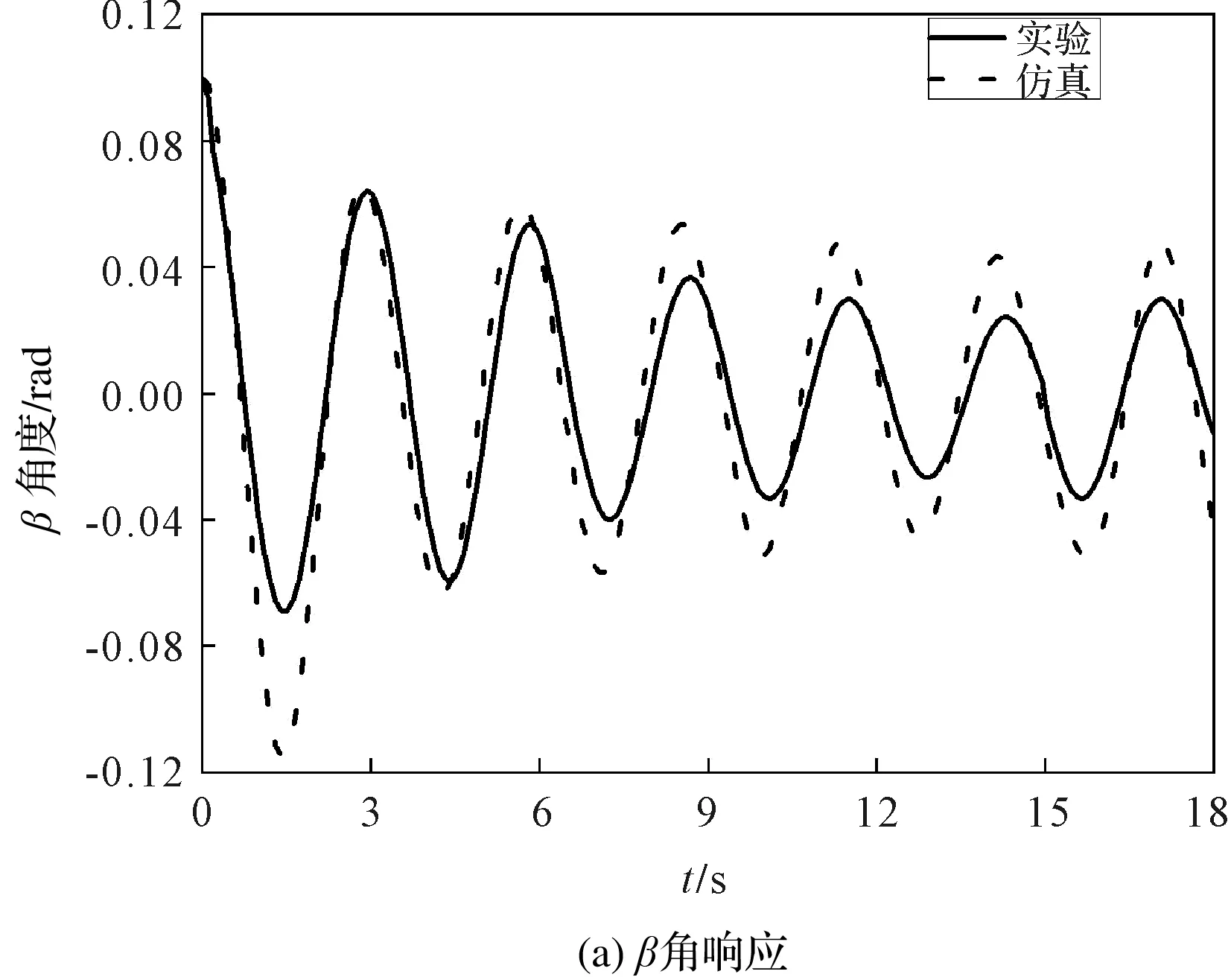
圖3 實驗結果與仿真結果對比

從圖3可以看出:在加速和減速階段,仿真結果與實驗結果有一定的差距,兩者在恒速階段差距比較小,仿真與實驗的結果整體變化趨勢一致。

因此,上述非線性塔機模型能呈現塔機真實的振動特性。

3 非線性動態響應和分析

基于已建立的塔機動力學模型,筆者研究不同參數對塔機吊重擺角和塔身振動的影響。

3.1 不同參數對吊重擺角振動的影響

3.1.1 改變提升加速度

改變提升加速度對吊重擺角的影響如圖4所示。

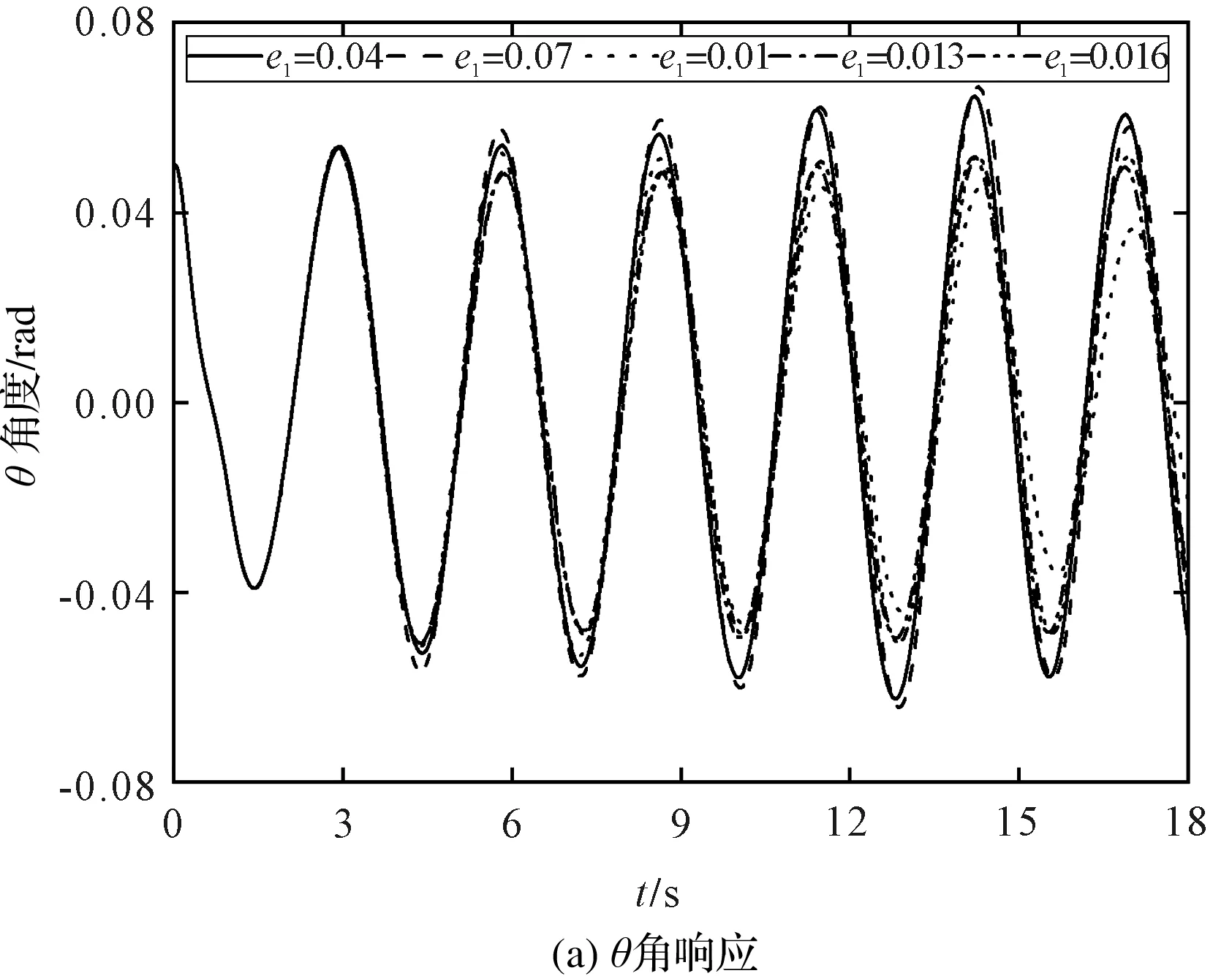
圖4 不同提升加速度對吊重擺角的影響

從圖4(a)可以看出:隨著時間的增加,角θ先增加后減小。在恒速末期時,擺角θ存在最大值;在加速度階段,擺角θ變化不明顯。當提升加速度為0.01 m/s2時,擺角θ存在最小值;當提升加速度不大于0.007 m/s2時,擺角θ較大。

從圖4(b)可以看出:擺角β在減速階段存在最大值。隨著提升加速度的增加,當提升加速度為0.007 m/s2時,擺角β存在最大值。提升加速度在塔機加速運行階段對擺角β無明顯影響;在恒速和減速階段對擺角β有一定影響。

由此可見,提升加速度對θ角的影響比β角大。

3.1.2 改變回轉加速度

改變回轉加速度對吊重擺角的影響如圖5所示。

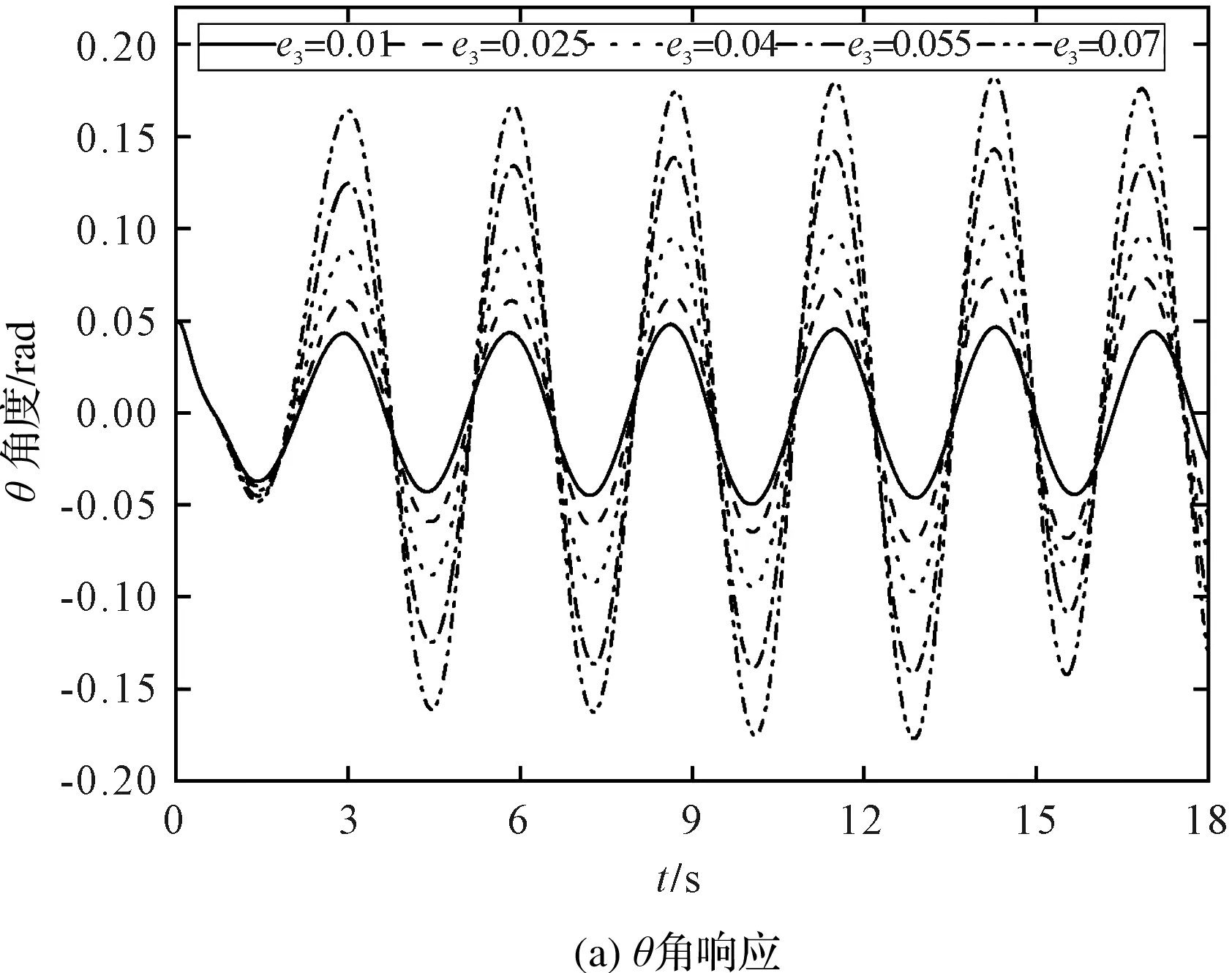
圖5 不同回轉加速度對吊重擺角的影響

從圖5(a)可以看出:在恒速階段,隨著時間的增加,角θ的振幅有最大值;在加速階段,振幅有最小值。隨著回轉加速度的增加,角θ的振幅逐漸增大,角θ的振動周期幾乎不變。

從圖5(b)可以看出:隨著回轉加速度的增加,角β的振動周期逐漸減小。當回轉加速度為0.07 m/s2時,擺角β存在最大值。

因此,回轉加速度對角θ的振幅影響比角β的振幅大。

3.1.3 改變β0角

改變β0角對吊重擺角的影響如圖6所示。

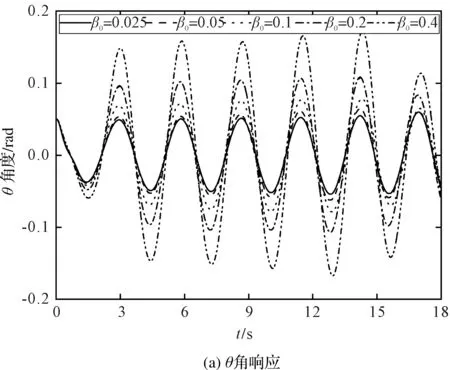
圖6 不同β0對吊重擺角的影響

從圖6(a)可以看出:隨著初始角度β0的增加,角θ的振幅不斷增大,但是振動周期不變。隨著時間的增加,不同的角β0在加速和恒速階段對角θ的振幅差距存在不同程度的影響;在減速階段,對角θ的振幅差距影響變小。

從圖6(b)可以看出:隨著初始角度β0的增加,角β的振幅明顯增大,但是振動周期沒有顯著變化。在加速和恒速階段,隨著時間增加,不同的角β0對角β的振幅差距存在一定程度的影響。初始角度β0對空間擺角的振幅存在較大的影響。

因此,初始角度β0對角β的振幅影響比角θ的振幅大。

改變θ0角對吊重擺角的影響如圖7所示。

圖7 不同θ0對吊重擺角的影響

從圖7(a)可以看出:隨著初始角度θ0的增加,角θ的振幅顯著增加,但是振動周期沒有明顯變化。在恒速末期時,角θ的振幅存在最大值。隨著時間的增加,改變的初始角度θ0對角θ振幅的差距影響比較穩定。

從圖7(b)可以看出:隨著初始角度θ0的增加,角β振動周期逐漸減小。當初始角度θ0不大于0.4 rad時,隨著角度θ0增加,角β的振幅逐漸減小。當角θ0為0.4 rad時,角β的振幅明顯增大;振幅在恒速階段有發散趨勢。

由此可見,初始角度θ0對角θ的振幅影響比角β的振幅大。

3.2 不同參數對塔身結構振動的影響

通過對塔機動力學模型的分析,筆者發現不同的提升加速度對塔身結構振動的影響很小。

3.2.1 改變回轉加速度

改變回轉加速度對塔身振動的影響如圖8所示。

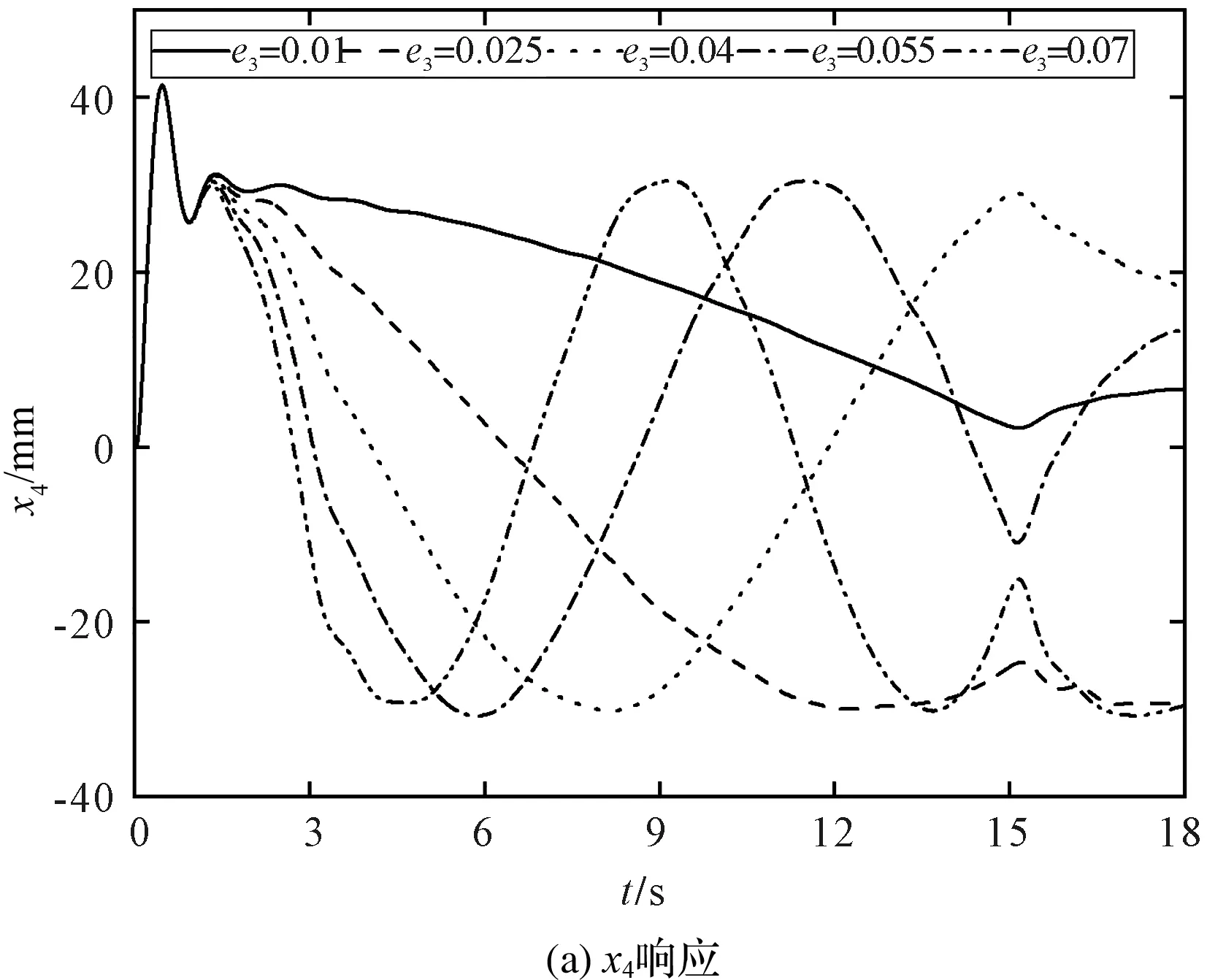
圖8 不同回轉加速度對塔身振動的影響

從圖8(a)可以看出:隨著回轉加速度的增加,塔身振動周期在x軸方向上逐漸減小;塔身振幅在加速階段存在最大值;

從圖8(b)可以看出:隨著回轉加速度的增加,塔身振動周期在y軸方向上逐漸減小。當回轉加速度為0.07 m/s2時,塔身的振幅在y軸方向上有最大值。當回轉加速度不大于0.01 m/s2時,塔身的振幅沿x軸和y軸方向較小。

因此,回轉加速度在恒速和減速階段對塔身振動影響較大。

3.2.2 改變β0角

改變β0角對塔身振動的影響如圖9所示。

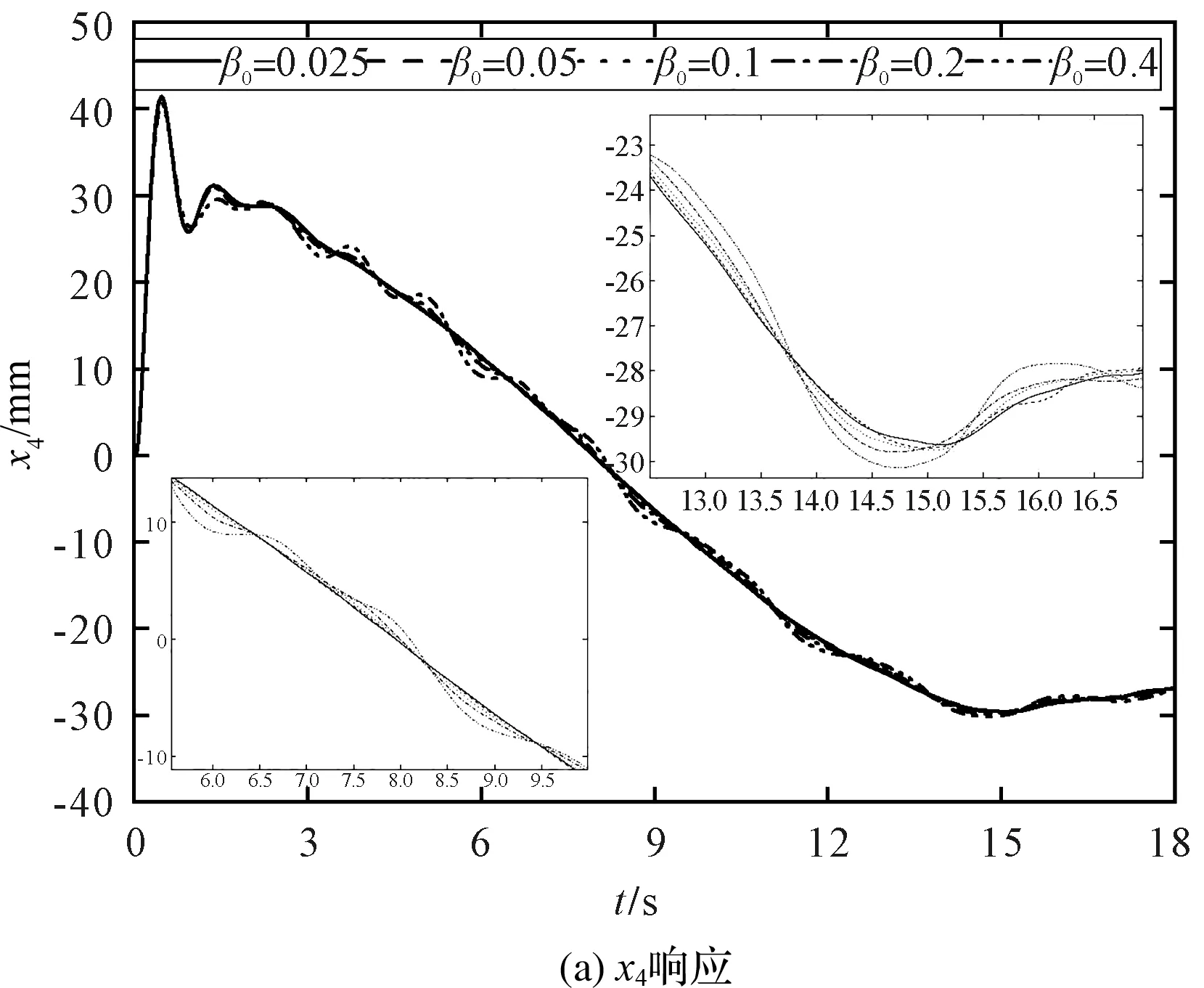
圖9 不同β0對塔身振動的影響

從圖9(a)可以看出:隨著初始角度β0的增加,塔身x4在減速與恒速階段周期和幅值均增加。當初始角度β0不小于0.4 rad時,塔身振幅在加速階段沿x軸方向減小。

從圖9(b)可以看出:隨著初始角度β0的增加,塔身振幅沿y軸方向增加;沿y軸方向在恒速階段比在加速和減速階段增加量大。當初始角度β0不小于0.2 rad時,塔身振幅在加速和恒速階段沿y軸方向波動較大。

因此,初始角度β0在y軸方向上的影響比在x軸方向上大。

3.2.3 改變θ0角

改變θ0角對塔身振動的影響如圖10所示。

圖10 不同θ0對塔身振動的影響

從圖10(a)可以看出:隨著初始角度θ0的增加,塔身的振幅和周期沿x軸方向增大。當θ0角不小于0.2 rad時,塔身x4的振幅在加速階段增加不顯著;x4的振幅在恒速和減速階段波動較大;

從圖10(b)可以看出:隨著初始角度θ0的增加,塔身的振幅和周期沿y軸方向增大。當θ0角不小于0.2 rad時,塔身y4的振幅在加速階段變化不明顯;y4的振幅在恒速和減速階段波動較大。

因此,初始角度θ0在x軸方向上的影響比在y軸方向上大。

4 結束語

針對塔身振動和吊重擺角在提升與回轉耦合運動下的變化規律進行了研究,筆者進一步研究了塔機從加速到恒速再到減速的運行規律。通過改變提升加速度、回轉加速度和初始角度的數值,對塔機結構非線性振動進行了研究;探討了不同參數對塔身結構振動和吊重擺角的影響。

研究結論如下:

1)提升加速度對角θ振幅的影響比角β振幅大;選擇較大的提升加速度對擺角和塔身振動影響較小;

2)回轉加速度對吊重擺角振動周期和幅值的影響較大。回轉加速度對角θ振幅的影響比角β振幅較大;選擇合適的回轉加速度能減小擺角振幅和周期;

3)回轉加速度對塔身結構振動周期和幅值的影響較大。選擇較小的回轉加速度能降低塔身結構振幅;

4)初始角度對吊重擺角的振幅有明顯影響。當改變初始角度的方向與吊重擺角方向一致時,吊重擺角在該方向上受到較大影響;

5)當初始角度小于0.2 rad時,初始角度對塔身結構振動影響較小。

在后續的工作中,筆者將從疲勞角度出發,研究不同的結構參數對塔機關鍵位置的疲勞累積影響。