旋啟式止回閥關閉過程瞬態流固耦合特性研究*

趙 帥,盛麗媛,陸 程,朱榮生,陳一鳴,付 強*

(1.江蘇大學 國家水泵及系統工程技術研究中心,江蘇 鎮江 212013;2.中國核電工程有限公司,北京 100840;3.核電泵及裝置智能診斷運維聯合實驗室,江蘇 鎮江 212013)

0 引 言

在各種流體管路系統的水力過渡過程中,經常會出現水錘現象。兩階段止回閥作為一種防護效果相對較好的水錘防護設備,其具有安裝使用簡單、占地面積小等的優點[1-3],因而被廣泛應用于各類大型泵站以及給排水系統中。

重要廠用水系統承擔了核電廠最終熱阱的功能,設有旋啟式的兩階段止回閥。

眾多學者對兩階段止回閥的最佳關閉時間進行了深入的研究。楊嘉等人[4]針對某一核電廠的重要廠用水系統,利用AFT計算軟件,對其水錘特性進行了詳細的研究,并得到了核電廠系統的最佳關閥時間。毛雨佳等人[5]對比分析了某工程實際的不同止回閥關閉方案下的液柱分離、機組倒流百分比等問題,分析得到了推薦選擇快關4 s、緩關7 s的關閉方案。

眾多學者對止回閥的工程應用及關閉規律進行了研究,但其流動特性以及結構響應的相關研究仍然相對薄弱,有待于深入。止回閥作為一種水錘防護流體機械(設備),研究其流固耦合特性,不僅利于設備的維護和優化設計,還對核電廠的安全穩定運行具有重要意義。

采用試驗研究止回閥的流固耦合特性,雖然能夠獲得更為準確的結果,但往往很難取得可視化的閥門內流場變化特性。此外,針對流場作用導致的應力應變測量難度較高,需要巨大的周期與資源投入。因此,目前普遍采用的研究方法是,用Fluent動網格技術來模擬閥板、閥芯的運動,以進行計算流體動力學(compu-tational fluid dynamics,CFD)仿真[6-7]。

動網格技術目前已較為廣泛地應用于各種具有動部件設備的仿真研究中[8-12]。它不僅在閥門的仿真中展現出了較好的效果,還使仿真結果和閥門試驗實現了很好的對應[13]。

近年來,基于動網格技術方法,許多學者已對各種形式的止回閥開展了流固耦合特性的研究。

段峰波等人[14]采用流固耦合的方式,對軸流式止回閥的開啟過程進行了仿真,獲得了止回閥流速與應力之間的變化規律。鄒亮等人[15]利用動網格的方法,對不同彈簧剛度下的單向閥關閉過程進行了二維仿真,并進行了對比分析,可為合理選擇單向閥的彈簧剛度提供參考。浦承皓等人[16]對核安全級旋啟式止回閥進行了單向流固耦合仿真,仿真結果可為閥瓣的設計提供參考。

這些研究都證實了該方法的優勢與可行性。

綜上所述,針對某核電廠重要廠用水系統止回閥內部流動特性缺失應力應變分析、試驗研究較難等問題,筆者采用動網格方法,建立流固耦合計算模型,并進行仿真計算,以深入了解止回閥的流固耦合特性,為止回閥的后續優化設計提供參考[17-20]。

1 數值計算模型

1.1 閥門幾何模型

旋啟式止回閥模型如圖1所示。

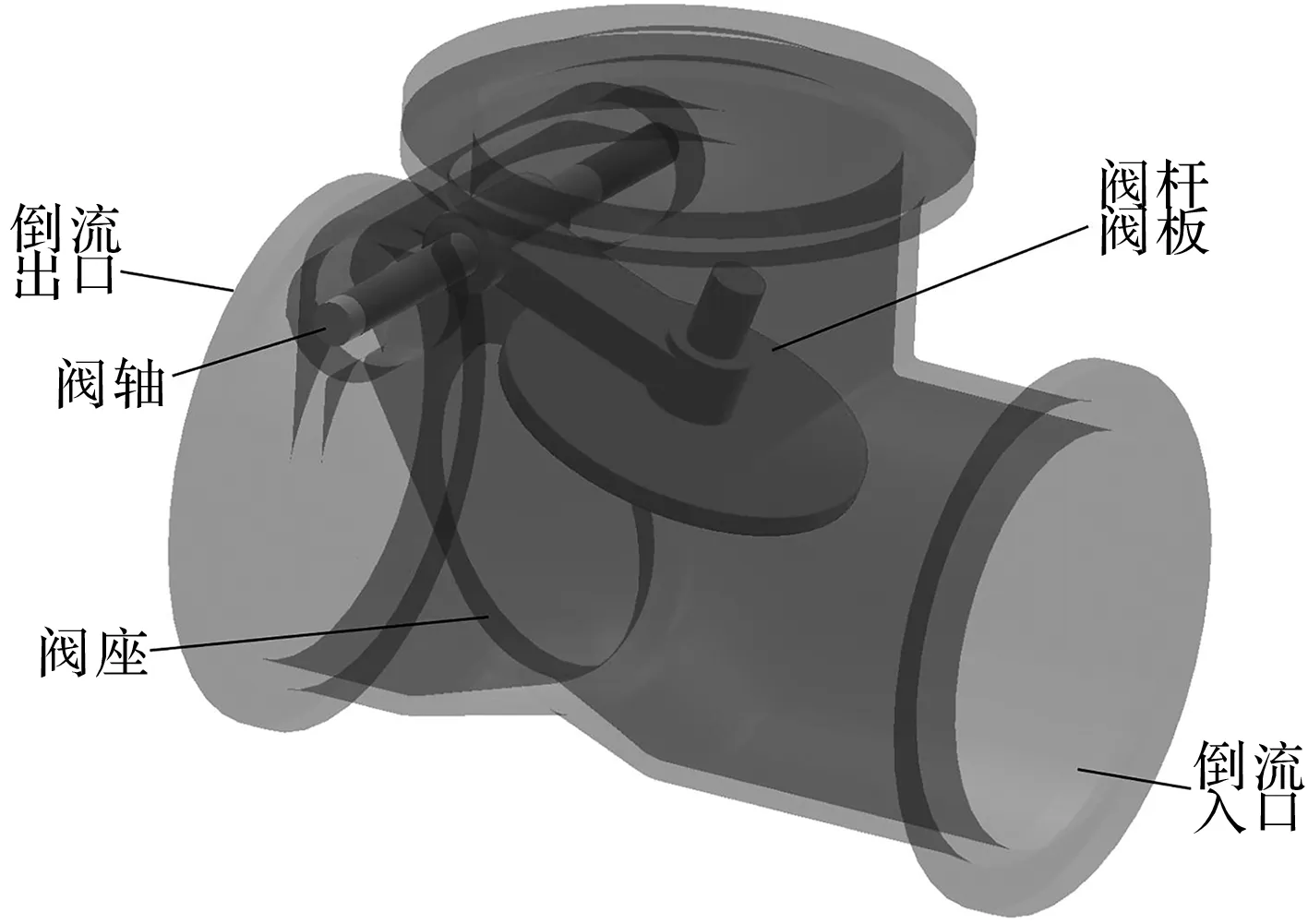
圖1 旋啟式止回閥模型

圖1為止回閥的三維模型(其原始圖紙由電廠提供)。

在止回閥運行時,海水由重要廠用泵輸送,通過止回閥入口進入閥內流道。在4 s時間內,閥門需實現全開。停泵工況下,流體由于系統高度差發生倒流,此時止回閥開始關閉;采用外部裝置控制閥門的關閉速度。

在模擬過程中,需同時考慮流道內的流體和閥門部件的響應,因此,筆者利用圖1中的固體部分進行水體區域的抽取,以進行CFD仿真模擬與分析。

為保證流體的流動得到充分發展,筆者在流體域上下游設置長度為8 m的進出口延長段。

1.2 網格劃分

筆者采用Fluent mesh對水體區域進行非結構化網格的劃分。

為保證閥門模型與實際情況相似,筆者采用靜態仿真方法,對止回閥的流量系數進行計算。

對模型進行多次修改后的結果表明:模型的流量系數為39 960,與實際的38 800相比,誤差為2.99%。

為排除網格數量對計算結果造成的影響,筆者對其進行網格無關性驗證,其結果如圖2所示。

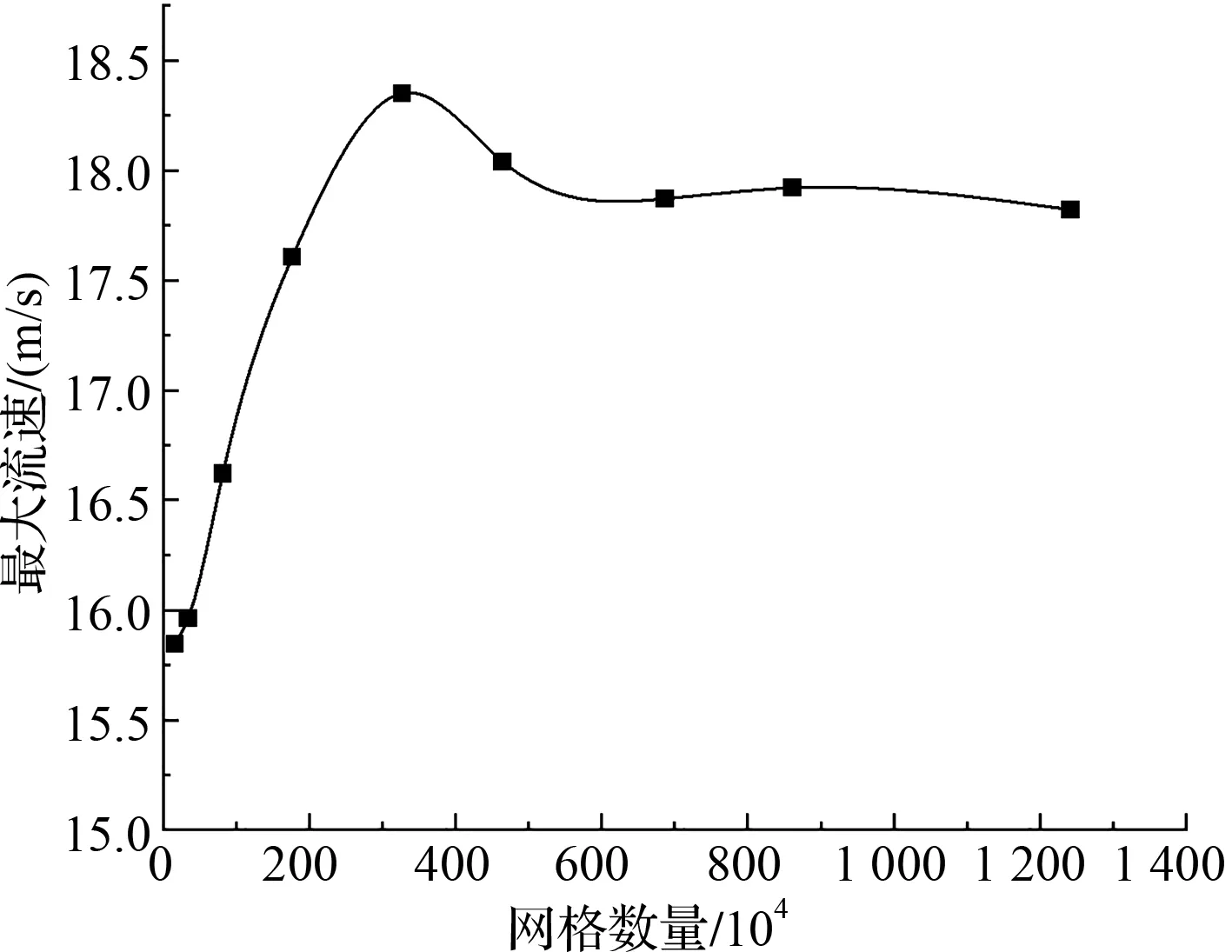
圖2 網格無關性驗證

由圖2可知:當網格數較少時,由于對于流動細節的捕捉不夠,其計算結果偏小;當網格數達到6×106以后,計算結果逐漸趨于穩定。

筆者綜合考慮計算時間與結果偏差,得到流體計算域和固體計算域的網格,如圖3所示。

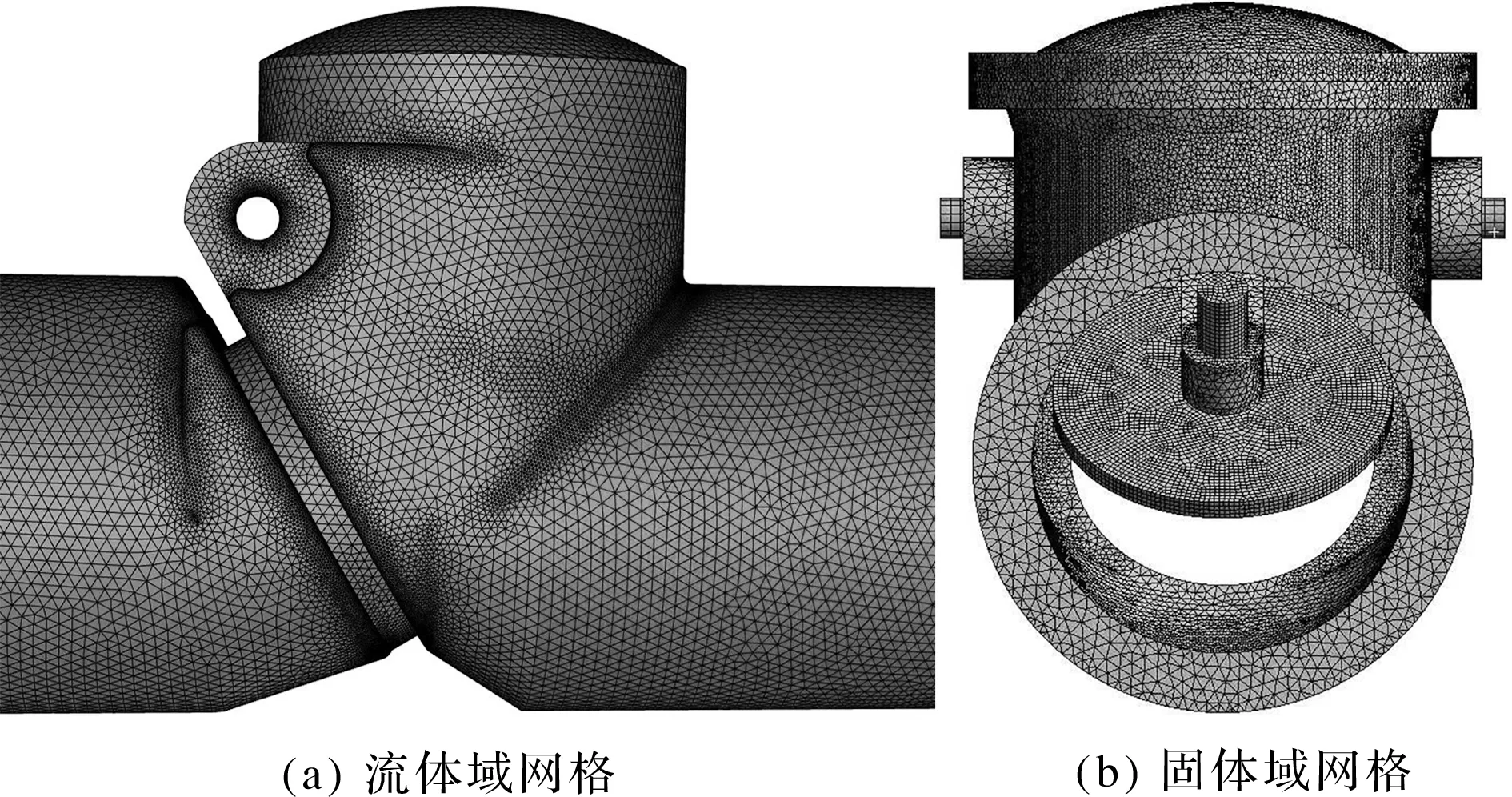
圖3 流體域及固體域網格劃分

水體區域網格單元數共6 868 060,網格質量在0.37以上。筆者在CFD軟件的Fluent中,對流體域進行求解,并在ANSYS Workbench中,進行閥門固體部分的網格劃分和有限元求解。

閥門固體部分的網格采用四面體網格,整個閥體域被劃分為2 752 038個網格單元。

止回閥閥體主體材質為碳鋼20MN5M,閥板和閥軸采用SAF2507雙相不銹鋼[21]。

止回閥材料性能參數如表1所示[22]。

表1 止回閥材料性能

1.3 動網格算法

在閥門的啟閉過程中,隨著閥板的旋轉,閥內流場時刻發生變化,且閥板外沿具有較大的位移,因此,筆者采用動網格的方式對其進行仿真模擬[23]。動網格方法是在選擇擴散光順的同時,打開網格重構選項。

網格運動區域包括閥板及閥桿部分,筆者將其定義為剛體,并設置其繞閥軸軸心旋轉。彈性光順在三維模擬中適用于四面體網格;局部重構法適用于大變形或者大位移情況。當網格扭曲過于嚴重、網格尺寸過小或過大時,網格會自動在設定范圍內進行局部重構,以滿足扭曲和尺寸的要求[24]。

為保證計算的收斂性,除設置最大、最小網格重構尺寸外,筆者將網格重構間隔修改為1,以保證閥板運動后的空缺及時有新網格進行補充。

研究人員一般采用profile或udf功能控制動網格。此處,筆者采用profile功能控制閥板運動。相比于udf功能,profile僅需在控制文件中設置對應不同時刻的控制條件,不需要編寫程序,更容易使用。

根據核電廠的相關瞬態計算,止回閥具有較好防護效果的關閉方式(這也在實際電廠中得到了應用)為:第一階段,在4 s內,由最大開度40°關閉90%至4°;第二階段,在12 s內,實現全關,即開度為0°。

因此,根據工程實際可得到止回閥開度隨時間的對應關系,如圖4所示。

圖4 止回閥開度隨時間變化關系圖

根據閥板開度和關閉的時間,筆者計算并設定閥板轉動角速度。其關閉過程第一、二階段旋轉速度分別為π/20 rad/s、π/540 rad/s。

1.4 流體計算條件設置

由于止回閥內的工作介質為海水,筆者采用瞬態數值模擬方法,借助標準k-ε湍流模型封閉流動控制方程,并使用SIMPLEC算法,求解其流動控制方程。

在止回閥的關閉過程中,流體動力源為重力下的壓差。因此,筆者對計算域設置壓力入口和壓力出口邊界條件。其中,閥門入口壓力初始值設為88 000 Pa,出口壓力設為0 Pa。

1.5 流固耦合原理及計算設置

流固耦合分析是專門研究流體與可變形固體之間相互作用的一種分析方法。采用該方法可以獲得流體的速度壓力變化,以及流場作用下的結構響應[25-26]。

在進行流固耦合數值模擬時,需要遵循流體控制方程、固體控制方程以及耦合控制方程[27-28]。

其中,流體控制方程如下:

(1)

式中:ρ為流體密度;u,v,w為流體介質速度矢量在x、y、z方向的分量。

固體控制方程如下:

(2)

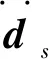
流場與固體場的耦合,主要表現在二者的位移、熱流量、應力守恒等方面,即:

df=ds

(3)

Tf=Ts

(4)

Qf=Qs

(5)

nf·τf=ns·τs

(6)

式中:下標f為流體;下標s為固體;d為位移;T為溫度;Q為熱流量;τ為應力。

流固耦合一般分為兩類,即單向流固耦合和雙向流固耦合。其中,單向流固耦合僅將流場計算結果導入固體域,不考慮結構形變造成的反作用。相對而言,雙向流固耦合具有更高的精度,但需要較大的運算資源。

綜合考慮計算時間,以及在工作場景下研究對象的變形程度對流場的影響,筆者選擇了單向流固耦合這一方法。

筆者借助ANSYS Workbench中的結構靜力學模塊,進行流固耦合分析,將采用Fluent得到的壓力載荷導入至交界面上[29]。

其中,交界面主要包括閥板、閥桿組合體,及閥體上蓋組合體這兩部分,如圖5所示。

圖5 閥體及閥板壓力載荷分布示意圖

由于閥門的出入口通過法蘭與管道系統連接,筆者認為閥門的入口與出口不發生位移,因而對其施加固定約束。

2 閥門內部瞬態流動分析

2.1 閥內流速變化

旋啟式兩階段止回閥關閉過程中,不同開度條件下的速度分布云圖如圖6所示。

圖6 止回閥關閉過程100%～5%開度下速度云圖

圖6(a)中,當閥門處于全開狀態時,閥板對介質的阻礙作用有限,介質倒流速度較大,達到了17.87 m/s,閥內流體大部分經閥板下側空間流入系統的上游,小部分流體沿閥板上側流入閥門的上部腔體,并撞擊閥壁,然后形成漩渦,其最終的流向為靠近閥座位置的空隙;由于閥板的阻礙作用,貼近閥板的底側區域以及閥座的左側區域流體較少,流速也較低。閥門上部腔體的位置距離主流動通道較遠,流速也較小。由于閥座產生的節流作用,致使流體受到剪切,并在相應位置形成高流速區域,止回閥的高流速區域主要位于閥座通道的左側。

圖6(b)中,隨開度的減小,高流速區域逐漸削弱,且其方向也出現由左下-中心的過程。此時,閥板關閉至一定程度,閥板的阻礙作用使得流體在流經閥座前具有一個向左上方的初始流動趨勢。因此,經過閥座后,其流動仍沿著閥體中心。

圖6(c)中,當閥門開度由24°關閉至8°時,高流速區域進一步減小削弱,但整體的分布未產生較大變化。

圖6(d)中,當閥門關閉至末期后,因閥板、閥座的阻礙,流體沿閥板面流動,最終在板面中心位置發生碰撞,并依靠壁面反彈,形成了此時的主要流動區域,即高流速區域的最后階段。此時,隨著閥板的旋轉閉合,閥門流量減小,因此,入口流速降低,閥門內部的最大流速也相應降低。當閥門關閉程度達到1°時,閥內的最大流速降至14.28 m/s。

2.2 閥內壓力變化

兩階段旋啟式止回閥關閉過程中的壓力分布云圖,如圖7所示。

圖7 止回閥100%～5%開度下壓力云圖

圖7(a)中,在關閉初期,閥門內存在較多壓力梯度層次。以閥板為分界線,右側的壓力基本在88 000 Pa左右,這是由于閥板之前只有管道設備,流體的流動和壓力未受到干擾與削弱。而在閥板分界線的下側,由于流動面積的減小,流速得到了提高,相應的壓力依據伯努利方程,下降了約30 000 Pa;隨著流體的繼續流動,流速進一步提高,壓力也進一步降低(特別是閥座處,壓力迅速地降低了多個層次,并在速度云圖中的最大流速區域形成了部分負壓);但隨著閥座左側管道流通面積的逐漸增大,流速又開始降低,使得壓力有所回升。

圖7(b)中,隨著閥門的關閉,壓力梯度層數不斷減少,最大負壓情況有所改善。正壓部分覆蓋更廣的區域,但總體的分布大致與初期相似,這是由于在閥門關閉前期,閥內具有較大流速的流體較多,壓力的分布呈現出較多層次。

圖7(c)中,當閥門繼續關閉時,過流面積進一步減小。此時流體主要通過閥板邊緣區域流出。由于流體流動方向不同,又互相干涉,壓力分布形狀變得不規則,閥座中心的最低壓力區域被阻斷,分割為上下兩個部分。

圖7(d)中,當閥門接近完全關閉時,僅剩小部分流體流出,而這小部分流體的流動方向更傾向于緊貼閥板壁面。不同邊緣位置的流體方向各不相同,相互對立位置的流體相互碰撞,便形成了部分相對低速與高壓的區域(即閥板下部的深灰色位置)。

3 閥門結構響應特征

3.1 閥門應力變化

在開度為100%、60%、20%、5%時,兩階段旋啟式止回閥的等效應力分布情況,如圖8所示。

圖8 止回閥100%～5%開度下等效應力云圖

由圖8可知:兩階段止回閥的最大等效應力出現在閥軸與閥體的連接處,其次為閥桿部分,而閥壁部分的等效應力總體較小。即使是止回閥關閉末期,其最大應力也僅為9.04×106Pa,與閥板組合體相差近兩個數量級。這是由于閥門關閉過程中,閥板受到流體向左的沖擊作用力,因此所受壓力主要依靠閥桿傳導至閥軸處,特別是軸的連接部位,該部位承擔了主要的作用力;閥板前后存在較大壓差,使閥板有關閉的趨勢,進一步加大了閥軸處的等效應力。

兩階段旋啟式止回閥關閉過程中,不同開度最大等效應力變化情況,如圖9所示。

圖9 止回閥關閉過程中不同開度最大等效應力

由圖9可知:在關閉開始時,由于閥門開度較大,流體作用力得到充分釋放,此時閥門的最大等效應力最小,為8.08×107Pa。隨著閥板的關閉,閥板承受流體沖擊的面積增大,最大等效應力不斷增大,且呈現出線性的增長趨勢。當開度為2°時,最大等效應力增大至1.54×108Pa。

3.2 閥門變形量變化

兩階段旋啟式止回閥在開度100%、60%、20%、5%時的變形量分布情況如圖10所示。

圖10 止回閥100%～5%開度下變形量分布云圖

由圖10可知:在閥門關閉過程中,閥體的變形量與閥板組合體相比很小,在整個關閉過程中的最大變形量僅為0.022 mm。這主要是因為閥體上的應力小,且閥體壁厚大,整體承壓能力更強。

閥門最大變形量位置為閥板最底部,并沿閥板底部向閥軸方向逐漸減小,這是由兩方面原因決定的:1)考慮到閥門的結構原理,在兩階段止回閥關閉過程中,由于受到液壓阻尼器的作用,某一瞬間的閥板與閥體可以視作具有一定剛度的整體,閥板的固定完全依靠閥桿與轉軸,因此,越遠離具有約束作用的轉軸處,越具有變形的空間;2)考慮到流場的作用特征(見圖7),在閥板前后兩側存在著不同的壓力區域,壓差使得閥板受到流體的不平衡作用力,使變形程度加劇;而閥體部分則不存在此類作用。

兩階段旋啟式止回閥關閉過程中,最大變形量的變化曲線如圖11所示。

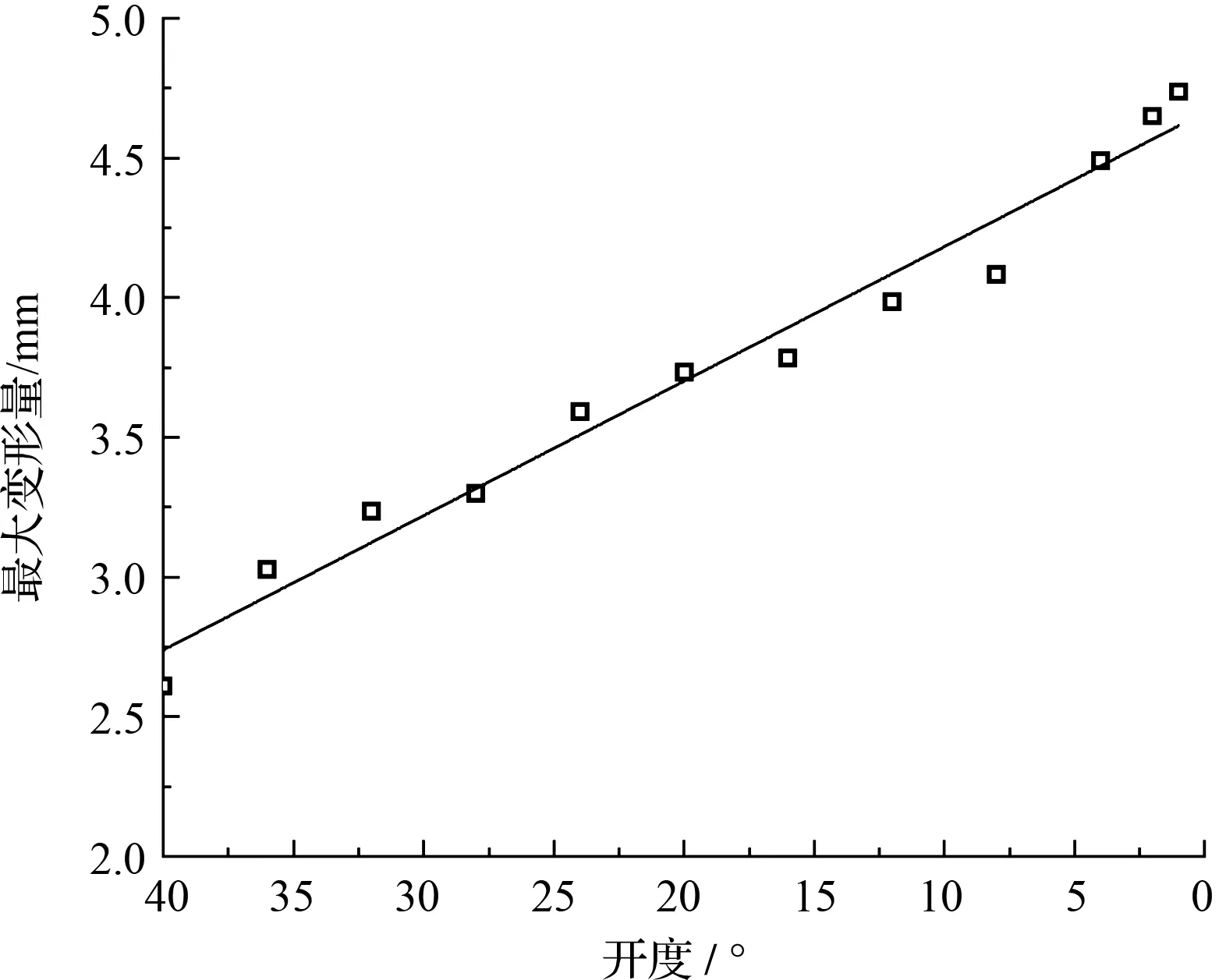
圖11 止回閥關閉過程中不同開度最大變形量

由圖11可知:在閥門關閉初期,最大變形量在整個關閉過程中最小,為2.6 mm,此時流體對閥板的沖擊并不大。

在關閉過程的第一階段,止回閥開度由40°關至4°,變形量迅速增加,當關閥的第一階段結束時,最大變形量為4.49 mm。

在第二階段的關閥過程中,關閉時間較長,但最大變形量仍在緩慢增長,直至完全關閉之前開度為2°時,其最大變形量已增至4.64 mm。這是由于隨著閥門開度的減小,閥板受到流體力的作用面積不斷增大所致(這與應力計算結果圖8、圖9相對應)。

4 結束語

針對某核電廠重要廠用水系統的兩階段旋啟式止回閥,筆者利用動網格方法,對其關閉過程進行了流固耦合仿真,并對其流速、壓力等流動特性以及應力、變形等結構響應進行了分析。

研究結論如下:

1)在閥門關閉初期,流通性好、流量大、流速高,此時高流速區域主要受到閥座影響;由于此時流速變化大,因此產生了較大的壓力變化。閥門關閉中期,流量有所減小,流速降低;此時,高流速區域受到閥板和閥座的共同作用,變得分散。閥門關閉末期,流速降至最低,流體沿閥板中心方向碰撞并反彈,高流速區域再次減少,并開始集中。整個過程中,閥內最大流速由17.87 m/s最終降至全關時的0 m/s;

2)在閥門關閉過程中,相對閥板組合體,閥體的等效應力較小,相差近2個數量級,其中最大等效應力出現在閥桿轉軸與閥體的連接處,為8.08×107Pa,并隨閥門開度的減小而增大至1.54×108Pa。相比于閥板組合體,閥體的最大變形量很小,相差近2個數量級,閥門最大變形量出現在閥板的最底部,為2.6 mm,且沿閥桿向轉軸方向逐漸減小,層次分明。隨著閥門關閉,最大變形量也逐漸增大,開度2°時的最大變形量已達到4.64 mm。閥門的最大等效應力、最大變形量與開度之間呈負相關。

根據以上得到的重要廠用水系統旋啟式止回閥關閉瞬態流固耦合特性,筆者后續可以針對流場能量損失較大的部位以及應力集中點進行優化設計,以提高設備的可靠性。

另外,在現有研究過程中,由于計算資源和時間有限,筆者采用的是單向流固耦合方法,計算結果可能還不夠準確。今后,可以采用雙向流固耦合的方式,對止回閥特性進行計算,以期得到更準確的計算結果。