分形理論在礦物加工中的應用基礎及研究進展

劉欣然 ，周偉光 ，謝廣元 ，彭耀麗，梁 龍，李懿江

(1.中國礦業大學 煤炭加工與高效潔凈利用教育部重點實驗室,江蘇 徐州 221116；2.中國礦業大學 化工學院,江蘇 徐州 221116)

礦產資源是國民經濟和社會發展的物質基礎，礦物加工技術是礦產資源高效提取利用的技術基礎。近年來，隨著礦產資源的開采、開發，我國礦產資源稟賦逐漸變差，礦物加工理論和工藝技術的升級與創新成為保障礦產資源綠色高效獲取的現實需求。鑒于此，學者們借鑒其他學科研究技術，通過多學科交叉、融合的方式開展研究，以期實現礦物加工過程環節優化及綜合指標提升。其中，分形理論因具有包容性強、運行方式靈活、應用范圍廣等特點，為礦物加工過程部分基礎問題的解決提供了良好的思路和借鑒。

分形理論是一門非線性學科，具有自相似性等基本特征，可用于描述自然界中各類非規則現象。發展之初，分形理論研究對象主要涉及河流道路軌跡及高分子鏈空間結構等，后逐漸應用于水處理領域，以表征懸濁液中絮體結構特性[1]。需要說明的是，礦物加工領域同樣涉及眾多非規則現象，分形理論的應用亦有助于解耦相關過程、闡明其機理。目前，礦物加工領域涉及分形理論的研究方向主要有：基于自然界礦石中有用礦物的分形分布規律，預測礦石機械揀選技術指標和經濟效益[2]；基于不同碎磨條件下礦石的粒度分形分布規律及形狀分形特征，優化工藝參數，研發新型破碎磨礦設備[3]；基于不同外界條件下礦漿懸濁液中絮體結構的分形特征，研究顆粒聚集/分散行為，提升浮選綜合指標，調控絮體沉降速率[4]；基于不同過濾條件下濾餅孔隙結構的分形特征，探索提高過濾效率的方法[5]等。

另一方面，與其他應用領域相比，分形理論在礦物加工中的應用仍處于發展階段，相關研究工作較少且不夠深入，大部分相關研究成果尚未投入實際生產。考慮到分形理論廣闊的潛在應用前景(尤其是選礦過程智能化和高效化發展方向)，有必要對前人研究成果進行總結、歸納，并在此基礎上理清、拓寬研究思路，明確未來研究方向。其中，在礦石揀選、礦石碎磨以及過濾(高濃度礦漿經過濾機加壓形成濾餅)過程中，分形研究對象為礦石碎塊、粒度較大的礦石顆粒以及含水量相對較低的濾餅，且各工藝環節通常處于干燥或礦漿濃度相對較高的環境中，一般不涉及微細礦物顆粒的混凝；在調漿、礦物浮選、沉降(包括過濾操作前礦漿懸濁液中礦物顆粒絮體沉降階段)過程中，分形研究對象為微細礦物顆粒及由微細礦物顆粒形成的絮體，且各工藝環節操作均處于液相環境中，涉及微細礦物顆粒的聚集/分散以及復雜混凝過程。因此，筆者將礦物加工過程中涉及分形現象的工藝環節分為“礦石揀選、碎磨及過濾”、“調漿-浮選與絮體沉降”2 部分，并分別對其中的分形現象進行分析，擬對分形理論在礦物加工領域的研究做出全面綜述。

筆者在概述分形理論相關概念基礎上，針對部分具有自相似性等分形特征的礦物加工工藝環節(包括礦石揀選、礦石碎磨、調漿、礦物浮選、沉降、過濾等)，歸納總結分形理論在以上工藝環節中的研究現狀，并基于各研究現狀分析、展望分形理論在礦物加工領域的發展方向，旨在基于多學科交叉以實現礦物加工學科的深入和可持續發展,為剖析某些復雜過程提供方法支持和技術借鑒。

1 分形理論

MANDELBROT 于1975 年提出了分形理論概念[1]，認為分形體具有自相似性(局部為整體的縮影)、無標度性及自放射性三大基本特征，這不僅表現在事物的圖形外觀上，還可體現在能量、時空、性質等方面。分形現象在自然界中普遍存在(圖1)，并廣泛應用于眾多學科的基礎研究。

圖1 常見分形現象Fig.1 Common fractal phenomena

歐氏幾何中維數僅能用整數表示，而對于復雜且不規則的分形體則需采用分形維數概念。分形維數是分形的度量指標，被用于描述分形體不規則程度及其在空間中的填充程度，可與諸多自然特性相關聯，具有極高的包容性。通常，二維分形維數適用于描述平面圖形幾何輪廓性質；三維分形維數能夠揭示分形體三維空間幾何特性；若顆粒群粒度分布具有分形特征，則可通過分布分形維數表征[3]。

依據研究對象特性差異，研究者提出了不同的分形維數定義方法，其中最常用的方法為相似維數。相似維數的本質是把研究對象看作一個可被劃分為N(F,r)個子集的集合F，每個子集以相似比r與原集合相似，如果存在一個數Df，使得當r→0 時有

則稱Df為研究對象的相似維數，即分形維數。該定義方法計算簡單、高效，廣泛適用于各類具有自相似性質的研究對象，但僅能對研究對象作整體性描述，無法精確描述其局部分維特性[1]。

分形維數計算過程模型如圖2 所示。礦物加工領域存在諸多分形現象，該模型能廣泛匹配各類分形現象的分形維數求解過程。例如，通過計算礦石中有用礦物分布分形維數，可揭示其中有用礦物分布規律[6]；通過計算碎磨過程中礦石粒度分布分形維數，可揭示不同碎磨條件下礦石粒度變化規律[7]；通過分析礦漿混凝過程中礦物顆粒絮體分形維數，可反映不同變量條件下絮體結構及顆粒動態變化規律等[8]。

圖2 分形維數計算過程模型Fig.2 Fractal dimension calculation process model

2 分形理論在礦石揀選、碎磨及過濾中的應用

2.1 分形理論在礦石揀選中的應用

現代礦石揀選過程通常利用傳感器，基于有用礦物與脈石礦物元素種類及含量等性質差異實現2 者的分離。揀選工藝主要包括礦塊揀選和礦石批量揀選2 種類型，其基本流程包括給料、傳感器檢測、信號處理以及物料分離4 個部分[9]。揀選工藝在礦石采選領域有廣闊的應用前景，但原有礦石批量揀選技術存在試樣礦物分布規律缺乏代表性、預期揀選技術指標與實際揀選效果差異大等缺陷，影響應用可行性。

自然成礦過程具有自相似性(圖3)[10]，礦石品位與質量存在分形關系(式(2))[6]，通常采用人工檢測的方法獲取礦石樣品的品位和質量數據，再通過分形維數定義計算礦物在礦石中的分布分形維數。

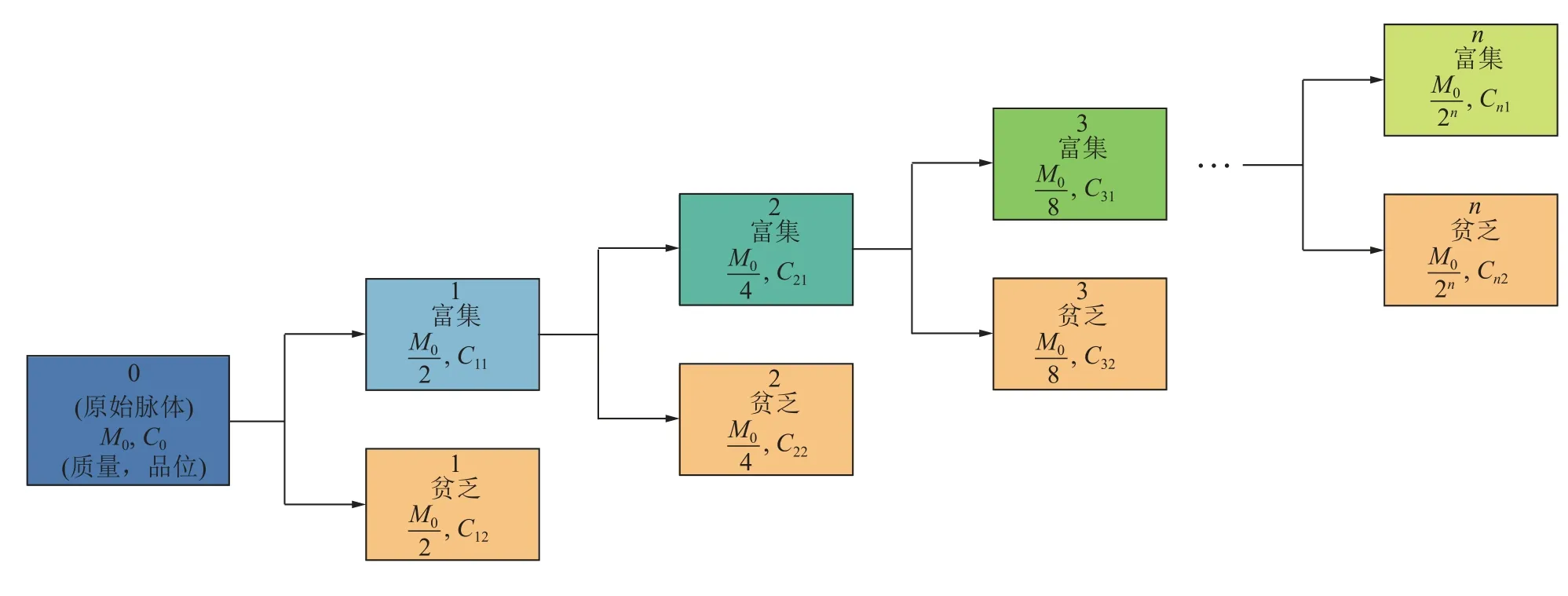
圖3 具有分形特征的成礦模型Fig.3 Metallogenic model with fractal characteristics

式中，C(M)為富集部分礦石品位；M為富集部分礦石質量；Dr為礦物在礦石中的分布分形維數，Dr越大，礦物分布越不均勻。

LI 等[2]發現將分形規律引入礦石批量揀選領域，并開展以下研究：首先，基于不同礦體中礦物分布規律的分形結構特性差異，在原有研究基礎上提出礦石批量揀選(BOS)模型(式(3))，并根據BOS 模型，建立礦石批量揀選技術指標(如給礦品位、精礦品位、精礦產率和金屬回收率)及經濟效益指標的預測模型。

式中，c為品位閾值；m為高于品位閾值累積礦石質量分數；G為分形量度，G越大，礦物越分布在較高品位下，可由對礦石樣品的品位和質量數據分析得到。

LI 等[11]以不同地區的3 種銅礦樣品為研究對象，對模型的準確性進行驗證，整體上準確度較高。總體而言，將分形理論引入礦石揀選過程建模中，可通過礦石性質有效預測揀選效果。雖然該研究仍停留在理論層面，尚未應用于實際生產，其后續深入研究卻對推動礦石批量揀選工業的快速發展大有裨益。

2.2 分形理論在礦石碎磨中的應用

礦石碎磨過程中，單一礦石的每次碎裂都將分裂成更小的礦石顆粒，礦石碎裂具有自相似性(圖4)[12]，因此該過程中礦石的粒度、形狀和能量消耗等性質變化均具有分形特征。

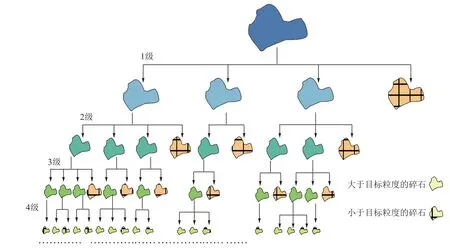
圖4 具有分形特征的礦石顆粒破碎模型Fig.4 Fractal model of ore particle crushing

2.2.1顆粒粒度分布分形規律

顆粒粒度是礦石碎磨過程中最重要的性能評價指標，其分布存在分形特征(式(4))[13]。通常采用粒度分布法研究礦石顆粒粒度分布分形維數，較為常見的粒度檢測方法有篩析法、沉降法和激光粒度測定法等：對于粒度較大的礦石顆粒，多采用篩析法；對于微細粒粉體，多采用激光粒度測定法。

其中，d為顆粒粒度；n為系統顆粒總數；Yn(d)為粒度小于d的顆粒數；Dg為粒度分布分形維數。Dg越大，細粒級所占比例越高，顆粒分布越不均勻，且顆粒表面越粗糙。當Dg接近2 時，礦石主要發生表面磨損；當Dg接近3 時，礦石主要發生整體碎裂[7]。

研究表明，礦石碎磨過程中顆粒粒度分布分形規律與碎磨工藝參數有著密切的關聯。例如，高鋒等[12]破碎磁鐵礦時發現，隨著破碎級數增加，礦石粒度分布分形維數逐漸增大，增大速率則逐漸減小并最終趨于穩定。ZHANG 和YANG 等[14-15]研究矸石和低階煤粉碎時發現，礦石粒度分布分形維數隨粉碎壓力(能量輸入)的增大呈先增大后趨于穩定的趨勢。楊志遠等[16]利用行星磨制備超細煤粉時發現，通過改變磨礦時間、添加助磨劑、優化球配比等調節顆粒粒度分布分形維數，能夠實現礦物磨礦過程及磨礦效率的有效控制。可見，基于顆粒粒度變化的分形特征研究，有助于實現對礦石碎磨工藝的過程優化與智能控制。

2.2.2顆粒形狀、碎磨能耗分形規律

礦石碎磨過程中，隨著顆粒不規則程度的增加，僅通過粒度分布評價礦石碎磨性能存在一定的局限性，于是研究者提出采用顆粒質量(三維)、投影面積(二維)、表面積分形維數描述顆粒特性。其中，質量分形維數采用質量-粒徑法計算(式(5))，投影面積、表面積分形維數則分別通過圖像分析法測量，即通過光學顯微鏡、透射電鏡或掃描電鏡拍攝顆粒圖像，隨后利用Image J 等圖像分析軟件測量顆粒投影面積和邊界長度，進而計算分形維數(式(6)、(7))[17]。

其中，M(d)為顆粒質量；A(L)為顆粒投影面積；L為投影特征長度；γ為碼尺長度；P(γ)為投影周長；Dm為質量分形維數；Da為面積分形維數；Dp為邊界分形維數。表面積分形維數Ds=Dp+1，Ds越大，顆粒表面越不光滑。

顆粒形狀分形維數不僅取決于碎磨工藝參數，還可與其他特征參數相聯系。焦紅蕾等[18]研究煤炭粉磨過程時發現，顆粒表面積和質量分形維數可用于磨礦能耗和產品成漿濃度的計算，并通過過程調控實現了磨機工作效率的提升。WANG 等[19]建立了礦石破碎中比表面積及裂紋面積的分形模型，進而推導出礦石材料的表面能計算方程，為破碎方法的選取及破碎過程的能量控制提供了理論基礎。胡松等[20]發現煤塊在單軸壓力載荷下，隨著應力增加，煤表面分形維數呈先緩慢增大后急劇增大的非線性關系，從微觀層面解釋了煤表面結構在不同應力應變下的變化規律。

礦石顆粒的碎裂通常是逐級變化的，其中每級破碎都伴隨著能量的消耗。目前，如何節能降耗仍是礦石碎磨領域的核心問題，對此部分研究者進行了碎磨過程能耗模型的探索。胡振中等[21]發現，傳統Bond能耗公式雖能較準確預測輥式破碎機和錘式破碎機在煤破碎過程中的能耗規律，但對顆粒入料及產物的細度模數有較高要求，隨后新建了基于能耗分形維數的能耗公式，經檢驗發現其對細度模數的選取要求不高，且能耗預測值與實際值擬合程度更高，可有效解決原煤破碎能耗預測難的問題。蔡改貧等[22]基于分形理論通過構建破碎能耗、礦石粒度分布、設備結構參數、破碎工作參數間耦合關聯，建立了低頻振動擠壓破碎能耗預測模型，其預測值與實際值擬合較好，可應用于新型板輥式低頻振動破碎機的研發，以計算礦石破碎所需要能量，從而選擇最優工作參數。

目前，礦石碎磨領域分形規律的部分研究成果已應用于實際生產，但多數研究仍停留在對分形維數與碎磨生產工藝參數間的定性分析方面，定量關系的相關研究較少，因此該領域仍有較大的研究、探索空間。總體而言，礦石顆粒形狀及碎磨能耗分形規律的研究有助于進一步優化生產工藝參數，其相關成果對未來工程應用亦具有重要指導意義。

2.3 分形理論在過濾中的應用

過濾是固液分離過程的重要環節，其操作過程可分為2 個階段：第1 個階段是過濾操作前礦漿懸濁液中礦物顆粒絮體沉降階段，第2 個階段是高濃度礦漿經過濾機加壓形成濾餅階段。在第2 個階段，除礦漿性質外，濾餅性質也可影響最終過濾效果。濾餅孔隙在平面的投影可看作是形狀不規則的多邊形。因此，可采用圖像分析法測量濾餅截面孔隙周長和面積，計算分形維數表征孔隙邊界復雜程度[23]。

式中，P(A)為濾餅截面孔隙周長；A為濾餅截面孔隙面積；D′p為濾餅截面孔隙分形維數，D′p越大，孔隙形狀越不規則，過濾效果越差。

濾餅分形結構與宏觀過濾行為密切相關，基于濾餅分形結構特性的調節有助于實現改善宏觀過濾效果的目標。來慶騰[24]發現，煤泥濾餅的上層孔隙率大、平均孔徑小、分形維數大，而下層濾餅孔隙率小、平均孔徑大、分形維數小，助濾劑的添加可針對性降低濾餅某些位置的分形維數，增大孔隙率，從而提高過濾效率。陳茹霞[25]研究顆粒性質對煤漿過濾效果的影響時發現，煤顆粒粒度越小，濾餅的分形維數越大，而顆粒粒度不均勻時，濾餅的分形維數從底層到表面逐漸增大，并由此提出為實現較好的過濾效果，應嚴格控制物料粒度組成并優化濾餅上層結構的思路。

綜上，探索不同條件下濾餅孔隙分形結構的變化規律，建立過濾操作與濾餅微觀分形結構之間的關系，有助于從微觀本質上解釋固液分離機理、實現礦物宏觀過濾行為的精準調控，并為難濾礦物過濾脫水設備的開發提供理論指導。

3 分形理論在調漿-浮選與絮體沉降中應用

調漿是浮選作業前的預處理作業，浮選是使目的礦物與脈石礦物分離的有效方法；沉降是過濾操作前的必要環節。在礦漿懸濁液體系中，微細礦物顆粒通過混凝的方式聚集形成絮體。若不考慮絮體的破碎情況，混凝過程可看作是微小顆粒結合成為小絮體，小絮體結合成大絮體，大絮體再聚集形成大絮團的過程，這在一定程度上滿足自相似性和標度不變性的分形特征(圖5)[26]。實踐表明，絮體分形維數相關研究有助于充分揭示礦漿混凝過程機理，對指導礦物加工工程實踐具有重大現實意義。

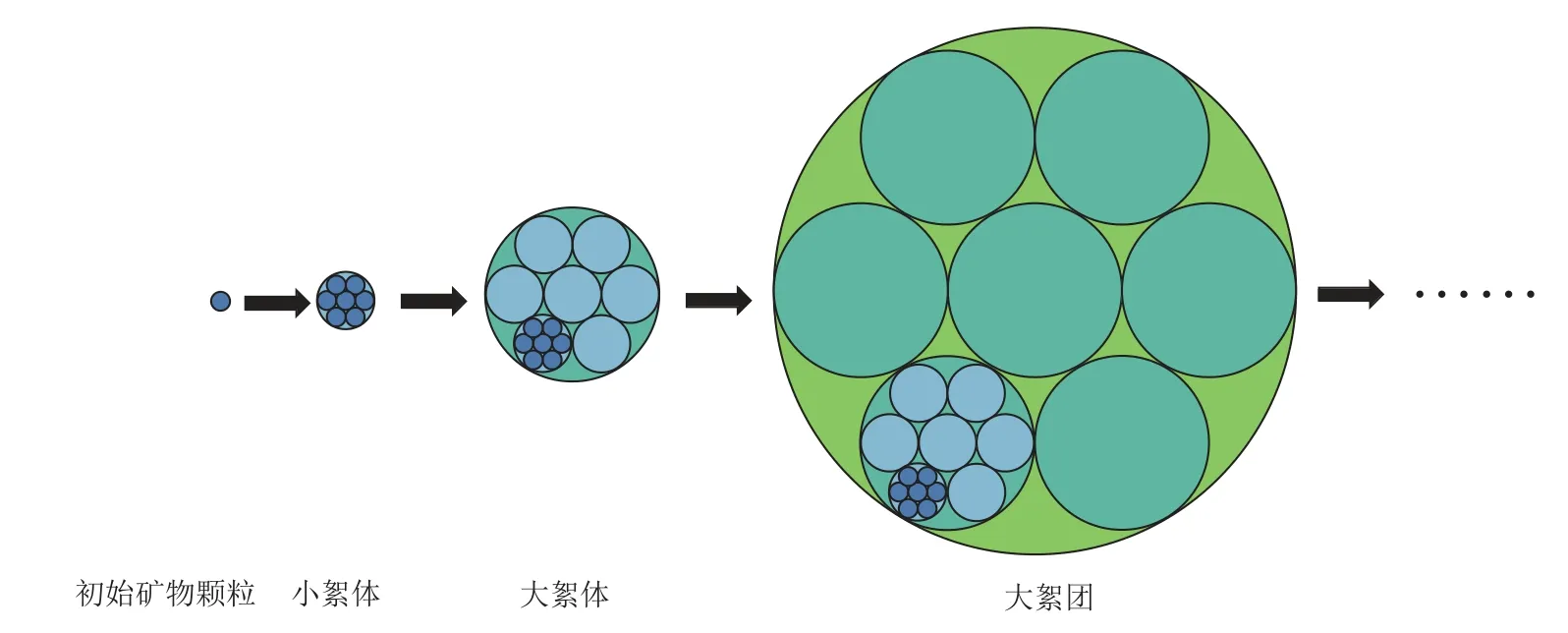
圖5 具有分形特征的絮體生長過程模型Fig.5 Floc growth process model with fractal characteristics

3.1 礦物顆粒絮體分形維數測量方法

絮體粒度分布分形維數可準確反映絮體群粒度分布，二維和三維分形維數可反映絮體結構密實程度。根據礦漿環境及絮體性質差異，學者們設計了不同分形維數測量方法。表1 為礦物加工領域常見絮體分形維數測量方法及其適用范圍和優缺點。由于不同測量方法的機理不同，分形維數差異可能較大，故對于同一體系內絮體間分維特性的表征宜統一測量手段。

3.2 基于分形理論的礦漿混凝行為

基于分形理論的混凝行為研究興起于水處理領域。由于礦漿懸濁液與廢水懸濁液某些性質相近，通常借鑒分形理論在水處理領域中涉及的部分研究方法與結論開展礦物加工領域礦漿懸濁液性質研究。

3.2.1典型混凝機理下絮體的分維特性

懸浮漿料體系中，多數微細顆粒可通過混凝的方式聚集，形成尺寸較大、結構較為復雜的絮體。凝聚和絮凝是混凝的2 種主要作用形式，壓縮雙電層、電中和、網捕卷掃、吸附架橋等是誘導混凝發生的基本作用機制。表2 為不同種類懸濁液在典型混凝機制下形成絮體的分維信息。相較于壓縮雙電層/電中和誘導形成的絮體，網捕卷掃作用下顆粒易被藥劑水解產物包裹，使形成的絮體空隙較少、結構密實，從而絮體三維分形維數較大；而吸附架橋作用下形成的絮體分支多，結構更加開放，其三維分形維數最小。網捕卷掃、吸附架橋作用下形成的絮體普遍具有網鏈狀結構，故對應二維分形維數通常較電中和誘導機制下絮體二維分形維數更小。

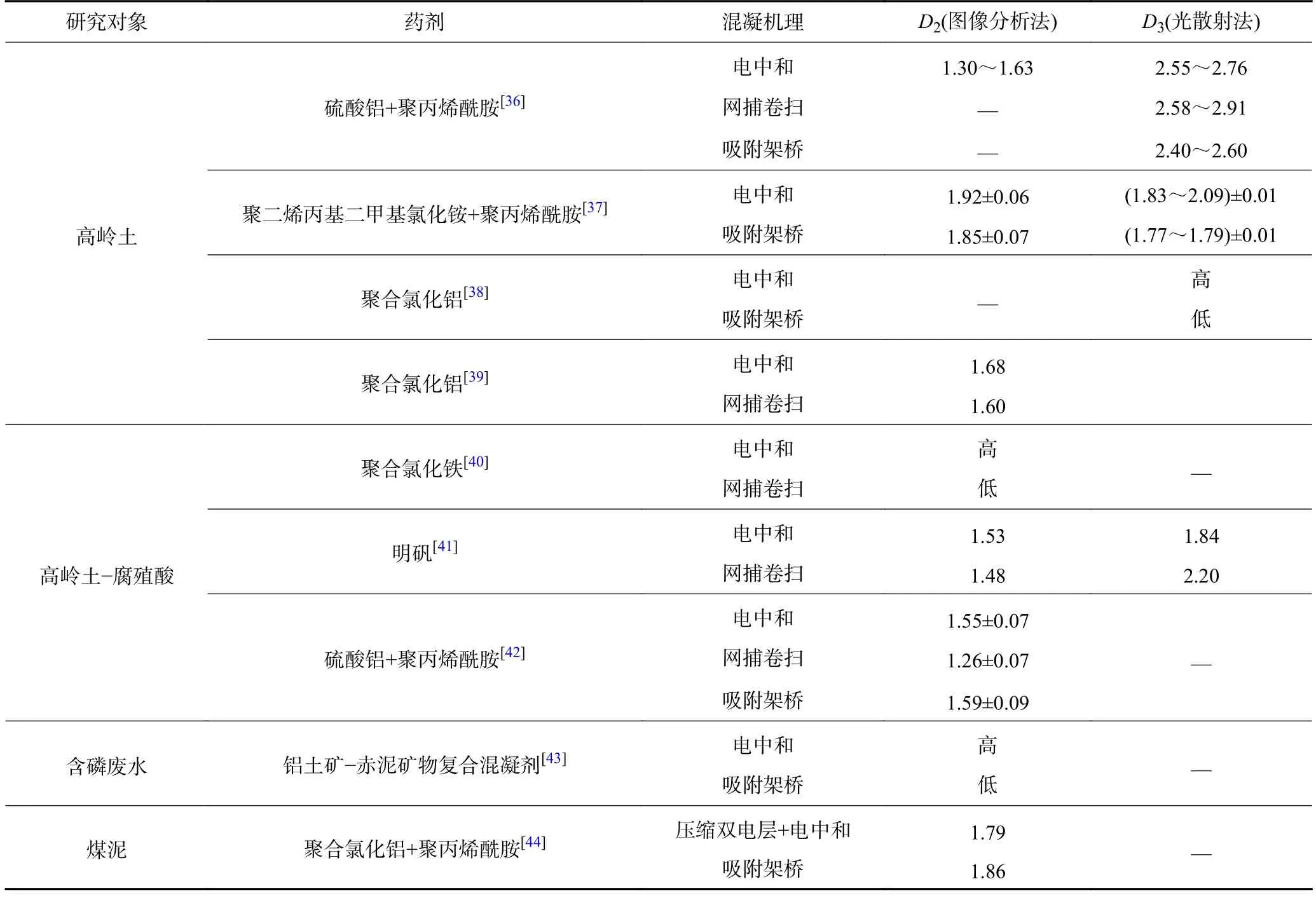
表2 典型混凝機理下絮體分維特性Table 2 Fractal dimension characteristics of flocs under typical coagulation mechanism

3.2.2分形理論在混凝動力學中的應用

隨著礦漿混凝研究的深入，絮體形成、生長及其結構動態變化的規律愈發引人關注。由于分形理論廣泛的適用性及其對絮體結構表征的直觀性，越來越多學者嘗試將分形理論引入顆粒混凝動力學研究過程中，以期更加深刻地揭示混凝過程中絮體空間結構及物理性質的轉變規律。

(1)絮體分形結構生長模型。為探究絮體生長過程對混凝工藝的影響，研究者們提出了3 類反映絮體生長特征的分形結構模型(每種模型包含單體凝聚和集團凝聚2 個亞類)。表3 為不同分形結構模型下絮體分形維數和結構特點。雖然不同凝聚類型下的絮體性質各異，但其分形維數間存在著一般規律：由于單顆粒比微絮體更易進入到絮體的內部，并使絮體密實度增加，故單體凝聚比集團凝聚形成的絮體具有更高的分形維數；由于各種模擬方法假設的黏結概率不同，反應控制模型考慮了顆粒間的相互作用，為了克服顆粒或微絮體間的斥力，需要更高的碰撞頻率才能形成絮體，故反應控制誘導的絮體分形維數區間較擴散控制誘導的絮體分形維更大。

表3 不同分形結構模型模擬形成的絮體分形維數及其特點Table 3 Fractal dimension and characteristics of flocs simulated by different fractal structure models

(2)基于分形理論的混凝動力學模型。混凝動力學模型旨在通過數學建模揭示混凝過程中顆粒性質隨時間動態變化規律，較為經典的有Smoluchowski 模型、群體平衡模型(PBM)等。通常情況下，流體中顆粒間碰撞機制主要有3 種：由分子熱運動引起的布朗運動、由水力和機械攪拌引起的流體剪切以及由顆粒尺寸和密度不同引起的差速沉降等，這3 種機制所形成的混凝模式均可影響顆粒碰撞函數β。傳統混凝動力學模型中綜合碰撞函數的計算僅是3 種碰撞函數間的加和，并沒有考慮3 者間潛在關聯性。而實際混凝過程中，絮體重組會使絮體粒徑、分形維數等性質發生變化，進而引起3 種碰撞函數及綜合碰撞函數的交互改變。將絮體分形維數引入顆粒碰撞函數β，即可得到分形理論耦合的混凝動力學模型[55-56]。表4對比了2 種經典混凝動力學模型引入分形維數前后的差異。混凝動力學研究過程中分形理論的引入能夠有效彌補傳統混凝動力學模型的不足(如忽略顆粒形狀、孔隙結構、不考慮絮體破碎重組等)，有助于深化對各操作變量引起的顆粒絮凝行為變化的內在機理的認識，對解耦顆粒混凝過程具有重大的理論意義。

表4 分形理論的引入對兩種經典混凝動力學模型的影響Table 4 Influence of fractal theory on two classical coagulation kinetic models

礦物加工調漿-浮選、沉降過程中，因作業目標差異，不同環節理想絮體結構也存在差異，如在尾礦沉降環節，為加強固液分離效率，理想絮體應粒度適宜，并具有一定抗剪切破壞能力；在浮選預調漿階段，為使目的礦物與脈石礦物充分分散并選擇性聚集，脈石礦物絮體強度應小于目的礦物絮體強度等。絮體其他結構特性與分形維數緊密相關，因此建立絮體不同結構參數之間的關系對礦物加工不同環節過程調控及指標優化具有現實意義。

(1)絮體密度。不同于單一顆粒，絮體內部往往存在大量空隙，在礦漿環境中空隙被液體占據而使絮體表觀密度降低。對于分形維數與絮體密度(孔隙率)之間的函數關系，一般認為絮體密度、粒徑與其分形維數滿足：

其中，ρe為絮體有效密度(在水中的密度)；dp為粒徑；D3=2.2～1.7[62]。故一般認為，絮體孔隙率越大，其密度越小，結構越松散，分形維數也越小。

(2)絮體粒度。絮體粒度與其分形維數間的關系可從單個絮體和絮體群2 方面分析。對于單一絮體，普遍認為絮體越大，其內部包含基本粒子數越多，對應分形維數越小[63]。對于絮體群，CHELLAM 等[64]研究不同分形維數絮體的粒度分布曲線時發現：當Df=3 時，絮體粒度分布范圍較窄，但隨著分形維數的降低，絮體粒度分布逐漸變寬且平均粒度向增加的方向移動。故一般認為，絮體粒度分布分形維數和平均粒徑呈負相關，且當粒級范圍相同時，細粒級所占比例越大，對應粒度分布分形維數越大。

(3)絮體強度。絮體強度是其抗破壞能力的表征，其大小取決于組成絮體顆粒間結合鍵強弱、數量以及絮體大小、密實度等性質。實際上，針對絮體強度與絮體分維特性間關聯關系，YANG 等[65]將絮體視為黏性較高的流體，把強度、分形維數與非牛頓流體的賓漢切應力結合建立了關系式，最終得出了絮體分形維數越高，體系的賓漢切應力越大，絮體強度越大的結論。總之，分形維數越大的絮體，其內部結構越致密，組成絮體的顆粒間排斥作用越小，其強度也越高。

3.3 影響礦物顆粒絮體分維特性的因素

3.3.1藥 劑

化學藥劑被廣泛應用于礦物加工過程不同工藝環節。考慮到絮體性質與礦物顆粒的聚集/分散狀態緊密相關，因此常見的影響顆粒聚集/分散狀態的藥劑，包括捕收劑、分散劑和混凝劑等，是相關研究的重點。其中，浮選捕收劑、部分混凝劑能夠通過強化礦物顆粒疏水，誘導顆粒通過聚團的形式形成具有不同分維特性的絮體。分散劑則能夠通過增強礦物顆粒間排斥作用或空間位阻效應，實現不同礦物顆粒間的分散(絮體的破壞)[66]。表5 為常見藥劑作用下不同種類絮體的形成機理及其分維特性。一般而言，單一電解質如AlCl3、CaCl2等主要誘導顆粒間發生壓縮雙電層作用，絮體分形維數隨藥劑用量的變化不明顯；有機高分子混凝劑主要誘導顆粒發生吸附架橋作用，其超過一定用量后易導致絮體分形維數降低；無機混凝劑的作用機理最復雜，其用量較低時顆粒間主要發生電中和作用，而當其濃度較高時可發生網捕和架橋作用。

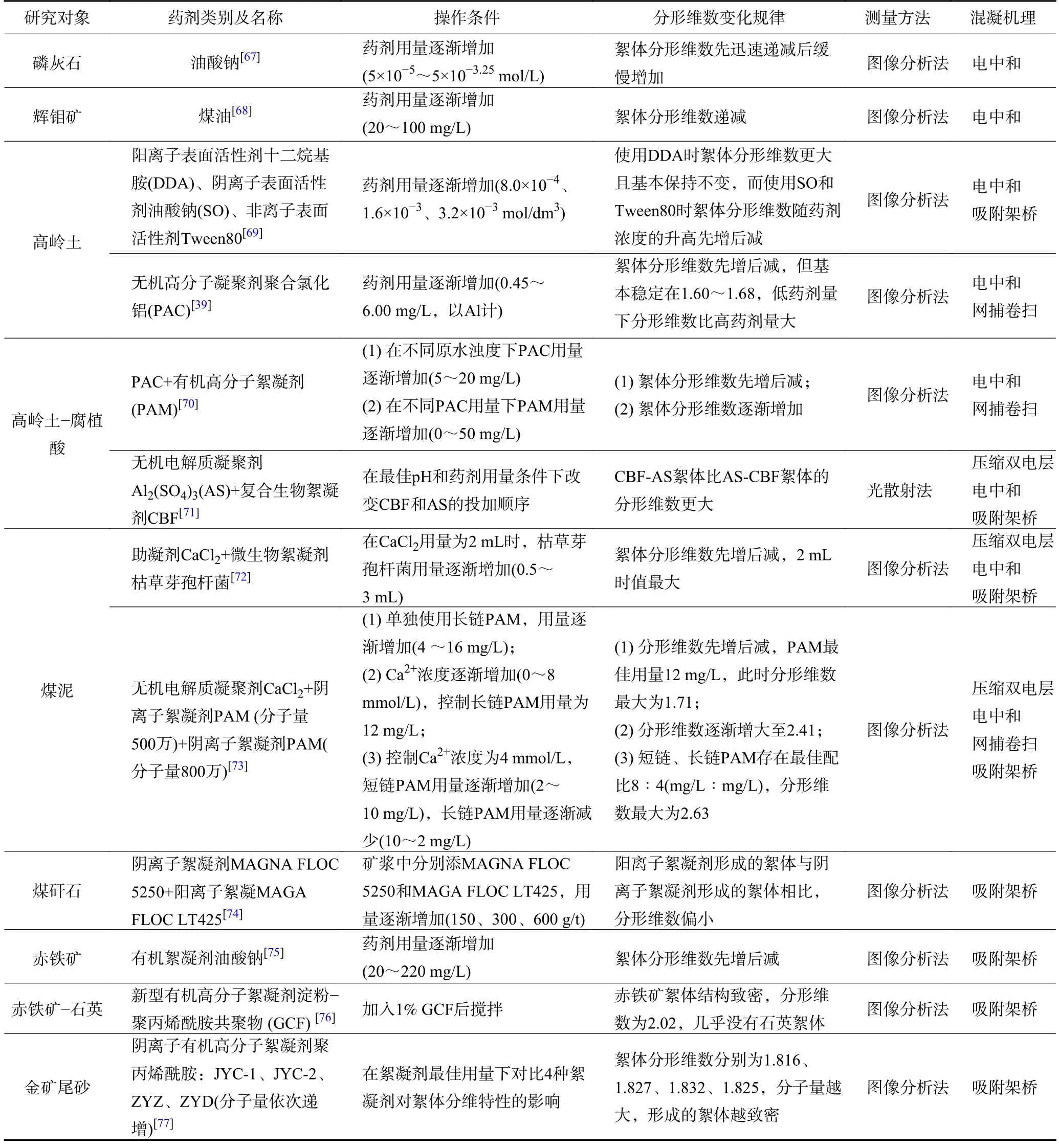
表5 藥劑添加對礦物顆粒絮體分形維數的影響Table 5 Effect of chemical addition on fractal dimension of mineral particle flocs

3.3.2礦漿性質

礦漿性質包括環境pH、溫度、鹽離子等因素均能夠通過影響顆粒聚集/分散狀態改變絮體分維特性。

緩沖溶液的pH是影響化學反應的主要因素之一，pH過高或者過低，都會對化學反應產生影響，很多反應，尤其是一些生化反應，往往需要在一定的pH下反應才能正常發生，比如在特定細菌的培養以及生物體內酶促反應等等，都需要穩定的pH,pH變化幅度過大就會造成細菌死亡，無法正常繁殖，也會使得酶的活性喪失，難以發揮其促使相關反應的作用，因此實驗室中經常需要配制一定濃度和一定pH的緩沖溶液，緩沖溶液的配制過程就涉及到緩沖對量取多少的問題，這就需要運用緩沖公式進行具體的分析。

(1) pH。礦漿pH 能夠通過影響礦漿中礦物顆粒表面電荷分布，進而影響顆粒聚集/分散行為，導致形成的絮體分維性質改變。對于某些pH 敏感型混凝劑，不同pH 條件下其水解產物不同，最終的混凝效果及絮體分維性質也存在差異。例如，溫海龍等[78]采用聚合氯化鋁處理高嶺土模擬廢水時發現，pH 約為6.5 時絮體分形維數最大，這是由于此時鋁離子水解的眾多產物中聚十三鋁(Al13)的含量最高，而Al13穩定性好且電荷密度高，有利于中和顆粒表面電荷形成穩定絮體。王興軍等[79]利用陽離子型聚丙烯酰胺處理煤氣化細渣懸濁液時發現，當pH 較大時絮體形狀不規則且分散，而隨著pH 降低絮體二維分形維數增大，這表明酸性條件下陽離子混凝劑混凝效果更強。

(2)溫度。礦漿溫度能夠顯著影響礦物顆粒、水、藥劑等多種組分的物化活性及其交互作用，造成顆粒混凝過程及絮體分維性質的差異化。劉云霞[80]發現，當溫度在20～80 °C 時，隨溫度升高煤泥水中絮體的分形維數呈現先增后減或逐漸增加的趨勢，并認為溫度的適當升高促進了顆粒布朗運動，提高了藥劑與顆粒間化學反應速率，進而強化了顆粒間凝聚；而溫度過高時，布朗運動加劇增強了絮體的水合作用，導致部分已形成的絮體再次破碎。XIAO 等[81]以硫酸鋁為混凝劑處理高嶺土懸濁液時發現，當礦漿溫度由28 °C 降至2 °C 時，絮體分形維數也降低，并認為溫度降低使得水的黏度增加，鋁鹽難以水解且水解產物與膠體顆粒的黏附作用減弱，導致形成的絮體更加松散。

(3)無機鹽離子。某些無機鹽離子對絮體分維性質有很大影響。WU 等[82]以用腐殖酸為沉淀劑，通過沉淀浮選法去除廢水中Cu2+、Pb2+、Zn2+等重金屬離子，發現隨著金屬離子質量濃度由10 mg/L 增至200 mg/L，絮體的分形維數顯著降低。XU 等[83]研究CaCl2對煤和高嶺土模擬的煤泥水絮凝行為的影響時發現，隨著Ca2+濃度增加，絮體分形維數增加。可見，外界條件不同，混凝過程中形成礦物顆粒絮體的分維特性間也存在顯著差異，礦漿物化性質的改變對調控顆粒聚集過程及絮體性質，實現選別指標的優化具有重要意義。

3.3.3水力學條件

混凝過程水力學條件能夠顯著影響顆粒聚集/分散效果，改變絮體分維特性，并對浮選預調漿及尾礦濃縮沉降等作業環節產生顯著影響。攪拌強度和攪拌時間是礦物加工過程中最為常見的水力學條件變量。

(1)攪拌強度。水力擾動能夠通過外加物理力場的方式調控體系能量輸入，顯著影響顆粒間的聚集/分散行為，進而改變顆粒絮體的分維特性。牛福生等[84]研究攪拌流場對赤鐵礦絮體的影響時發現，當攪拌轉速由700 r/min 增至900 r/min 時，絮體二維分形維數迅速增加；當轉速繼續增加，絮體分形維數變化較小，這是由于攪拌強度的增加可增大顆粒間碰撞、黏附概率，增加水流剪切力，有利于絮體形成。范桂俠[85]研究油酸鈉體系鈦鐵礦和鈦輝石聚集行為時發現，當攪拌轉速由0 增至2 100 r/min 時，2 種礦物顆粒絮體的二維分形維數均呈先增后減趨勢，但同一攪拌強度下鈦鐵礦絮體比鈦輝石絮體更加密實。

(2)攪拌時間。長時間的攪拌易導致已形成的絮體發生破碎。付嘉[86]利用納米磁性絮凝劑和助凝劑PAM 處理煤泥水時發現，在最佳攪拌轉速條件下，當攪拌時間在2～10 min 時，煤泥絮體分形維數逐漸增加并最終趨于定值。劉利等[87]在最佳攪拌速度下以PAM 為混凝劑處理煤泥水時發現，攪拌時間為10 s時絮體最為密實，而隨著攪拌時間進一步延長，絮體分形維數又逐漸降低。

由此可見，礦物加工礦漿混凝工藝環節存在最佳水力學條件，此時礦物顆粒絮體有最密實的結構。開展礦物顆粒絮體分維性質研究，有助于探明不同條件下顆粒聚集/分散行為，揭示絮體性質變化規律，進而實現對礦漿顆粒懸浮、沉降等工藝過程的精準調控。

3.4 分形理論在調漿-浮選及絮體沉降工藝中的應用

3.4.1在調漿-浮選中的應用

適宜的調漿-浮選條件能使目的礦物選擇性聚團、脈石礦物充分分散，進而實現目的礦物高效浮選回收。調漿-浮選過程中礦物顆粒間會發生復雜的聚團-破裂-重組現象，基于調漿-浮選過程研究能夠有效揭示調漿-浮選過程中不同顆粒間聚集/分散狀態的變化規律，深化對調漿-浮選強化礦物浮選作業的內在認識，甚至達到指導和調控浮選過程的目的。分形理論及其方法能夠有效用于調漿-浮選過程中礦物顆粒聚集/分散行為與絮體性質的研究，是揭示調漿-浮選過程中顆粒聚集/分散狀態的有效手段。

微細顆粒選擇性疏水聚團是實現不同種類物料浮選分離的前提。實踐中，通常基于分形理論探索不同操作變量下微細礦物顆粒聚集形態變化規律，進而指導后續浮選作業。金屬礦浮選領域，范桂俠[85]研究鈦鐵礦與鈦輝石選擇性聚團浮選時發現，相同油酸鈉用量條件下，鈦鐵礦絮體分形維數比鈦輝石絮體大，表明油酸鈉更有助于促進鈦鐵礦的選擇性聚團，從而實現鈦鐵礦的浮選分離；ZHANG 等[88]通過溶氣法浮選納米二氧化鈦顆粒時發現，當二氧化鈦絮體的分形維數最大時，對應浮選回收率最高。潔凈煤浮選研究領域，趙靜等[89]發現非極性油能夠使超細煤顆粒發生選擇性聚團，通過調節機械攪拌強度可改變煤顆粒絮體密實程度，當煤絮體二維分形維數最大時,浮選精煤產率最高且超凈煤產品灰分最低；梁龍[90]在研究煤的選擇性絮凝浮選時同樣發現，煤絮體分形維數的增加有助于提高浮選精煤產率的同時降低產品灰分。由此可見，調漿-浮選過程中，礦物絮體的分形維數性質與最終的浮選指標密切關聯，調漿-浮選過程中礦物絮體分形維數的深入研究有助于選別工藝流程的升級改造、促進綜合選別指標的提升。

3.4.2分形理論在絮體沉降中的應用

絮體沉降行為與其分維性質也密切關聯，基于分形理論探究不同絮體(群)沉降特性有助于深化對沉降過程的理解，相關研究成果為能夠調控礦物顆粒宏觀沉降行為提供借鑒。孫浩等[91]研究鉛鋅礦尾礦絮凝沉降行為時發現，分形維數大的絮體有較高的沉降速率；黃彥龍[92]以石英為載體，絮凝微細粒高嶺石尾礦時也發現了同樣的規律；李冬梅等[93]在研究架橋絮凝作用下泥沙絮體的形成過程時發現，絮體分形維數較大，密實度越高，沉降脫水性能越好。

此外，在過濾操作前高濃度礦漿懸濁液中礦物顆粒絮體的沉降階段，絮體結構能夠顯著影響過濾濾餅性質，進而影響最終過濾效果，例如ALAM 等[74]發現在混凝劑最佳用量下，煤矸石絮體分形維數大且強度較高，這有助于形成滲透率高、含水量適中的濾餅，進而提升過濾效率。故一般認為，當絮體分形維數較大時，其沉降性能更優越，反之則不利于沉降及過濾。需要指出的是，對礦物絮體分形維數的深入研究有助于選別工藝流程的升級改造、促進綜合選別指標的提升，但該方向的研究總體仍停留在實驗室階段，尚未實現規模性工業應用。

4 結語與展望

分形維數是分形的度量指標，用于描述分形體不規則程度及其在空間中的填充程度，在實踐中應結合分形體特征選取適宜的測量計算方法。

目前，分形理論已廣泛應用于礦石揀選、礦石碎磨、調漿-浮選、沉降及過濾等工藝環節的過程研究。礦石揀選領域，主要聚焦于礦石中有用礦物含量的分形分布規律研究；礦石碎磨領域，主要涉及碎磨過程礦石形態分形特征研究；調漿-浮選與沉降領域，主要體現在對礦漿混凝行為及不同條件變量下絮體分維特性研究；過濾領域，相關研究包括過濾參數、絮體分形結構和濾餅孔隙分形結構間的關系及濾餅結構探究等。分形理論研究深化了對礦物加工工藝過程的認識，實現了對不同工藝環節的過程調控與優化，并最終提升了綜合作業指標。

分形理論在礦物加工領域的應用為剖析各類具有自相似性等分形特征的工藝環節過程機理提供了新的研究方法。但不可否認，現有研究仍存在不足，且大部分相關研究成果尚未投入實際生產，因此分形理論在礦物加工領域仍有較大的發展空間。理論研究方面，由于基于分形理論的混凝行為研究發源于水處理領域，且礦漿懸濁液與廢水懸濁液性質間存在部分差異(如初始顆粒種類及粒度、絮體粒度、液體環境等)，尤其是混凝動力學及絮體分形結構生長模型研究方向鮮有選礦工作者涉足，因此可對該領域進行更深入的探索。工業實踐方面，分形理論的應用前景主要體現在礦山與選礦過程智能化方向：在礦石揀選領域，基于有用礦物在自然礦石中分形分布規律可預測揀選經濟效益指標，該成果可應用于選廠實際生產中，以提高生產效率，節約人力物力。在礦石碎磨領域，除人工優化設備參數外，還可考慮在破碎機出料口及磨機內部添加傳感器，對礦石粒度分布及顆粒形狀進行在線監測，通過算法分析顆粒粒度分布分形維數及形狀分形維數的變化規律控制碎磨過程，以將礦石精準碎磨至目標粒度，節約碎磨能耗。在過濾領域，可考慮在固液分離設備上添加圖像識別系統采集濾餅孔隙分維信息，以實現對過濾壓力及濾餅局部加藥的智能控制。此外，基于絮體分形維數的智能投藥系統已應用于水處理領域，即利用攝像裝置完成絮體圖像采集，再通過自編程序計算絮體分形維數，判斷絮體結構特征，完成自動加藥，實現了對水處理混凝過程的在線監控以及對絮體分形結構的靈活控制[94]，該研究同樣可應用于礦物加工調漿-浮選、沉降過程，除控制加藥量和加藥時間外，還可考慮實現對礦漿環境和攪拌條件的智能調控。

綜上，分形理論與傳統選礦理論、研究方法的高效融合是當前的發展趨勢，相關研究成果也必將有益于礦物加工技術的升級與智能化發展，為資源節約、環境友好、可持續發展的礦物加工工程體系的構建奠定基礎。