二面角問題的綜合幾何法運用

摘 要：本文對近三年全國高考Ⅰ卷的立體幾何主觀解答題的命題特點與考查形式進行總結(jié)，提出了通過綜合幾何法解決簡單的二面角問題的思路與步驟.

關(guān)鍵詞：新高考；立體幾何；二面角；綜合幾何法

中圖分類號：G632 文獻標識碼：A 文章編號：1008-0333（2023）22-0040-03

在歷年的高考數(shù)學中，立體幾何主觀解答題往往不會缺席，近三年，該題型的命題特點與考查形式呈現(xiàn)了一定規(guī)律.本文對此進行了總結(jié)，從結(jié)論來說，該題型提高了學生對綜合幾何法的掌握要求，并仍以二面角問題為難點設(shè)問.為讓師生更好地應(yīng)對該題型，本文提供了通過綜合幾何法解決簡單二面角問題的解題方案，并探討了綜合幾何法的學習意義與教學建議.1 新高考下二面角問題的命題特點

1.1 立體幾何主觀解答題的命題特點

近三年，立體幾何主觀解答題一般位于高考數(shù)學試卷的第18～20題的位置，設(shè)兩個小問.第一問往往是考查線面平行、面面平行、線面垂直、面面垂直等位置關(guān)系的證明.偶見考查棱錐、棱柱體積的計算，以及點到平面的距離計算，但頻率較前者要小.第二問往往是考查經(jīng)典線面角或二面角的相關(guān)計算，在廣東省選用的全國Ⅰ卷中，往往考查二面角的相關(guān)計算，亦有“全國愛考二面角，浙江愛考線面角[1]”的說法.

1.2 立體幾何主觀解答題的考查形式

根據(jù)《普通高中數(shù)學課程標準》的要求，學生應(yīng)能運用向量運算解決簡單的幾何問題，掌握基本空間圖形及其簡單組合體的概念和基本特征，能證明簡單的幾何命題并進行簡單運用.

簡而言之，即學生應(yīng)掌握解決高中階段立體幾何問題中常用到的綜合幾何法和空間向量法，并體會兩種方法的共性與差異.

回顧近三年的新高考，其立體幾何主觀解答題都能很好地貼合要求，考查了學生的綜合幾何法和空間向量法的掌握程度.但題目的圖形載體傾向于簡單幾何體（柱、錐、臺）或不規(guī)則幾何體[2]，少見長方體等易于直接建立空間直角坐標系的幾何體，這使得學生不能直接建系后依靠空間向量法解決問題.下面舉出兩個例子說明：

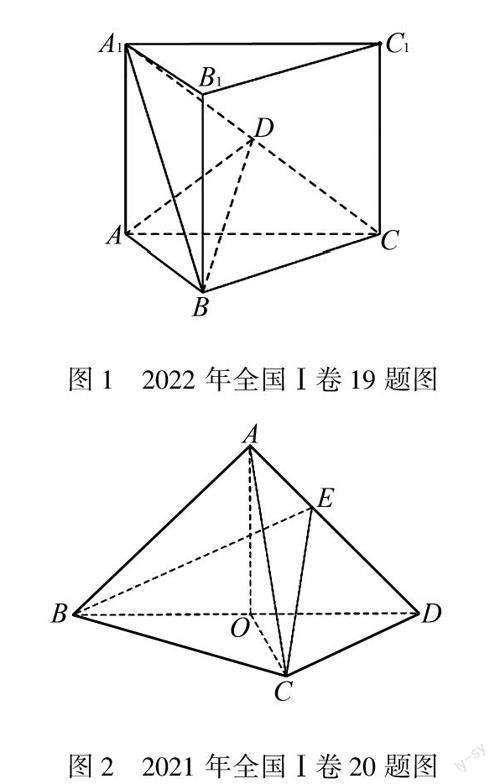
例1 （2022年全國Ⅰ卷19題）如圖1，直三棱柱ABC-A1B1C1的體積為4，△A1BC的面積為22.

（1）求A到平面A1BC的距離；

（2）設(shè)D為A1C的中點，AA1=AB，平面A1BC⊥平面ABB1A1，求二面角A-BD-C的正弦值.

例2 （2021年全國Ⅰ卷20題）如圖2，在三棱錐A-BCD中，平面ABD⊥平面BCD，AB=AD，O為BD的中點.

（1）證明：OA⊥CD；

（2）若△OCD是邊長為1的等邊三角形，點E在棱AD上，DE=2EA，且二面角E-BC-D的大小為45°，求三棱錐A-BCD的體積.

以上是近兩年數(shù)學高考全國Ⅰ卷的立體幾何主觀解答題.雖然圖形是簡單幾何體，但從題目的已知條件可知，學生不能直接建立空間直角坐標系進行解題，而是需要通過綜合幾何法證明出關(guān)鍵的線線垂直后才能建系，明顯提高了學生對綜合幾何法的掌握要求.

2 綜合幾何法解二面角問題

面對二面角問題，目前的教學以空間向量法為主.空間向量法對于解決二面角問題固然高效，但綜合幾何法解決二面角問題時，對于學習二面角這個幾何圖形有著較大的幫助.下面介紹綜合幾何法解決二面角問題的步驟、要點與示例.

2.1 解法要點

本法解決二面角問題，依然需要按照“作、證、求”四步完成.

第一步：找出與二面角其中一個半平面垂直的平面.

大多數(shù)二面角問題都會存在這樣一個平面，它與二面角其中一個半平面垂直，而這是使用本法的標志和開端（例如例1中，存在平面ABB1A1與二面角的其中一個半平面A1BC垂直）.

第二步：利用面面垂直構(gòu)造二面角的平面角.

此為“作、證、求”三步中的“作”.

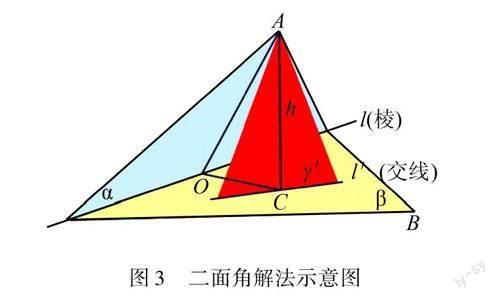
如圖3，假設(shè)第一步中，存在平面γ′垂直于二面角的其中一個半平面β，記A為平面γ′與二面角的另一個半平面α的其中一個交點.

過點A作h⊥l′，其中l(wèi)′=γ′∩β，h∩β=C.過點C在平面β內(nèi)作CO⊥l（l指二面角的棱），連接AO，則∠AOC為二面角A-l-B的平面角（或過點A在平面α內(nèi)作AO⊥l，后連接CO）.

第三步：證明二面角的平面角.

此為“作、證、求”三步中的“證”.

因為γ′⊥β，γ′∩β=l′，h⊥l′，

所以h⊥β.

又因為CO，l∪β，

所以h⊥CO，h⊥l.

因為CO⊥l，h⊥l，CO∩h=C，

所以l⊥平面AOC.

因為AO∪平面AOC，所以l⊥AO.

故∠AOC為二面角A-l-B的平面角.

第四步：求二面角的平面角.

此為“作、證、求”三步中的“求”.

在第三步中證明了h⊥l，所以△AOC是直角三角形.直角三角形中能夠運用勾股定理，也能簡單地計算其中一個內(nèi)角的三角函數(shù)值，這為最終解決二面角問題提供了極大的便利.

2.2 解法示例

例1 第（2）問解析

過點A作AE⊥A1B交A1B于點E.過點E作EF⊥BD交BD于點F.連接AF.

因為平面A1BC⊥平面ABB1A1，平面A1BC∩平面ABB1A1=A1B，AE⊥A1B

（識別出平面ABB1A1垂直于二面角的其中一個半平面A1BC），

所以AE⊥平面A1BC.

又因為EF，BD∪平面A1BC，

所以AE⊥EF，AE⊥BD.

因為EF⊥BD，AE∩EF=E，

所以BD⊥平面AEF.

因為AF∪平面AEF，

所以BD⊥AF.

故∠AFE為二面角A-BD-C的平面角.

（至此處已按照方法完成了二面角的“作”與“證”，如圖4）

因為AE⊥平面A1BC，BC∪平面A1BC，

所以AE⊥BC.

又因為直三棱柱ABC-A1B1C1中易證AA1⊥BC，AE⊥BC，AA1∩AE=A，

所以BC⊥平面ABB1A1.

因為AB，A1B∪平面ABB1A1，

所以BC⊥AB，BC⊥A1B.

因為AA1=AB，AE⊥A1B，所以A1E=EB.

又因為AA1⊥AB，易求A1E=EB=AE=2（引用本題第（1）問結(jié)果）.所以AA1=AB=2.

因為VABC-A1B1C1=4，AA1=2，

所以S△ABC=2.

所以BC=2.

因為∠EAF=∠BA1C，EF⊥BD，BC⊥A1B，

所以△BEF∽△A1CB.

所以EF=BC·BEA1C=2×223=63.

在Rt△AEF中

AF=AE2+EF2=2+23=263.

sin∠AFE=AEAF=226/3=32.

例2 第（2）問解析

過點E作EG⊥BD交BD于點G，過點G作FG⊥BC交BC于點F.連接EF.

因為平面ABD⊥平面BCD，平面ABD∩平面BCD=BD，

（識別出平面ABD垂直于二面角的其中一個半平面BCD），所以EG⊥平面BCD.

又因為BC，F(xiàn)G∪平面BCD，

所以EG⊥BC，EG⊥FG.

因為BC⊥GF，BC⊥EG，EG∩FG=G，

所以BC⊥平面EFG.

因為EF∪平面EFG，

所以BC⊥EF.

故∠EFG為二面角E-BC-D的平面角，∠EFG=45°.

（同上例，至此處已按照方法完成了二面角的“作”與“證”，如圖5）

又因為EG⊥FG，

所以EG=FG.

因為AO⊥BD，EG⊥BD，∠ADB=∠ADB，

易證△AOD∽△EGD.

所以DGGO=DEEA=2，AOEG=ADDE=32.

又因為BO=OD，

所以BGBD=23.

因為△OCD是邊長為1的等邊三角形，且BO=OD，

易證△BCD是直角三角形，∠BCD=90°，∠BDC=60°.

因為FG⊥BG，CD⊥BC，∠CBD=∠CBD，

易證△BGF∽△BCD.

所以GF=BGBD·CD=23.

所以EG=FG=23，AO=32EG=1.

所以VA-BCD=13·AO·S△BCD=13×1×32=36.

相較于代數(shù)問題，幾何問題更顯靈活性，學生在面對不同圖形載體下的幾何題目時，往往易出現(xiàn)不知從何入手的問題.盡管立體幾何問題浩如煙海，圖形載體千題千樣，但在實際教學中，應(yīng)該盡可能地將同類題型、問法歸類整理，總結(jié)出1～2條常見且行之有效的解題思路供同學們參考，減少學生常憑靈感解題的情況.長此以往，學生通過大量成功的解題練習，既能在不斷地練習中鞏固基礎(chǔ)知識、鍛煉解題技巧，又能增強立體幾何的學習信心.

參考文獻：

［1］ 朱成萬.高考立體幾何全國卷與浙江卷對比研究[J].中學數(shù)學月刊，2022（05）：49-52.

[2] 劉才華.2022年高考立體幾何復習及命題趨勢預測[J].中學數(shù)學雜志，2022（03）：54-61.

［責任編輯：李 璟］

收稿日期：2023-05-05

作者簡介：蔡毅錫（1992.6-），男，廣東省佛山人，本科，從事中學數(shù)學教學研究.