小學(xué)生數(shù)學(xué)說(shuō)題的內(nèi)涵和結(jié)構(gòu)分析

林祎珣

（福建省廈門市集美區(qū)后溪中心小學(xué)，福建 廈門 361021）

數(shù)學(xué)是一門比較抽象的學(xué)科，對(duì)于大部分小學(xué)生來(lái)說(shuō)學(xué)好數(shù)學(xué)還是有難度的，具體體現(xiàn)在以下方面：首先是概念的掌握上，比如周長(zhǎng)、面積、體積的概念，對(duì)于不同程度的孩子們來(lái)說(shuō)掌握起來(lái)是天差地別的；其次是體現(xiàn)在聽(tīng)課效果上，部分孩子課堂上好像聽(tīng)懂了理解了，但是一到做作業(yè)又什么都不會(huì)了；再次是知識(shí)遺忘和混淆，比如分?jǐn)?shù)和百分?jǐn)?shù)的聯(lián)系和區(qū)別；最后是各種常見(jiàn)錯(cuò)誤，比如單位換算、計(jì)算失誤、少算漏算等。開(kāi)展小學(xué)生數(shù)學(xué)說(shuō)題活動(dòng)，通過(guò)說(shuō)審題、說(shuō)思路、說(shuō)答題、說(shuō)反思等，引導(dǎo)小學(xué)生從解題走向析題、說(shuō)題，從而讓解題思維看得見(jiàn)，解題策略聽(tīng)得見(jiàn)，讓深度學(xué)習(xí)真發(fā)生。

一、小學(xué)生數(shù)學(xué)說(shuō)題的內(nèi)涵

學(xué)生說(shuō)題，是指學(xué)生生在認(rèn)真做題，精心準(zhǔn)備后說(shuō)出自己對(duì)數(shù)學(xué)題目的認(rèn)識(shí)與理解，闡述習(xí)題解答時(shí)所采用的思維方式，解題策略、方法及依據(jù)，進(jìn)而總結(jié)出經(jīng)驗(yàn)性的解題規(guī)律。學(xué)生說(shuō)題不是對(duì)解題過(guò)程的簡(jiǎn)單敘述，而是在說(shuō)題做題的過(guò)程中把新知識(shí)弄懂學(xué)會(huì)，與原有知識(shí)融會(huì)貫通，舉一反三，提升學(xué)生的思維品質(zhì)和數(shù)學(xué)素養(yǎng)。因此，在開(kāi)展小學(xué)生數(shù)學(xué)說(shuō)題活動(dòng)的過(guò)程中，應(yīng)注意以下三點(diǎn)：

（一）先解題后說(shuō)題

學(xué)生說(shuō)題必須先會(huì)解題，說(shuō)題所花的時(shí)間比解題更長(zhǎng)，而學(xué)生能夠花在數(shù)學(xué)學(xué)科上的學(xué)習(xí)時(shí)間是有限的，是非常寶貴的，所以教師應(yīng)該仔細(xì)分析教材例題和教輔習(xí)題和經(jīng)典考題，教學(xué)過(guò)程中要精心選擇典型題目作為學(xué)生說(shuō)題的素材。

（二）挖信息簡(jiǎn)過(guò)程

數(shù)學(xué)題目往往是靈活多變的，有些方法用起來(lái)運(yùn)算量大且復(fù)雜易出錯(cuò)，學(xué)生說(shuō)題時(shí)，教師要注意引導(dǎo)學(xué)生充分挖掘題目中的信息和數(shù)量關(guān)系，選擇合適的方法，可以通過(guò)說(shuō)一題多解，對(duì)不同解法進(jìn)行對(duì)比，初步引導(dǎo)學(xué)生體會(huì)“信息挖掘越充分，解答過(guò)程越簡(jiǎn)潔”。

（三）重聯(lián)系學(xué)新知

數(shù)學(xué)知識(shí)的學(xué)習(xí)環(huán)環(huán)相扣，新學(xué)的知識(shí)與學(xué)過(guò)的知識(shí)之間不僅有知識(shí)間的聯(lián)系，還有方法上的聯(lián)系。比如五年級(jí)所學(xué)的“分?jǐn)?shù)的意義和性質(zhì)”以三年級(jí)學(xué)過(guò)的“分?jǐn)?shù)的認(rèn)識(shí)”為基礎(chǔ)，長(zhǎng)方體體積公式的推導(dǎo)過(guò)程和三年級(jí)學(xué)過(guò)的長(zhǎng)方形的面積公式的推導(dǎo)過(guò)程類似，長(zhǎng)度、角度、面積、體積測(cè)量的本質(zhì)都是一個(gè)個(gè)計(jì)量單位的累加等等。所以我們要注重聯(lián)系，引導(dǎo)學(xué)生回憶，并“說(shuō)”出已經(jīng)學(xué)過(guò)的知識(shí)。

二、小學(xué)生數(shù)學(xué)說(shuō)題的結(jié)構(gòu)框架

本文以數(shù)學(xué)解題的相關(guān)研究和深度學(xué)習(xí)理論為基礎(chǔ)，結(jié)合上文內(nèi)容分析，總結(jié)出學(xué)生說(shuō)題的四個(gè)環(huán)節(jié),分別為：說(shuō)審題分析、說(shuō)解題思路、說(shuō)解題步驟、說(shuō)回顧反思。接著，根據(jù)義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)中的課程內(nèi)容和學(xué)業(yè)質(zhì)量要求，我們將學(xué)生說(shuō)題的四個(gè)環(huán)節(jié)再細(xì)分13 點(diǎn)，構(gòu)建學(xué)生說(shuō)題的結(jié)構(gòu)框架如圖1 所示。

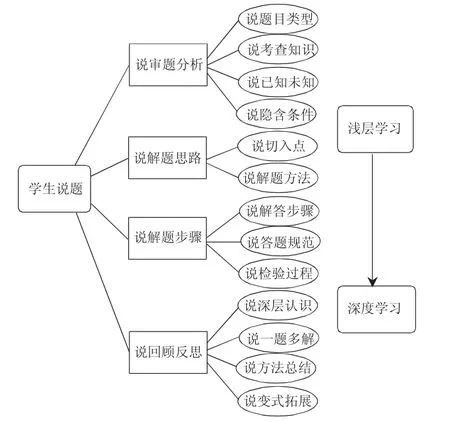
圖1 學(xué)生說(shuō)題結(jié)構(gòu)框架

（一）說(shuō)審題分析

弄清題意是正確解題的前提，也是有效說(shuō)題的保障。許多小學(xué)生由于年齡小玩心重，答題只追求速度，經(jīng)常沒(méi)有看清題意就開(kāi)始解答，今天上課老師教了“分?jǐn)?shù)乘法”，那么今天的所有題目一律用“乘法”來(lái)解決，一下就掉陷阱了。如果是說(shuō)題，那么就得“逼著”自己好好審題了。審題分析可以從題目類型、考查知識(shí)點(diǎn)、已知未知、隱含條件四個(gè)方面來(lái)說(shuō)。

下面主要從考查知識(shí)點(diǎn)和隱含條件兩方面展開(kāi)。

1.說(shuō)考查知識(shí)

說(shuō)考查知識(shí)也就是說(shuō)出題目所要考查的核心知識(shí)點(diǎn)以及相應(yīng)的數(shù)學(xué)方法，包括概念、公式、算理、算法、推理方法等。我們常說(shuō)“萬(wàn)變不離其宗，以不變應(yīng)萬(wàn)變”，意思就是題目再怎么變，考查的還是那些核心的知識(shí)與方法。

2.說(shuō)隱含條件

能否挖掘出題目中的隱含條件往往關(guān)系到能否正確解題。說(shuō)隱含條件時(shí)，可以說(shuō)一說(shuō)由已知的顯性的信息可以得出哪些結(jié)論，題目隱藏著哪些限制性條件（如單位是否需要換算，求現(xiàn)實(shí)生活中物體的表面積時(shí)求幾個(gè)面等），題目信息，比如文字語(yǔ)言、數(shù)量關(guān)系（這個(gè)條件怎么用數(shù)學(xué)符號(hào)或式子表達(dá)）等。

“說(shuō)審題”案例分析：

題目：明明拿來(lái)兩個(gè)長(zhǎng)度相同的長(zhǎng)方形紙條按圖2 放置，現(xiàn)在將這兩個(gè)長(zhǎng)方形同時(shí)向左右方向平移至圖3，相交部分和未相交部分的比是4:5。再平移至圖4，相交部分是未相交部分的,現(xiàn)在圖4 兩個(gè)長(zhǎng)方形紙條總長(zhǎng)是多少厘米？

圖2

圖3

圖4

說(shuō)題目類型和考查知識(shí)：這是操作中的數(shù)學(xué)問(wèn)題，考查的是應(yīng)用比的知識(shí)解決問(wèn)題，培養(yǎng)學(xué)生的觀察能力、計(jì)算能力和空間想象能力等。

說(shuō)已知未知：題目已知的數(shù)學(xué)信息為“第一次平移后相交與未相交部分的比是4:5，總長(zhǎng)72 厘米”，“第二次平移后相交與未相交部分的比是3:10”，未知的信息是“一個(gè)長(zhǎng)方形紙條的長(zhǎng)度”。

說(shuō)隱含條件：本題求的是第4 圖兩個(gè)紙條的總長(zhǎng)度，隱含著的條件其實(shí)是重疊部分一樣，空白部分也一樣。此外，還有一個(gè)隱含問(wèn)題就是“每個(gè)長(zhǎng)方形紙條的長(zhǎng)度是多少？”從圖3 中的72 厘米對(duì)應(yīng)4:5，可以分別求出未相交和相交部分的長(zhǎng)度，未相交部分的一半與相交部分的和就是一個(gè)長(zhǎng)方形紙條的長(zhǎng)度。

（二）說(shuō)解題思路

說(shuō)解題思路就是指說(shuō)分析與解答的過(guò)程，分析已知條件和未知條件之間的等量關(guān)系，采用適當(dāng)?shù)臄?shù)學(xué)方法得出問(wèn)題的“解”，題目的解題思路可以從切入點(diǎn)和解題方法兩個(gè)方面來(lái)說(shuō)。

1.說(shuō)切入點(diǎn)

說(shuō)解題的切入點(diǎn)，就是要說(shuō)清楚是如何提取題目中的有用信息，理解關(guān)鍵句，找到問(wèn)題的突破口的。

2.說(shuō)解題方法

小學(xué)數(shù)學(xué)中，常見(jiàn)的解決數(shù)學(xué)問(wèn)題的方法有分析法、綜合法、聯(lián)想法、歸納法和假設(shè)法，這些都是體現(xiàn)一般思維規(guī)律的方法，適應(yīng)面較廣。另外，還有一些適應(yīng)面較窄的作答技巧，比如解答選擇題時(shí)經(jīng)常采用的排除法和代入法。

“說(shuō)解題思路”案例分析：

題目：下面是六塊玻璃，用它們做一個(gè)魚缸，底面選用（），左右兩側(cè)選用（）、（），前后兩面選用（）、（）。這個(gè)魚缸共用玻璃多少平方分米？（玻璃的厚度忽略不計(jì)）

說(shuō)切入點(diǎn)：題目要做一個(gè)魚缸，魚缸只有5 個(gè)面，所以可以先確定底面再配側(cè)面，也可以先確定側(cè)面再配底面。

說(shuō)方法：解決這道題目我們可以采用分析法、假設(shè)法、觀察法，或者動(dòng)手操作的方法。

說(shuō)思路：我們先確定底面再配側(cè)面，可以配對(duì)挑出5 塊，或排除一塊。假設(shè)選擇D作為底面，那么就需要兩塊長(zhǎng)6dm，寬一樣的玻璃，有E 和F，那么剩下就需要兩塊長(zhǎng)5dm、寬3dm的玻璃，沒(méi)有就排除D，選擇剩下的5 塊，把5 塊玻璃的面積加起來(lái)就是魚缸的表面積了。

（三）說(shuō)解題步驟

有了解題思路，接下來(lái)就要通過(guò)具體解題步驟將過(guò)程清晰的呈現(xiàn)出來(lái)，這一過(guò)程包括答題規(guī)范和結(jié)果檢驗(yàn)。

1.答題規(guī)范

小學(xué)數(shù)學(xué)答題規(guī)范包括作圖規(guī)范和求解規(guī)范。結(jié)合《長(zhǎng)方體和正方體》的內(nèi)容，說(shuō)作圖規(guī)范包括用尺規(guī)作圖，用鉛筆作圖，添加的點(diǎn)要有相應(yīng)的標(biāo)識(shí)，看得到的線用實(shí)線，看不見(jiàn)的用虛線等。說(shuō)求解規(guī)范包括分步求解用序號(hào)標(biāo)注，從上到下、從左到右書寫，求周長(zhǎng)、面積、體積要寫明公式等。

2.說(shuō)檢驗(yàn)過(guò)程

說(shuō)檢驗(yàn)過(guò)程不僅包括計(jì)算結(jié)果的檢驗(yàn)，更重要的是檢驗(yàn)結(jié)果的合理性。

“說(shuō)解題步驟”案例分析：

題目：一個(gè)長(zhǎng)方體高增加5 厘米后變成一個(gè)正方體，此時(shí)表面積增加了1.4 平方分米，原來(lái)長(zhǎng)方體的體積是多少？

說(shuō)解題步驟和答題規(guī)范：第一步是單位換算；第二步求原來(lái)長(zhǎng)方體的底面周長(zhǎng)，增加的表面積= 高為5 厘米的長(zhǎng)方體的側(cè)面積，我們可以根據(jù)S側(cè)=C底h，列式140÷5=28（厘米）求出了底面周長(zhǎng)；第三步求出底面邊長(zhǎng)，能變成正方體說(shuō)明原來(lái)長(zhǎng)方體的底面是一個(gè)正方形，根據(jù)C正=4a，列式28÷4=7（厘米）求出底面邊長(zhǎng)；第四步求原來(lái)長(zhǎng)方體的體積，根據(jù)V正=a3，列式7×7×（7- 5）=98（立方厘米），由于增加5 厘米后是棱長(zhǎng)為7 厘米的正方體，所以原來(lái)長(zhǎng)方體的高是2 厘米，求體積時(shí)應(yīng)先求出高。

說(shuō)檢驗(yàn)過(guò)程：原來(lái)長(zhǎng)方體的長(zhǎng)寬高是7cm、7cm、2cm，表面積是154cm2，增加后成為棱長(zhǎng)7cm的正方體，正方體的表面積為294cm2，表面積正好增加了140cm2，符合題意。

（四）說(shuō)回顧反思

如何避免原題重做出錯(cuò)，做到解一題而通百題呢？一個(gè)簡(jiǎn)單有效的辦法就是解完題目后，靜下心來(lái)回顧與反思。

1.說(shuō)深層思考

對(duì)題目進(jìn)行深層思考，我們解完題后可以嘗試站在出題人的角度想想這個(gè)題目是怎么編出來(lái)的，在題目中設(shè)置了什么樣的“陷阱”是我們?cè)诮忸}中要注意避免的，題目中最巧妙的地方是什么等。

2.說(shuō)一題多解

很多數(shù)學(xué)題往往有多種解法，當(dāng)我們找出一種方法解答完成后不妨多想想還有其他方法嗎？把多種方法都想一想、說(shuō)一說(shuō)，不僅有助于提高我們思維的靈活性，更能發(fā)現(xiàn)解題的樂(lè)趣。

3.說(shuō)方法總結(jié)

學(xué)生說(shuō)題不應(yīng)該只是“解一題說(shuō)一題”，要“就一道題論一類題”，解完這道題要思考今后遇到類似的問(wèn)題怎么解決，說(shuō)題時(shí)要說(shuō)清題目所涉及的方法和規(guī)律。

4.說(shuō)變式拓展

題目變式可以從橫向拓展和縱向延伸兩個(gè)維度展開(kāi)，變式拓展是深化知識(shí)理解的有效途徑，同時(shí)對(duì)學(xué)生的綜合能力要求也是比較高的，可以從比較簡(jiǎn)單的變式開(kāi)始，比如變換已知條件和問(wèn)題。

“說(shuō)回顧反思”案例分析：

題目：一個(gè)長(zhǎng)方體水槽，長(zhǎng)10dm，寬8dm，高6dm，水深3dm。將一個(gè)棱長(zhǎng)4dm等正方體鐵塊放進(jìn)水槽后，這時(shí)水槽內(nèi)的水深是多少？

說(shuō)深層思考：1.水會(huì)不會(huì)溢出？答題時(shí)應(yīng)注意將結(jié)果和水槽高度進(jìn)行比較。2.正方體鐵塊會(huì)不會(huì)被完全浸沒(méi)？浸沒(méi)或者不浸沒(méi)對(duì)于等量關(guān)系“上升的水的體積=浸沒(méi)在水中的物體的體積”是否有影響？今后遇到類似問(wèn)題可否統(tǒng)一使用這一等量關(guān)系展開(kāi)思考？

說(shuō)一題多解：

方法一：先判斷是否完全浸沒(méi)，完全浸沒(méi)時(shí)上升的水的體積為80dm3，鐵塊的體積為64dm3，所以沒(méi)有完全浸沒(méi)，那么根據(jù)水的體積不變，底面積變小，可以列式10×8×3÷（10×8- 4×4）求出水的高度為3.75 分米。

方法二：根據(jù)等量關(guān)系“容器底面積和水面高度差的乘積= 浸沒(méi)在水中的物體的體積”，假設(shè)水的高度為H分米，可以列出方程“10×8×（H- 3）=4×4×H”，求出“H=3.75”。

說(shuō)方法總結(jié)：本題運(yùn)用了分析法或者方程法，根據(jù)水的體積不變開(kāi)始思考，在題目情境的變化中以不變應(yīng)萬(wàn)變。

說(shuō)變式拓展：本題是浸沒(méi)水中，那么如果反過(guò)來(lái)是提出水面呢？順著這個(gè)思路，題目可以拓展為“一個(gè)長(zhǎng)方體水槽，長(zhǎng)10dm，寬8dm，水槽里立著一個(gè)棱長(zhǎng)4dm的正方體鐵塊，這時(shí)容器里的水深為3dm，現(xiàn)把鐵塊輕輕向上提起10cm，那么露出水面的鐵塊上被水浸濕的部分長(zhǎng)多少厘米？”這一變式拓展題仍然可以根據(jù)原來(lái)的等量關(guān)系直接列方程求解。

三、結(jié)語(yǔ)

本文從說(shuō)審題分析、說(shuō)解題思路、說(shuō)解題步驟、說(shuō)回顧反思四個(gè)角度闡述小學(xué)生數(shù)學(xué)說(shuō)題的結(jié)構(gòu)框架，并提供了相應(yīng)的說(shuō)題分析案例。這四個(gè)角度彼此聯(lián)系，環(huán)環(huán)相扣，全面鍛煉學(xué)生的綜合能力。學(xué)生說(shuō)題活動(dòng)以學(xué)生為主體，以教師為主導(dǎo)。通過(guò)學(xué)生說(shuō)題，不僅可以培養(yǎng)學(xué)生的反思能力和實(shí)際解決問(wèn)題的能力，促使學(xué)生在說(shuō)題反思的過(guò)程中，不斷優(yōu)化知識(shí)結(jié)構(gòu)和方法體系，提升思維品質(zhì)，而且有利于教師獲得教學(xué)反饋，從而有針對(duì)性的地組織教學(xué)，促進(jìn)教育教學(xué)質(zhì)量不斷提升。