借“數直線”之形 促概念深度建構
——以“在直線上表示分數”為例

文|魏燕紅

數軸是小學課堂常用的基本的數學工具之一。小學數學教學中并沒有揭示數軸的概念，而是以“數直線”這一方式加以替代。“數直線”作為一種數形結合的學習工具，是帶給學生解決問題的方法和思路最直觀而有效的方式。在數的認識教學中靈活應用“數直線”，能起到化繁為簡、事半功倍的效果。

教材在分數教學中編排“數直線”，其編排意圖十分明顯，教材中的每一條數直線都承載著提升學生數學思維的作用。教師要充分挖掘數直線的使用價值，將數直線這一工具有意識地向學生逐步滲透，幫助學生建構認知，提升品質。

一、“1”“1”對應，開拓思維，正確理解數直線上的“單位”

單位“1”和分數單位，“單位”是認識分數的核心詞，單位的重要作用體現在能計量上。在數直線上表示分數，最關鍵的就是找到數直線中的單位“1”。因此，在教學中幫助學生理解單位“1”或分數單位在數直線上的表示方法，讓學生經歷分數先分后數的過程，是策略的核心。

1.溝通各類分數模型，正確認識數直線上的單位“1”

生活中一個圖形、一個物體、一個整體都可以看作單位“1”，在數直線上的單位“1”是舍棄了生活中形形色色的事物非本質屬性后高度抽象的結果，各種各樣的單位“1”在數直線上都只是0 到1這一段。更明確地說，在數直線上，單位“1”只有一個，具有唯一性，否則就會與一一對應的法則沖突，從而產生混亂。

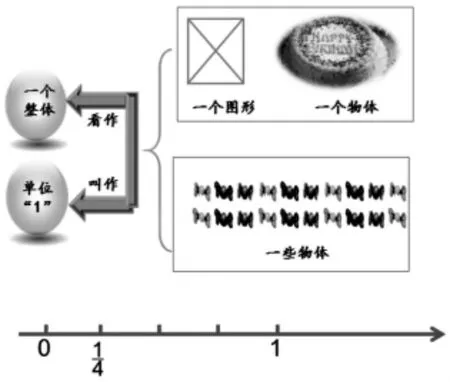
教學中第一次使用應該出現在分數的意義第二課時，在圖畫寫出分數說出意義的基礎上，通過對圖中的實物模型（一個蛋糕）、面積模型（一個圖形）、集合模型（20 顆糖）等抽象，讓學生概括出可以看作一個整體用自然數1 來表示，對應到數直線上的“1”，將學生的認識擴展到數直線上的1，能涵蓋的是生活中所有可以用“1”表示的事物，進一步讓學生明晰，生活中眾多的“1”都可以用數直線上的0 到1 這一段統一的單位長度來表示，可以把它們統稱為單位“1”。數直線上也可以表示各種分數，比如。把數直線上0～1 這段看作單位1，平均分成4 份，一份就是可以用數直線上的這個點表示。同理也可以找到

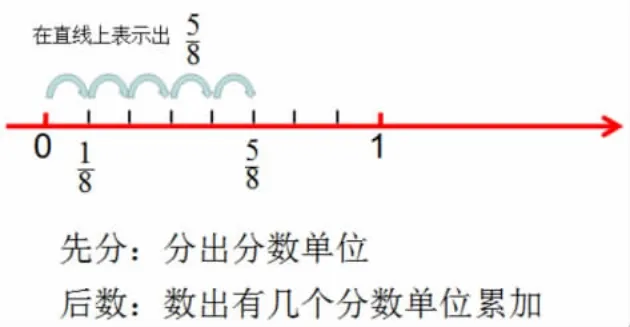
2.先分后數，體驗分數單位的計量過程，理解本質

分數是先分后數的一個數，單位“1”平均分成了幾份，其中的一份就是分數單位。數直線上的分數直觀地展現了分數單位的計量功能，先分知道了是什么分數單位，再數才知道有幾個這樣的分數單位，就是幾分之幾。教學中要注意引導學生先確定分數單位，再根據分數單位的累加功能尋找到分數在數直線上的對應點。

3.經歷單位累加，動態演繹區間定位

突出0～1 和1～2 區間的銜接。分數超過1，標在什么位置，是在數直線上表示分數的困難所在。突破這個難點，一定要突出“0～1”“1～2”之間的銜接。這個銜接延伸的過程是教學真分數和假分數的最直觀的載體。

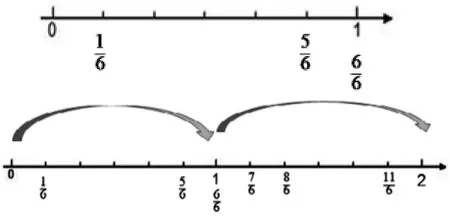
在學習《真分數和假分數》時，先出示0～1 的數直線，標出，接下去表示出，然后問這個點應該在哪里？學生能找到就是1 的位置，1 后面還有分數嗎？再繼續問在哪里？給學生思考的空間，經歷把目光從0～1的區間跨越到1～2 這個區間的過程，動態演繹數直線向右延伸的過程。兩個單位“1”累加，就是2，用自然數2 表示。思考：為什么在1 的位置，而必須在1～2 這個區間呢？學生會知道它比多一個分數單位，應該在，也就是1 的右邊一個分數單位的位置。再找出和。

這里有兩個目的：一是在數直線上找分數，親身經歷把數直線從一個單位延長到兩個單位、三個單位；二是隨著數直線的延長，豐富分數的范圍，為分數的分類做好鋪墊。

理解數直線上的整數是單位“1”的累加。在數直線上不僅分數單位可以累加，單位“1”也可以累加。兩個單位“1”累加，就用相應的整數2 表示，以此類推。數直線上相應的整數就是單位“1”的相應的累積，經歷數直線上的單位“1”的計量過程，溝通有幾個單位“1”就與數直線上整數幾對應，真正夯實學生對于數直線上的單位“1”的本質理解。

學了假分數和帶分數、整數的互化之后，我們可以引導學生先把假分數化為帶分數再來看。

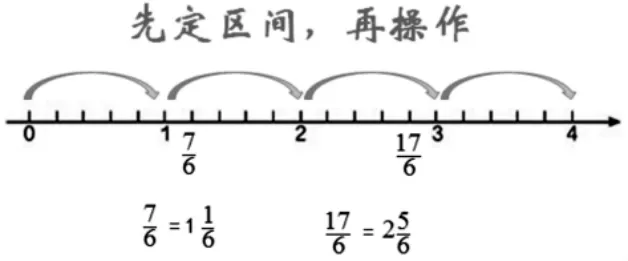
通過讓學生經歷0～1 與1～2的銜接過程，養成把分數按所在區間進行分類的習慣，一連串的強化訓練后就能突破難點，從而有效降低錯誤率。

4.借助等價分數，化繁為簡

例如：學習分數的基本性質之后，有這樣一道習題：

二、挖掘內涵，凸顯價值，構建數的集合

1.以數直線強化分數的意義在“數”上的拓展

分數既可以表示兩個量之間的關系，同時也可以表示一個具體的數值。我們需要幫助學生體驗分數的稠密性。

教師出示幾個真分數，上面這些分數分別是將單位“1”平均分成幾份，表示這樣的幾份，你能在數直線上找出這些分數的位置，并和大家說說你是怎么想的嗎？學生在說的過程中，課件出示這些分數對應的點，適時追問：在這條數直線上，除剛才這些分數以外，你還能找到其他的分數嗎？說說這個分數的含義并找到數直線上的大致位置范圍，像這樣的分數你找得完嗎？

通過以上的活動延伸，就可以讓學生比較深入地感知分數的稠密性，體驗分數的無限延伸。每個分數在數直線上都有相對應的點，學生對分數的認識，最初局限在0 到1 之間，在學生建立分數概念時，需要將學生的思維進行適當的拓展延伸。

學生根據以前的學習探究，已經能把真分數與數直線上的點進行一一對應了，但是由于學生之前沒有接觸過假分數，因此存在思維定勢。教學中憑借數直線無限延伸的特征，讓學生及時打破思維定勢，憑著整數和小數的學習經驗引導學生進行知識遷移，感知在1 后面還有無限多個分數，并且這些分數都比1 大。通過這個過程也可以讓學生更好地理解整數、分數、小數的聯系。

2.在數直線上感受累加思想，建構分數集合

人教版教材提供《真分數和假分數》的例題，從圓形的分割引導學生認識真分數、假分數以及帶分數。在學習的過程中，無論從假分數的出現，假分數的理解，帶分數的引入以及分數的分類，數直線都要比圓形面積分割更直觀、更自然。數直線是從原點出發向一個方向不斷增加或減少的，這個過程能讓學生體會并最大限度地感受累加的思想。所以我們把例題的思維載體改成數直線，為學生分數集合的建構提供更適合的思維支撐。

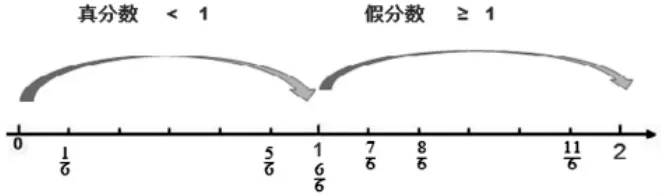
在多次試教中采用數直線作為學習材料，提供圖形表象支撐，并讓學生充分感受分數單位累加過程。學生不僅能很快找到分數單位，而且能在找的過程中真實地感受到假分數比1 大，位于1的右邊, 對建立假分數大于等于1 的表象，起到了形象支撐的作用。同時也讓學生直觀地感知到，分數以1 為分界線，分為兩大類：小于1 的是真分數，大于等于1 的是假分數，從而正確構建分數集合。

3.溝通數系之間的聯系，形成整體認知結構

（1）形成分數和整數序列，順應認知結構

課本中在直線上面填假分數，下面填帶分數的練習。

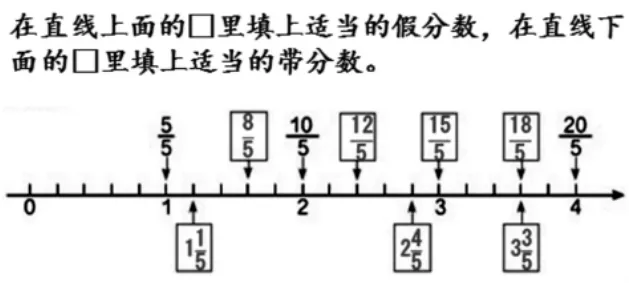
通過練習引導學生觀察發現，分子是分母的倍數的分數能化成整數，相鄰兩個整數之間再平均分可以細分出分數，而且存在無數種分法，感悟在相鄰兩個整數之間有無數個分數，實現分數意義的本質建構，把分數作為新數填充在整數之間，形成分數和整數的序列，學生的認知結構通過順應達到新的平衡。

（2）溝通整數、小數、分數之間的聯系，完善認知結構

數直線的形象支撐，可以幫助學生理清各種數概念的意義、計數方法、表示方法和分類等，進行比較思辨。整數的基本計數單位是自然數1，整數其他計數單位按十進制的規則生成。而分數是先確定單位“1”，再根據平均分的份數確定分數單位，平均分的份數不同，分數單位也不同。數直線借助圖形表征數概念，豐富學生對數的形象感知，引導學生在整體建構層面上理解和把握數的概念，進一步完善認知結構。

我們要深入理解數直線的內涵，挖掘其教學價值，拓展其應用范圍，發揮數直線的作用與功能，幫助學生建立大數學觀，培養學生的數學素養。