回顧與溝通，促進模型構建

楊建明

教學內容：數學人教版六年級下冊第六單元P87例4、例5。

教學過程：

一、導入新課，揭示課題

1.（幾何畫板演示立體圖形的生成過程）師：仔細觀察，你發現了什么？你能用幾個字總結一下嗎？引導：剛才我們看到的過程其實可以用12個字來概括：點動成線、線動成面、面動成體。

2.揭示課題。師：點、線、面是立體圖形的基本元素，這節課我們一起來進行立體圖形的整理和復習。（板書課題：立體圖形的整理和復習）

設計意圖：追本溯源，立體圖形其實是平面圖形的累加而成，點線面是立體圖形的基本元素。激活學生已有的知識經驗，為立體圖形的特征與模型構建提供載體。

二、操作探究，構建模型

活動一：自主整理，知識建構

1.師：回想一下，在小學階段，我們都學過哪些立體圖形？關于立體圖形你知道些什么？請大家拿出任務單，對照修改訂正。時間3分鐘）

2.同學們，在預習整理的過程中，你有什么疑問嗎？

思考：①長方體和正方體有什么相同點和不同點？

②圓柱和圓錐有什么相同點和不同點？

學生匯報交流。

3.游戲：我說你猜。（袋子里準備不同立體圖形）

師：看來大家對立體圖形的特征掌握得不錯！下面老師來檢測一下。隨機請學生從袋子里摸圖形，并向其他同學介紹摸到的感覺，全班同學猜是什么？

設計意圖：一堂單純的復習課很容易變得枯燥乏味，利用游戲激發興趣，不僅能強化立體圖形的特征辨識，有利于學生頭腦中建立立體圖形的空間模型，而且通過學生自主整理，師生交流、生生交流，將知識系統化，完善圖形的模型建構。

活動二：操作想象，建構模型

師：圖形與幾何的學習，想象力非常重要！

1.（出示一張長方形紙）看到這張長方形紙你想到了哪種立體圖形？

預設1：以邊為軸旋轉——圓柱。（師根據學生回答畫出來）隨機提問：有幾種旋轉方法？你能算出它的體積嗎？（板書：V=Sh）

預設2：圍起來，得到圓柱的側面。隨機提問：有幾種圍法？你能說說它的表面積怎么算嗎？（板書：S表=S側+S底×2）

2.（出示這張長方形紙）再問：看到這張長方形紙你想到圓錐嗎？（提示：先沿對角剪，再旋轉——圓錐）

追問：這個圓錐與剛才的圓柱有什么關系？怎樣求出圓錐的體積？（隨機板書：等底等高，V=１/3Sh）

3.師：同學們，一張小小的長方形紙咱們想到了許多，看來想象確實重要啊！請大家想想，如果把這個圓柱切一切、拼一拼，你想到了什么？

預設：長方體。（出示拼成的長方體）誰來說一說，這個長方體與圓柱有什么關系？

4.師：同學們，如果把長方體的長、寬、高都縮減為同樣長的線段，得到一個什么圖形？（正方體）隨機板書：特殊的長方體。你能說說它的公式嗎？

設計意圖：在數學建模教學中，讓學生經歷模型的誕生過程，在動手操作與匯報交流中讓學生溝通圓柱與長方體、正方體的聯系，體會轉化的數學思想。不僅有助于培養學生的創新意識，還有助于數學思想方法和解決問題策略的學習。

活動三：建立聯系，拓展模型

1.（還是剛才這張長方形紙）你能通過折一折，得到長方體或正方體嗎？（引導對折2次，圍成一個長方體或正方體）學生動手試一試。

提問：這張長方形的紙圍成了長方體的什么面？（側面）你能求出它的側面積嗎？（引導：底面周長×高）

2.觀察發現一：長方體S側=2ah+2bh、正方體S側=4a2、圓柱體S側=ch。無論長方體、正方體或圓柱體的側面積，都可以用：底面周長×高。

3.觀察發現二：三種立體圖形的體積公式，無論長方體、正方體或圓柱體的體積，都可以用：底面積×高。

4.補充：認識直柱體及其特征。

（1）怎樣求出下圖物體的體積呢？（師演示一個一個累加）師：你想到了什么方法？（2）介紹直柱體。學生辨別生活中的直柱體并說說可以怎樣計算它們的體積？

設計意圖：生活原型是數學建模的邏輯起點。在數學建模過程中，教師要依據數學知識的學科特質以及學生的年齡、心理特征，引領學生將生活問題抽象成數學問題，將學生實際生活中的素材引入課堂，讓學生運用“數學的眼光”去打量，用“數學的大腦”去考量，用“數學的語言”去描述。當認識了直柱體的特征以后，學生不難發現：直柱體的體積其實就是每層數的累加。利用這一模型，就很容易幫助學生理解統一公式了。

三、解釋運用，鞏固提升

1.選擇題：

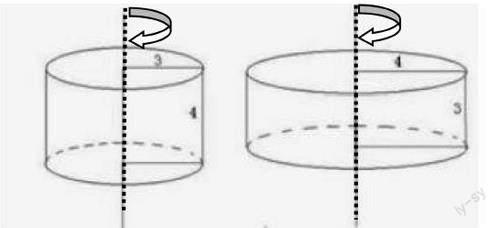
（1）小紅做了一個圓柱和幾個圓錐（如下圖，單位：cm），在圓柱中裝有水，將圓柱中的水倒入第（? ）號圓錐中，正好倒滿。

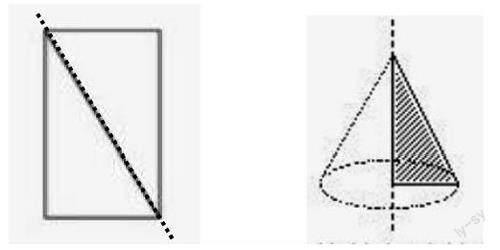
（2）下面（? ）圖形是圓柱的展開圖（單位：cm）。

2.判斷題：

（1）把圓錐的側面展開，得到的是一個三角形。（? ）

（2）把一段圓柱形木材削成一個最大的圓錐，削去的部分是原來的。（? ）

（3）圓柱的底面半徑擴大為原來的2倍，高不變，它的體積也擴大為原來的2倍。（? ）

（4）圓錐的體積等于圓柱體積的。（? ）

（5）等底等體積情況下，圓錐的高是圓柱高的3倍。（? ）

3.解決問題：一個密封的瓶子里裝著一些水（如右圖所示），已知瓶子的底面積為10平方厘米，請你根據圖中標明的數據，計算瓶子的容積是多少立方厘米？

設計意圖：鞏固訓練環節，設計內容基礎與提高并重，體現了層次性與多樣化。其中第3題引導學生自己提出問題，既鞏固本節課學習的內容，又培養了學生的問題意識。同時，教師要有意識地給學生提供數學建模的腳手架，豐富學生的數學建模方式、方法與策略，這樣久而久之，學生的模型意識就會逐漸培養起來。

四、反思回顧，思想延伸

1.回顧總結：通過這節課的復習，你印象最深的是什么？還有什么疑問？

2.贈言：在數學的天地里，重要的不是我們知道什么，而是我們怎么知道什么。

——畢達哥拉斯