基于改進多維粒子群的多無人機任務分配方法

彭鵬菲,龔 雪,姜 俊,鄭雅蓮

(1.海軍工程大學 電子工程學院, 武漢 430033; 2.海軍工程大學 作戰運籌與規劃系, 武漢 430033;3.武漢大學 水資源與水電工程科學國家重點實驗室, 武漢 430072)

0 引言

無人機(Unmanned aerial vehicle,UAV)[1- 2]因其結構簡單、造價低、情報收集迅速、易操作性和自主控制能力強等優勢,在軍事領域和民用領域廣泛應用。在民用領域,無人機的應用情景遍及地形勘測、事故救援和環境監測等方面;在軍事領域[3-6],無人機可進行目標精準攻擊、戰場態勢評估和指控通信等任務。多維粒子群算法[7]是由賽爾坎·希蘭茲等提出并于2016由彭鵬菲等人譯入,將其運用在模式識別中,并解決了從多位搜索空間無法尋得最優的難題,鑒于此將其引入本文并對其做出改進解決了復雜環境下的任務規劃問題。

如何應對多無人機任務規劃[8- 9]需求復雜多變、實時性要求高、解空間不確定,是當前研究的熱點[10]。在任務規劃熱點問題上,眾多學者通過蟻群算法[11-14]、離散鴿群算法[15]、粒子群算法[16]、細菌覓食算法[17]和改進人工蜂群算法[18]等群智能算法[19]對無人機任務規劃開展了深入探究,如張小孟等[20]通過改進人工蜂群算法,針對載彈數量約束編碼,構建多無人機任務規劃模型,得到多無人機火場滅火救援的分配結果。上述方法在相對程度上能解決多無人機任務分配問題,但在解決針對復雜戰場環境下多無人機任務規劃解空間的不確定性難題上存在一定缺陷,其缺陷主要表現在以下幾個方面:1)在多維搜索空間中,解空間的最優維度未知;2)忽略了任務需求也具有時變性特征。

針對以上算法所表現出的局限性,本文中提出了基于改進多維粒子群算法多無人機任務規劃方法:首先,在考慮復雜戰場環境因素的基礎上,建立了多適應度函數集任務決策模型;在多任務目標需決策的基礎上,引入多維粒子群的算法,通過動態維度變換,規劃出各無人機最優的任務執行序列,從而動態解決多約束條件下的任務規劃問題。最終,仿真實驗的結果表明:該任務規劃方法具有尋優能力強、尋優效率高的優點,不僅能有效解決無人機執行任務的高維度問題,而且能夠動態規劃執行任務的無人機數量。

1 多無人機多目標任務規劃模型

1.1 問題描述

假設有N個任務需要處理,則面向任務規劃的問題將抽象為一個無向圖G=(UAV,T),其中UAV表示無人機集群集合,則UAV=UAVi(i=1,2,…,NumA);T表示任務集合,抽象為T={T1,T2,…,Tn};且邊上的權重為多權重限制,表示為該無人機執行該任務時的所需條件及難易程度。

1.2 多目標函數

1) 總風險威脅函數

假設無人機執行任務時隨時間的改變情況為任務目標風險系數關于時間的正指數函數(隨時間的推遲,各種因素對無人機執行任務時影響逐漸加深且目標風險規避系數Vj也會隨之動態變化,且以一定的概率進行突變)則總風險收益為:

式中,Cj=ethjt為任務風險價值定量隨任務目標條件變化的函數,其中thi={th1,th2,…,thn}表示無人機在執行任務時,動態目標威脅的影響權重,Vj={V1,V2,…,Vn}>表示任務目標的風險規避系數集合,FAi={FA1,FA2,…,FAn}>表示無人機自身所具備的條件集合,ti為UAVi離開艦載平臺到目標Tj飛行時間。

2) 總位移函數

假設UAV在執行任務時,時間不作為要求,則無人機執行各個任務最短路徑視為多無人機任務規劃的目標之一。

其中,pathi為執行任務i的路徑代價。

3) 毀傷收益函數

UAV在對目標進行毀傷時,第j個無人機的使用武器裝備打擊第i個潛在打擊目標Dij時的擊中概率為pij,毀傷收益為wi,一臺無人機使用一個k類導彈所需要的成本為uik。

所以在無人機在執行任務時,以最大化的單位成本上的毀傷效果[19,21-22]為目標的目標函數可以表示如式(4):

1.3 約束條件

1) 單架無人機最大攜彈約束

其中,MaxMi為第i架無人機最大攜彈數量。

2) 任務執行情況約束

3) 無人機最大航程約束

pathi≤Disi

(7)

式中,Disi為第i架無人機的最大航程

4) 目標價值約束。

5) 毀傷閾值約束

無人機對任務目標進行火力打擊時,所產生的打擊效果為所有無人機對目標毀傷效果之和,執行的任務數量必須要超過一定的閾值,如式(9)所示:

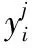
1.4 目標威脅系數的動態評估

在復雜因素影響下,由于惡劣的氣象條件、高強度對抗、緊張的空域資源等復雜戰場環境下,無人機執行任務將面臨地形、雷達探測、電子對抗、防空火力、禁飛區等飛行威脅區域。因影響無人機執行任務的因素太過復雜,根據專家系統量化[23]目標點的危險系數Threateni={th1,th2,…,thm}>,并對目標點的威脅系數進行實時評估,以確保在最大程度模擬真實復雜的飛行環境。位點變異概率mutation,每一個位點的目標點的威脅系數都有mutation概率發生變異:

thi→1-thi,i∈(1,2,…,m)

2 改進的自適應多維粒子群算法

2.1 多維粒子群算法

多維粒子群(MD PSO)[7]通過固定維度的標準粒子群(PSO)過程進行跨維傳遞,因此,在最優維數未知的多維搜索空間中,粒子可同時尋找位置最優解和維數最優解,從而無須預先設置固定維度d,因此,MD PSO算法在(Dmin≤d≤Dmax)的維度范圍內尋找位置和維度的最優解。

2.2 適應度函數集的設計

傳統的多維粒子群算法僅有一個適應度函數,若是有多個約束條件,則采用權重分配的方式衡量約束條件的重要性,但是戰場問題往往復雜多變,權重分配的適應度函數不能從根本上解決實時戰場問題,為此,本文通過設計適應度函數集,使得種群智能權衡復雜的戰場環境,最后通過全局尋優得到任務規劃最優的方案。則目標適應度函數集為:

F=fi,i=1,2,…,N

式中,fi表示第i個適應度函數。多個適應度函數作為粒子導向的限制因素,共同制約粒子在復雜戰場環境下的最優適應度。

2.3 適應任務時變性的目標函數

無人機在執行某個任務時,下一個任務的價值特性隨著時間的變化而變化,此時,假設該無人機執行的任務序列為T={T1,T2,…,Tm}>,則任務時變性需求的設計為:

式中,A表示平衡常數,Ci=ewt表示為任務價值定量隨任務目標條件變化的函數。由此,依據此結構,適應度函數,能解決任務需求具有時變性特征的問題,從而不斷地更新無人機執行任務的最佳序列。

2.4 基于高斯變異的自適應權重變化

為了進一步提高算法的求解精度,本文中設計了基于高斯變異的自適應權重,該算法在每次種群更新前,先對其父輩種群粒子的適應度值進行計算,通過比較每一個父輩粒子與種群全局最優適應度的大小關系,自適應改變慣性權重,均衡了算法全局搜索和局部搜索的能力。

則該算法的權重更新策略如下:

1) 計算全局最優適應度值和上一代種群最優適應度值。

2) 若當前種群適應度值優于上一代種群最優適應度值則采用式(11)進行更新權值:

wt=wmax*α

(11)

3) 若當前種群適應度值優于全局最優適應度值則進行基于高斯變異的自適應權重更新,如式(12)

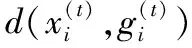
2.5 進化學習因子

學習因子是粒子群算法中的核心參數。本文采用的多維粒子群算法通過比較當前粒子的適應度值和種群的平均適應度值動態調整學習因子如式(14)。

C1隨迭代步數的增加遞減,而C2則與之相反。該策略使粒子在迭代前期更注重粒子本身的歷史軌跡,而迭代后期則更注重種群的位置信息。

3 面向任務序列的多維粒子模型

PSO算法只能用于求解簡單約束,存在目標函數單一且決策維度固定的問題。針對在多約束條件下,多目標函數且目標需以動態維度求解的多無人機任務規劃問題,本文采取一種基于整數編碼的改進多維粒子群算法,用以解決多約束限制的任務規劃問題。由于目標任務屬性不斷改變無人機執行目標任務維度,從而需動態規劃執行任務的無人機數量,其核心包括種群初始化、全局優化階段、更新迭代階段、粒子位置優選階段等方面。本文所提出的面向任務序列的多維粒子模型的多無人機任務規劃方法,總體執行步驟如下:

Step1:進行種群初始化、全局最優維度初始化以及全局最優適應度初始化等操作。

Step2:循環遍歷粒子群,假設當前粒子為a,進行如下操作:① 計算當前粒子a的個體適應度;② 進行全局尋優操作;③ 更新當前粒子a;④ 粒子a是否在粒子群中,若“是”,則返回步驟①,若“否”則進行Step3。

Step3:進行迭代更新操作。

Step4:判斷是否達到循環退出條件,若“是”,則進行Step5,若“否”則返回Step2。

Step5:輸出規劃結果。

面向任務序列的多維粒子模型的流程如圖1所示。

3.1 種群初始化

首先初始化n維種群,每一個種群根據無人機及任務目標的序列信息,隨機生成一個n維整數序列(M1,M2,…,Mn),進一步地,進行目標編碼,種群中每一個粒子都代表一個潛在的解,其中編碼數量小于等于目標數量。

3.2 全局尋優階段

在種群初始化后,開始全局尋優。本文采用適應度函數集限制粒子群的導向,種群通過智能權衡目標進行全局尋優,最終尋求多個適應度函數的最優向量及最優維度。

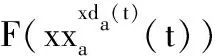
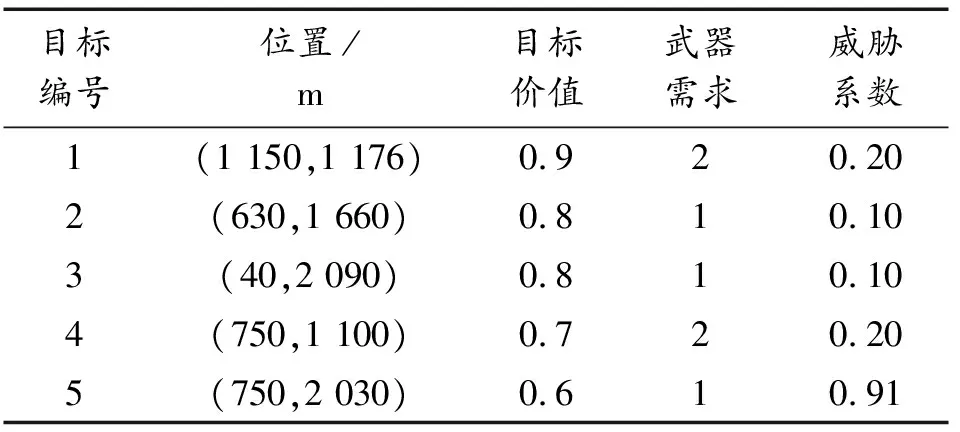
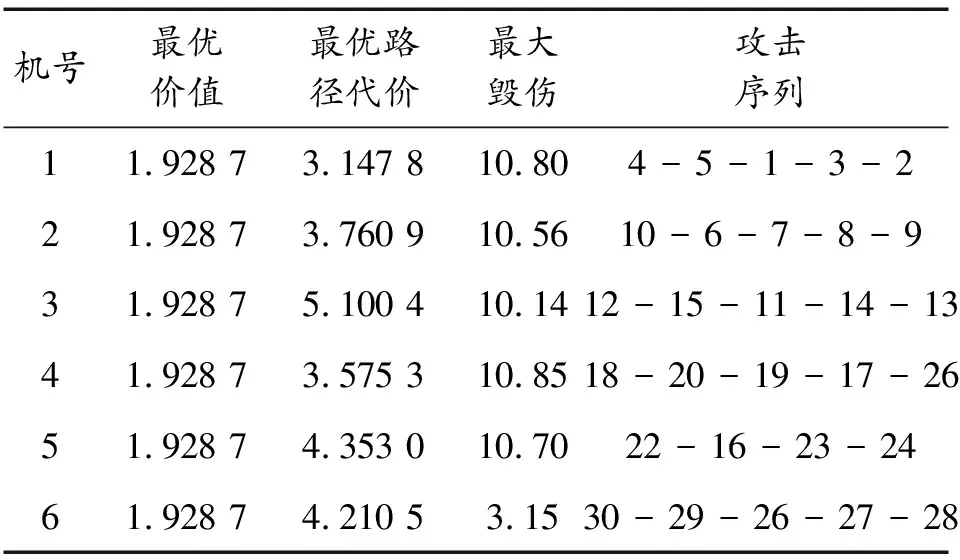
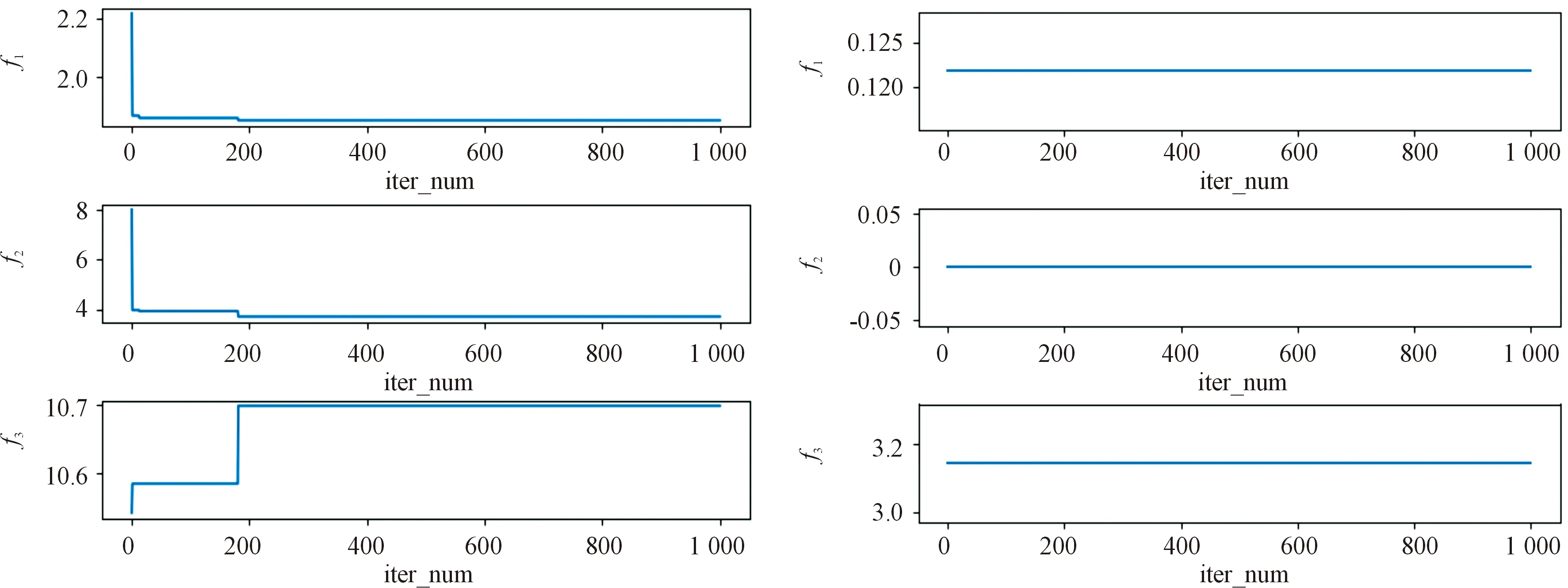
Step1:計算value,value_before,value_except,若value

Step2:更新個體最優粒子位置向量;

Step3:若value

Step4:若value

Step5:若value

最終,通過全局尋優模塊,不斷更新維度,快速精準地找到粒子最優位置以及最優維度。

3.3 更新迭代階段

經過全局優化后,種群的規模隨著全局最佳維度的變化而變化,種群的位置維度也隨之改變,則進入種群的更新迭代階段,執行步驟如下:

Step1:更新所有粒子的位置維度xda;

Step2:更新所有粒子的速度維度vda;

則經過整數編碼更新后,對上述步驟依次進行更新[7]。

3.4 位置更新策略

位置更新策略[7]是更新迭代階段的關鍵,它決定了粒子是否能跳出局部最優,實現全局最優。位置更新策略的步驟如下:

Step1:計算種群當前個體粒子當代適應值,記為value_a;

Step2:若value_a小于種群個體最優粒子適應度值(fitness_value),則進行Step3,否則不更新當前個體粒子位置;

Step3:更新種群最優粒子適應值;

Step4:若value_a小于全局最優適應值(global_fitness),進行Step5,否則不更新當前個體粒子位置;

Step5:更新全局最優適應值;

位置更新策略的流程圖如圖3所示。

3.5 局部動態調整

在復雜多變的空域環境中,常常存在不可預料的威脅、以及突然的目標變化等情況,預先的任務規劃或將不能完成。因此根據戰場態勢變化,在預先全局規劃的基礎上,僅進行局部動態規劃,從而可縮小規劃空間、減少規劃時間。具體設計為:

1) 局部任務動態分配。首先,構建局部規劃的無人機基站,多個目標點的初始任務執行序列,然后基于改進于多維粒子群算法進行全局尋優,求解局部最優的任務執行方案。

2) 局部航跡動態規劃。采用多維粒子群算法規劃任務路徑,然后基于三次B樣條曲線法進行航跡平滑,規劃任務執行航跡,最終回到初始基站。

4 實驗分析

仿真實驗平臺為LAPTOP-QEHE6SH7處理器是11th Gen Intel(R) Core(TM) i5-1155G7 @ 2.50GHz 2.50 GHz,64位操作系統,基于x64處理器的聯想小新筆記本進行了本次實驗。編程工具為Pycharm,應用了Conda環境。

4.1 改進多維粒子群性能驗證

根據表1所示的測試函數在固定維度解空間下對算法性能進行測試,其中f1為離散測試函數,f2、f3為單峰測試函數,f4、f5、f6、f7、f8為多峰測試函數,fmin表示的該函數的最小值,參與測試的算法為改進多維粒子群算法、遺傳算法和標準粒子群算法。對3種優化算法進行多次試驗,其結果如表2所示,將結果歸一化,可以直觀反應各個優化算法的性能,圖4和圖5為各算法的進化曲線圖。

從表2、圖4和圖5可以看出,在較少的迭代次數下,改進多維粒子群算法較其他算法有較好的收斂能力。無人機任務分配對算法的實時性較高,因而,本文推薦采用改進的多維粒子群算法。

因為遺傳算法的魯棒性較強因而從表2的數據來看,其計算出的最優值和方差在一定的條件下是可以進行使用的但是其最優值的準確度較表1中列出的解較差,準確率不高。標準粒子群算法雖然計算速度快,運行時間較短,但是從表2來看它的準確度遠遠低于遺傳算法和改進多維粒子群算法,改進多維粒子群算法能在一定程度上繼承了尋優速度快的特點又有遺傳算法中魯棒性強的優點,因此對于實時性的無人機而言是一個相對比較好的選擇。

從圖4和圖5可以看出,隨著迭代次數的增加,改進多維粒子群算法能夠迅速找到最優解,與其他2個算法相比收斂速度快,算法運行效率高,對于復雜環境下的無人機任務分配的具有實時性的作用,能夠快速規劃至一個較好的方案。

從多維粒子群的性能來看,相較于標準粒子群和遺傳算法。① 計算函數最優值準確度較高;② 收斂速度更快;③ 穩定性較高。因無人機在執行任務時實時性要求較高,因而選擇多維粒子群算法來進行多無人機任務分配。

4.2 基于改進多維粒子群的無人機任務規劃驗證

4.2.1參數設置

假設有2艘艦船,一艘艦船承載5架無人攻擊機,現有30個需要火力打擊的目標點,每架無人機的最大彈載量為8,無人機屬性如表3所示。30個目標取前5個目標作代表,屬性如表4所示。為直觀反應任務規劃效果,在仿真實驗中,將無人機目標與目標間的距離作為路徑代價,2艘艦船分別從x軸和y軸出發,接引無人機。

表3 無人機屬性

表4 目標屬性

4.2.2實驗結果及其分析

根據表4的目標屬性,設計種群數量規模為30,實驗次數為100次,迭代次數為1 000。運用改進多維粒子群算法求解任務規劃后,所得的各UAV的最優價值,最優路徑代價以及任務目標的火力打擊序列的結果如表5所示。根據各無人機的屬性,圖6—圖8為種群尋優過程中適應函數隨迭代次數的變化。

表5 無人機任務規化序列

圖8 第五、六架無人機風險收益(f1),路徑收益(f2)和毀傷程度(f3)的變化

從圖6—圖8可以看出,隨著粒子的進化代數逐漸增加,適應度函數f1、f2隨著進化次數的增加逐漸變小且達到最小,f3是無人機毀傷程度的變化,隨著進化次數的增加逐漸達到最大,則粒子群在100步以內已經找到了全局最優解,使得f1、f2達最小而f3達到最大。圖10中無變化的曲線表示的是該無人機在最開始就尋得了最優值,隨著進化次數的增加f1、f2、f2就不在發生變化。

仿真實驗結果表明,基于改進多維粒子群的多無人機任務分配方法在復雜的戰場環境下能夠迅速尋得最優分配方案,并在進行實時的任務分配時具有一定的穩定性,能夠使得無人機在路徑代價最短和風險收益最低時達到最大的毀傷程度。

5 結論

針對多無人機任務規劃中任務維度空間解不確定的問題,提出了改進的多維粒子群算法:

1) 針對多維粒子群算法,運用任務目標整數編碼的策略,將任務目標序列化并應用于多維粒子群位置向量,并通過設計適應度函數集的方式讓粒子群在不同維度下智能尋優。

2) 依據任務規劃的特點,設計適應度函數集,動態限制種群趨向,讓種群基于戰場復雜環境智能決策粒子最優適應狀態。

3) 因任務環境復雜多變,基于無人機機任務時變性,在多適應度函數的條件下,設計出適應任務時變性的目標函數,用于全局粒子群的導向。

4) 基于高斯變異的自適應權重變化和進化學習因子的設置,使得粒子群能夠迅速而智能化的跳出各個維度下的局部最優值,并尋得最優維度下最優規劃方案。

5) 在考慮目標價值變性的基礎上,動態尋找任務執行的最優維度,解決多約束條件下任務規劃動態尋優的問題,實現多無人機任務規劃。

基于改進多維粒子群算法在一定程度上解決了最優維度未知的多維搜索空間解的問題,具備推廣和應用的價值,但是在進行位置更新時還是存在有陷入局部最優的風險問題,因此可考慮將遺傳算法和多維粒子群結合設置擾動機制,大幅度降低此風險。