基于RBFNN和改進RISE控制策略的無人直升機軌跡跟蹤控制
張浩然,李 濤,潘世豪,冒澤慧
(南京航空航天大學 自動化學院, 南京 211106)
0 引言
無人直升機 (UAH) 作為常見飛行器,具有垂直起降、空中懸停、原地轉向等優點。近年在眾多飛行器中脫穎而出,得到許多學者關注并被廣泛用于民用和軍事領域,例如:高空巡檢、情報收集、艦載作戰、精細農業和災害監測等[1]。然而,實際UAH具有欠驅動和復雜動力學等特性[2],是個強非線性和強耦合的系統,如何有效控制UAH按照給定軌跡飛行,是具有挑戰性的研究問題。
針對UAH控制研究,早期工作偏向于在平衡點上運行時的線性UAH模型進行分析與設計,主要方法包括PID控制、線性二次型調節 (linear quadratic regulation,LQR)等。例如,文獻[3]利用PID控制方法分別設計UAH系統的位置和姿態控制器,并通過模糊控制來調整PID控制器的各項參數。文獻[4]采用PI控制內回路升降速率,外回路則由高度偏差給出升降速度指令,從而進行UAH自動起降的高度控制。針對UAH姿態回路容易失穩問題,文獻[5]提出一種基于Ziegler- Nichols法則建立調節PD參數的姿態控制策略。文獻[6]中分別建立UAH橫向和縱向通道系統模型,然后利用最優LQR控制方法設計降維觀測器,并利用觀測結果設計UAH姿態控制器。文獻[7]針對UAH懸停狀態下的線性模型,采用LQR最優控制器對姿態角進行穩定性控制。總體而言,UAH線性控制方法雖容易分析與設計,但僅針對UAH處于平衡點或近平衡狀態情況下進行控制,而對于實際UAH強非線性和強耦合性的系統而言,尤其針對系統模型存在偏差和較強外界擾動時,使用基于平衡點的線性控制方法,控制效果將會下降甚至造成飛行事故。因此,采用基于非線性控制技術與干擾估計補償等方法對UAH進行控制,能大大提升控制性能。
近年來,研究人員采用反步法[8]、反饋線性化[9]、滑模控制[10]、魯棒控制[11-14]、自適應控制[15]以及神經網絡控制[16]等非線性控制方法設計UAH控制器。例如,文獻[8]采用廣義PD觀測器來估計UAH的匹配和非匹配干擾,利用反步法結合干擾觀測器,分別設計出UAH高度子系統、水平子系統以及偏航角子系統控制器。文獻[9]針對轉彎控制時UAH系統強非線性和強耦合性,對UAH模型進行反饋線性化,再根據等效系統設計了PD控制器。文獻[10]利用軌跡線性化結合滑模控制 (sliding mode control,SMC) 方法設計擾動觀測器,分別對UAH位置系統和姿態系統進行干擾補償和控制。而實際情況中,需要考慮外部干擾和模型不確定性等影響,因而需要聯合設計補償器和控制器確保UAH軌跡跟蹤誤差控制在盡可能小有界范圍內。
現有文獻解決系統不確定性和干擾抑制方法中,魯棒控制、自適應控制、神經網絡控制以及DOBC等被廣泛應用于各類實際控制系統中。例如,文獻[11]中首次提出RISE控制方法,以補償非線性系統模型不確定性。文獻[12]改進RISE非線性控制設計方案,考慮參數不確定影響,研究了四旋翼UAH漸近輸出調節問題。文獻[13]提出基于數據驅動的無模型魯棒控制方案,減小控制器對UAH動力學模型的依賴性,克服不確定性對控制精度的影響。針對UAH存在強不確定性,文獻[14]也提出一種魯棒控制律設計方法,與文獻[11-13]不同之處在于結合自適應技術,即以魯棒伺服LQR作為控制設計基礎,再利用L1自適應設計前饋控制器。同樣針對UAH系統不確定性和外部干擾問題,文獻[15]分別建立自適應NN控制器補償不確定性和二階擾動觀測器處理復合擾動,確保UAH跟蹤誤差漸近收斂。文獻[16]給出基于RBFNN和干擾觀測器的UAH吊裝系統滑模減擺控制方法。綜上,針對UAH不確定性和外部干擾控制問題,仍需提出并改進現有的控制方法,對提升UAH軌跡跟蹤控制性能具有重要理論和現實意義。
受文獻[11-12]中方法啟發,本文中針對UAH軌跡跟蹤控制問題,提出一種基于改進RISE控制策略,同時利用RBFNN估計UAH模型不確定性和外部干擾組成的復合擾動,建立新型UAH軌跡跟蹤控制設計策略。首先,建立非線性UAH系統模型,給出必要的假設條件和引理。然后,將跟蹤誤差作為RBFNN輸入信號,估計由模型不確定性與外部干擾所組成的復合擾動,以濾波誤差信號權重組合作為改進的RISE輸入信號,分別設計UAH位置回路和姿態回路控制器。其次,采用Lyapunov穩定性理論分析閉環系統穩定性,確保所提控制方案可使UAH閉環系統有界穩定,即獲得期望的跟蹤控制性能。最后,仿真結果說明本文中所提控制算法的有效性和優越性。
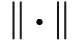
1 系統模型和問題描述
根據文獻[16],本文中建立包含模型不確定性和外部干擾的6-自由度中型UAH非線性系統模型,其中力與力矩作用采用了相應的簡化方式,動力學模型表示如下:
式中,P=[x,y,z]T和V=[u,v,ω]T分別表示慣性坐標系下UAH的位置向量和速度向量;Θ=[φ,θ,ψ]T表示機體坐標系中的歐拉角向量,W=[p,q,r]T表示角速度向量;Fb=[0,0,-Tm]T和Mb=[L,M,N]T分別表示作用在UAH機身上的外力和外力矩,Tm是主旋翼產生的推力,L、M、N分別是滾轉力矩、俯仰力矩和偏航力矩;Ir=[Ixx,Iyy,Izz]T為轉動慣量向量,m為UAH質量;Δf1和Δf2代表系統的模型不確定性,d1(t)和d2(t)為外部干擾;R(Θ)則是從機體坐標系到慣性坐標系的轉換矩陣[17],定義如下:
且H(Θ)代表姿態運動矩陣[17],定義為
定義x1=P,x2=V,x3=Θ,x4=W,可將動力學方程(1)轉化為以下形式:
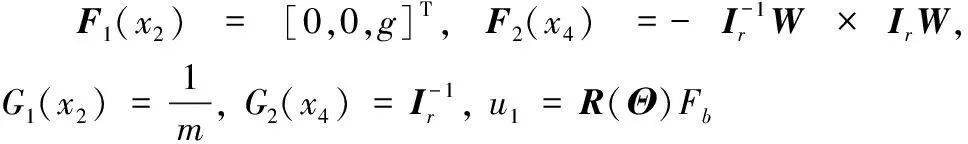
為了方便后文中控制器設計和閉環系統穩定性分析,定義位置參考軌跡向量和姿態參考軌跡向量分別為:x1d=[xd,yd,zd]T和x3d=[φd,θd,ψd]T,并引入以下的假設和引理。
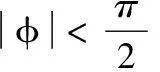
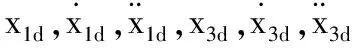
假設3[16]存在正常數σ1,σ2,σ3,σ4使得由外界環境引起的時變未知干擾d1(t)和d2(t)以及模型不確定性Δf1和Δf2均有界,即:
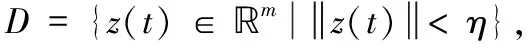
其中,U1(z(t))和U2(z(t))是連續的正定函數,U(z(t))是一致連續半正定函數,則有:
U(z(t))→0,t→+∞
(7)
這里z(0)∈S,其中區域S定義為:
且δ是滿足上述條件的正常數。
引理1[21]對于給定連續時間的未知函數g(x),如果具有足夠多的隱藏節點,則可表示為:
g(x)=W*TΦ+ε
(9)
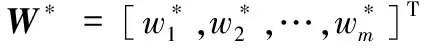
這里X=[X1,X2,…,Xn]是由n個信號組成的輸入向量,Cj=[C1j,C2j,…,Cnj]為中心點向量,j=1,2,…,J,其中隱藏層節點總數為J,d為高斯函數的寬度。
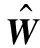
2 控制設計策略
本節針對UAH位置子系統和姿態子系統分別設計控制器。首先,設計位置回路的控制方案,控制器根據給定的參考軌跡對UAH位置系統進行控制;隨后,將位置控制器輸出進行變換,作為姿態控制器參考輸入信號 (偏航角參考值ψd已提前設定);最后,設計姿態控制器完成UAH姿態角的控制,具體控制框圖如圖1所示。
圖1 面向任務序列的多維粒子模型流程
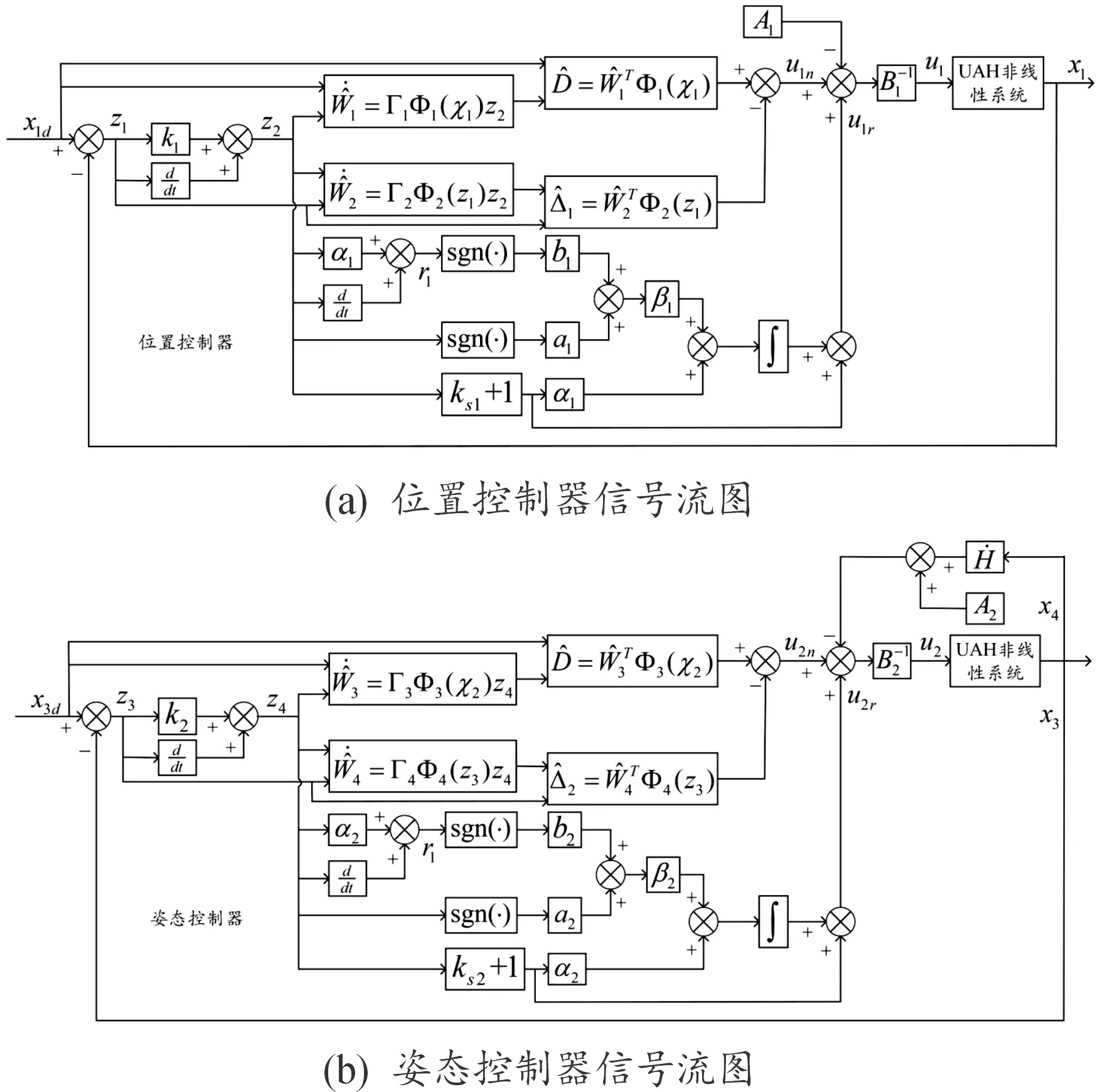
圖1 UAH軌跡跟蹤控制信號流圖
2.1 位置系統跟蹤控制
本節主要研究內容是為UAH位置回路設計控制律u1,從而得出位置跟蹤誤差閉環系統。
定義位置信號跟蹤誤差為
z1=x1d-x1
(13)
則位置回路的濾波跟蹤誤差:
其中k1和α1為待設計的正定濾波增益矩陣。
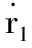
將式(4)和式(12)代入式(13)可得到:
其中A1=F1(x2),B1=G1(x2)為對應位置控制輸入u1的參數矩陣,Δ1=Δf1(x2)+d1(t)為由模型不確定性和外部干擾所組成的復合擾動。
定義2個輔助函數分別如下:
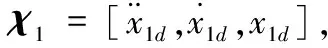
r1=D(χ1)+S1-A1-B1u1-Δ1
(17)
備注2D(χ1)是與已知參考信號相關的函數,其輸入輸出均僅與參考信號相關[23-24],且D(χ1)是關于χ1的連續時間函數,因此將χ1作為NN輸入信號,可減少測量噪聲對參考信號的影響。下文姿態回路中D(χ2)含義與此相同。
根據引理2,可用RBFNN對D(χ1)和Δ1進行逼近,并分別表示為
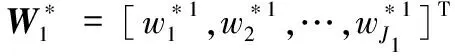
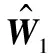
備注3模型不確定性和外部干擾會引起軌跡跟蹤誤差產生變化,利用跟蹤誤差變化情況可實時估計出UAH受到的復合擾動,而參考軌跡的測量時會產生少量噪聲,同樣也需處理,因此分別設計NN估計復合擾動和避免測量噪聲的影響。此外,J1和J2的值取決于其近似函數的復雜程度,函數越復雜,則需要的神經元個數就越多,且J1和J2的值無法準確獲取,需要不斷試驗選擇最優值,下文姿態回路關于J3和J4的解釋也與此相同。
位置控制器分2部分設計,其中控制器中涉及到NN部分的控制律設計如下:
基于RISE方法設計控制律時,將改進文獻[11-12]中設計方法,將z2和r1均作為符號函數的輸入并引入權重重新組合,即:

β1[a1sgn(z2(τ))+b1sgn(r1(τ))]}dτ
(22)
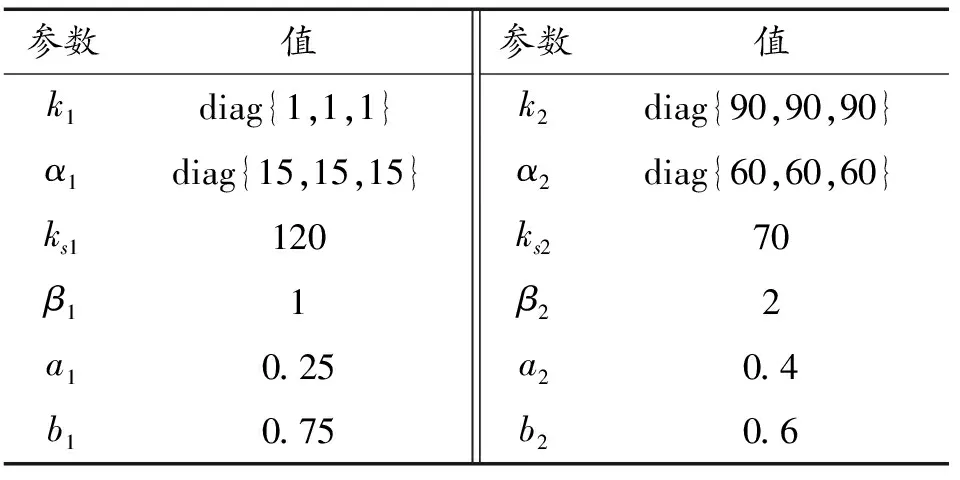
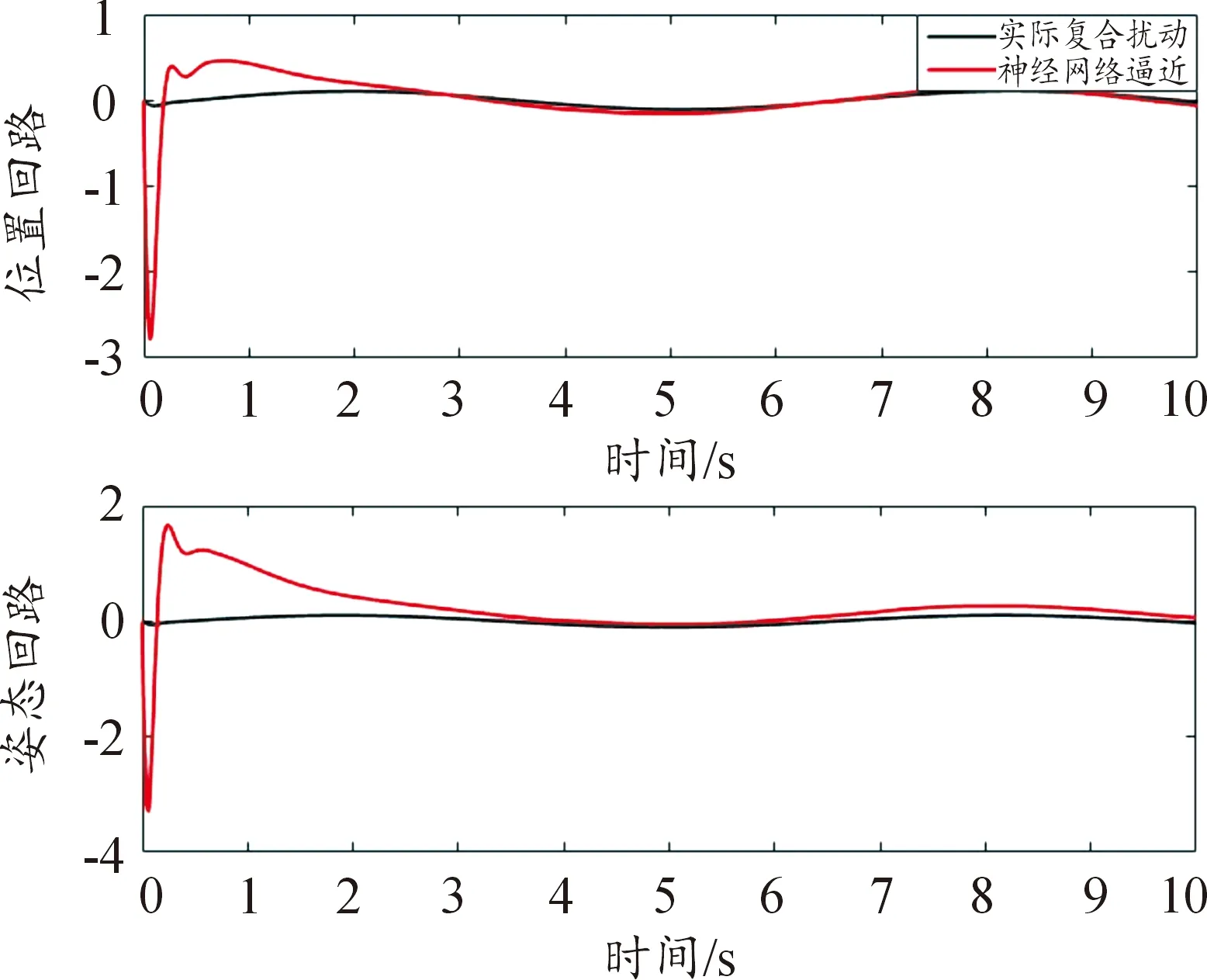
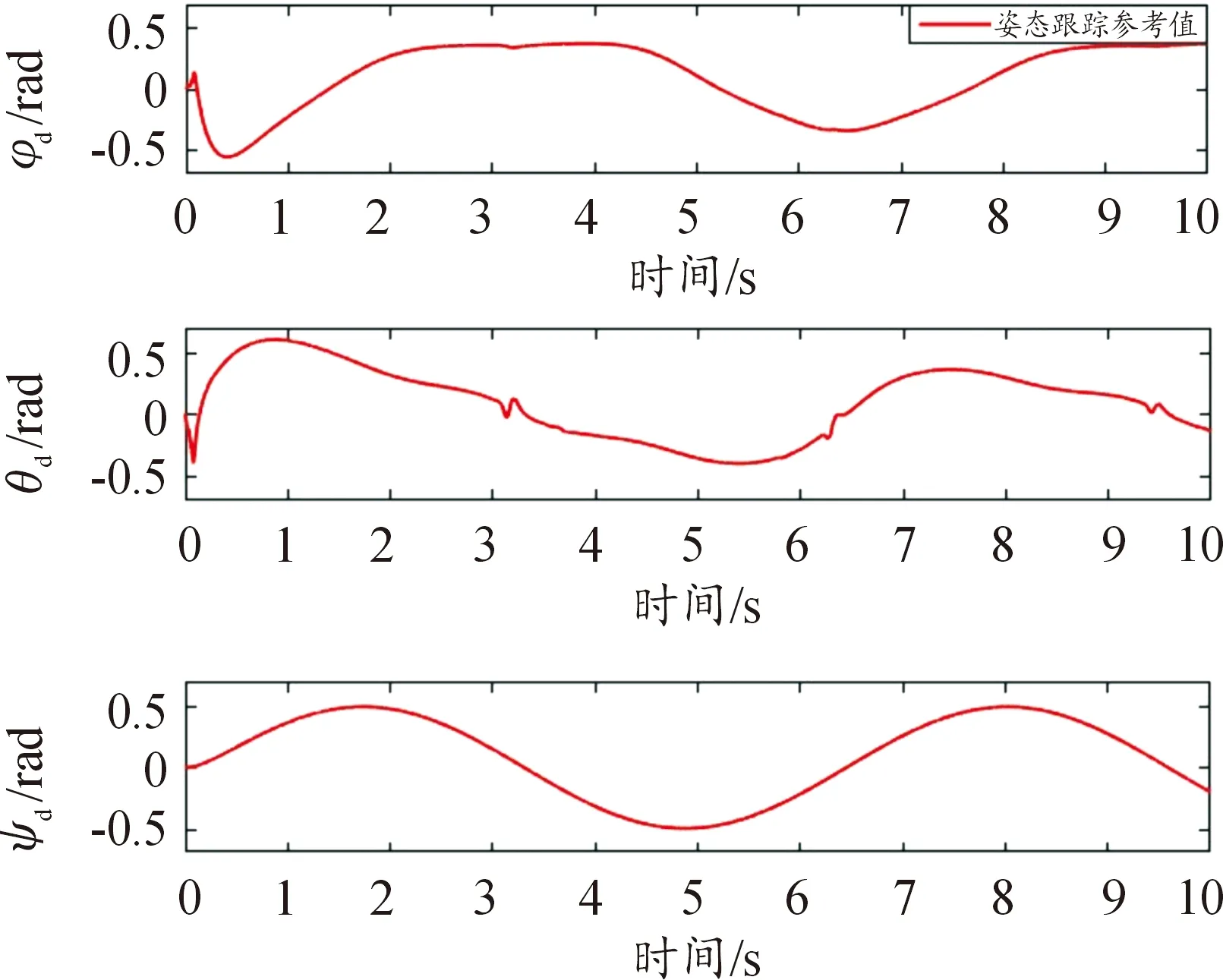
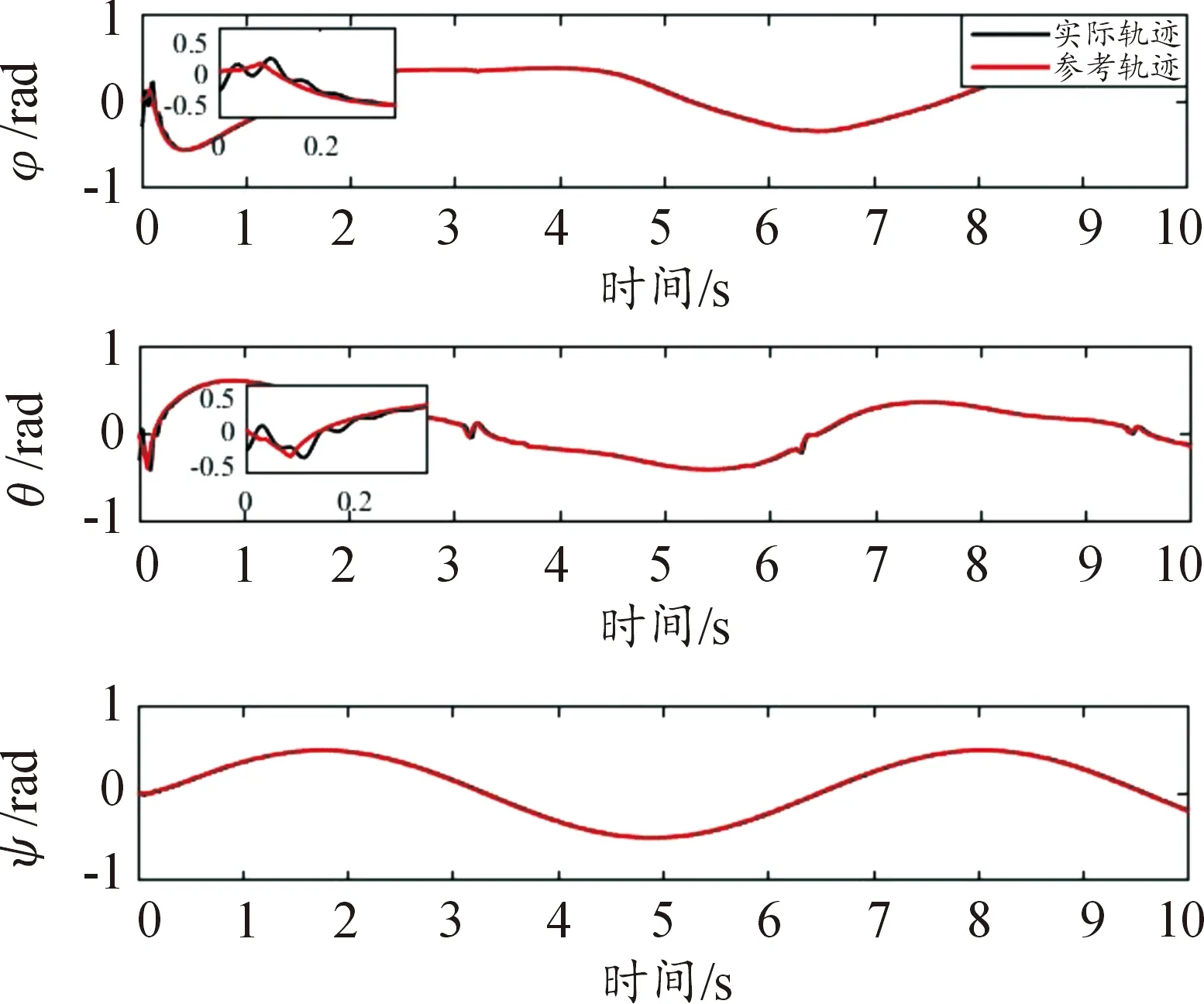
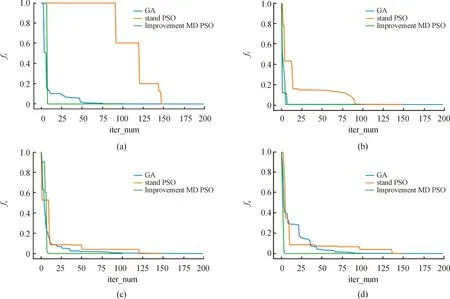
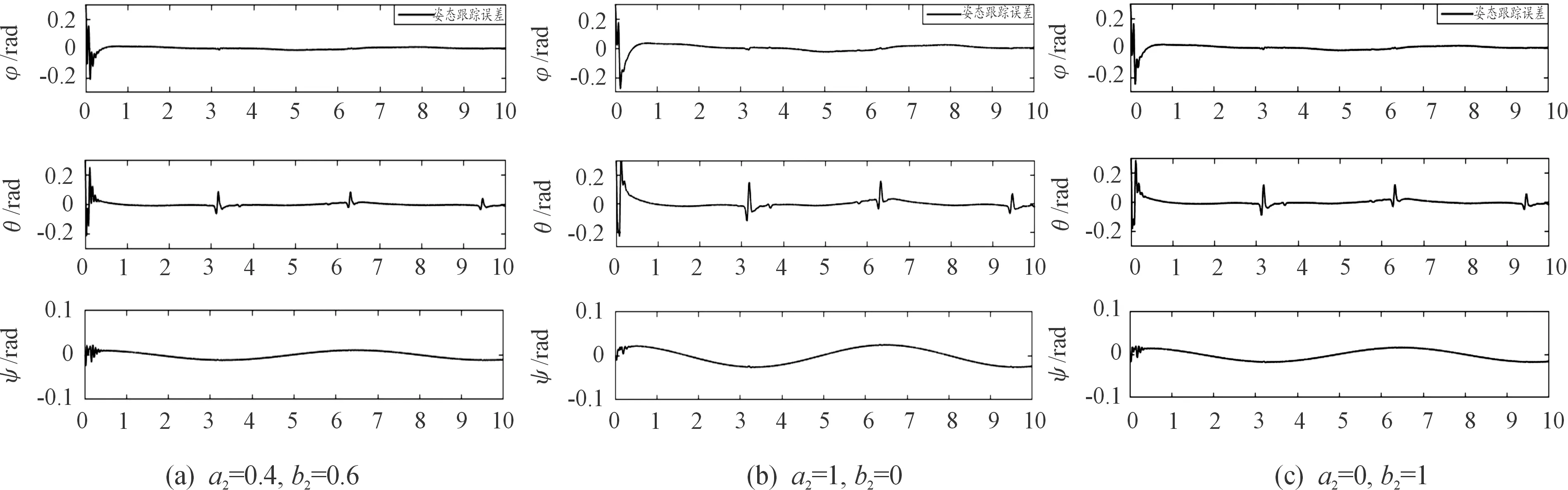
其中ks1和β1是待設計的正定控制參數,z2(0)是濾波誤差初始值,0 備注4式(22)中控制器設計,當a1=0時,RISE控制器僅以r1作為輸入信號,當b1=0時,控制器則以z2作為輸入信號,因此與文獻[11-12]相比,本文中設計策略能兼顧上述2種方法優點,有助于獲得更好的跟蹤控制效果。 綜合式(21)和式(22),位置回路控制器的整體控制律設計如下: β1(a1sgn(z2(τ))+b1sgn(r1(τ)))]dτ+ (23) 將式(18)、式(19)及式(23)代入式(17),可得到位置跟蹤誤差閉環動力學滿足: ε1-ε2-u1r (24) (27) 接下來,定義輔助函數分別如下: 則式(27)中位置跟蹤誤差閉環系統最終改寫為 本小節主要目標是設計姿態回路設計控制律u2,從而獲得姿態跟蹤誤差閉環系統。根據式(4)將內環姿態動力學系統描述為 (33) 其中記A2=HF2(x2),B2=HG2(x4)為對應姿態控制輸入u2的參數矩陣,Δ2=[Δf2(x4)+d2(t)]為系統模型不確定性和外部干擾組成的復合擾動。 姿態回路中偏航角參考信號ψd為提前設定,而俯仰角參考信號θd和滾轉角參考信號φd由位置控制器輸出變換得到。將式(23)中位置控制輸出u1改寫為u1=[ux,uy,uz]T,則θd、φd和Tm可由下式分別表示[25]: (34) (35) 定義姿態信號跟蹤誤差為 z3=x3d-x3 (37) 則姿態回路的濾波跟蹤誤差: 其中,k2和α2是待設計的正定濾波增益矩陣。將式(32)、式(33)和式(37)代入式(38)可得到: 定義2個輔助函數分別如下: 根據引理2,利用RBFNN對D(χ2)和Δ2進行逼近,并表示為 姿態控制器同樣分2部分設計,而控制器中涉及NN部分的控制律設計如下: 而基于RISE方法設計控制律時,同樣改進文獻[11-12]的設計方法,將zz4和r2均作為符號函數的輸入并引入權重重新組合,即: u2r=(ks2+1)z4-(ks2+1)z4(0)+ β2[a2sgn(z4(τ))+b2sgn(r2(τ))]}dτ (46) 其中,ks2和β2是待設計的正定控制參數,z4(0)是濾波誤差初始值,0 (47) 進而將式(42)、式(43)和式(47)代入式(41),可得到姿態跟蹤誤差動力學滿足: ε3-ε4-u2r (48) (49) (51) 定義輔助函數分別如下: 則式(51)中姿態跟蹤誤差閉環系統最終改寫為 上節針對給定的參考信號x1d=[xd,yd,zd]T和ψd,基于式(23)和式(47)中所設計的控制律,分別獲得了位置跟蹤誤差閉環系統式(31)和姿態跟蹤誤差閉環系統式(55),本節將借助Lyapunov穩定性理論分析整合后閉環系統的穩定性。為了簡化分析過程,下面首先給出信號邊界性定義和證明所需引理。 其中ρ1和ρ2具有全局性。 同時,根據引理2,可得到N1d和N2d以及它們導函數均有界[25],即: 式(57)、式(58)中ξNb1,ξNb2,ξNb3,ξNb4,ξNd1,ξNd2,ξNd3和ξNd4均為正常數。 引理3[26]定義輔助函數M如下: 如果式(59)中控制器增益β1滿足以下條件: 則函數: 滿足正定性。 證明:針對輔助函數M(·)積分: (62) (63) 針對式(63)中進一步處理,可得: 則N>0成立,即引理3得證。 則函數Q: 也滿足正定性。 綜上所述,為了分析整合后跟蹤誤差閉環系統穩定性,將上述設計過程總結為如下定理。 定理1考慮具有模型不確定性和外部干擾的UAH系統(4)滿足假設1—假設3,針對復合干擾Δ1,Δ2分別利用RBFNN技術對式(19)和式(43)進行估計,基于式(21)和式(45)中RBFNN控制器,式(20)和式(44)中估計權重值在線更新律以及式(22)和式(46)中改進RISE控制器,設計式(23)中位置回路控制律和式(47)中姿態回路控制律,如果式(60)和式(65)中條件滿足,則跟蹤誤差閉環系統有界穩定,即跟蹤誤差z1和z3隨時間漸近收斂至足夠小界限內。 證明:選取Lyapunov函數如下: (67) 綜合利用式(13)、式(14)、式(31)、式(37)、式(38)、式(55)、式(61)和式(66),則V導函數求得如下: (68) 根據楊氏不等式放大,可得到關于z1,z2,z3,z4的不等式如下: 將式(56)和式(69)代入式(68),得到: (70) 如果選取控制器增益ks1,ks2滿足以下條件: 從而進一步定義區間D為: 本節將在Matlab/Simulink環境下進行數值仿真,驗證本文中所提軌跡跟蹤控制方案的有效性。 根據文獻[4],UAH系統詳細參數列于表1中。假設初始狀態為x0=-2 m,y0=2 m,z0=2 m,為了更好說明,參考跟蹤軌跡設置為包含能量有界測量噪聲的情形: 表1 測試函數及其相關屬性 表1 UAH系統各項參數Table 1 Parameters of UAH system (75) 而滾轉角參考信號φd和俯仰角參考信號θd分別根據式(34)和式(35)計算得出。仿真中,UAH位置子系統外部干擾均為0.1sin(t)N,姿態子系統外部干擾均為0.1sin(t)N,而受到的不確定性項設置為與狀態相關的向量,分別如下:: 針對非線性UAH系統模型設計的位置控制律和姿態控制律分別為式(23)和式(47),控制參數選取如表2所示。控制器中RBFNN部分參數選取為:高斯函數寬度d1=0.5,d2=0.5,d3=0.5,d4=0.5,權重更新律的學習增益矩陣Γ1=5,Γ2=20,Γ3=5,Γ4=25。 表2 測試函數運行結果 表2 控制器主要參數設計 圖2顯示UAH系統復合擾動的估計過程,可見最終估計值和實際值的偏差收斂至可接受界限內。圖3說明了位置軌跡跟蹤過程,黑色曲線為UAH實際位置軌跡,而紅色曲線為式(75)定義的UAH參考軌跡,可看出由于存在測量噪聲的影響,參考軌跡與預先設定的軌跡存在一定的偏差。此外,由于UAH初始位置不在參考軌跡上,因此起始階段跟蹤軌跡存在較大誤差,但仍可在3 s內快速跟蹤參考信號,即跟蹤誤差趨于零,由此可見雖然存在測量噪聲影響,位置控制器依舊能使UAH有效跟蹤給定的軌跡。圖4展示了位置控制輸出轉換生成滾轉角φ、俯仰角θ的參考信號和式(75)給出偏航角ψ的參考信號,可得出由位置回路控制輸出產生的參考姿態角φd和θd均在合理的范圍內。需要指出的是,同樣在生成軌跡前期,會存在少量信號的振蕩。 圖2 全局尋優流程 圖2 RBFNN逼近復合擾動結果 圖3 位置跟蹤結果 圖3 位置更新策略 圖4 姿態參考軌跡 圖4 函數f1-f4進化曲線 圖5顯示了姿態跟蹤過程,黑色曲線為UAH實際姿態角軌跡,而紅色曲線為參考軌跡,可以看出偏航角ψ能夠快速跟蹤上參考軌跡,而滾轉角φ和俯仰角θ在經歷初始時刻的信號振蕩導致的較大跟蹤誤差后,同樣也可以迅速跟蹤參考信號。這里振蕩原因在于剛開始跟蹤時,輸入信號不夠充分,RBFNN不能對UAH模型不確定性和外部干擾組成的復合擾動進行準確估計。最后,可見姿態角同樣具有良好的跟蹤效果,跟蹤誤差均處于足夠小的界限內。同時,為了驗證本文中所提控制方法有效性,通過將本文中所提方法對比文獻[11]和文獻[12]中所使用的方法,分別仿真實驗對比,結果如圖6所示。 圖5 姿態跟蹤結果 圖5 函數f5-f8進化曲線 圖6 第一、二架無人機風險收益(f1),路徑收益(f2)和毀傷程度(f3)的變化 圖6 姿態軌跡跟蹤誤差結果對比 圖7 第三、四架無人機風險收益(f1),路徑收益(f2)和毀傷程度(f3)的變化 圖6(a)為本文中所提控制方法,即使用跟蹤誤差濾波信號及其變化率權重組合作為RISE輸入,以姿態回路為例,選擇權重值a2=0.4,b2=0.6;圖6(b)為文獻[11]中所提控制方法,即僅使用誤差濾波信號作為RISE輸入信號,即a2=1,b2=0;圖6(c)為文獻[12]中所提控制方法,僅使用誤差濾波信號變化率作為RISE輸入信號,即a2=0,b2=1。對比可見圖6(b)的姿態軌跡跟蹤誤差在三者中最大,從3、6.3和9.5 s時偏航角的跟蹤誤差可明顯體現出來。而且,分別從三個姿態角來看,圖6(a)曲線均趨于水平,也可以說明其軌跡跟蹤誤差最小。此外,圖6(a)前期跟蹤誤差振幅最小,均低于0.2 rad且收斂速度最快,而圖6(b)前期跟蹤誤差波動幅度最大,甚至超出0.3 rad且收斂速度最慢,圖6(c)則介于兩者之間。 綜合以上仿真分析可知,本文中所提出的UAH軌跡跟蹤控制方案不僅有效而且具有優越性。 本文中建立了將RBFNN和改進RISE結合的UAH控制設計方案,對于存在模型不確定性和外部擾動的非線性UAH系統,能夠準確跟蹤參考軌跡。主要結論如下: 1) 針對存在模型不確定性和外部干擾的UAH非線性系統,綜合利用RBFNN和改進后的RISE控制技術,以跟蹤誤差信號作為RBFNN輸入估計由模型不確定性和外部干擾構成的復合擾動,提高干擾估計的精度和速度。同時,以跟蹤誤差濾波信號及其變化率權重組合作為RISE輸入,在減少算法對UAH動力學模型依賴程度的基礎上,依舊獲得較好的跟蹤控制效果。 2) 使用更新律對RBFNN控制器在線訓練權重,相對離線設置權重的方式更為便捷。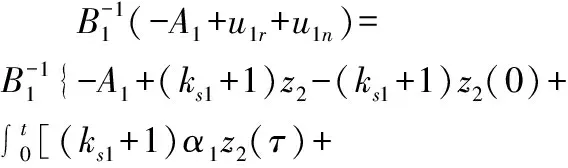
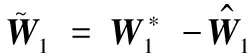
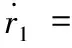
2.2 姿態系統跟蹤控制
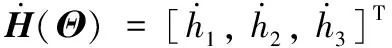
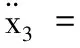
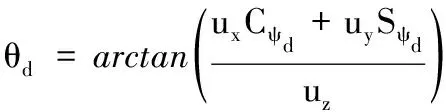
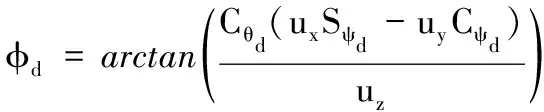
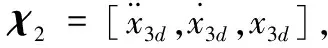
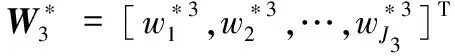
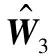
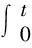
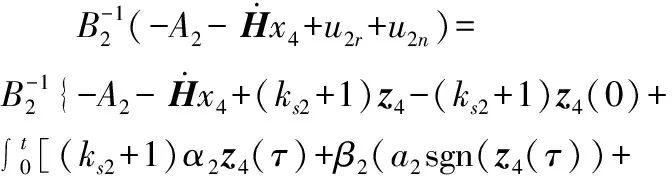
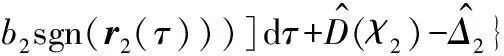
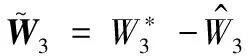
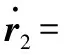
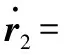
3 跟蹤誤差閉環系統穩定性分析
3.1 預備知識與引理
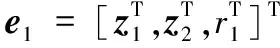
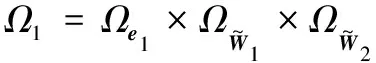
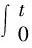
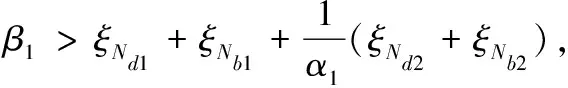
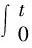
3.2 閉環系統穩定性準則
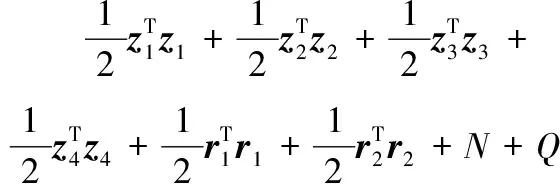
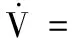
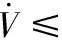
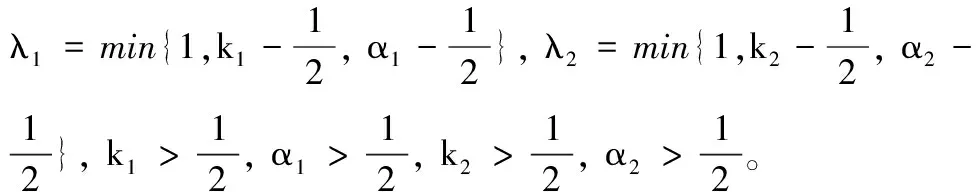
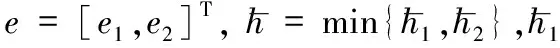
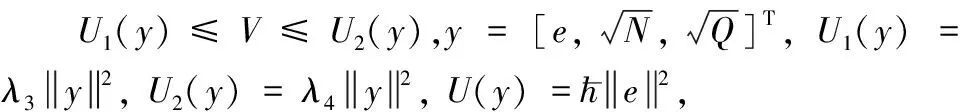
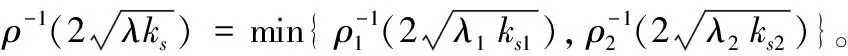
4 仿真結果及分析


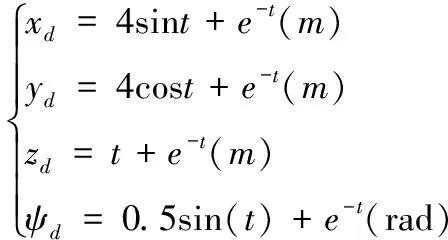

5 結論

