面向機械方向學科融合的數值分析課程教學改革與實踐

胡永旭

摘 要：數值分析課程是高等院校機械類專業的公共類課程或專業選修類課程，提高數值分析課程教學質量有助于幫助學生獲取利用數值計算方法解決工程實際問題的能力。針對數值分析課程與機械類專業課程融合不足的問題進行了探討，論述了以解決機械學科專業問題為導向，以數學軟件為工具，以機械學科專業知識融合為教學目的的數值分析課程教學改革的多項舉措。以理論力學和汽車試驗技術為例講解了面向機械專業的數值分析課程教學改革方法，以支持向量機的求解問題講解了數值分析課程如何與學科前沿理論知識結合。最后倡導了以學科融合為主，通過動畫展示和引入學科前沿知識激發學生學習數值分析興趣的教學理念。

關鍵詞：數值分析 學科融合 教學改革 動畫教學

Teaching reform and practice of numerical analysis course for integration of mechanical disciplines

Hu Yongxu

Abstract：The course of numerical analysis is a public course or a professional elective course of engineering subject in colleges and universities， improving the teaching quality of numerical analysis course is helpful to help students acquire the ability to solve practical engineering problems by using numerical calculation method. This paper discusses the integration of numerical analysis course and other professional courses， and discusses several measures of numerical analysis course teaching reform which is oriented to solve the professional problems of related disciplines， takes mathematical software as the tool， and takes disciplinary integration as the purpose of teaching. Taking theoretical mechanics and automobile test technology as examples， the teaching reform method of numerical analysis course for mechanical specialty was explained， the purpose of introducing frontier theory knowledge is explained by solving the problem of support vector machine. Finally， it advocates the teaching concept of integrating disciplines， stimulating students' interest in learning numerical analysis through animation display and introducing frontier knowledge of disciplines.

Key words：Numerical analysis; Integration of disciplines; Teaching reform; Teaching of animation

1 引言

數值分析課程是高等院校機械專業的公共類課程或專業選修類課程，該課程著重于鍛煉學生將復雜非線性數學問題轉換為簡單線性數學問題的能力，并要求學生能夠利用迭代或近似方法對問題進行求解。同時，數值分析課程也是培養學生實踐能力的一門課程，完成數值分析課程的學習后，學生應當能夠用數學語言描述機械專業的復雜問題，并且能夠構造數值計算算法和利用計算機軟件進行問題的求解。但傳統數值分析課程的教學一般僅針對數值求解問題本身，而未與機械專業中的其他課程產生聯系，導致學生無法使用數值分析工具解決機械專業的實際工程問題。將各專業學科進行交叉融合，使大學教育形成一個有機整體一直是教育者們關注的問題，各研究者也提出了很多相關的教育理念[1，2]，但數值分析課程與機械學科專業知識的學科融合教學改革研究稍顯不足。

2 數值分析課程的特點及教學中的不足

數值分析課程主要包含了插值計算，擬合分析，數值積分與微分，非線性與線性方程組求解，常微分方程初值問題的數值解法等內容，其特點是：（1）公式推導較多，推導過程較復雜且需要一定抽象思維；（2）算法構建基于近似和等效，將非線性復雜問題轉化為了線性問題；（3）算法便于在計算機上編程實現。這些特點決定了數值分析是一門知識豐富、理論抽象、實踐性非常強的課程。

但是從現狀來看，數值分析課程教學存在以下方面的問題：（1）教學內容仍偏重于理論。受到課時數的限制，數值分析課程一般都將教學重點放在數值計算的理論講解方面，應用數值分析理論進行建模和求解的實踐教學課時較少，其結果是學生僅僅初步了解了數值計算的理論原理，但沒有通過深入實踐學會如何提出問題和解決問題。2）理論教學沒有和機械專業其他課程的理論知識融合，無法形成學科體系。對于機械專業學生來說，數值計算算法是解決本學科專業問題的有利工具，數值計算方法和專業中的其他理論問題存在著天然聯系，但是目前針對數值計算的教學沒有能夠將機械專業課程的理論知識融入到教學內容中，使得數值分析課程的教學內容空洞且沒有著力點。3）實踐課題與現實工程問題聯系不緊密，探討問題過于數學模型化。數值分析針對的問題是實際工程中所面對的問題，但是目前課程教學實踐的內容仍是基于一般數學問題（方程，方程組，微分方程，積分求解等），沒有將實際工程問題與數值求解方法結合起來，導致實踐內容無法激起學生學習的興趣，實踐效果較差。

對于數值分析課程目前存在的一些問題和不足，許多教育工作者提出了解決方法并進行了方法實踐，如以數學建模為實踐內容進行數值分析課程教學改革，加強理論教學與實踐教學的聯系，或在教學過程中加入數學史的介紹，讓學生了解學科的發展過程等[3-6]。

3 以學科融合問題為導向構筑理論教學內容

從數值分析課程的特點來看，擬合分析與機械材料的疲勞曲線解析表達存在一定聯系，常微分方程數值問題與機械專業的力學相關課程和專業知識聯系較緊密，其他章節課程也都和學科中其他課程的專業理論知識存在一定關聯，因此可以以學科融合問題為導向構筑理論教學內容。

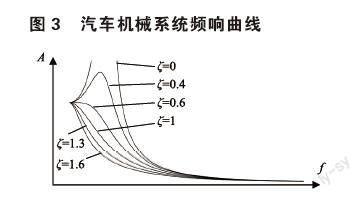
以汽車外形設計為例，如圖1所示，當汽車外形的關鍵點的尺寸[（x1，y1），…， （x1，y1）]確定后，其余位置的汽車外形輪廓點坐標可以用三次樣條插值方法進行計算，得到的設計輪廓具有過渡平滑，流線型強的特點，可以輔助工程師進行汽車輪廓設計。此外，擬合方法可以幫助學生以函數形式理解主尺寸選用的原則；非線性方程組求解方法可應用于優化問題；微分方程的初值問題可以用于求解理論力學中的動力學問題等。

學科融合的根本目的在于加強學生對機械專業知識的理解，起到溫故而知新的作用，同時為后續課程的學習提供平臺。由于學科融合的本質是鍛煉大學生的知識綜合運用能力，因此學科融合后的教學內容既有利于學生對數值分析知識的理解，又有利于機械專業的學生加強對專業理論知識的掌握，非常全面，起到了綜合訓練的作用。大學生的專業課程和未來的工作內容有著緊密聯系，具有很強的現實意義，因此面向多學科融合的數值分析課程能夠幫助學生在未來更好解決實際工作問題。將數值分析教學內容與機械專業的其他理論緊密結合也為學生的仿真分析學習提供了有力的平臺，實現了教學和科研的良性互動，促進了教學和實踐的聯系。

4 將求解過程用動畫展示，幫助學生理解，提高學生興趣

以往數值分析計算的求解結果都是以曲線或圖表進行展示，該種方法有利于學生理解結果和算法之間的內在聯系，卻不利于提高學生對工程問題解決方案的感性認識。例如多連桿機構的尺寸設計是機械專業理論力學課程的基本教學內容，專業課主要是教學生如何使用解析方法求解各連桿的尺寸，但是由于缺少動畫展示，學生對確定尺寸后的多連桿機構運動特性沒有感性認識。

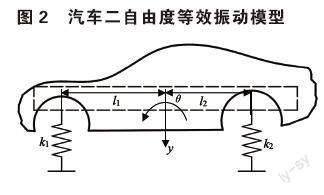
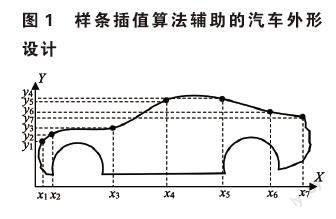
在汽車試驗技術這門課中，教材用車身動力學頻響曲線（如圖3所示）解釋車身的共振區間以及不同頻率激勵力下的車身振動特征，但是學生無法通過教材真實感受到不同頻率激勵力作用下汽車的振動位移，教學效果較差。如圖2所示，汽車的垂向振動特性和俯仰振動特性可以用彈簧-質量等效動力學模型進行描述，描述微分方程為式（1）。

式中：k1為前懸架剛度，k2為后懸架剛度，M為車身質量，J為車身俯仰轉動慣量，l1為前懸掛到汽車車身質心的距離，l2為后懸掛到汽車車身質心的距離，z為車身垂直運動距離，θ為車身俯仰角度，Fz為是的車身發生垂向運動的作用力，Mθ為使車身發生俯仰運動的作用力矩。在給定輸入條件下，微分方程（1）可以應用數值計算中的歐拉法，梯形公式，龍格庫塔法等算法求解。在使用數值方法進行求解時，輸入激勵力和力矩的頻率可以設置為如式（2）所示的連續變化，這樣既可以幫助學生理解用掃頻法獲取系統函數的原理，又可以通過動畫演示不同激勵頻率下車身的振動幅度讓學生對汽車的共振有更深刻的理解。

現在很多的數學軟件（MATLAB， Maple等）都具有制作動畫的功能，借助動畫縮放功能，學生能夠直觀感受地到車身的微幅振動的變化，更有利于學生理解頻響曲線與實際車身振動的聯系。除了能更好地幫助學生理解機械專業的知識以外，制作動畫的過程還極大地鍛煉了學生的編程能力。動畫制作訓練了學生的程序規劃，函數調用，程序調試等技能，對于學生掌握計算機編程語言，學會用計算機程序實現數值分析算法十分有益。

5 引入學科前沿理論知識，深化學科認識

課程教學內容的更新和改革已成為大學教學改革的一項重要內容，但總體上看數值分析課程教學內容的更新速度滯后于機械學科前沿成果的發展速度，沒有將最新的機械學科理論知識與數值算法緊密結合起來。目前數值分析算法已經成為機械領域設計、材料、故障診斷等問題求解的必要手段，如有限元分析，動力學分析，人工智能的計算問題都與數值算法息息相關。例如在人工智能領域，支持向量機技術已經成為解決分類決策問題的一種重要方法，支持向量機的數學公式表述可以是不等式條件下的條件極值問題，即：

式中：γ為樣本點到分類超平面的距離，y為樣本的決策屬性值，為±1，w為分類超平面的系數，是一個n維的向量，b是分類超平面的參數標量。引入拉格朗日乘數后，式（3）的函數表達式為：

對于僅含等式約束的條件極值問題，可以直接由式（4）對各變量求偏導數獲得問題的解，但是對于含有不等式約束的條件極值問題，則必須用KKT條件將條件極值問題轉化為無條件極值問題再進行求解。引入KKT條件后，式（4）的求解方程為：

關于式（5）的求解，當問題的維度較低或樣本數量較少時，可以用牛頓迭代法，但是當樣本較多或維度較高時，需要將式（4）化為對偶問題，再利用KKT條件求解。化為對偶問題后，式（4）的求解方程為：

目前數值分析課程中的求解方法已經不能滿足式（6）的快速求解，而必須使用啟發式（SMO）算法進行求解。啟發式 算法由微軟研究院提出，是目前運行速度最快的二次規劃優化算法，特別適合線性支持向量機模型的學習或數據稀疏場景。教師通過講解支持向量機問題可以引入新的數值求解方法，通過對新的數值求解方法的講解有利于為學生拓寬數值計算和計算機方面的知識，深化對人工智能的理解和認識。

通過將機械專業前言理論知識與數值分析課程教學內容進行融合可以極大地拓寬學生的科學視野，有利于培養學生的創新意識，更有助于學生未來的發展。因此，教師可以基于自己的學術研究領域，在教學中通過實例講解適當地將一些新的機械專業成果和實踐經驗貫徹到課堂教學和實踐中，這既保證了教學內容與學科前沿的緊密結合性，又提高了學生的學習興趣。

6 結語

作為數學理論和計算機科學結合的產物，數值分析算法和學科專業知識存在著緊密的聯系。針對目前數值分析課程存在的與機械專業知識聯系不緊密，結果展示方法單一，教學內容滯后于機械學科前沿理論的問題進行教學改革是必要的。面向多學科融合的數值分析課程教學改革與實踐的目的是增強數值分析課程與機械專業課程的聯系，借助數值計算課程將機械專業大學課程形成統一的整體，達到優化教學過程，提升教學質量，實現教師與學生良好互動的目的。

參考文獻：

[1]魏朋，楊紅英，張一風，等. 多學科交叉融合工程人才培養模式探索與實踐——以非織造材料與工程專業為例[J]. 高分子通報，2022（3）：7.

[2]張戎，劉新建，許寧，等. 多學科協同教學的應用初探——以“人獸共患病學”教學為例[J]. 教育教學論壇，2022（30）：5.

[3]劉艷偉，司軍輝. 數值分析課程教學改革若干問題探討[J]. 黑龍江教育學院學報，2010（6）：2.

[4]沈海龍，邵新慧，宋叔尼. 數值分析課程教學改革的探索與實踐[J]. 大學數學，2013（5）：1-3.

[5]袁海燕，宋成.應用型人才培養模式下《數值分析》教學改革的幾點探討[J]. 學理論，2012（3）：2.

[6]覃桂茳，涂井先，許成章，等. 翻轉課堂教學模式在數值分析課程教學改革中的研究與實踐[J]. 黑龍江科學，2022（009）：013.