數(shù)學(xué)問題設(shè)計(jì)的誤區(qū)和出路

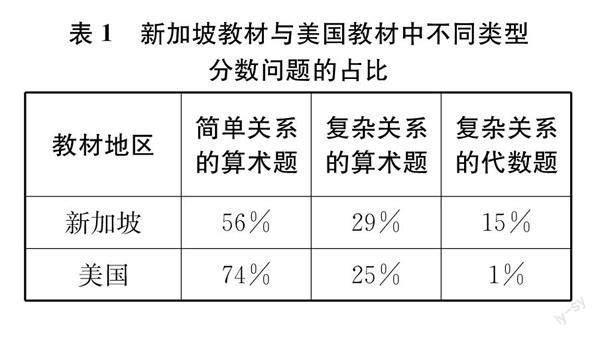
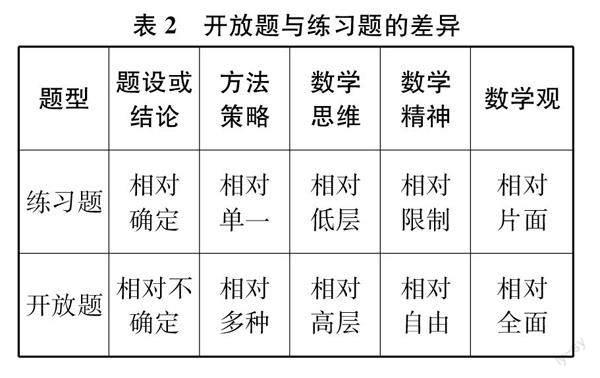
摘要：數(shù)學(xué)問題可以分為回憶型、連接型、反省型三類。一味重視練習(xí)題（回憶型問題），使得過程思維的發(fā)展空間狹窄。開放題（反省型問題）的出現(xiàn)，旨在平衡內(nèi)容知識(shí)與過程思維。但是，開放題在進(jìn)入日常教學(xué)時(shí)，遭遇了一些障礙。對(duì)此，應(yīng)該重視連接型問題組的設(shè)計(jì)，將其作為課程載體，促進(jìn)從基礎(chǔ)知識(shí)到高層次思維的連續(xù)發(fā)展，促進(jìn)內(nèi)容與過程的平衡。

關(guān)鍵詞：數(shù)學(xué)問題；練習(xí)題；開放題；連接型問題組

近幾十年來，美國(guó)數(shù)學(xué)課程中，“問題解決”被調(diào)整為數(shù)學(xué)教育的過程目標(biāo)之一，而不再像以前一樣作為數(shù)學(xué)教育的“核心”。這與“問題解決”中將問題界定為不熟悉的問題有關(guān)：把不熟悉的問題絕對(duì)化，違背循序漸進(jìn)的原則，因?yàn)椋瑥氖煜さ膯栴}到不熟悉的問題需要過渡和連接；忽視人類學(xué)習(xí)的一般規(guī)律，畢竟，從熟悉的問題到不熟悉的問題的遷移學(xué)習(xí)扮演著重要的角色。此外，許多研究單單關(guān)注問題提出或思維，脫離知識(shí)。這樣的“問題解決”猶如離開水的魚，難以長(zhǎng)期發(fā)展。

一、數(shù)學(xué)問題的分類和角色

問題在數(shù)學(xué)課程中扮演非常重要的角色。簡(jiǎn)單來說，簡(jiǎn)單問題（通常意義上的練習(xí)）和例題類似，扮演記憶例題方法的角色，某種意義上，可以作為“雙基”的課程橋梁；難的問題需要思考探索，扮演思維的角色，某種意義上，可以作為高層次思維能力的課程載體。

PISA曾按照一個(gè)公民在日常生活中理解數(shù)學(xué)、作出判斷、使用和從事數(shù)學(xué)的能力評(píng)價(jià)學(xué)習(xí)者……