具有隨機擾動和不確定性的中立型耦合神經網絡有限時間同步*
王柯杰, 陳巧玉, 童東兵, 毛 琦
(上海工程技術大學 電子電氣工程學院, 上海 201620)
0 引 言
神經網絡是模仿神經元信息傳遞過程所構建出的一種數學模型,可以用來解決一些復雜的非線性問題.近年來,神經網絡已經被應用于生物信號檢測、價格預測、風險評估和故障診斷等許多領域.隨著研究的不斷深入,中立型神經網絡吸引了越來越多的關注.它是神經網絡的特殊形式,其時滯在系統現在的狀態和狀態的導數中同時存在,由此導致該類系統具有更加復雜的動態行為,也使得此類系統相較于一般時滯系統具有更好的普適性.像化學反應過程、渦輪噴氣發動機的轉動過程等都可以利用中立型時滯系統進行建模.通過設計新的Lyapunov泛函和提出新的分析技巧,文獻[1]研究了一類具有混合時滯的中立型耦合神經網絡的指數同步.文獻[2]利用M矩陣方法和隨機分析法,研究了具有Markov切換參數的中立型隨機神經網絡的自適應同步.基于Lyapunov穩定性理論和不等式技術,文獻[3]針對一類具有多時滯的中立型神經網絡,研究了其平衡點的存在性、唯一性和全局漸近穩定性.
同步是指復雜網絡中節點達到相同狀態的行為,它不僅是一種基本的自然現象,也是復雜網絡科學領域的重要研究方向之一.在過去的幾十年里,學者們進行了全面的研究,并取得了大量的成果.其中,有限時間同步由于其優異的暫態性能而受到越來越多的關注[4].文獻[5]利用M矩陣方法得到了具有Markov拓撲和分布脈沖效應的神經網絡有限時間同步判據.針對一類模糊中立型耦合Rayleigh系統,文獻[6]利用有限時間穩定性理論和不等式技術,給出了其有限時間同步判據.對于具有自適應狀態耦合的多權重復雜網絡,文獻[7]通過Lyapunov穩定性理論,設計出合適的控制器,使其達到有限時間同步和H∞同步.
在神經網絡中,不確定性和隨機擾動往往會造成不穩定或抖振,這些因素不利于神經網絡的實際應用.因此對不確定時滯系統的研究一直是控制理論研究中的難點和熱點問題之一.本文研究了具有不確定性和隨機擾動的中立型耦合神經網絡有限時間同步問題,所構建的系統模型與文獻[8-10]相比引入了不確定性和隨機擾動,更具實際意義.在Lyapunov穩定性理論的基礎上,結合不等式技術,推導出中立型耦合神經網絡有限時間同步準則.為了解決不確定性和隨機擾動造成的問題,本文構造了合適的狀態反饋控制器來保證主從系統實現有限時間同步.以Kronecker積形式給出有限時間同步判據,易于使用MATLAB工具箱來檢驗.
1 問 題 描 述
考慮一類具有時滯和不確定性及擾動的中立型神經網絡,其驅動系統設計如下:
d[xi(t)-Dxi(t-τ)]=[-(C+ΔC)xi(t)+(A+ΔA)f(xi(t))+
(B+ΔB)f(xi(t-τ))]dt,i=1,2,…,N,
(1)
其中,xi(t)=[xi1(t),…,xin(t)]T∈n代表第i個節點的狀態向量,D=diag[d1,…,dn]且|di|<1,C=diag[c1,…,cn]是正定對角矩陣,A∈n×n和B∈n×n分別為連接權矩陣和時滯連接權矩陣,f(·)是神經元激活函數且有界,τ代表所考慮的時滯,未知矩陣ΔC,ΔA,ΔB代表系統參數的不確定部分.
其響應系統為
(2)
其中,系統參數D,C,A,B,ΔC,ΔA,ΔB的定義與式(1)相同,yi(t)=[yi1(t),…,yin(t)]T∈n,ui(t)為響應網絡第i個節點的控制輸入,c代表耦合強度,Γ=diag[γ1,…,γn]為內耦合配置矩陣,σi:+×n×n→n是噪聲強度函數,ωi(t)=[ωi1(t),…,ωin(t)]T是定義在完備概率空間的標準Brown運動,G=(gij)N×N是外耦合轉置矩陣,滿足
將同步誤差信號定義為ei(t)=col{ei1(t),ei2(t),…,ein(t)}=yi(t)-xi(t).根據矩陣G的性質,可得到
(3)
其中
誤差系統的耦合結構如圖1所示.
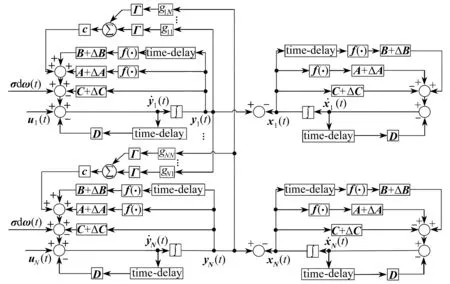
圖1 系統耦合結構圖Fig. 1 The coupling structure diagram for the error system
通過使用Kronecker積,可以將式(3)改寫為
d[e(t)-(IN?D)e(t-τ)]=
[-(IN?C)e(t)-(IN?ΔC)e(t)+(IN?A)F(e(t))+
(IN?ΔA)F(e(t))+(IN?B)F(e(t-τ))+(IN?ΔB)F(e(t-τ))+
(cG?Γ)e(t)+u(t)]dt+σ(t,e(t),e(t-τ))dω(t),
(4)
其中
σ(t,e(t),e(t-τ))=diag[σ1(t,e1(t),e1(t-τ)),…,σN(t,eN(t),eN(t-τ))].
誤差系統系統(4)中的控制器可以被設計如下:
u(t)=-R1e(t)+R2e(t-τ)-
ηsign(e(t)-(IN?D)e(t-τ))|e(t)-(IN?D)e(t-τ)|δ,
(5)
其中,對稱矩陣R1,R2∈nN×nN,η>0,sign(e(t)-(IN?D)e(t-τ))=diag[ei1(t)-d1ei1(t-τ),…,ein(t)-dnein(t-τ)]∈nN×nN,|e(t)-(IN?D)e(t-τ)|δ=(|ei1(t)-d1ei1(t-τ)|δ,…,|ein(t)-dnein(t-τ)|δ)T∈nN,0<δ<1,i=1,…,N.
為了得到主要成果,則以下假設、引理和定義需要被提供.
假設1 噪聲強度矩陣σ(·,·,·)是有界的,存在兩個已知矩陣M∈n×n,N∈n×n,滿足
tr(σT(t,e(t),e(t-τ))σ(t,e(t),e(t-τ)))≤eT(t)MTMe(t)+eT(t-τ)NTNe(t-τ).
假設2 神經元激活函數f(· )是有界的,且對于任意xij,yij∈,滿足下列條件:
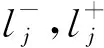
注1 在實際系統中,許多常用的神經元激活函數滿足假設2.例如Hopfield神經網絡[11]中常用的f(x)=1/(1+e-λx),f(x)=(1-e-λx)/(1+e-λx)(λ>0)和f(x)=tanh(x);細胞神經網絡[12]中常用的f(x)=(|x+1|-|x-1|)/2等.
假設3 未知矩陣ΔC,ΔA,ΔB滿足下列結構:
(ΔC,ΔA,ΔB)=PS(t)(H1,H2,H3),
(6)
其中P,H1,H2和H3是已知的實矩陣,不確定矩陣S(t)可以是時變不固定的,且滿足
ST(t)S(t)≤I.
(7)
注2 式(6)和(7)中的參數不確定性結構廣泛應用于不確定系統的隨機過程.式(7)可以對具有參數不確定性的實際系統進行精確建模.值得注意的是, 式(6)中的可變矩陣S(t)甚至可以是狀態相關的, 即只要滿足式(7),則S(t)=S(t,φ(t))成立.
引理1[13]存在x,y∈n,對任意ε>0,不等式xTy+yTx≤εxTx+ε-1yTy成立.
引理2[14]假設存在xi∈n,i=1,…n,0<ξ≤1,則下列不等式成立:
引理3[15]存在非負的連續函數χ(t)∈n,常數ζ∈(0,∞)和ξ∈(0,1)滿足
Lχ(t)≤-ζχξ(t),t∈n
則χ(t)的平凡零解在概率空間內是有限時間穩定的,且隨機設定時間滿足E{T0}≤χ1-ξ(0)/(ζ(1-ξ)).
定義1[16]假設存在任意常數T0∈(0,∞)滿足
則誤差系統(4)可以實現有限時間同步,其中t≥t0+T0,且T0為同步的設定時間.
2 主要定理及證明
在這一節中,我們將推導出主從系統實現有限時間同步的判據.
定理1 在假設1、2、3滿足的前提下,對于任意εi>0(i=1,2,…,10),對稱矩陣R1,R2滿足
(8)
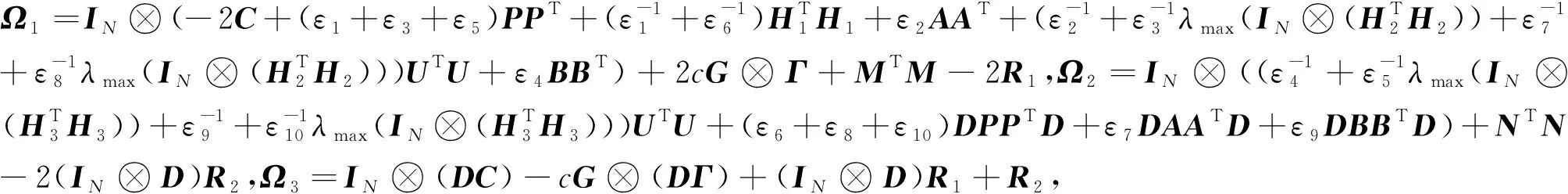
證明定義一個算子De(t)=e(t)-(IN?D)e(t-τ),并構造如下Lyapunov函數:
V(t)=(De(t))T(De(t)).
(9)
dV(t)=LV(t)+2(De(t))Tσ(t,e(t),e(t-τ))dω(t),
(10)
其中
LV(t)=2[(De(t))T[-(IN?C)e(t)-(IN?ΔC)e(t)+(IN?A)F(e(t))+
(IN?ΔA)F(e(t))+(IN?B)F(e(t-τ))+(IN?ΔB)F(e(t-τ))+
(cG?Γ)e(t)+u(t)]]+tr(σT(t,e(t),e(t-τ))σ(t,e(t),e(t-τ))).
(11)
根據假設1和假設3,將控制器(5)代入式(11),能夠獲得
LV(t)≤-2eT(t)(IN?C)e(t)-2eT(t)(IN?ΔC)e(t)+2eT(t)(IN?A)F(e(t))+
2eT(t)(IN?ΔA)F(e(t))+2eT(t)(IN?B)F(e(t-τ))+
2eT(t)(IN?ΔB)F(e(t-τ))+2eT(t)(cG?Γ)e(t)-2eT(t)R1e(t)+
2eT(t)R2e(t-τ)-2ηeT(t)sign(e(t)-(IN?D)e(t-τ))×
|e(t)-(IN?D)e(t-τ)|δ+2eT(t-τ)(IN?(DC))e(t)+
2eT(t-τ)(IN?(DΔC))e(t)-2eT(t-τ)(IN?(DA))F(e(t))-
2eT(t-τ)(IN?(DΔA))F(e(t))-2eT(t-τ)(IN?(DB))F(e(t-τ))-
2eT(t-τ)(IN?(DΔB))F(e(t-τ))-2eT(t-τ)(cG?(DΓ))e(t)+
2eT(t-τ)(IN?D)R1e(t)-2eT(t-τ)(IN?D)R2e(t-τ)+
2ηeT(t-τ)(IN?D)sign(e(t)-(IN?D)e(t-τ))|e(t)-(IN?D)e(t-τ)|δ+
eT(t)MTMe(t)+eT(t-τ)NTNe(t-τ).
(12)
根據假設2,可以得到
(13)
且
(14)
其中
由式(14),能夠獲得
eT(t)(IN?(UTU))e(t).
(15)
通過假設3和引理1,有
-2eT(t)(IN?ΔC)e(t)=
-2eT(t)(IN?(PS(t)H1))e(t)=
-2eT(t)(IN?P)(IN?(S(t)H1))e(t)≤
(16)
2eT(t)(IN?A)F(e(t))≤
(17)
2eT(t)(IN?ΔA)F(e(t))=
2eT(t)(IN?(PS(t)H2))F(e(t))=
2eT(t)(IN?P)(IN?(S(t)H2))F(e(t))≤
(18)
2eT(t)(IN?B)F(e(t-τ))≤
(19)
2eT(t)(IN?ΔB)F(e(t-τ))=
2eT(t)(IN?(PS(t)H3))F(e(t-τ))=
2eT(t)(IN?P)(IN?(S(t)H3))F(e(t-τ))≤
ε5eT(t)(IN?(PPT))e(t)+
(20)
2eT(t-τ)(IN?(DΔC))e(t)=
2eT(t-τ)(IN?(DPS(t)H1))e(t)=
2eT(t-τ)(IN?(DP))(IN?(S(t)H1))e(t)≤
(21)
-2eT(t-τ)(IN?(DA))F(e(t))≤
(22)
-2eT(t-τ)(IN?(DΔA))F(e(t))=
-2eT(t-τ)(IN?(DPS(t)H2))F(e(t))=
-2eT(t-τ)(IN?(DP))(IN?S(t)H2)F(e(t))≤
ε8eT(t-τ)(IN?(DPPTD))e(t-τ)+
(23)
-2eT(t-τ)(IN?(DB))F(e(t-τ))≤
(24)
-2eT(t-τ)(IN?(DΔB))F(e(t-τ))=
-2eT(t-τ)(IN?(DPS(t)H3))F(e(t-τ))=
-2eT(t-τ)(IN?(DP))(IN?(S(t)H3))F(e(t-τ))≤
ε10eT(t-τ)(IN?(DPPTD))e(t-τ)+
(25)
將式(16)—(25)代入式(12),可得
2cG?Γ+MTM-2R1]e(t)+2eT(t-τ)[IN?(DC)-
(ε6+ε8+ε10)DPPTD+ε7DAATD+ε9DBBTD)+NTN-
2(IN?D)R2]e(t-τ)-2η|e(t)-(IN?D)e(t-τ)|δ+1.
(26)
根據引理2,有
-2η|e(t)-(IN?D)e(t-τ)|δ+1=
-2η((De(t))T(De(t)))(δ+1)/2=
-2ηV(δ+1)/2(t).
(27)
接著對式(10)和(26)求數學期望,可得
(28)
其中
2cG?Γ+MTM-2R1,
(ε6+ε8+ε10)DPPTD+ε7DAATD+ε9DBBTD)+NTN-2(IN?D)R2,
Ω3=IN?(DC)-cG?(DΓ)+(IN?D)R1+R2.
當定理1成立時,E[dV(t)]≤-2ηE[V(t)](δ+1)/2.通過引理3,可以保證誤差系統(4)可以在設定時間T0=V(1-δ)/2(0)/(η(1-δ))實現有限時間同步,證明完成.
控制器算法的步驟如下:
步1 定義激活函數f(·)和Gauss函數的寬度σi,并選擇矩陣D,C,B,A,Γ,G;
步2 選擇不確定參數矩陣P,H1,H2,H3及噪聲強度矩陣M,N;
步3 通過e(t)=y(t)-x(t)計算e(t);
步4 選擇合適的參數η>0,0<δ<1,且由式(8)可以確定對稱矩陣R1,R2;
步5 計算u(t)的值,并將其用于產生控制信號.
3 仿 真
在本節中,我們將通過以下的仿真來檢驗所設計的反饋控制器的有效性.誤差系統(4)的參數設計為
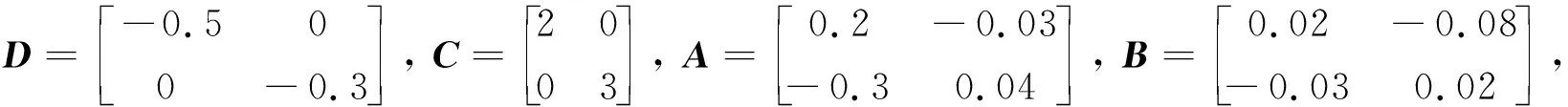
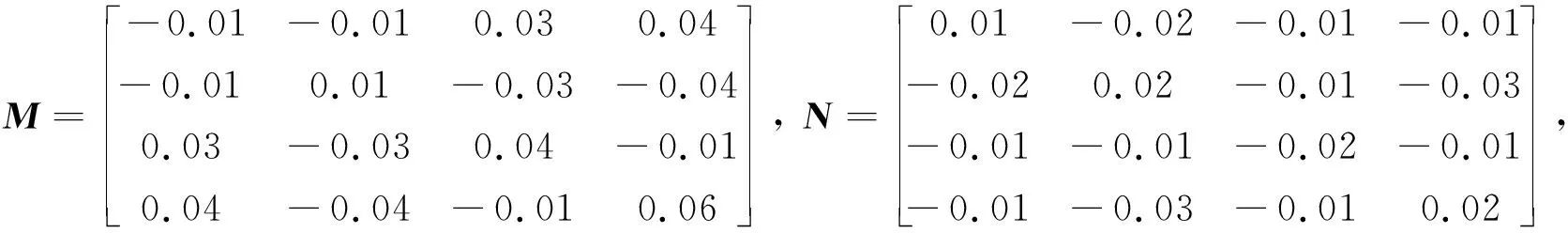
激活函數為f(·)=tanh(·),η=1.13,δ=0.5,x1(0)=[1.2,1.8]T,x2(0)=[1.5,0.8]T,y1(0)=[1.7,-2.3]T,y2(0)=[1.3,0.4]T,τ=0.1.通過使用MATLAB的Yalmip工具箱,求得
ε1=0.316,ε2=0.512,ε3=0.235,ε4=0.613,ε5=2.130,
ε6=0.718,ε7=0.223,ε8=0.313,ε9=0.524,ε10=0.413.
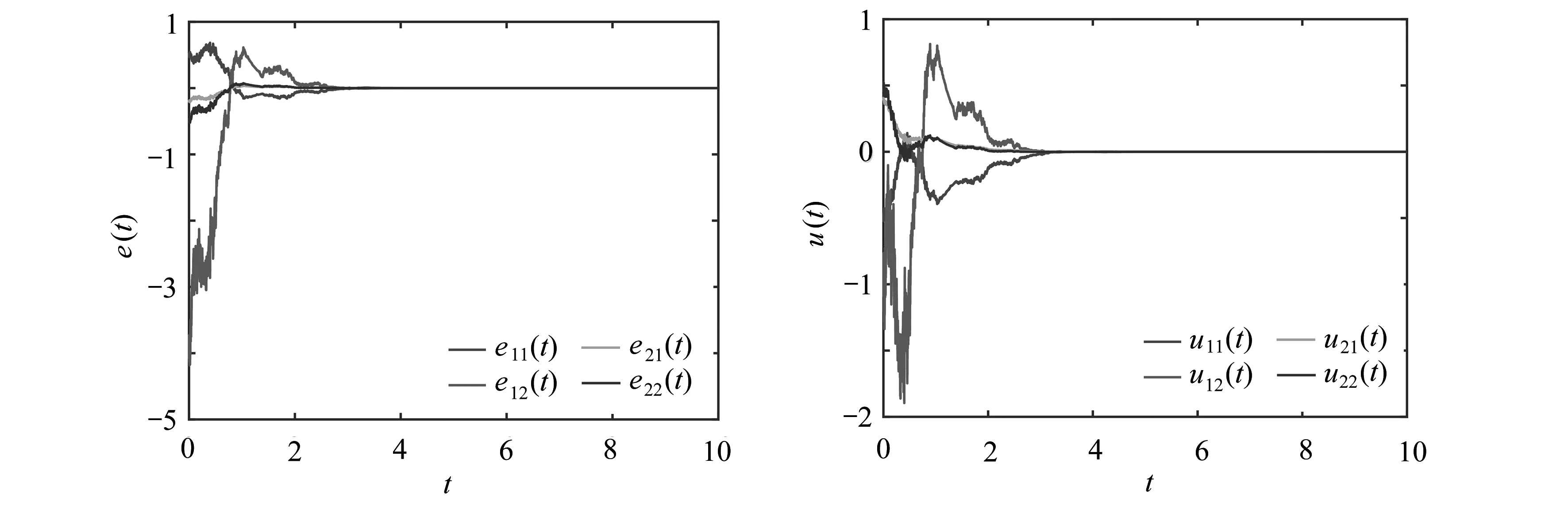
經過檢驗,以上結果滿足假設1、2、3和定理1中的條件.因此誤差系統(4)可以實現有限時間同步.通過仿真,可以得到以下仿真結果.圖2為隨機噪聲,圖3和圖4分別描繪了無控制輸入和控制器(5)作用下誤差系統(4)的狀態曲線,且同步時間t≈3.3 s 圖2 隨機噪聲 圖3 無控制器作用下的誤差系統狀態軌跡Fig. 2 Random noisesFig. 3 State trajectories of the error system 圖4 控制器(5)作用下的誤差系統狀態軌跡 圖5 控制輸入Fig. 4 State trajectories of the error system with controller (5) Fig. 5 Control inputs 注3 與文獻[17]的同步時間t≈5 s和文獻[18]的同步時間t≈10 s相比,本文所設計的控制器可以使系統在t≈3.3 s內達到同步,同步時間更短,更具優越性. 注為了解釋圖中的顏色,讀者可以參考本文的電子網頁版本. 本文進一步研究了中立型耦合神經網絡的有限時間同步問題.所使用的模型同時考慮了時滯、不確定性和隨機擾動的影響, 更具普遍性.通過構造合適的Lyapunov函數和運用不等式技術,推導出中立型耦合神經網絡的有限時間同步準則.設計適當的狀態反饋控制器,使所考慮的系統達到有限時間同步狀態.最后通過仿真結果檢驗了所獲結論的有效性.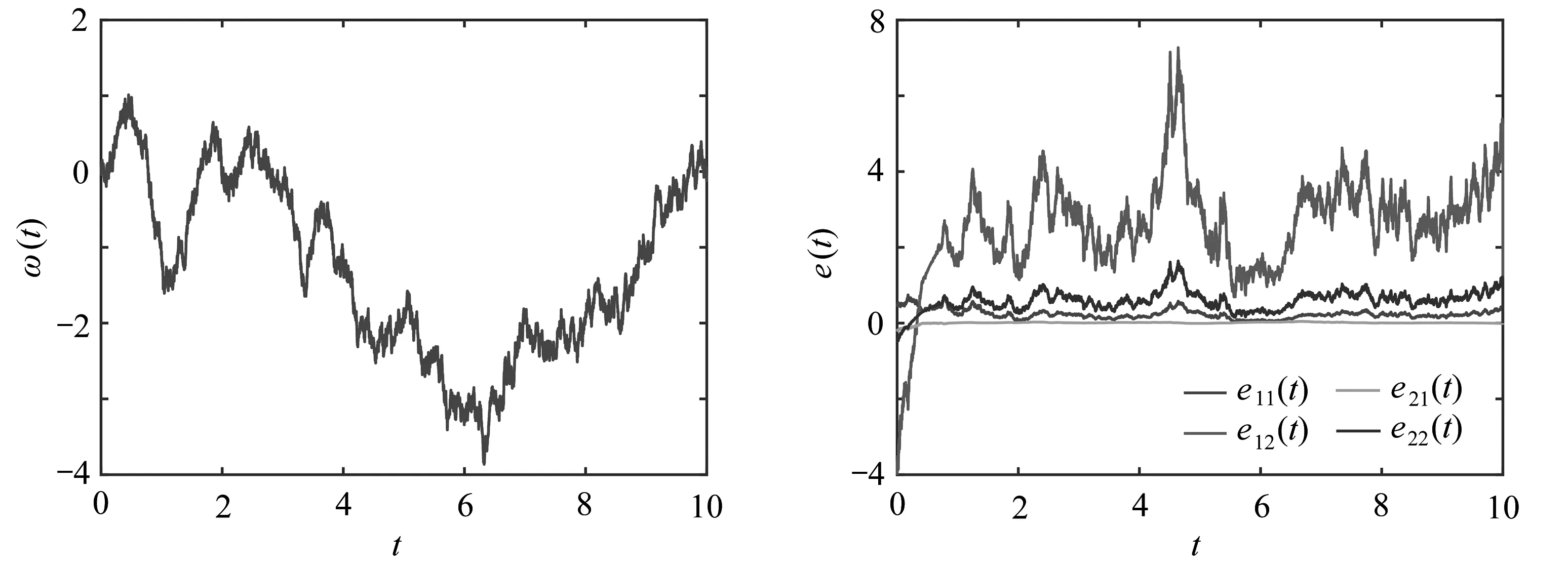
4 結 論

