基于輸出層具有噪聲的DQN的無人車路徑規劃*

李 楊, 閆冬梅, 劉 磊

(1. 河海大學 理學院, 南京 211100;2. 南京郵電大學 現代郵政學院, 南京 211100)

0 引 言

無人車是電子計算機等最新科技成果與現代汽車工業相結合的產物,是集環境感知、規劃決策、自主行駛等功能于一體的綜合系統,它集中運用計算機、現代傳感、信息融合、通訊、人工智能與自動控制等技術,是典型的高新技術綜合體．路徑規劃是無人車自主導航的重要前提,也是無人車完成其他各項任務的基礎．路徑規劃常采用A*算法[1]、遺傳算法[2]、蟻群算法[3]、人工勢場法[4]等,這些算法在無人車路徑規劃過程中都需要環境信息．強化學習方法[5-7]的出現以其獨特的運行過程和泛化性能解決了眾多問題,使得無人車進行路徑規劃時完全不需要環境信息,通過在訓練過程中不斷試錯,與環境進行交互,采用延遲回報的方式尋找最優動作以獲得最優決策能力[8],最終得到規劃路徑．

針對狀態數較少的離散狀態下的無人車路徑規劃,訓練一般選取Q-learning算法[9-12],主要通過改進Q-learning算法或修改獎勵函數提高算法訓練效率．但當狀態數較多時,使用此算法進行訓練會出現維度爆炸問題,訓練和收斂時間較長,成功率也較低．針對連續狀態下的無人車路徑規劃,Q-learning等表格型強化學習(reinforcement learning,RL)算法無法勝任,鑒于神經網絡有極強的表達能力[13-14],眾多學者使用神經網絡代替Q表格,采用DQN(deepQ-network)[15]等深度強化學習(deep reinforcement learning,DRL)算法進行訓練研究．為提高算法的性能,一些新穎的訓練技巧被應用到DQN中,例如董永峰等[16]通過動態融合DDQN(double deepQ-network)與averaged-DQN的先驗知識進行訓練,有效降低了過估計的影響,但算法總體迭代次數較多,對算力要求較高．姜蘭[17]提出了基于啟發式知識的DQN算法,有助于加速神經網絡的訓練,但該算法在運用啟發式知識時只考慮了避障而忽略了路徑規劃,致使規劃路徑過于冗余．丁志強[18]以DQN為基礎,編程實現了one-hot編碼狀態映射、縮減浮點數位數、調用SIMD指令集等,最終在路徑規劃仿真中提高了算法的運行速度．總體來說,上述的多數改進算法都是基于貪婪策略進行探索,為增強DQN算法的探索性能,Fortunato等[19]提出了noisynet-DQN算法,該算法將DQN網絡中的線性層替換成噪聲層取代傳統的貪婪策略, 通過增加較少的計算成本實現探索性能的極大提升, 但是這樣將導致算法的不穩定與計算能力的消耗．故本文借鑒noisynet-DQN的思想,在解決探索不足問題的前提下,保證算法的穩定與節省計算成本,并沒有在全部全連接層添加噪聲,只在輸出層中加入Gauss噪聲用于無人車避障．

此外,為了提升探索效率,本文將處理連續狀態的DQN算法加以變化地應用到離散狀態,并選擇在輸出層添加噪聲的三層全連接層作為Q網絡,避免了端對端處理模式對算力的依賴．考慮到有限的計算資源和算法落地的需求,本文選擇具有可遷移性的Gazebo仿真平臺對ROS無人車進行實驗仿真．仿真結果顯示此算法收斂速度、成功率與平均獎勵明顯高于Q-learning算法、DQN算法與noisynet_DQN算法, 證明了在此環境下加入單層噪聲的輕量級網絡的有效性, 并通過測試證明了算法在起始點、 目標點與障礙物方面具有泛化性能．

1 強 化 學 習

1.1 強化學習理論基礎

強化學習最初是受到心理學領域關于人類和動物學習方面的影響而形成的．在強化學習中,智能體從外部環境感知狀態(st),隨后智能體執行某動作(at),該動作改變環境中原來的狀態使智能體獲得一個新的狀態(st+1)．在新的狀態下,環境產生對智能體當前動作的獎勵(rt),此獎勵是對動作好壞的評價,隨后智能體根據獲得的狀態和獎勵修正動作策略并采取下一個動作,如此反復迭代,與環境通過反饋信息進行交互以獲得最大的累積獎勵(G=r1+r2+…+rn+…)．

1.2 DQN算法

深度強化學習是在強化學習的基礎上使用了神經網絡,使得原始感官輸入映射到原始電機輸出成為可能(圖1)．神經網絡具有良好的擬合能力,能夠通過簡單函數的組成逼近任意的非線性函數．在DQN中,Q網絡取代了Q-learning的Q表,將環境狀態利用非線性逼近映射成智能體的動作值．

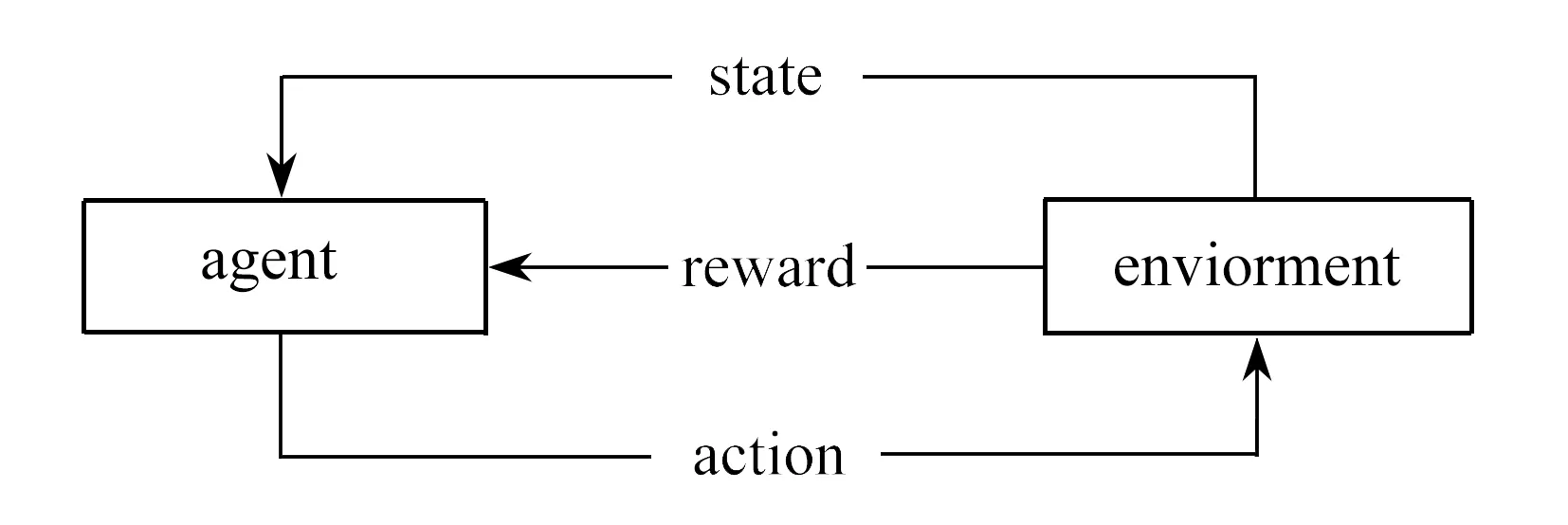
圖1 強化學習框架Fig. 1 The reinforcement learning framework

網絡架構、網絡超參數的選擇與學習都在訓練階段(Q網絡權重的學習)中完成．在訓練過程中,DQN通過經驗回放池來獲取訓練樣本,網絡的輸入是智能體接收到的從環境中傳來的狀態,輸出為智能體所有可能動作的Q值,隨后,采用ε-greedy貪婪策略來選擇動作并執行以平衡探索與利用之間的關系,環境根據所選動作反饋相應的獎勵,定義損失函數為目標Q值與Q值之間的差:

δloss=[r(st,at)+γmaxQ_(st+1,at+1)-Q(st,at)],

(1)

其中,maxQ_(st+1,at+1)表示當狀態為st+1時,在動作空間中選取恰當的動作得到的最大的行為值函數,Q_表示目標Q網絡．

對誤差進行反向傳播來更新Q網絡的參數,如此不斷進行訓練,直到誤差滿足特定條件或者到達迭代次數時學習結束．具體運行流程見文獻[15]．

2 算法模型設計

2.1 狀態空間與動作空間設計

將圖片作為輸入的端對端算法需要強大的算力支持,將連續狀態作為輸入的算法計算時間相對較長,考慮到探索效率和算法性能,本實驗采用離散化的思想,將連續狀態適度離散化為離散狀態,并作為算法的輸入．狀態的各分量劃分成確定數量的非重疊區域,不同區域代表著無人車面臨的不同環境信息．狀態為五維向量,分別為無人車前進方向與目標點的夾角、雷達傳感器在4個區域d1,d2,d3,d4中所感知到的障礙物的最近距離,即s=(θ,d1,d2,d3,d4),狀態示意圖如圖2所示．

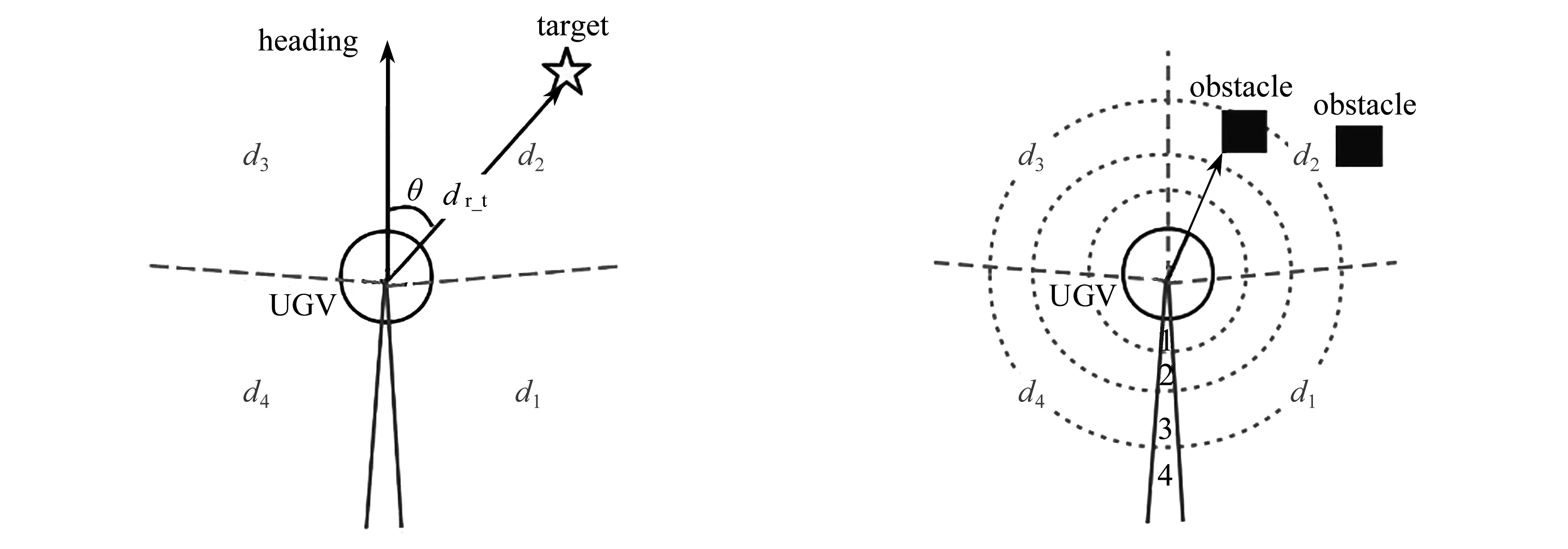
(a) 狀態向量各分量示意圖(b) d1～d4區域劃分圖(a) Schematic diagram of each component of the state vector(b) The zoning plan of d1～d4圖2 狀態示意圖Fig. 2 The state diagram

狀態分量具體劃分如下所示,共有3×4×4×4×4=768個狀態．

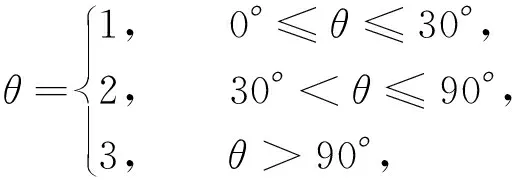
本實驗的動作空間為A,A中共包含4個動作: 前進、 后退、 右轉、 左轉, 具體為(0.5 m/s,0.0 rad/s),(-0.5 m/s,0.0 rad/s),(0.1 m/s,0.6 rad/s),(0.1 m/s,-0.6 rad/s),其中第一個分量表示線速度,第二個分量為角速度．

2.2 獎勵函數的設置

在強化學習中,獎勵函數是任務能否完美解決的重要因素,是無人車在某狀態下所采取動作的評價．本實驗的目的是使小車從初始點無碰撞且能夠快速地到達目標點,故獎勵函數的設置考慮到靠近目標點與遠離障礙物這兩個方面．

本文在文獻[16]獎勵函數的基礎上,加入漸進式的獎勵,這樣可使小車能夠更快地完成任務．具體為:當無人車碰到障礙物時,給予懲罰,獎勵為負值;當無人車到達目標點時,給予獎勵,獎勵為正值．為了促使小車一直向目標點移動,當小車運行一步后與目標點的距離比上一步離目標點的距離更近時,以及當小車進入目標點的某一范圍區域內時,給予正值獎勵;其余情況給予-2,是為了防止小車出現循環運動獲取值為1的獎勵．具體如下所示:

(2)

其中,dr_t(t)表示在t時刻無人車與目標點的距離,dr_o(t)表示在t時刻無人車距離障礙物的最近距離,do表示無人車撞到障礙物的閾值,dt表示實驗所設定的無人車到達目標點的閾值,dn表示所設定的無人車靠近目標點的閾值．

2.3 輸出層具有噪聲的DQN算法

對無人車進行路徑規劃時,當所有可達狀態處于可控(能夠迭代)并且能存儲在計算機RAM中時,Q-learning算法能夠很好地完成任務．然而,當環境中的狀態數超過計算機容量時,Q-learning算法中的Q表由于狀態數過多,容易出現維度爆炸的問題．這時,一般會選取DRL算法來完成任務．

對于本文所設計的僅有768個狀態的環境中,若使用Q-learning算法進行路徑規劃,雖不會出現維度爆炸問題,但狀態數過大易導致實驗效果較差;若使用復雜的深度強化學習算法,例如DDPG、 PPO等會導致計算機算力成本增加．通過實驗發現, 使用網絡結構簡單的DQN算法能夠更快更好地完成本文的路徑規劃任務．

因狀態數僅為768個,算法網絡層數過多會出現訓練時間長、收斂慢、浪費計算資源等問題．考慮到環境的復雜程度與計算效率,本文的算法網絡只有3層全連接層．為提高探索性能,本文受到文獻[19]的啟發,在網絡結構中加入Gauss噪聲;為保證算法的穩定性和節省計算成本,僅在輸出層添加分解Gauss噪聲．所添加的噪聲通過梯度下降法自動調整噪聲強度,減輕了對任何超參數調優的需要,并且噪聲所引發的探索程度是前后相關的,能夠根據每個權重方差在不同的狀態之間進行變化,此探索方法比DQN原本的ε-greedy貪婪策略隨機選擇動作的探索性能更好,既保證了探索動作多樣化,又提高了探索效率．具有p個輸入,q個輸出的全連接層添加噪聲后的具體表達式如下:

y=(μw+σw⊙εw)x+μb+(σb⊙εb),

(3)

其中,x∈Rp,y∈Rq,μw∈Rq×p,σw∈Rq×p,εw∈Rq×p,μb∈Rq,σb∈Rq,εb∈Rq,⊙表示逐元素乘法,εw,εb為隨機噪聲參數．

綜上所述,本文選擇在輸出層添加分解Gauss噪聲的三層全連接層的DQN算法．具體的算法流程如圖3所示．

圖3 在輸出層添加噪聲的DQN算法框架Fig. 3 The DQN algorithm framework for adding noise in the output layer

算法偽代碼如下所示．

算法1 輸出層添加分解Gauss噪聲的DQN算法

初始化經驗回放池D

隨機初始化Q網絡的參數θ、目標Q網絡的參數θ-與隨機噪音參數ε

for episode=1 to maxepisode do

觀測得到狀態s1

fort=1 toTdo

從Gauss分布中采樣得到噪聲ξ～ε

通過貪婪策略選擇動作at=maxQ(st,at,ξ;θ)

在環境中執行動作at

獲得獎勵rt并到達下一個狀態st+1

將經驗(st,at,rt,st+1)存儲到經驗回放池D中

令st=st+1

從經驗回放池中隨機采樣minibatch個經驗

forj=1 to minibatch do

從Gauss分布中采樣得到噪聲ξ′～ε

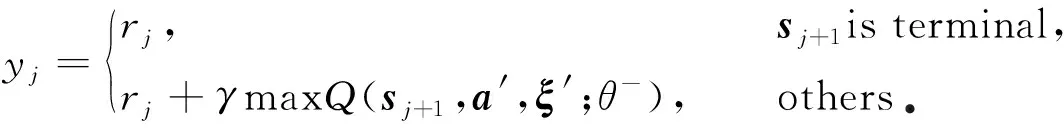
對(yj-Q(sj,aj,ξ″;θ))2執行梯度下降策略更新Q網絡的參數(ξ″～ε)

end for

每隔固定步數對目標網絡參數進行更新θ-=θ

end for

end for．

2.4 仿真環境

為計算方便起見,大多數文獻(例如文獻[12,16-18,20-21])選擇在柵格地圖等可視化環境中進行算法仿真,但這些仿真環境與現實環境有著較大的差別,致使實驗結果難以令人信服．近年來,越來越多的學者采用Gazebo等逼真的仿真環境進行實驗,例如文獻[22-25]．在柵格環境中進行實驗與Gazebo環境進行仿真相比,環境由二維平面轉換為三維空間,小車模型由一個點變為擁有動力學仿真和傳感器仿真的真實模型,環境和模型的變化可使Gazebo平臺的實驗結果更加真實可信．

故本算法選擇在Gazebo仿真環境下,使用基于機器人操作系統(ROS)搭建的差速式無人車進行實驗．本實驗中,在車體的前端安裝了一個雷達傳感器,可以檢測到車體周圍(-3 rad,3 rad)范圍內的環境信息,雷達傳感器的檢測有效范圍為0.10～30 m,精確到0.01 m,雷達旋轉一周發射360條射線,每一條射線進行一次測距,通過區域劃分,將傳感器感知到的范圍劃分成4個互不相交的區域,使用d1,d2,d3,d4表示無人車在4個區域內與障礙物的最短距離．計算無人車前進方向與目標點的夾角的絕對值的公式如下:

θ=|ψ-φ|,

(4)

其中,φ表示無人車前進方向與地圖坐標系x軸正方向的夾角,ψ表示目標點相對于無人車質心處地圖坐標系x軸正方向的夾角．

在Gazebo中建立了13×8單位距離的仿真環境,環境四周由墻圍住,中間設置6個障礙物,初始點為(0,0),目標點為(-6,1),Gazebo仿真環境如圖4所示,Rviz仿真環境如圖5所示．

圖4 Gazebo仿真環境 圖5 Rviz仿真環境 Fig. 4 The Gazebo simulation environment Fig. 5 The Rviz simulation environment

注為了解釋圖中的顏色,讀者可以參考本文的電子網頁版本,后同．

本實驗在UBUNTU操作系統上運行,處理器為Intel(R) Core(TM) i7-9700 CPU @ 3.00 GHz．無人車仿真使用PYTHON編程,Adam優化器進行網絡訓練優化．算法的網絡訓練參數設置如表1所示．

表1 算法訓練參數

本實驗的任務是利用在輸出層添加噪聲的DQN算法,使無人車在未知的環境中規劃出從初始點到目標點的無碰撞路徑．實驗共訓練1 000個回合,智能體執行一次動作的時間為1 s,無人車到達目標點或碰到障礙物則本回合結束．

3 實驗結果分析

為了驗證在輸出層添加噪聲的DQN算法在無人車路徑規劃中的有效性,采用PYTHON語言在Gazebo仿真環境中對Q-learning算法、DQN算法、3層全連接層都添加Gauss噪聲的DQN算法與僅在輸出層添加Gauss噪聲的DQN算法進行1 000回合的實驗．為區分算法的名稱,用changed_DQN表示在輸出層添加噪聲的DQN算法,noisynet_DQN表示Q網絡中的3層全連接層都添加噪聲的DQN算法．

圖6為采用Q-learning算法、DQN算法、changed_DQN算法與noisynet_DQN算法訓練1 000回合的成功率對比圖．從圖中看出,changed_DQN算法訓練效果最好,在100回合內成功率就開始快速提升,在200回合左右開始收斂,1 000回合時成功率為94.2%;Q-learning算法在訓練期間因狀態空間略大,訓練結果不穩定,成功率十分低,相比之下,3個DQN算法的成功率都遠高于Q-learning算法．依靠ε-greedy貪婪策略進行探索的DQN算法,成功率提升速度緩慢,1 000回合時成功率才71.6%,明顯低于另外兩種DQN算法,這表明在網絡結構中添加噪聲的DQN算法的探索效率高于使用ε-greedy貪婪策略的DQN算法;noisynet_DQN算法在前期探索階段成功率和changed_DQN相當,但后期因噪聲添加過多導致算法不好收斂,成功率明顯低于changed_DQN．

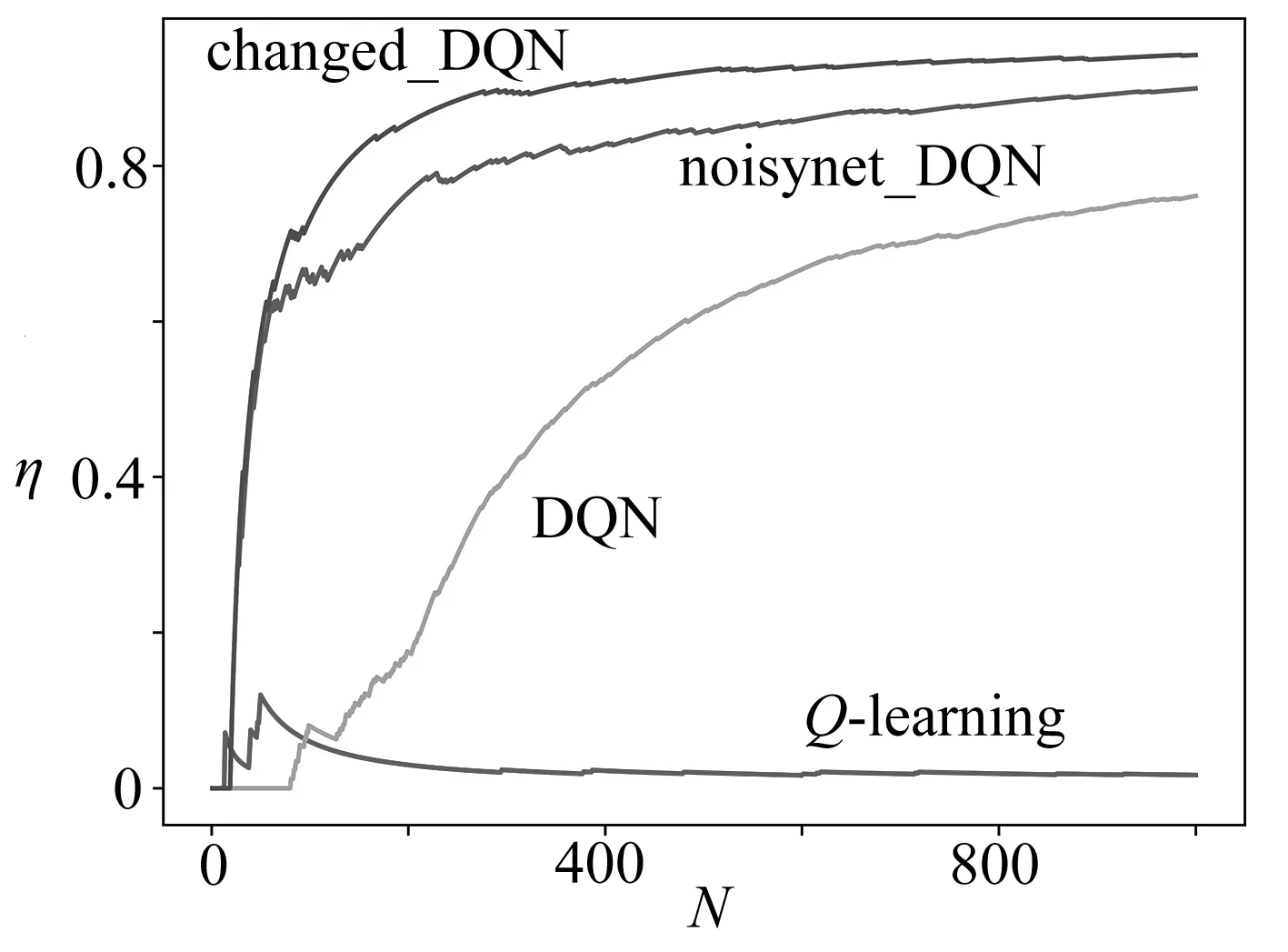
圖6 成功率對比圖Fig. 6 Comparison of success rates

訓練過程中每回合的平均獎勵對比如表2與圖7所示．從圖7(a)中可以看出,運用changed_DQN算法的小車所獲得的平均獎勵基本全部高于運用Q-learning算法的小車,且收斂在較高水平．從圖7(b)可看出,在前期100回合左右時,運用changed_DQN算法的小車的平均獎勵已經開始收斂,而運用DQN算法的小車的平均獎勵到400回合左右才開始收斂,且后期波動較大．從表2可看出,訓練過程中,changed_DQN算法的平均獎勵均值最大,方差最小,這說明此算法穩定并且獎勵收斂在較高的水平．

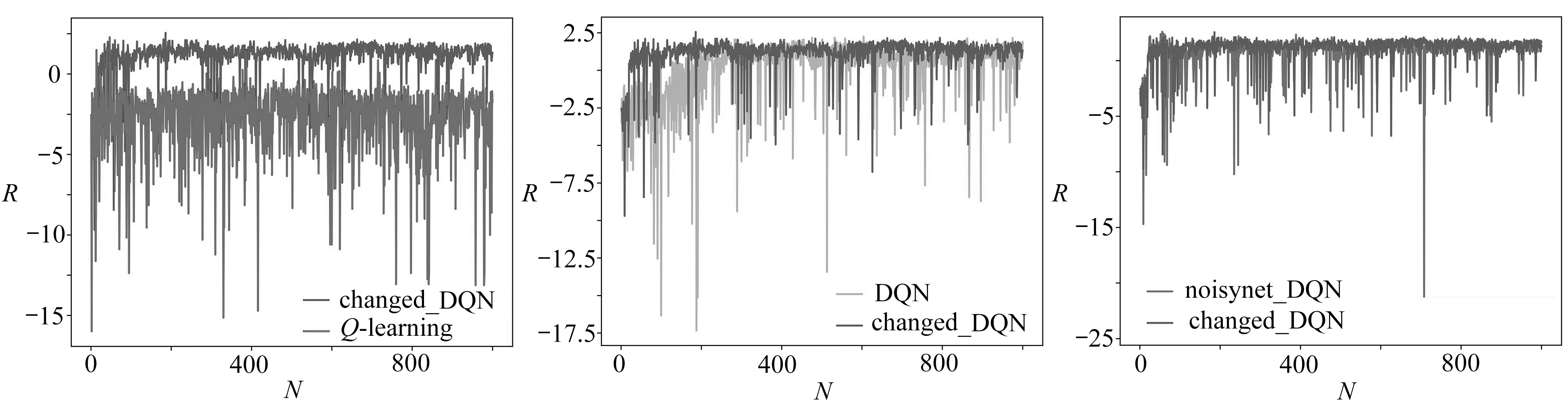
(a) Q-learning與changed_DQN (b) DQN與changed_DQN (c) Noisynet_DQN與changed_DQN 平均獎勵對比 平均獎勵對比 平均獎勵對比 (a) Mean reward comparison between (b) Mean reward comparison between (c) Mean reward comparison between Q-learning and changed_DQN DQN and changed_DQN noisynet_DQN and changed_DQN圖7 平均獎勵對比圖Fig. 7 Comparison of mean rewards

本實驗的目的為無人車能夠無碰撞地到達目標點,故選擇無人車結束本回合訓練時的位置與目標點的距離作為誤差,誤差越小表明越接近目標點．圖8(a)表明選擇changed_DQN算法的小車在50回合后可較好地完成任務,收斂后還有波動是由于動作策略的探索導致的,選擇Q-learning算法的無人車在訓練中的大多數回合都未完成任務．從圖8(b)的對比可知, changed_DQN算法比DQN算法收斂更快,且收斂后波動較小．從表3中可知,changed_DQN算法誤差的均值最小,方差最小,說明此算法穩定并且能更加精確地完成任務．

表3 誤差的均值與方差

(a) Q-learning算法與changed_DQN(b) DQN算法與changed_DQN (c) Noisynet_DQN算法與changed_DQN 算法誤差對比 算法誤差對比 算法誤差對比 (a) Error comparison between Q-learning (b) Error comparison between DQN (c) Error comparison between noisynet_DQN and changed_DQN and changed_DQN and changed_DQN圖8 誤差對比圖Fig. 8 Error comparison diagrams

對訓練好的算法進行50次測試實驗,Q-learning、DQN、changed_DQN與noisynet_DQN算法的成功率分別為46%,98%,96%,94%,從實驗結果可以看出訓練好的changed_DQN算法成功率略低于DQN算法,但相差不大(圖9)．從完成任務的規劃時間來看,changed_DQN算法所需時間穩定且總體低于其他算法(圖10)．這表明changed_DQN算法具有高效性．

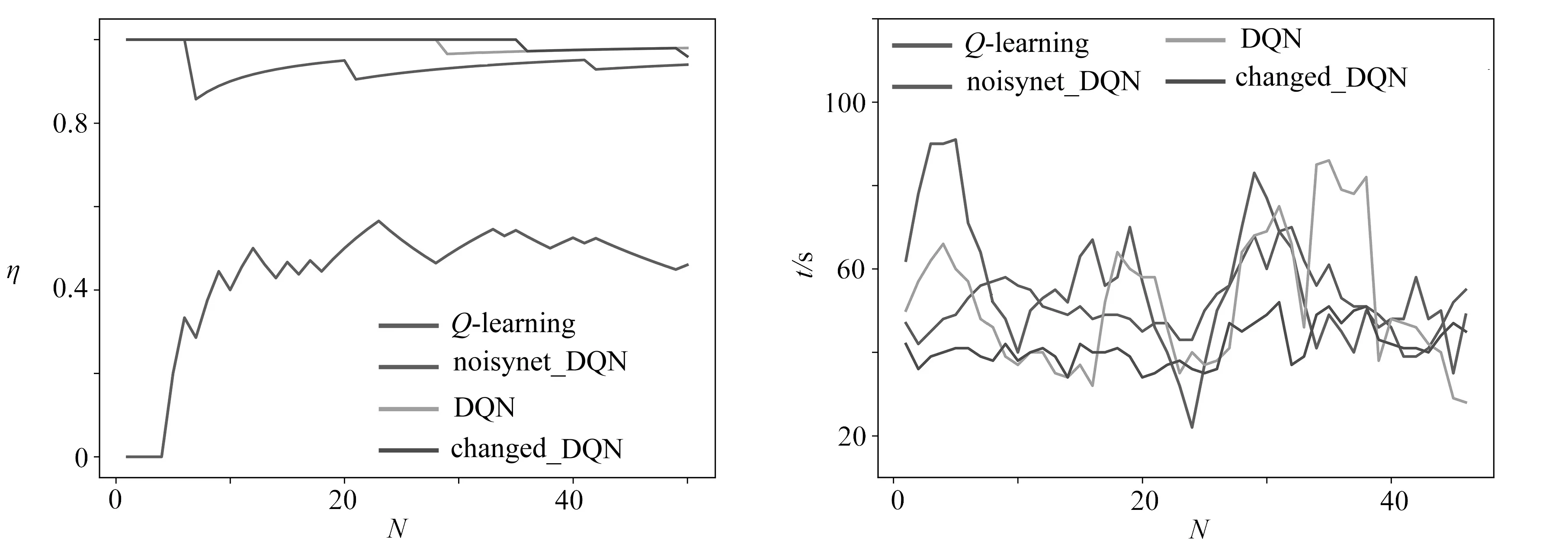
圖9 測試實驗成功率 圖10 測試實驗規劃時間 Fig. 9 Success rates of testingFig. 10 Programming time of testing

圖11、12分別為Q-learning算法和changed_DQN算法在1 000回合左右的路徑圖．路徑圖以初始點為原點,運用Q-learning算法的小車在1 000回合左右未能規劃出從初始點到目標點的無碰撞路徑,運用changed_DQN算法的小車能規劃出較為完美的無碰撞路徑．

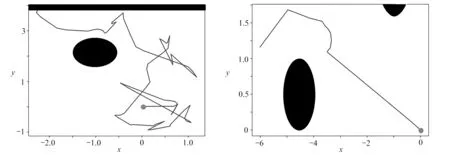
圖11 Q-learning算法路徑規劃效果圖圖12 Changed_DQN算法路徑規劃效果圖Fig. 11 Path programming effects based on Fig. 12 Path programming effects based on Q-learning changed_DQN

為了驗證在輸出層添加噪聲的DQN算法的有效性和魯棒性,分別在改變起始點、改變目標點和改變障礙物的環境中進行仿真實驗．仿真結果表明,運用changed_DQN算法的無人車均能快速地找到從起始點到目標點的相對較優的無碰撞路徑．圖13、14、15分別為改變起始點、目標點和障礙物的路徑規劃圖．圖16為障礙物改變后的Gazebo仿真環境．

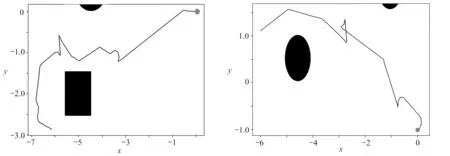
圖13 目標點改變時changed_DQN算法路徑規劃效果圖 圖14 起始點改變時changed_DQN算法路徑規劃效果圖 Fig. 13 Path programming effects based on changed_DQN Fig. 14 Path programming effects based on changed_DQN with changing target point with changing starting point

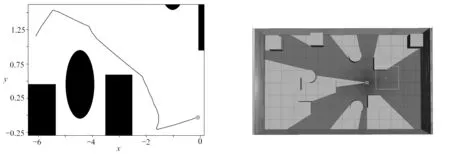
圖15 障礙物改變后的changed_DQN算法路徑規劃效果圖 圖16 障礙物改變后的Gazebo仿真環境Fig. 15 Path programming effects of changed_DQN after Fig. 16 The Gazebo simulation environment after the obstacle change the obstacle change

4 結 束 語

本文針對離散狀態空間中狀態數量較多的無人車路徑規劃問題,提出了在輸出層添加分解Gauss噪聲的DQN算法進行路徑規劃,該算法節省了計算成本,平衡了探索與利用．仿真實驗表明,算法的收斂速度和規劃路線的優越性都高于處理狀態離散問題常用的Q-learning算法,且誤差收斂到0的速度更快,誤差更小,通過與DQN、noisynet_DQN算法實驗對比發現,本文所采用的算法成功率更高,效果更好．在初始點、目標點和障礙物方面對本文的算法進行了泛化性能的測試,驗證了該策略的有效性和魯棒性．