具有時滯的離散Lotka-Volterra合作系統波前解的非線性穩定性*
閆 瑞, 劉桂榮, 李曉翠
(1. 山西財經大學 應用數學學院, 太原 030006;2. 山西大學 數學科學學院, 太原 030006;3. 北京化工大學 數理學院, 北京 100029)
0 引 言
由專著[1]可知在實際應用中,許多物理學、化學、生物學、傳染病學等問題都可以歸結為反應擴散方程.所以,研究反應擴散方程的相關內容對生產實踐和科學理論具有重要的意義.近年來,關于具有時滯的反應擴散系統的研究是一個重要的課題.因此,本文主要研究如下具有時滯的離散Lotka-Volterra合作系統:
(1)
其中x∈,t∈+,D[w(x,t)]=w(x+1,t)+w(x-1,t)-2w(x,t),w=u,v,所有系數都是正的且時滯τ>0.這里u(x,t)和v(x,t)分別代表x位置和t時刻的人口密度.其初值條件為
(2)
事實上,系統(1)可以認為是如下系統的空間離散化形式:
(3)
顯然,系統(1)有4個可能的平衡點
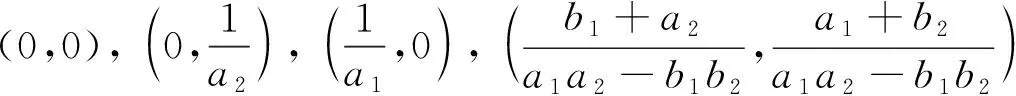
易知,當a1a2-b1b2>0時,ki>0(i=1,2),在系統(3)對應的無擴散系統中,平衡點(0,0)是不穩定的,而平衡點(k1,k2)是穩定的.
在離散方程和系統的研究中,行波解的相關研究也是熱點問題之一.對于系統(1) 的連接(0,0)與(k1,k2)的行波解指的是具有如下形式:
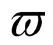
且滿足
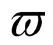
關于不同類型的擴散系統的行波解存在性研究已有了大量的結論,可參考文獻[2-8].在關于行波解的研究中,除存在性外,行波解穩定性也是一個比較有趣和困難的問題.關于這方面的研究可參考文獻[9-15].對于帶有時滯的反應擴散方程,Schaaf首先通過譜分析方法研究了該類方程的行波解的線性穩定性[16].Mei等[17]則利用加權L2能量估計的方法證明了具有時滯的Nicholson方程波前解的非線性穩定性.接著,Mei等在文獻[18-20]中應用加權能量法和比較原理,研究了一般的帶有時滯的單穩反應擴散方程行波解的全局穩定性.之后,Yu等[21]和Zhang等[22]將加權能量法證明波前解穩定性的方法推廣到不同的非局部擴散系統.此外,對于離散擴散方程的行波解的穩定性的研究可以參考文獻[23-26].對于離散擴散系統,最近,Chen等[27]及Su等[28]分別運用加權能量結合比較原則證明了一個三種群離散擴散競爭系統的單穩波前解的非線性穩定性.而在文獻[29]中,Hsu等運用不同的比較定理,研究了一些離散反應擴散系統行波解的穩定性,這些結論可以廣泛應用到諸如多種群Lotka-Volterra合作模型、流行病模型、三種群Lotka-Volterra競爭模型等.但是,目前關于系統(1)的波前解穩定性并沒有任何的結論,因此,受文獻[17-20]的啟發,本文將通過加權能量的方法研究該系統波前解的全局穩定性.
本文的主要內容安排如下: 第1節給出了一些預備知識和符號,并給出了波前解穩定性的主要結果;第2節給出了穩定性的證明;最后給出了本文的結論.
1 預備知識和主要結果
在本節中,我們將引入一些記號以方便敘述并給出主要結論.首先,在本文中,C>0代表一個一般的常數,Ci>0代表具體的常數,I是一個區間,通常I=.其次,L2(I)表示I上的平方可積函數構成的空間,若函數f(x)且其導數dif/dxi(i=1,2,…,k)都屬于L2(I),則這些函數構成Sobolev空間Hk(I)(k≥0).進一步,表示加權的L2空間(ω(x)>0),其范數為

令T為一個正常數,B是一個Banach空間.C([0,T];B)表示由[0,T]上的B-值連續函數構成的空間.L2([0,T];B)表示由[0,T]上的B-值L2-函數構成的空間.[0,∞)上的空間可以類似地給出.
接下來,對于λ>0,c>0,定義
Δi(c,λ)=di(eλ+e-λ-2)-cλ+ri,i=1,2.
引理1[30]存在唯一常數c*>0使得
1) 對于任意c>c*,Δ1(c,λ)=0有兩個實根0<λ1(c)<λ2(c),且當λ∈(λ1(c),λ2(c)) 時,Δ1(c,λ)<0,當λ∈+[λ1(c),λ2(c)] 時,Δ1(c,λ)>0;
2) 對于任意c>c*,Δ2(c,λ)=0有兩個實根0<λ3(c)<λ4(c),且當λ∈(λ3(c),λ4(c))時,Δ2(c,λ)<0,當λ∈+[λ3(c),λ4(c)]時,Δ2(c,λ)>0;
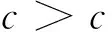
3) 對于任意0≤c
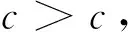
另外,當a1a2-b1b2>0,d1≤d2,r1≤r2時, 對于c>c*, 系統(1)存在連接(0,0)和(k1,k2)的波前解.對于0 在文獻[30]的基礎之上,本文將進一步研究系統(1)波前解的穩定性.首先給出如下假設: (A1)a1a2-b1b2>0,d1≤d2,r1≤r2, 2r1-d1>0, 2r2-d2>0; (A2) 4a1r1k1>2r1(1+2b1k2)+b1r1k1+b2r2k2+d1, 4a2r2k2>2r2(1+2b2k1)+b1r1k1+b2r2k2+d2. 注1 令a1=2,a2=2.5,b1=1,b2=1,r1=1.5,r2=2,d1=0.1,d2=0.2,通過計算可知假設(A2)是成立的. 為了給出加權能量函數及適當的估計,在此我們定義如下兩個關于β的函數: f1(β)=4a1r1k1-2r1(1+2b1k2)-b1r1k1-b2r2k2-d1(eβ+e-β-1), f2(β)=4a2r2k2-2r2(1+2b2k1)-b1r1k1-b2r2k2-d2(eβ+e-β-1). 由假設(A2),易得 f1(0)=4a1r1k1-2r1(1+2b1k2)-b1r1k1-b2r2k2-d1>0, f2(0)=4a2r2k2-2r2(1+2b2k1)-b1r1k1-b2r2k2-d2>0. 再由fi(β)(i=1,2)的連續性,知存在β0>0,使得f1(β0)>0和f2(β0)>0.之后再定義另外兩個關于ξ的函數: g1(ξ)=-2r1(1+2b1k2)-b1r1k1-b2r2k2+4a1r1φ(ξ)-d1(eβ0+e-β0-1), g2(ξ)=-2r2(1+2b2k1)-b1r1k1-b2r2k2+4a2r2ψ(ξ)-d2(eβ0+e-β0-1), 其中(φ(ξ),ψ(ξ))是系統(1)的波前解.易得 于是存在足夠大的ξ0>0,使得 gi(ξ0)>0,i=1,2. (4) 由上文,我們進一步定義如下的關于β0和ξ0的加權函數: 最后,我們給出本文的主要結論,即系統(1)的波前解的指數穩定性. 定理1 假設(A1)和(A2)成立.令 其中 c1=2r1(1+2b1k2)+b1r1k1+b2r2k2+d1(eβ0+e-β0-1), c2=2r2(1+2b2k1)+b1r1k1+b2r2k2+d2(eβ0+e-β0-1). 0≤u0(x,s)≤k1, 0≤v0(x,s)≤k2, (x,s)∈×[-τ,0], 0≤u(x,t)≤k1, 0≤v(x,t)≤k2, (x,t)∈×+, 其中常數μ>0. 本節將通過加權能量的方法證明本文的主要結論.首先,類似文獻[22,27]中的證明,我們可以給出系統(1)的存在性定理和比較原理. 引理2 假設a1a2-b1b2>0, 2r1-d1>0, 2r2-d2>0成立,若初始條件滿足 (0,0)≤(u0(x,s),v0(x,s))≤(k1,k2), (x,s)∈×[-τ,0], 那么Cauchy問題(1)、(2)的解存在唯一且滿足 (0,0)≤(u(x,t),v(x,t))≤(k1,k2), (x,t)∈×+. 那么 若(u0(x,s),v0(x,s))滿足 (0,0)≤(u0(x,s),v0(x,s))≤(k1,k2), (x,s)∈×[-τ,0], 令 (5) 那么 (6) (7) 接下來將分三步來證明主要的結果. 首先,證明u+(x,t)收斂到φ(x+ct).令 其中ξ=x+ct.由式(5)和(6),有 (0,0)≤(U(ξ,t),V(ξ,t))≤(k1,k2), (0,0)≤(U0(ξ,s),V0(ξ,s))≤(k1,k2). 通過計算易得U(ξ,t),V(ξ,t)滿足 (8) 式(8)的方程兩端分別乘以e2μtω(ξ)U(ξ,t)和e2μtω(ξ)V(ξ,t),其中μ>0待定,可得 -a1r1e2μtωU3+b1r1φe2μtωUV(ξ-cτ,t-τ), (9) -a2r2e2μtωV3+b2r2ψe2μtωVU(ξ-cτ,t-τ). (10) 因此,對式(9)和式(10)分別關于ξ和t在×[0,t]上積分可得 (11) (12) 由Cauchy-Schwarz不等式可得 (13) 其中W=U,V.類似地,對于式(11)和式(12)右端的第二項,有 (14) (15) 將式(13)—(15)代入到式(11)和(12)中,由于對于ξ∈有ω(ξ+cτ)/ω(ξ)≤1,因此 (16) (17) 結合式(16)與式(17),可得 (18) 其中 類似地,當ξ0-1≤ξ≤ξ0時,此時ω(ξ+cτ)/ω(ξ)≤1.然后可得 當ξ0<ξ≤ξ0+1時,此時ω(ξ+cτ)/ω(ξ)=1.然后可得 當ξ>ξ0+1時,此時ω(ξ+cτ)/ω(ξ)=1.然后可得 □ 引理4 設μ1>0是如下方程 (19) 證明由于(0,0)≤(φ(ξ),ψ(ξ))≤(k1,k2)及ω(ξ+cτ)/ω(ξ)≤1(ξ∈),因此,當0<μ<μ1時,可得 □ 然后,將式(19)代入式(18),我們可得如下估計. (20) 之后,我們給出Uξ和Vξ在加權空間中的L2估計.類似地,對式(8)方程兩端關于ξ求導并對所得方程的兩邊分別乘以e2μtω(ξ)Uξ(ξ,t)和e2μtω(ξ)Vξ(ξ,t),可得 r1e2μtωUUξ[2a1φ′-b1ψ′(ξ-cτ)-b1Vξ(ξ-cτ,t-τ)]= r2e2μtωVVξ[2a2ψ′-b2φ′(ξ-cτ)-b2Uξ(ξ-cτ,t-τ)]= 重復上述證明過程可得引理6. 由引理5和6,可得到如下估計. 由于ω(ξ)≥1,運用Sobolev嵌入定理H1()C(),我們得到如下衰減結論. 其次,重復上述證明過程可得引理9. 最后,運用擠壓定理并結合引理8與9,可證明定理1成立. 本文運用L2-加權能量方法、比較原理和擠壓技術得到了具有時滯的離散Lotka-Volterra合作系統波前解的全局指數穩定性,并解決了離散擴散算子及時滯共同作用下建立能量估計的問題.此穩定性結果可以有助于理解解(u,v)漸近地表現為以正速度c傳播的行波解,并且隨著時間t的推移,這兩個物種趨于合作水平.
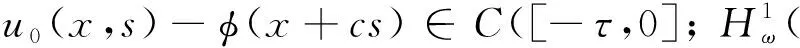
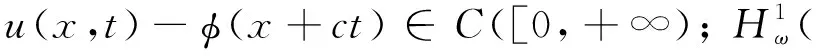
2 穩定性的證明
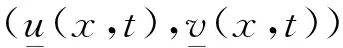

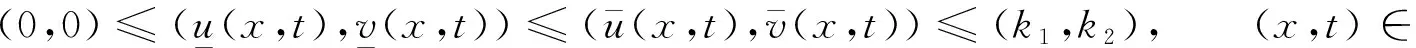
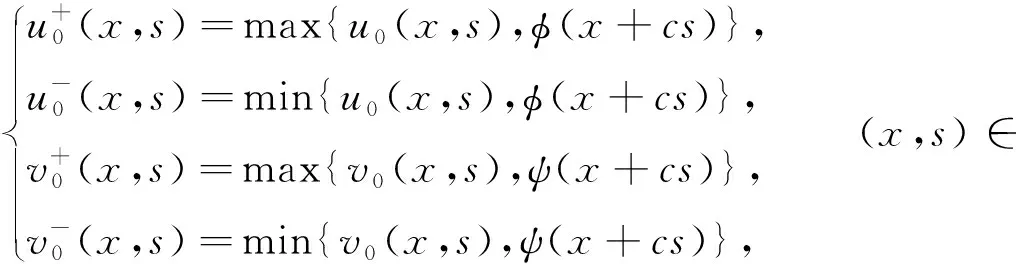
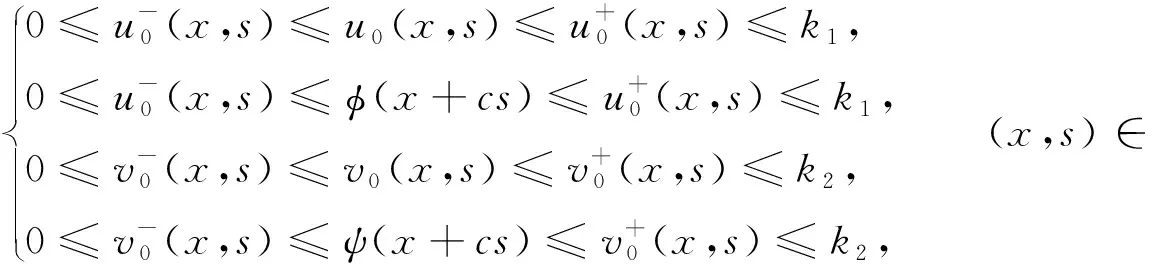
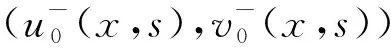
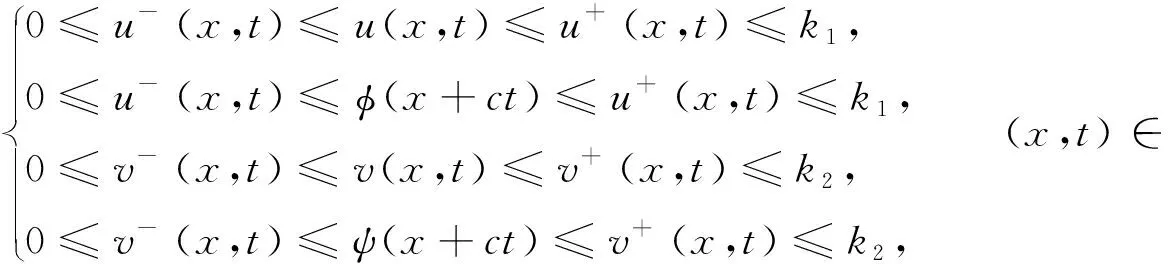
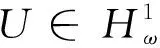
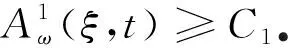
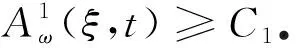
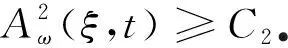
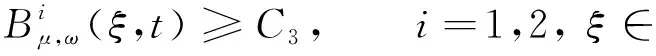
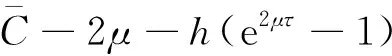




3 結 論

