熱傳導問題雜交基本解有限元法虛擬源點的探究*
張 凱, 王克用, 齊東平
(上海工程技術大學 機械與汽車工程學院, 上海 201620)
0 引 言
雜交Trefftz有限元法(HT-FEM)最早由Jirousek和Leon[1]在對薄板體彎曲問題的研究中提出,該方法融合了傳統有限元法(FEM)和邊界元法(BEM)的諸多優點,并且摒棄了它們的一些缺點[2-4].對于某些物理問題,雜交Trefftz有限元法很難得到相應的完備解,且需要選擇合適的Trefftz項數來獲得預期結果.為克服這一缺點,近年來,基于基本解的雜交有限元法(HFS-FEM)得到了廣泛的關注[4-6].與雜交Trefftz有限元法相似,雜交基本解有限元法也假設兩個獨立的溫度場:單元域內溫度場和單元邊界網線場.不同之處在于,后者利用控制方程基本解的線性組合來近似單元域內場,而前者采用完備解.引入修正變分泛函將上述兩個場關聯起來,導出僅含邊界積分的有限元列式,降低了求解維度,從而減少了計算量,稀疏網格下也能獲得理想的精度[6-11].顯然,該方法幾乎繼承了雜交Trefftz有限元法的所有優點,且規避了難以構造Trefftz函數的問題.到目前為止,雜交基本解有限元法已成功應用于熱傳導問題[4]、平面彈性問題[12]、熱彈性問題[13]、軸對稱問題[7-8,14]和裂紋問題[15]等.
由于基本解的奇異性[16],適當數量的源點需布置在單元域外,以避免基本解涉及奇異積分問題.根據以往的研究,源點的布局主要有兩種方式:一種是假設與單元邊界形狀相似的虛擬邊界(偏置邊界),另一種是在單元域外假設一個圓形虛擬邊界[17].虛擬邊界偏移量和源點數目的選擇直接影響計算結果的準確性和穩定性,需要根據問題具體分析,目前尚無準確的數值供選擇.上述雜交基本解有限元法均采用第一種虛擬邊界求解問題,而對其他源點布局未作闡述.在求解扭轉彈性問題[18]中,通過對比上述兩種邊界方式下的計算結果,認為當源點布局方式與單元域形狀相似時,可得到良好的結果.
在問題求解中,一種源點的方案可能不適用于所有的問題,當其失效時,可以考慮其他源點布局方式.為了探究不同源點對雜交基本解有限元法的影響,本文結合上述兩種虛擬邊界以及雙重虛擬邊界[19]分析了熱傳導問題.通過兩個算例驗證了不同源點布局方式的可行性,探討了源點數目和偏移量對計算精度的影響,以及虛擬邊界參數對單元剛度矩陣條件數的影響,同時也分析了不同源點布局下的收斂性.此外,還說明了當網格畸變程度較大時,哪種源點布局更適合求解.
1 問 題 描 述
1.1 控制方程與邊界條件
對于穩態熱傳導問題,一般二維區域Ω的Laplace控制方程為
(1)
考慮Dirichlet和Neumann邊界條件:
(2)
(3)
式中,u和q分別代表未知溫度和熱流,字母上方的橫線代表已知邊界值,k為導熱系數,Γ=Γu∪Γq為求解域Ω圍成的整個邊界,nx1和nx2分別代表邊界Γ上任意點外法線方向余弦,x=[x1,x2]T.
1.2 基本解及源點布局
對于均質各向同性材料,Laplace方程(1)的基本解[4,13]為
(4)
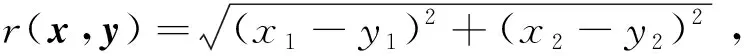
類型1 單元域外假想一個與單元邊界形狀相似的虛擬邊界,源點ysj(j=1,2,…,ns)位置可由基本解法確定:
ysj=xb+λ(xb+xc),
(5)
式中,λ為無量綱參數,決定著源點到單元邊界的距離,xb為單元邊界上的場點,xc為單元形心.圖1(a)為一個典型的單元源點分布.
類型2 單元域外假想一個半徑為R的圓形虛擬邊界,其形式如圖1(b)所示,源點和場點滿足下列方程式:
(6a)
(6b)
類型3 雙層虛擬邊界,與類型2類似,在單元域外假想兩個半徑分別為R1和R2的圓,其形式如圖1(c)所示,源點分別布置在兩個圓上:
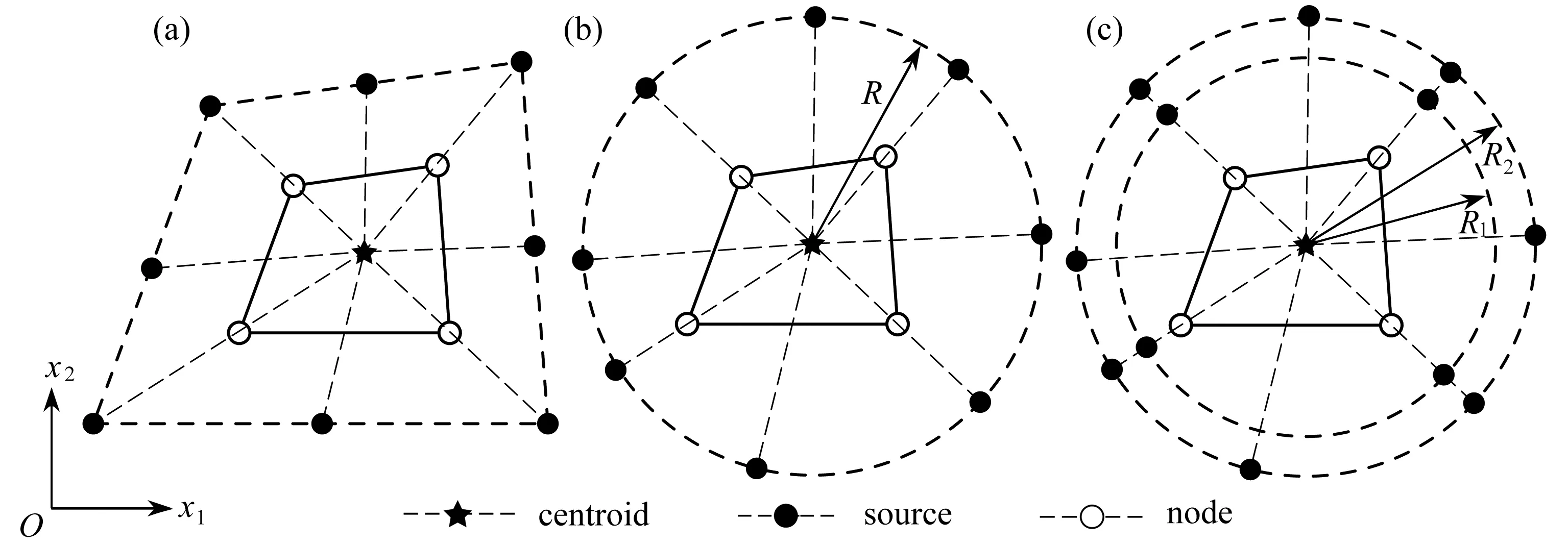
圖1 源點配置方式Fig. 1 Configurations of source points
(7a)
(7b)
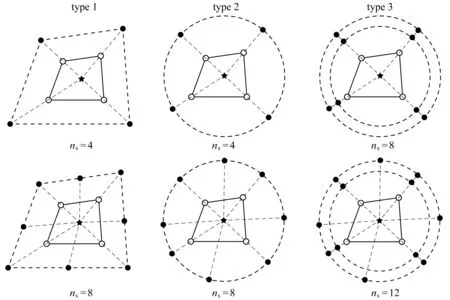
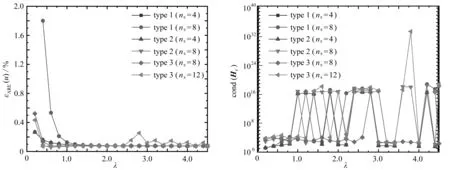
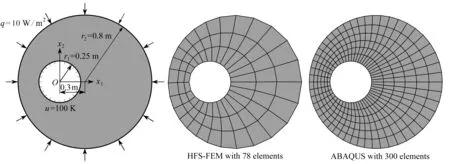
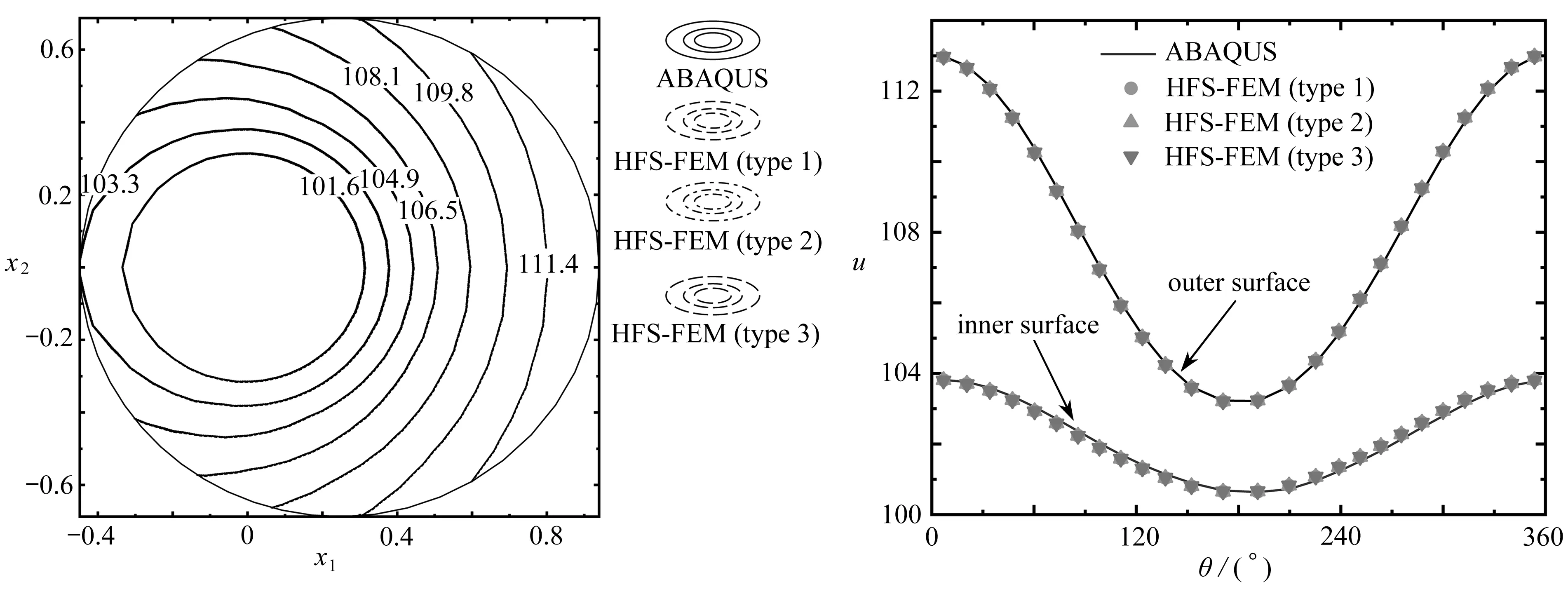
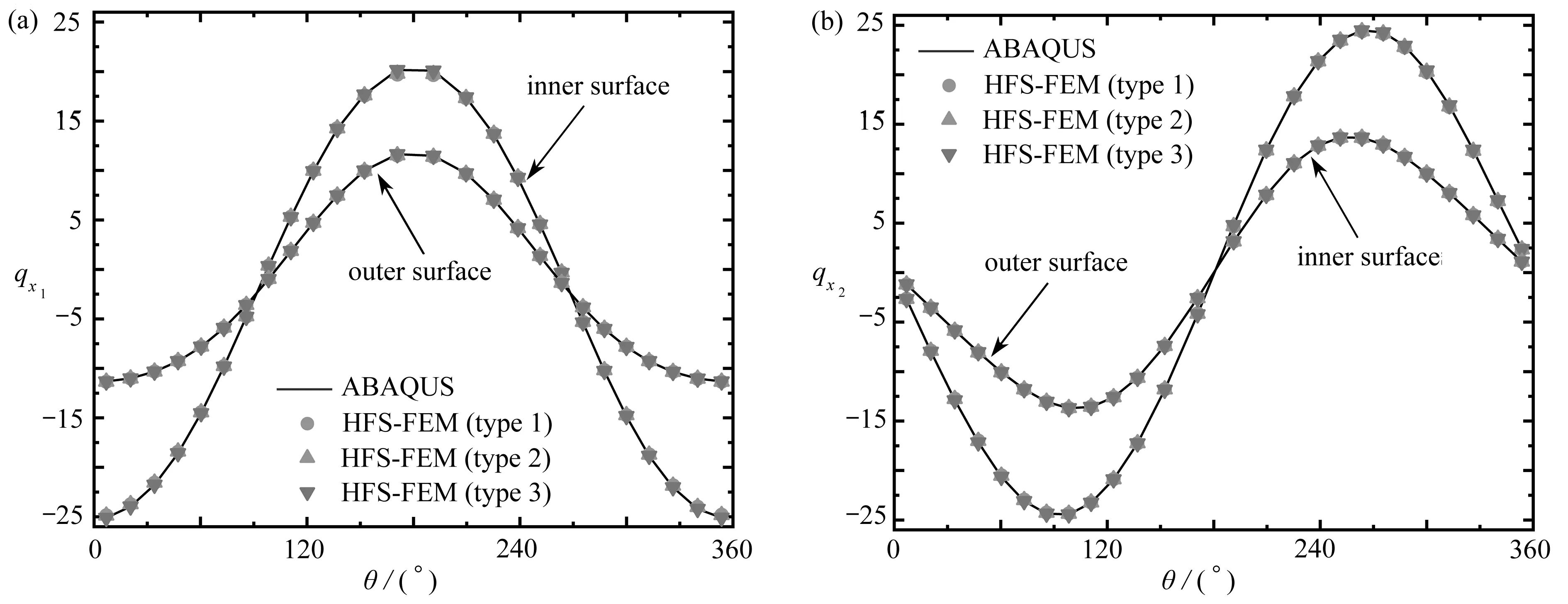
式中,θ為單元邊界節點的角度.為了便于區分,假設R1 為了更好地對源點布局進行比較分析,構造了以無量綱參數λ為變量的關系式: (8) 式中,dmax為單元邊上點到單元形心的最大距離,d為雙層虛擬邊界之間的距離,即d=R2-R1=αR2,若無特殊說明,α=0.1. 類似于Trefftz有限元法,雜交基本解有限元法將所考慮的問題域劃分為一系列小的單元,采用兩個獨立的插值模式(單元域內溫度場和輔助網線溫度場).圖2為一個典型的四節點單元.單元域內溫度場由基本解的線性組合構成,保證了單元域內變量場的計算精度; 單元邊界定義的輔助網線溫度場確保了單元間的連續性,一般采用常規有限元法的形函數[7]. 1) 單元域內溫度場 (9) 式中,ue為單元域內的溫度,Ne為基本解Ne(x,yj)=u*(x,y)的線性組合構成的行向量,ns為單元域外源點個數,ce為待定參數構成的列向量,Ωe為單元邊界Γe圍成的單元區域. 利用式(9),單元邊界Γe上的外法向熱流qe為 (10) 式中 (11) 2) 輔助網線溫度場 (12) 圖2 典型四節點單元和單元邊形函數Fig. 2 A typical 4-node element and the element side shape functions (13) 整個求解域Ω的雜交泛函Πm為所有單元泛函Πme的疊加,即Πm=∑eΠme.為將上述兩個溫度場關聯在一起,單元泛函可表示為 (14) (15) 將式(9)、(10)和(12)代入式(15),有 (16) 式中 (17) 為保證單元間連續性,未知向量ce由單元節點自由度向量de表示,對泛函(16)應用駐值原理分別消去ce和de,即 (18) (19) ue=c0+Nece, (20) (21) 進一步得知 (22) 式中,ne為單元的節點個數,一旦通過整體剛度矩陣求得節點的溫度,向量ce即可通過式(18)確定,然后c0可由式(22)求得,最后可通過式(20)求出單元域內任一點的溫度ue. 為驗證不同源點布局方式下本文方法的可行性,考慮了兩個數值算例:正方形板和偏心環空的熱傳導.若無特別說明,導熱系數取為k=1 W/(m·K).為了從量化角度理解計算結果的準確性,引入了任意變量f的平均相對誤差(ARE): (23) 式中,Nt為測試點的數目,(fHFS-FEM)i和(fref)i分別為雜交基本解有限元法和ABAQUS在點i的數值解. 第一個算例考慮的是正方形板,其幾何尺寸和邊界條件如圖3所示.板的上下表面均施加Dirichlet邊界條件,右表面施加Neumann邊界條件.為研究該方法的收斂性,將正方形板分別離散為2×2,4×4,6×6和8×8網格. 圖4 不同源點數目的四節點單元Fig. 4 A 4-node element with different numbers of source points 圖5 無量綱參數λ對計算精度的影響 圖6 無量綱參數λ對矩陣He條件數的影響 Fig. 5 Effects of dimensionless parameter λ on Fig. 6 Effects of dimensionless parameter λ on the computation accuracy the condition number of matrix He 為研究本文方法對網格畸變的不敏感性,圖7給出了5種4×4網格畸變方案,由無量綱參數ψ=e/l決定網格的畸變程度.圖8給出了溫度的平均相對誤差隨著畸變程度的變化情況,盡管網格畸變程度較大,該方法仍能得到良好的計算結果,這主要得益于修正變分泛函僅涉及邊界積分.從圖9可以看出,采用不同源點布局方式的計算結果收斂的趨勢是相同的,而采用雙重虛擬邊界收斂的速度更快一些.表1和表2分別給出了若干點的溫度和沿著x2方向的熱流分量,盡管個別點熱流誤差較大,但仍在工程實際容許范圍內,并且隨著網格的加密,精度會逐漸改善. 圖7 網格畸變方案Fig. 7 Mesh distortion schemes 圖8 畸變程度ψ對計算精度影響 圖9 網格密度對計算精度的影響 Fig. 8 Effects of distortion parameter ψ on Fig. 9 Effects of the mesh density on the computation accuracy the computation accuracy 表1 選擇點處溫度u的計算結果 表2 選擇點處熱流分量qx2的計算結果 為驗證本文方法求解曲邊問題的有效性,第二個算例考慮偏心環空的熱傳導.該算例的尺寸參數和邊界條件如圖10所示,內表面施加Dirichlet邊界條件,外表面施加Neumann邊界條件.在計算過程中,整個求解域離散為78個4節點四邊形單元.為便于比較,將采用300個單元的ABAQUS數值解作為參考解. 圖10 偏心環空與有限元網格Fig. 10 An eccentric annulus and the finite element meshes 圖11給出了不同源點布局下雜交基本解有限元法采用78個單元的溫度等值線圖,可以看出與ABAQUS數值結果吻合較好.為了使數據可視化,圖12和13給出了不同源點布局下偏心環空內表面和外表面單元形心的周向溫度及其熱流分量qx1和qx2的計算結果,與ABAQUS數值解對比發現,兩者結果基本吻合,進一步說明了本文方法在稀疏網格下仍能得到滿意的結果.為說明該方法的效率,表3列出了CPU計算所需的時間,所有的計算都是在戴爾靈越15-1558(處理器類型:Intel Core i7-5500U)上進行的.與ABAQUS相比,HFS-FEM計算所需的時間更少,這表明該方法具有更高的效率. 圖11 偏心環空溫度u的等值線圖 圖12 單元形心處溫度u沿周向的變化Fig. 11 Contour plots of temperature u in Fig. 12 Variations of temperature u at element centroids the eccentric annulus along the circumferential direction 表3 CPU時間的對比 圖13 單元形心處熱流分量qx1和qx2沿周向的變化Fig. 13 Variations of heat flux components qx1 and qx2 at element centroids along the circumferential direction 對于熱傳導問題,本文基于雜交基本解有限元法,分別采用3種源點布局方式(與單元形狀相似的虛擬邊界、圓形虛擬邊界和雙重虛擬邊界)進行求解,所得結論如下: 1) 相比于單元偏置的虛擬邊界和圓形邊界,隨著網格的加密,采用雙重虛擬邊界的收斂性更好. 2) 對于網格畸變程度較大的算例,圓形虛擬邊界更適合用來求解. 3) 隨著源點與邊界距離的增加,8源點雙重虛擬邊界下,靠近單元邊界趨于穩定更快,并且其矩陣條件數的上下振蕩次數較小.對于另外兩種方法,盡管矩陣條件數較小,但其數值振蕩次數較大. 本文通過兩個數值算例,與傳統有限元法計算結果對比.驗證了3種源點布局方式的可行性,在稀疏網格下,雜交基本解有限元法仍能獲得較高的精度.2 雜交有限元列式
2.1 假設溫度場
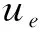
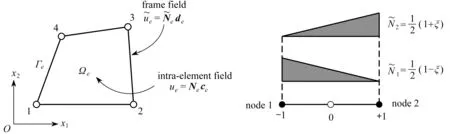
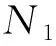
2.2 修正變分泛函
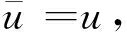
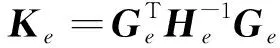
2.3 恢復剛體運動項
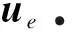
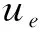
3 數 值 算 例
3.1 正方形板
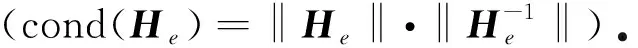
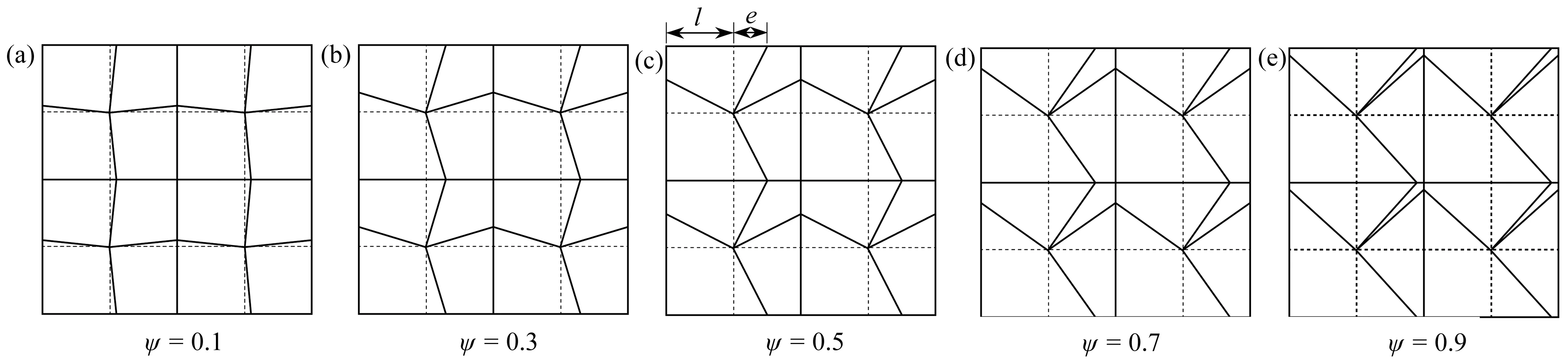
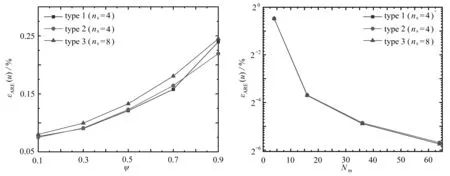
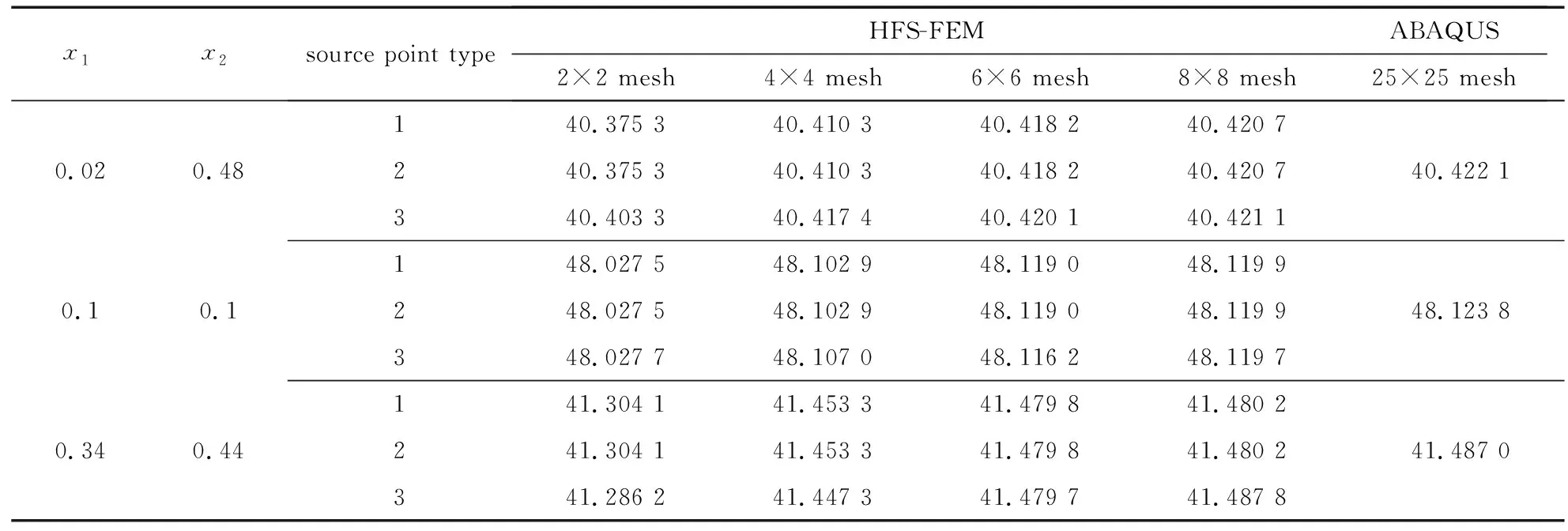
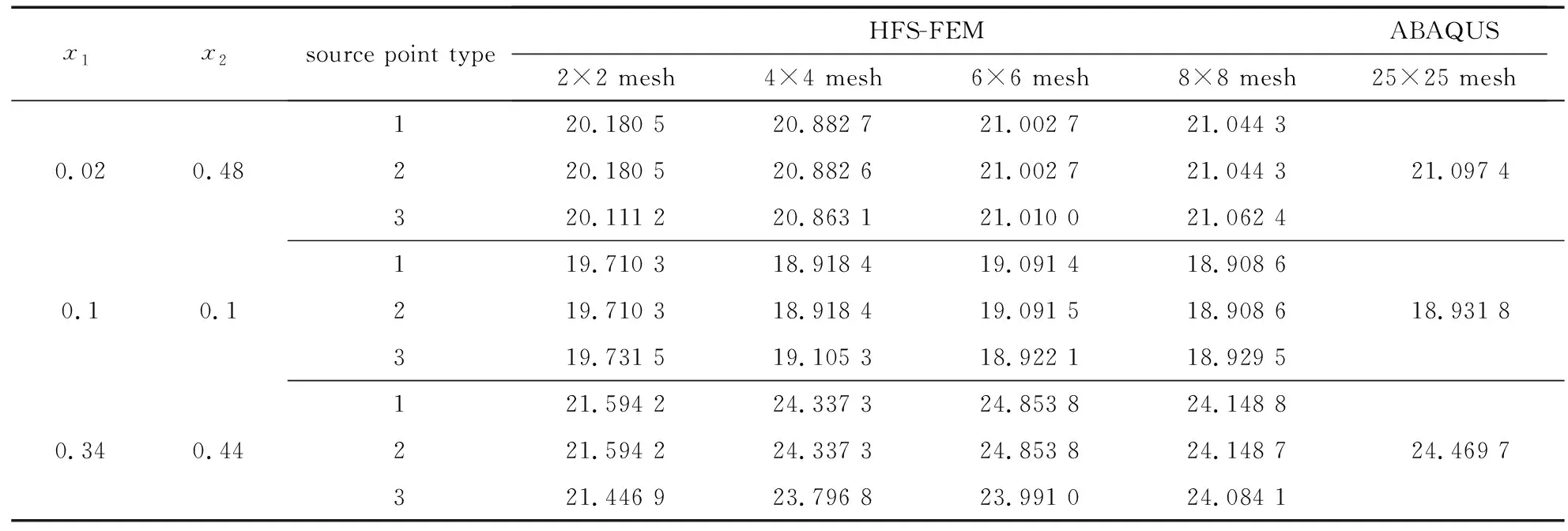
3.2 偏心環空的熱傳導

4 結 論

