一類格競爭系統(tǒng)的雙穩(wěn)周期行波解*
李 儉
(西安電子科技大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院, 西安 710071)
0 引 言
本文主要研究下面的格競爭系統(tǒng)雙穩(wěn)周期行波解的存在性:
(1)
其中uj(t),vj(t)表示u,v兩個物種在t時刻、位置j處的種群密度,d1,d2分別是物種u,v的擴(kuò)散系數(shù),ri(t)是種群內(nèi)的內(nèi)稟增長率,bi(t)是兩種群之間的競爭系數(shù),ai(t)表示種群自身的死亡率.ri(t),ai(t),bi(t)(i=1,2)∈C2()且為T-周期函數(shù),即?t>0,ri(t+T)=ri(t),ai(t+T)=ai(t),bi(t+T)=bi(t), 此外,di>0,ai(t)>0,bi(t)>0,?t∈[0,T].
系統(tǒng)(1)為下面時間周期Lotka-Volterra競爭擴(kuò)散系統(tǒng)的空間離散形式:
目前,有關(guān)Lotka-Volterra競爭系統(tǒng)行波解的研究已經(jīng)越來越廣泛.Bao和Wang在文獻(xiàn)[1]中研究了時間周期Lotka-Volterra競爭系統(tǒng)雙穩(wěn)周期行波解的存在性和穩(wěn)定性.Fang和Zhao在文獻(xiàn)[2]中研究了部分退化反應(yīng)擴(kuò)散系統(tǒng)的的單調(diào)行波解.Li在文獻(xiàn)[3]中研究了一類部分退化合作系統(tǒng)行波解的存在性.Zhao和Ruan在文獻(xiàn)[4]中研究了Lotka-Volterra競爭擴(kuò)散系統(tǒng)的時間周期行波解的存在性、唯一性和漸近穩(wěn)定性.Hao、Li和Wang在文獻(xiàn)[5]中研究了Lotka-Volterra 競爭系統(tǒng)空間周期的整體解和傳播動力學(xué).Bao、Li和Wang在文獻(xiàn)[6]中研究了Lotka-Volterra競爭擴(kuò)散系統(tǒng)的時間周期行波解的漸進(jìn)行為.在實際生活中,種群的活動空間通常是不連續(xù)的,因此考慮空間離散模型對生物種群動力學(xué)的研究具有重要的實際意義,同時,離散化后形成的格微分方程具有更豐富的動力學(xué)行為.Guo和Wu在文獻(xiàn)[7-8]中分別討論了自治情形下Lotka-Volterra格競爭系統(tǒng)的單穩(wěn)和雙穩(wěn)行波解的存在性和單調(diào)性.Wang和Ou在文獻(xiàn)[9]中討論了Lotka-Volterra格競爭系統(tǒng)的傳播方向和波速符號.Shen在文獻(xiàn)[10]中討論了二維格反應(yīng)擴(kuò)散方程雙穩(wěn)周期行波解的存在性與唯一性.考慮到物種的生存環(huán)境(例如溫度)和物種的死亡率、出生率會隨季節(jié)發(fā)生周期性改變,故在模型中加入周期.綜上,研究系統(tǒng)(1)的周期行波解對于預(yù)測物種的競爭情況有重大意義.為方便討論,給出假設(shè)條件:
(A1)(雙穩(wěn)性假設(shè))
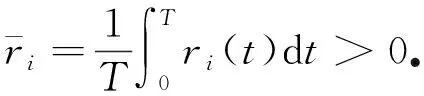
系統(tǒng)(1)所對應(yīng)的空間齊次系統(tǒng)為
(2)
在假設(shè)條件(A1)下,系統(tǒng)(2)存在4個非負(fù)的周期解(0,0),(p(t),0),(0,q(t)),(u★(t),v★(t)),此時,(p(t),0),(0,q(t))在+的內(nèi)部是穩(wěn)定的,(u★(t),v★(t))是不穩(wěn)定的.其中p(t),q(t)表示如下:
為方便討論,先做一個變換:
(3)
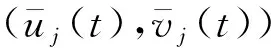
(4)
由變換(3),系統(tǒng)(1)的周期解(0,0),(0,q(t)),(p(t),0),(u★(t),v★(t))為對應(yīng)系統(tǒng)(4)的周期解(0,1),(0,0),(1,1),(u*(t),v*(t)).定義:0=(0,0),1=(1,1).因此研究系統(tǒng)(1)連接兩個穩(wěn)定半平凡平衡點的雙穩(wěn)周期行波解就轉(zhuǎn)化成了研究系統(tǒng)(4)連接兩個穩(wěn)定邊界平衡點的雙穩(wěn)周期行波解.令
下面給出周期行波解的定義.
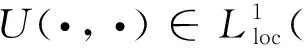
進(jìn)一步,若U(ξ,t)關(guān)于ξ∈還是單調(diào)非減的,則稱U(ξ,t)是一個周期波前解.
本文通過構(gòu)造合作系統(tǒng)(4)的上下解,并且建立比較原理,進(jìn)而證明了當(dāng)初始函數(shù)滿足一定條件時,解在無窮遠(yuǎn)處收斂,并采用黏性消去法證明了系統(tǒng)(4)連接0和1的雙穩(wěn)周期行波解的存在性.具體的思路是?D>0,構(gòu)造一個系統(tǒng)(4)的波相系統(tǒng)的輔助系統(tǒng):
(5)
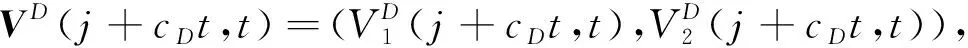
本文的剩余部分內(nèi)容如下:第1節(jié)給出了一些假設(shè)條件、重要函數(shù)及引理;第2節(jié)給出了系統(tǒng)(4)的一對上下解和比較原理;第3節(jié)利用黏性消去法證明了系統(tǒng)(4)雙穩(wěn)周期行波解的存在性;最后一節(jié)給出了本文的結(jié)論.
1 預(yù) 備 知 識
令
u=(u,v)T,f(u,t)=(f1(u,v,t),f2(u,v,t))T,Δ2[u]=u(ξ+1,t)+u(ξ-1,t)-2u(ξ,t).
假設(shè):
(H1)f:2×→2, (u,t)→f(u,t)∈C2,
(H2)f(u,t+T)=f(u,t),
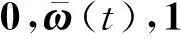
1≤i≤k},?x∈k.對于η=(η1,…,ηk),η′=(η′1,…,η′k),?1≤i≤k,若ηi≥η′i,則稱η≥η′.若ηi>η′i,則稱η?η′.若η≥η′且η≠η′,則稱η>η′.令C是k中的所有有界雙邊點序列組成的集合, 對于u=(uj)j∈,v=(vj)j∈∈C,類似上面的定義,有?j∈,若uj≥vj,則稱u≥v.若uj>vj,則稱u?v.若u≥v且u≠v,則稱u>v.任意m中的向量可認(rèn)為是m中的常數(shù)點序列, 且令

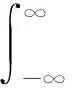
引理1 令v(x)是Kr+2ρ={x∈:|x|≤r+2ρ}(r>0,ρ>0)上的可積函數(shù),且對|Δx|≤ρ,s∈[0,r+ρ],有其中ws(·)是一個連續(xù)非減函數(shù)且ws(0)=0,則對h≤ρ,有Jr(vh,Δx)≤wr+h(|Δx|)且
證明該引理的證明可參考文獻(xiàn)[12].
2 上下解與比較原理
本節(jié)給出了系統(tǒng)(4)的上下解,建立了無界域上的比較原理,根據(jù)文獻(xiàn)[13-16],首先給出上下解的定義.
定義2 若一對連續(xù)函數(shù)(u(ξ,t),v(ξ,t))在×[0,+∞)上除了有限個點(ξi,ti),i=1,2,…,n外都是可微的,且滿足對?t≥0,ξ∈成立
(6)
則稱(u(ξ,t),v(ξ,t))是系統(tǒng)(4)的下解.通過改變不等式的方向可得系統(tǒng)上解的定義.
令
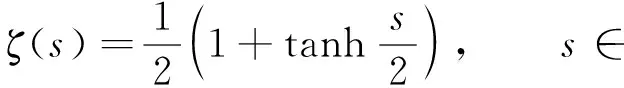
(7)
則有0<ζ(s)<1,ζ′(s)=ζ(s)(1-ζ(s)),ζ″(s)=ζ(s)(1-ζ(s))(1-2ζ(s)).因此ζ′(s)>0,|ζ″(s)|≤1,基于以上理論基礎(chǔ),給出系統(tǒng)(4)的上下解.
引理2 ?α±∈2且α-?α+,當(dāng)C充分大時,則函數(shù)
是系統(tǒng)(4)的一對上下解,其中u(t;α±)是u′(t)=f(u,t),u(0,α)=α∈2的解.
證明在該引理的證明中,僅證明v+(ξ,t)是一個上解, 下解的證明可類似得到.首先,令
則
(ui(t;α+)-ui(t;α-))(Cζ′(ξ+Ct)-diΔ2ζ(ξ+Ct))+
fi(u(t;α+),t)ζ(ξ+Ct)+fi(u(t;α-),t)(1-ζ(ξ+Ct))-
fi(u(t;α+)ζ(ξ+Ct)+u(t;α-)(1-ζ(ξ+Ct)),t).
對任意的ξ∈,t>0,由Taylor展開公式得
ζfi(u(t;α+),t)+(1-ζ)fi(u(t;α-),t)-fi(u(t;α+)ζ+u(t;α-)(1-ζ),t)=
ζ[fi(u(t;α+),t)-fi(u(t;α+)ζ+u(t;α-)(1-ζ),t)]+
(1-ζ)[fi(u(t;α-),t)-fi(u(t;α+)ζ+u(t;α-)(1-ζ),t)]-
fi(u(t;α+)ζ(ξ+Ct)+u(t;α-)(1-ζ),t)=
(uj(t;α+)-uj(t;α-))(uk(t;α+)-uk(t;α-)),
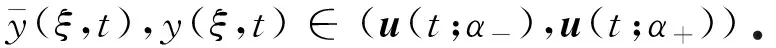
令
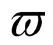
其中,z(ξ,t)∈(v(t;α-),v(t;α+)),t≥0.則
Li[v+](ξ,t)≥
故v+(ξ,t)是系統(tǒng)(4)的上解,引理得證.
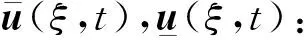
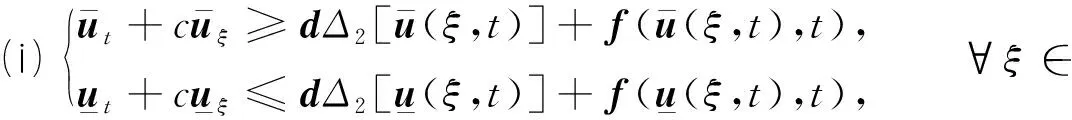
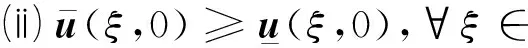
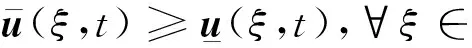
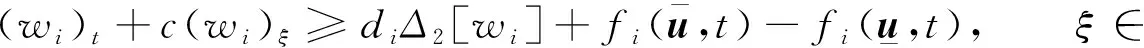
(8)
選擇充分大的K>0,滿足(7/4)K-|c|-(3/2)Lf-max{d1,d2}>0,其中
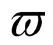
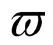
令ζ0(ξ)是一個光滑函數(shù),滿足minξ∈ζ0(ξ)=1, 當(dāng)ξ∈S,ζ0(ξ)=1, supξ∈ζ0(ξ)=ζ0(±∞)=3,
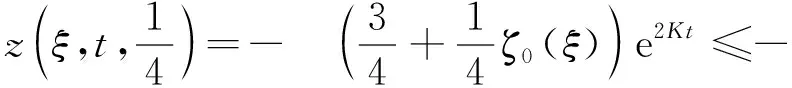

定義α*=inf{α∈(1/8,1/4]|wi(ξ,t)≥z(ξ,t,α),?ξ∈,t∈[0,t0]}.根據(jù)定義,有wi(ξ,t)≥z(ξ,t,α*),由于wi(ξ,0)≥0>z(ξ,0,α*);z(±∞,t,α*)≤-(9/8)e2Kt
[-L,L]×[0,t0]處達(dá)到最小值0,則H(ξ1,t1)=0,Ht(ξ1,t1)≤0,Hξ(ξ1,t1)=0,由式(8)且wk(ξ,t)≥0可得
0≥Ht(ξ1,t1)+cHξ(ξ1,t1)-di[H(ξ1+1,t1)+H(ξ1-1,t1)-2H(ξ1,t1)]≥
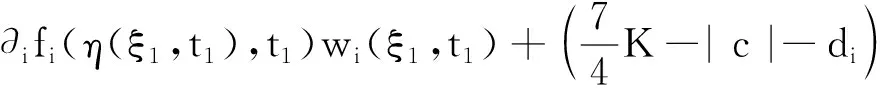
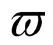
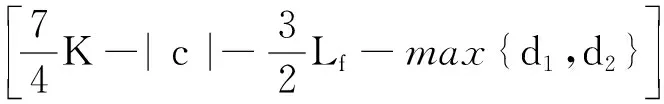
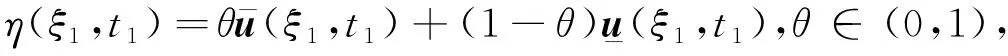
3 雙穩(wěn)周期行波解的存在性
本節(jié)利用黏性消去法證明雙穩(wěn)周期行波解的存在性,假設(shè)條件(A1)對系統(tǒng)(4)成立,在之后出現(xiàn)的定理和引理的敘述中,不再贅述.基于第2節(jié)的理論,考慮下面的輔助系統(tǒng):
(9)
根據(jù)文獻(xiàn)[11]和文獻(xiàn)[17]中的定理5.1和注5.1有:
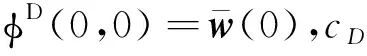
基于以上結(jié)果,下面研究{φD(ξ,t):D>0}在Lloc(2,2)中的列緊性.令VD(ξ,t)=φD(ξ,t), 則VD(ξ,t)滿足方程:
ut+cDuξ=Auξξ+dΔ2[u]+f(u,t),
(10)
其中A=(D1,D2)T.
注1 由引理3及雙穩(wěn)性假設(shè),若?ξ∈,0≤u0(ξ)≤1, 則有0≤u(ξ,t;u0)≤1;由引理4,若?ξ∈,0≤u0(ξ)≤1且u0(∞)=1,u0(-∞)=0,則u(+∞,t;u0)=1,u(-∞,t;u0)=0.
引理5 {VD(ξ,t):D>0}在Lloc(2,2)是列緊的.
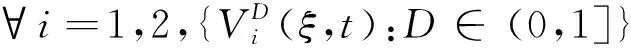
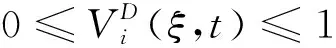
(11)
(12)
對給定的r>0,0 其中Cr是一個依賴于r的常數(shù).根據(jù)文獻(xiàn)[10]的引理2.1,?h∈(0,min{1,r/2}],有 由引理4,對D1>0,D2>0,系統(tǒng)(9)有唯一的周期行波解uD(ξ,t)=φD(ξ+cDt,t).由引理5,令Dk→0,c0∈,φ0(·,·)∈Lloc(2,2),滿足 φDk(ξ,t)→φ0(ξ,t), a.e. (ξ,t)∈×. 因此存在一個可測集E0?滿足m(E0)=0,?t∈E0,有 φDk(ξ,t)→φ0(ξ,t), a.e. (ξ,t)∈. (13) 由φD(ξ,t)關(guān)于ξ的單調(diào)性,假設(shè)0∈E0,?t∈E0,存在{Dk′}?{Dk}滿足 φDk′(ξ,t)→φ0(ξ,t), a.e. (ξ,t)∈. 由于φ0(ξ,t)關(guān)于ξ是單調(diào)的,則0≤φ0(ξ,t)≤1.?(ξ,t)∈2,令φ0(ξ+c0t,t),斷言 則有 對給定的0 由Lebesgue控制收斂定理,對任何具有緊支集的s(·)∈C∞(),有 根據(jù)Fubini定理得 基于上述理論,下面給出存在性結(jié)果. 定理1 令φ0(ξ,t)由式(13)所定義,則u±(ξ,t)=φ±(ξ+c0t,t)是系統(tǒng)(4)連接0和1的雙穩(wěn)周期行波解.其中φ±(ξ,t)=φ0(ξ±0,t). 考慮 (14) (15) φ0(ξ+c0t+0,t)=φ+(ξ+c0t,t). 則φ±(ξ,t+T)=φ±(ξ,t).下證φ0(∞,t)=1,φ0(-∞,t)=0. 由引理2可知,v+(ξ,t)是系統(tǒng)(4)的上解,由比較原理,有 v+(ξ,t)≥φ0(ξ+ct+0,t), a.e. (ξ,t)∈. 根據(jù)雙穩(wěn)假設(shè)條件,limn→∞v+(-∞,nT)=0,由于φ0(ξ±0,t)關(guān)于t是周期的,所以有φ0(-∞,0)=0.類似可證φ0(∞,0)=1,再根據(jù)注1,?t≥0,φ0(-∞,t)=0,φ0(∞,t)=1,定理證畢. 本文致力于研究格競爭系統(tǒng)的雙穩(wěn)周期行波解.首先,將非單調(diào)的競爭系統(tǒng)轉(zhuǎn)化為合作系統(tǒng),其次,建立了無界域上的比較原理,給出合作系統(tǒng)的一對上下解,最后利用黏性消去法和比較原理的方法證明格競爭系統(tǒng)連接兩個穩(wěn)定周期平衡點行波解的存在性.本文僅研究了格競爭系統(tǒng)雙穩(wěn)周期行波解的存在性,對于行波解的唯一性、穩(wěn)定性、單調(diào)性以及雙穩(wěn)行波的波速符號等問題尚未有任何結(jié)果,這將是筆者下一步需要解決的問題.
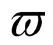
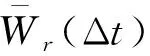
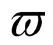
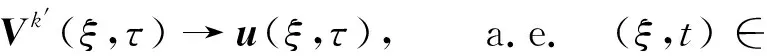
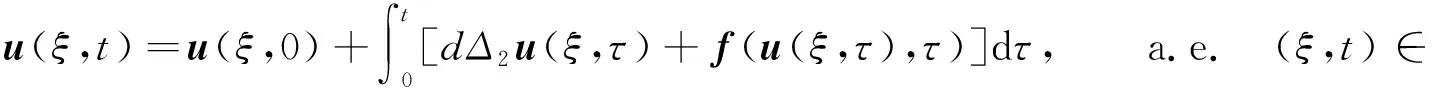
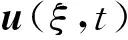
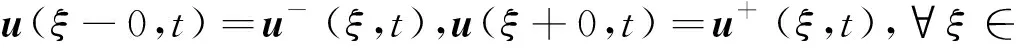
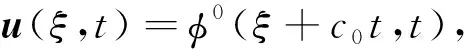
4 結(jié) 論

