基于POD-RBF方法的管道內(nèi)壁幾何識(shí)別*

余 波, 陶盈盈

(1. 合肥工業(yè)大學(xué) 土木與水利工程學(xué)院 工程力學(xué)系, 合肥 230009;2. 大連理工大學(xué) 工業(yè)裝備結(jié)構(gòu)分析國(guó)家重點(diǎn)實(shí)驗(yàn)室, 遼寧 大連 116024)

0 引 言

天然氣和石油是當(dāng)今世界上重要的化石能源,管道運(yùn)輸是其主要的運(yùn)輸方式．由于長(zhǎng)時(shí)間的運(yùn)輸,管道內(nèi)部很容易發(fā)生腐蝕老化,進(jìn)而導(dǎo)致管壁破裂和油氣泄漏等災(zāi)難性事件的發(fā)生[1]．因此,管道缺陷檢測(cè)對(duì)保證其運(yùn)輸安全尤為重要,識(shí)別管道內(nèi)壁被腐蝕的幾何形狀對(duì)精準(zhǔn)評(píng)估管道的腐蝕程度具有深刻的指導(dǎo)意義．

幾何形狀識(shí)別[2-4]主要通過(guò)系統(tǒng)外表面響應(yīng)數(shù)據(jù)進(jìn)行內(nèi)部幾何形狀估算,屬于反幾何問(wèn)題．近年來(lái),多種無(wú)損檢測(cè)技術(shù)[5-6]已被廣泛應(yīng)用于管道狀況的評(píng)估,其中漏磁檢測(cè)法[7]由于檢測(cè)范圍廣、靈敏度高、適應(yīng)性強(qiáng)以及零污染等優(yōu)勢(shì)備受關(guān)注．顯然,準(zhǔn)確快速地求解磁場(chǎng)正問(wèn)題是確保幾何形狀高效識(shí)別的前提．在眾多正問(wèn)題數(shù)值求解方法中,有限元法因其強(qiáng)大的適應(yīng)性和穩(wěn)定性,迄今為止已被廣泛地應(yīng)用于求解磁場(chǎng)問(wèn)題[8-10],并獲得了準(zhǔn)確的結(jié)果．因此,本文采用有限元法求解磁場(chǎng)的相關(guān)響應(yīng)量,并以此為基礎(chǔ)進(jìn)行管道內(nèi)壁幾何形狀的識(shí)別．

選用合適的優(yōu)化方法是反幾何問(wèn)題成功的另一關(guān)鍵點(diǎn),優(yōu)化方法可分為局部搜索的梯度類(lèi)優(yōu)化算法和全局搜索的演化類(lèi)優(yōu)化算法．由于在幾何形狀識(shí)別過(guò)程中其形狀會(huì)隨迭代過(guò)程不斷更新,從而對(duì)目標(biāo)函數(shù)靈敏度的求解帶來(lái)一定的困難,且靈敏度的求解在一定程度上會(huì)增加反演計(jì)算的成本．為避免靈敏度的計(jì)算并實(shí)現(xiàn)全局搜索的目標(biāo),本文選用非梯度類(lèi)算法進(jìn)行目標(biāo)函數(shù)的優(yōu)化．具有代表性的方法包括遺傳算法[11]、布谷鳥(niǎo)搜索算法[12]、蟻群算法[13-14]、粒子群算法[15-16]和灰狼優(yōu)化算法(grey wolf optimization, GWO)[17-18]等,其中GWO算法因其具有簡(jiǎn)單高效的優(yōu)勢(shì)而廣受學(xué)者的關(guān)注．Mirjalili等[17]提出了GWO算法并將其應(yīng)用于解決工程設(shè)計(jì)問(wèn)題．Kohli等[19]將混沌理論引入到GWO算法中,以加快其全局收斂速度．文獻(xiàn)[20]對(duì)目前GWO算法的相關(guān)改進(jìn)及應(yīng)用進(jìn)行了總結(jié),驗(yàn)證了該方法的可行性和有效性．基于此,本文選取GWO算法來(lái)實(shí)現(xiàn)管道內(nèi)壁的幾何形狀識(shí)別．

在反演迭代過(guò)程中需多次實(shí)施正問(wèn)題分析,尤其對(duì)于全局類(lèi)演化搜索算法,調(diào)用正問(wèn)題分析的次數(shù)或許可達(dá)成千上萬(wàn)次．此外,對(duì)于大型復(fù)雜模型,因其高維數(shù)和復(fù)雜性,直接進(jìn)行分析相對(duì)困難且數(shù)值模擬耗時(shí)過(guò)長(zhǎng)[21]．為此,對(duì)數(shù)值模型的規(guī)模或階數(shù)進(jìn)行有效的降階處理就顯得尤為重要．Hellstr?m等[22]利用本征正交分解法(proper orthogonal decomposition, POD)進(jìn)行了管道流動(dòng)中結(jié)構(gòu)的識(shí)別．Eftekhar Azam等[23]結(jié)合該方法和人工神經(jīng)網(wǎng)絡(luò),提出了一種監(jiān)督學(xué)習(xí)方法,并用于檢測(cè)、定位和量化結(jié)構(gòu)損傷強(qiáng)度．POD是預(yù)測(cè)響應(yīng)最受歡迎的模型降階方法之一,該方法以有限的數(shù)據(jù)捕獲計(jì)算過(guò)程中的主要成分,可顯著降低自由度,提升計(jì)算效率．但該方法的精度受樣本數(shù)量與樣本間相關(guān)性等因素的影響,樣本的選擇至關(guān)重要．利用本文建立的變幾何樣本庫(kù)可有效處理這一難題．

常規(guī)POD的預(yù)測(cè)模型隨著幾何形狀的改變需要反復(fù)更新有限元?jiǎng)偠染仃?這在一定程度上嚴(yán)重增加了POD模型的計(jì)算成本．因此,探索一種代理模型以避免在計(jì)算過(guò)程中因幾何改變反復(fù)求解有限元?jiǎng)偠染仃囀欠浅Ｓ斜匾模Ｒ?jiàn)的代理模型有多項(xiàng)式回歸(polynomial regression, PR)[24-25]、Kriging(KRG)[26-27]、徑向基函數(shù)(radial basis function, RBF)[28-30]和人工神經(jīng)網(wǎng)絡(luò)(artificial neural network, ANN)[31-32]等．其中,PR模型是通過(guò)樣本數(shù)據(jù)基于最小二乘原理來(lái)擬合近似多項(xiàng)式．由于PR的模型簡(jiǎn)單、計(jì)算量小,且多項(xiàng)式的平滑能力能使帶有噪聲的函數(shù)快速收斂,因而成為最常用的代理模型之一．然而,PR在處理高度非線性問(wèn)題時(shí),由于高次多項(xiàng)式的使用會(huì)出現(xiàn)不穩(wěn)定現(xiàn)象．KRG是對(duì)區(qū)域變量求無(wú)偏內(nèi)插估計(jì)值的一種插值方法,預(yù)測(cè)精度主要依賴(lài)于初始采樣,可能會(huì)導(dǎo)致模型過(guò)早停止或過(guò)于局部收斂．ANN是一種模擬人腦分析和處理信息方式的人工智能算法．該方法從復(fù)雜的數(shù)據(jù)中學(xué)習(xí),確定輸入和輸出變量之間的關(guān)系,從而進(jìn)行預(yù)測(cè)分析．RBF模型以關(guān)于Euclidean距離或者其他類(lèi)似度量的函數(shù)為基函數(shù)[33-34],通過(guò)線性加權(quán)來(lái)插值擬合數(shù)據(jù)．Jin等[35]利用多種性能評(píng)價(jià)標(biāo)準(zhǔn)和14個(gè)標(biāo)準(zhǔn)測(cè)試函數(shù)系統(tǒng)地比較研究了PR、RBF和KRG等代理模型的性能,得出在處理不同階數(shù)的非線性和問(wèn)題規(guī)模時(shí),RBF模型在準(zhǔn)確性和穩(wěn)定性等方面的表現(xiàn)最好．Jing等[36]提出了一種基于自適應(yīng)RBF與遺傳算法相結(jié)合的可靠性評(píng)估方法,以降低結(jié)構(gòu)可靠性分析的計(jì)算成本．Liu等[37]針對(duì)多目標(biāo)優(yōu)化計(jì)算量大的問(wèn)題,利用RBF提出一種基于自適應(yīng)逼近模型的高效多目標(biāo)優(yōu)化方法,并通過(guò)算例驗(yàn)證了該方法的有效性和實(shí)用性．綜上,若將POD和RBF的優(yōu)勢(shì)耦合,即可實(shí)現(xiàn)在降階分析正問(wèn)題的同時(shí)避免剛度矩陣的重復(fù)計(jì)算．例如,Khatir等[38]基于擴(kuò)展等幾何分析,將斷裂力學(xué)試驗(yàn)與數(shù)值模型相結(jié)合,利用POD-RBF識(shí)別了板結(jié)構(gòu)的單、多裂紋．Henneron等[39]應(yīng)用該方法能夠在合理的計(jì)算時(shí)間和良好的精度下得到有限元的近似解,從而模擬非線性靜磁器件．Wang等[40]基于仿真結(jié)果,采用POD-RBF的降階方法,預(yù)測(cè)了不同滑移幅值和不同微動(dòng)磨損循環(huán)次數(shù)下試樣的磨損特性．研究表明,POD-RBF可高效準(zhǔn)確地預(yù)測(cè)相關(guān)響應(yīng)量,顯著地降低計(jì)算成本．截至目前,已出版的研究工作基本上是基于固定幾何樣本庫(kù)采用POD-RBF進(jìn)行響應(yīng)量的預(yù)測(cè)．為此,本文基于構(gòu)建的變幾何樣本庫(kù)建立了POD-RBF降階代理模型．該方法可期望在識(shí)別過(guò)程中避免因管道內(nèi)壁幾何形狀的改變而需反復(fù)求解剛度矩陣,在滿(mǎn)足擬合精度要求的前提下降低計(jì)算成本．

1 管道內(nèi)部幾何反演理論

1.1 靜磁場(chǎng)二維有限元基本理論

本文在靜磁場(chǎng)環(huán)境中進(jìn)行管道內(nèi)壁幾何形狀的識(shí)別,將其簡(jiǎn)化為平面問(wèn)題,對(duì)應(yīng)的平衡方程為[41]

(1)

其中x=(x,y),μr為相對(duì)磁導(dǎo)率,μ0為空氣磁導(dǎo)率,Az為磁勢(shì),Jz為電流密度．

考慮兩類(lèi)邊界條件:

(2)

如圖1所示,Γ=Γ1∪Γ2表示域Ω的邊界,m,n分別是Γ2和Γd的法向單位矢量,Bt為切向磁通密度．

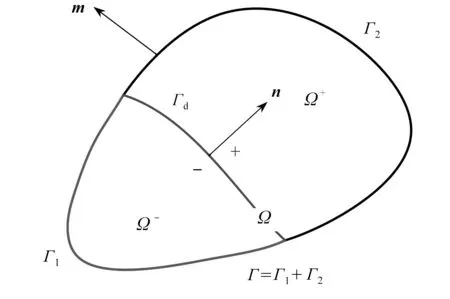
圖1 求解域示意圖Fig. 1 The diagram of the solution domain

在磁導(dǎo)率不同的兩種媒質(zhì)界面Γd上,磁勢(shì)應(yīng)滿(mǎn)足連續(xù)性條件:

(3)

對(duì)式(1)應(yīng)用Galerkin有限元法可得

(4)

通過(guò)有限元離散可得

KAz=Jz,

(5)

其中K為總體剛度矩陣,Az為結(jié)點(diǎn)磁勢(shì)向量,Jz為電流載荷向量．

不同管道內(nèi)壁幾何對(duì)應(yīng)模型不同的表面磁勢(shì)信息,其中管道內(nèi)壁幾何由若干個(gè)幾何參數(shù)表示．在管道內(nèi)壁識(shí)別過(guò)程中,通過(guò)有限元計(jì)算獲得不同管道內(nèi)壁幾何相應(yīng)的磁勢(shì)信息,進(jìn)而生成樣本,并建立磁勢(shì)數(shù)據(jù)與幾何參數(shù)的關(guān)系．另外,利用管道內(nèi)壁真實(shí)幾何模型的磁勢(shì)信息,對(duì)管道內(nèi)壁幾何形狀進(jìn)行預(yù)測(cè)．

1.2 本征正交分解-徑向基函數(shù)

在采用POD-RBF求解之前,建立有效的樣本庫(kù)關(guān)系到問(wèn)題的求解精度,因此選取合適的樣本點(diǎn)至關(guān)重要．拉丁超立方抽樣(Latin hypercube sampling, LHS)方法是目前使用較為廣泛的抽樣方法之一,該抽樣方法利用分層的思想,保證樣本點(diǎn)是從給定的設(shè)計(jì)空間內(nèi)均勻隨機(jī)抽取的．基于LHS生成POD-RBF降階代理模型所需樣本庫(kù)的參數(shù),有效避免了計(jì)算過(guò)程中因管道內(nèi)壁幾何形狀改變反復(fù)更新剛度矩陣,能在保證計(jì)算精度的同時(shí)提高計(jì)算效率．

絕大部分工作均選用某個(gè)方向上的磁感應(yīng)強(qiáng)度進(jìn)行研究,我們期望從數(shù)值上建立全面反應(yīng)有關(guān)磁感應(yīng)強(qiáng)度信息的數(shù)據(jù)與模型幾何的關(guān)系,故選用有限元分析中的磁勢(shì)作為響應(yīng)量．在相同邊界條件下,通過(guò)LHS生成對(duì)應(yīng)的不同管道內(nèi)壁幾何參數(shù),進(jìn)而利用有限元計(jì)算得到磁勢(shì)樣本矩陣:

ψ=[ζ(α1),ζ(α2),ζ(α3),…,ζ(αN)],

(6)

式中αi為控制管道內(nèi)壁幾何的參數(shù),ζ(αi)為n維磁勢(shì)列向量,N表示樣本個(gè)數(shù)．

對(duì)樣本矩陣ψ進(jìn)行奇異值分解:

ψ=CSVT,

(7)

式中C∈Rn×n為ψ的左奇異向量組成的矩陣;V∈RN×N為ψ的右奇異向量組成的矩陣;S∈Rn×N僅在主對(duì)角線上有值,稱(chēng)為ψ的奇異值,可表示為si(i=1,2,…,min(n,N))．所有奇異值按降序排列,通過(guò)以下規(guī)則

(8)

實(shí)現(xiàn)k個(gè)奇異值和對(duì)應(yīng)奇異向量的自適應(yīng)截?cái)噙M(jìn)而可近似描述矩陣ψ,即

(9)

本文χ取99.999%．

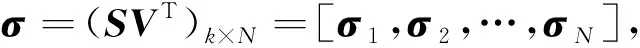
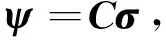
(10)

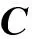
(11)

其中i=1,2,…,N;q=1,2,…,k．

寫(xiě)成矩陣形式為

σ=WΦ,

(12)

其中W為wqj組成的矩陣,Φ可表示為

(13)

為了提升計(jì)算效率這里選用inverse multiquadtric(InvM)核函數(shù)對(duì)Φ進(jìn)行近似展開(kāi),則Φ中任一元素φj(αi)可表示為

(14)

式中,c是取值大于零的平滑系數(shù),rji表達(dá)式如下:

rji=‖αi-αj‖2,

(15)

‖αi‖2為αi的2范數(shù)．由式(12)可得

W=σΦ-1．

(16)

通過(guò)式(10)、(12)、(16)可得任意參數(shù)αp對(duì)應(yīng)的磁勢(shì)響應(yīng)量:

(17)

由式(17)可以看出,通過(guò)變幾何樣本庫(kù)的構(gòu)建,在求解不同管道內(nèi)壁幾何對(duì)應(yīng)磁勢(shì)響應(yīng)量時(shí),只需更新幾何對(duì)應(yīng)的基函數(shù)向量Φ(αp),這將在很大程度上節(jié)省計(jì)算成本．

1.3 目標(biāo)函數(shù)的優(yōu)化

通過(guò)確定管道內(nèi)壁幾何參數(shù)αp即可確定管壁的幾何形狀,建立與αp有關(guān)的目標(biāo)函數(shù)

(18)

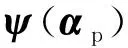
受灰狼群體捕食行為的啟發(fā),GWO算法被提出．灰狼被認(rèn)為是食物鏈頂端的捕食者,大部分喜歡群居,一個(gè)群體平均有5～12只狼．在群體中,他們有著嚴(yán)格的等級(jí)制度,如圖2所示,從高到底依次是首領(lǐng)狼a,副首領(lǐng)狼b,普通狼c和底層狼ω．

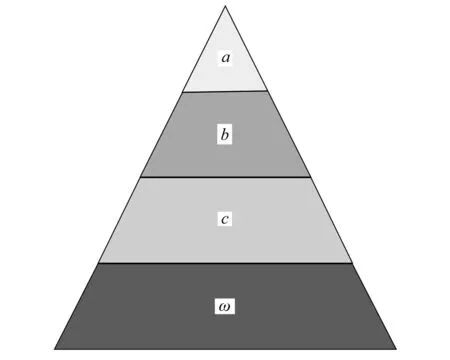
圖2 灰狼的等級(jí)制度Fig. 2 The hierarchy of gray wolves

灰狼的狩獵是在首領(lǐng)狼a的帶領(lǐng)下,進(jìn)行圍攻捕食．捕食過(guò)程分為三個(gè)階段:

1) 通過(guò)氣味跟蹤、追逐、接近獵物;

2) 鎖定獵物位置后,進(jìn)行包圍;

3) 快速地攻擊獵物．

在狼群捕食過(guò)程中,圍剿獵物公式為

C=|CXp(t)-X(t)|,

(19)

C=2?1,

(20)

式中Xp(t)為獵物的位置,t是迭代步數(shù),X(t)為灰狼的位置,?1從[0,1]范圍內(nèi)隨機(jī)取值．灰狼的位置更新如下:

X(t+1)=Xp(t)-BD,

(21)

在更新過(guò)程中,保留當(dāng)前結(jié)果最好的前三組解,依次為a,b和c狼的位置．狼群中其他狼的位置根據(jù)a,b和c狼的位置進(jìn)行更新:

(22)

(23)

通過(guò)式(22)、(23)不斷更新前三個(gè)最優(yōu)灰狼的位置,直到滿(mǎn)足優(yōu)化標(biāo)準(zhǔn)條件．

2 數(shù) 值 算 例

2.1 基于POD-RBF對(duì)響應(yīng)量的預(yù)測(cè)

取管道任一橫截面的附近區(qū)域進(jìn)行分析,假定待識(shí)別的管道內(nèi)壁幾何分別為圓、橢圓和不規(guī)則形狀．圖3是該問(wèn)題的簡(jiǎn)化模型,幾何尺寸如圖所示,其中方塊被選為參考點(diǎn)(即后續(xù)算例中的測(cè)點(diǎn)),區(qū)域Ι、Ⅱ和Ⅲ分別為石油(或天然氣)、管道壁和空氣．在正方形上邊界(y=1)處施加磁勢(shì)Az=0.5 Wb/m,下邊界(y=-1)處施加Az=0 Wb/m．天然氣和石油由于抗磁性它們的相對(duì)磁導(dǎo)率和空氣相近,即相對(duì)磁導(dǎo)率μr均取為1．管道材料選用常用的X52鋼,對(duì)應(yīng)的B-H取值參考文獻(xiàn)[42]．

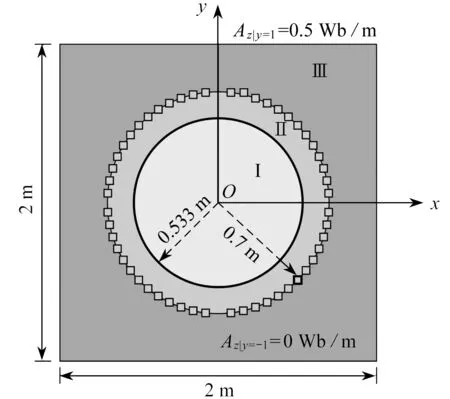
圖3 圓型管道內(nèi)壁Fig. 3 The inner wall of the circular pipeline

首先對(duì)POD-RBF模型的正確性進(jìn)行驗(yàn)證,假定管道內(nèi)壁形狀為圓,該幾何對(duì)應(yīng)的參數(shù)αp里僅有一個(gè)元素,其值為0.533 m．樣本對(duì)應(yīng)的參數(shù)α通過(guò)LHS在0.5～0.6 m生成10組．用POD-RBF模型預(yù)測(cè)被對(duì)比點(diǎn)的磁勢(shì)．有限元計(jì)算采用9 856個(gè)四節(jié)點(diǎn)四邊形單元,10 037個(gè)節(jié)點(diǎn),單元?jiǎng)澐秩鐖D4所示,圖5展示了相應(yīng)磁場(chǎng)強(qiáng)度的大小．兩種方法計(jì)算結(jié)果誤差如圖6所示．

圖6(b)顯示POD-RBF計(jì)算預(yù)測(cè)的響應(yīng)量與有限元計(jì)算結(jié)果的最大相對(duì)誤差不超過(guò)0.06%,即該算法對(duì)求解管道內(nèi)部?jī)?nèi)壁幾何正問(wèn)題有效．

圖4 有限元網(wǎng)格 圖5 磁場(chǎng)強(qiáng)度大小Fig. 4 The FEM meshFig. 5 The magnetic field intensity

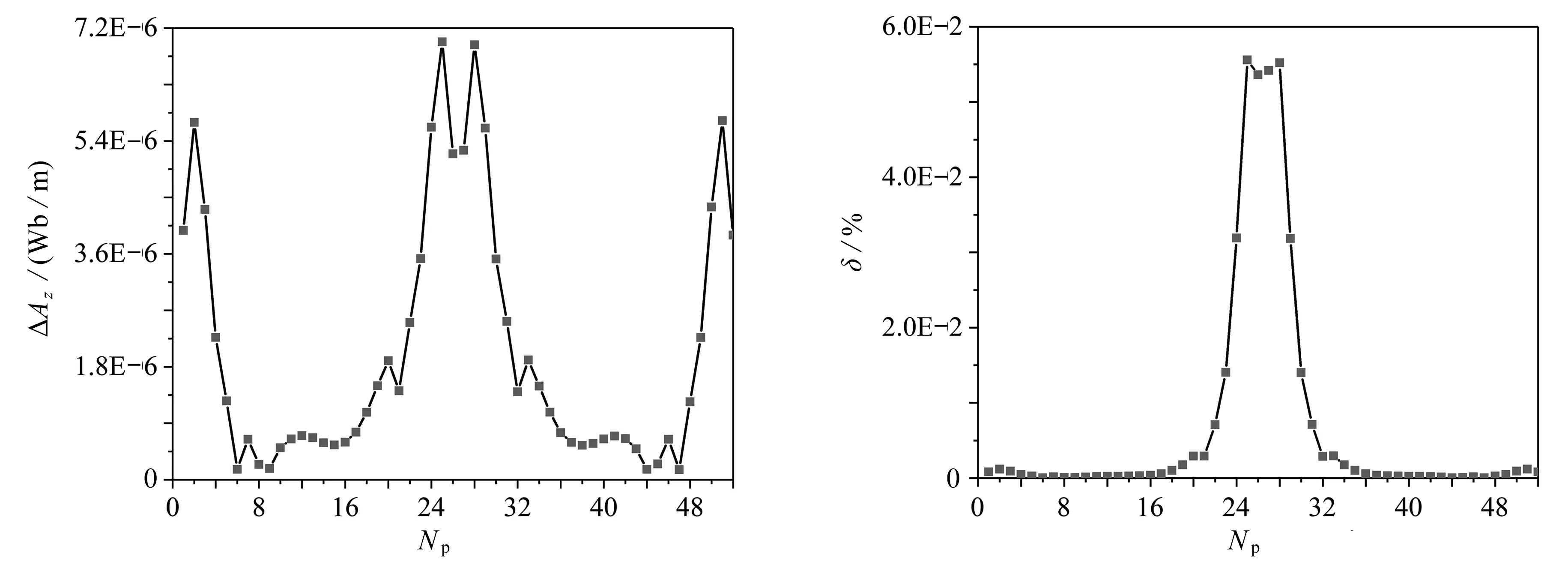
(a) 參考點(diǎn)磁勢(shì)的絕對(duì)誤差 (b) 參考點(diǎn)磁勢(shì)的相對(duì)誤差(a) Absolute errors of the magnetic potential at the reference points(b) Relative errors of the magnetic potential at the reference points圖6 參考點(diǎn)磁勢(shì)的誤差Fig. 6 The magnetic potential errors at the reference points

2.2 不同樣本數(shù)量對(duì)識(shí)別結(jié)果的影響

本小節(jié)對(duì)如圖3所示管道內(nèi)壁幾何為圓的問(wèn)題進(jìn)行反演．利用LHS在0.5～0.6 m分別生成10組、20組和40組相應(yīng)的幾何參數(shù)α,再通過(guò)有限元分別建立N=10,20,40的樣本庫(kù),進(jìn)一步探究不同樣本數(shù)量對(duì)反演結(jié)果的影響．

ε和tmax分別設(shè)定為10-10和100．從表 1對(duì)比分析的三組樣本方案結(jié)果顯示,不同數(shù)量的樣本均能達(dá)到較高的識(shí)別精度．如圖7和圖8所示,當(dāng)管道內(nèi)壁形狀為圓時(shí),采用不同數(shù)量的樣本,識(shí)別結(jié)果均在16步內(nèi)收斂．使用40組樣本時(shí),經(jīng)過(guò)6次迭代即可獲得更準(zhǔn)確的識(shí)別結(jié)果,但計(jì)算成本可能會(huì)隨著樣本數(shù)量的增加而增大．因此在復(fù)雜模型識(shí)別中,選擇合適數(shù)量的樣本至關(guān)重要．

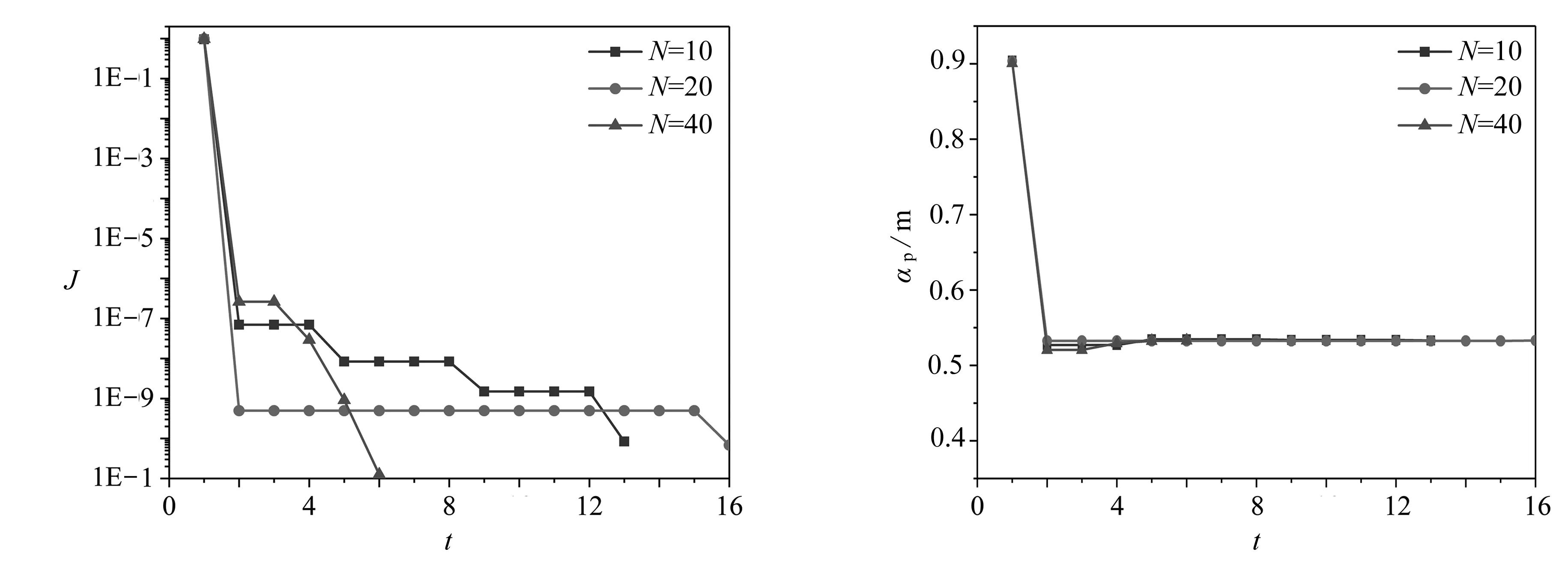
圖7 不同樣本數(shù)量對(duì)應(yīng)的目標(biāo)函數(shù)值 圖8 不同樣本數(shù)量對(duì)應(yīng)的幾何參數(shù) Fig. 7 Objective function values with different sample sizes Fig. 8 Geometric parameters with different sample sizes

表1 識(shí)別結(jié)果

為了確定后續(xù)算例的樣本,采用繼承LHS[43]生成樣本,期望在保證精度的同時(shí)盡可能降低計(jì)算成本．經(jīng)測(cè)試,后續(xù)分別擬采用50組和40組樣本進(jìn)行橢圓形和不規(guī)則形內(nèi)壁幾何的識(shí)別．

同時(shí)樣本中對(duì)應(yīng)的幾何參數(shù)范圍也會(huì)影響識(shí)別結(jié)果,接下來(lái)我們討論在當(dāng)前樣本N=10下管壁幾何的識(shí)別情況．待識(shí)別的真實(shí)管壁幾何半徑在0.45～0.69 m內(nèi),識(shí)別結(jié)果如表 2所示．

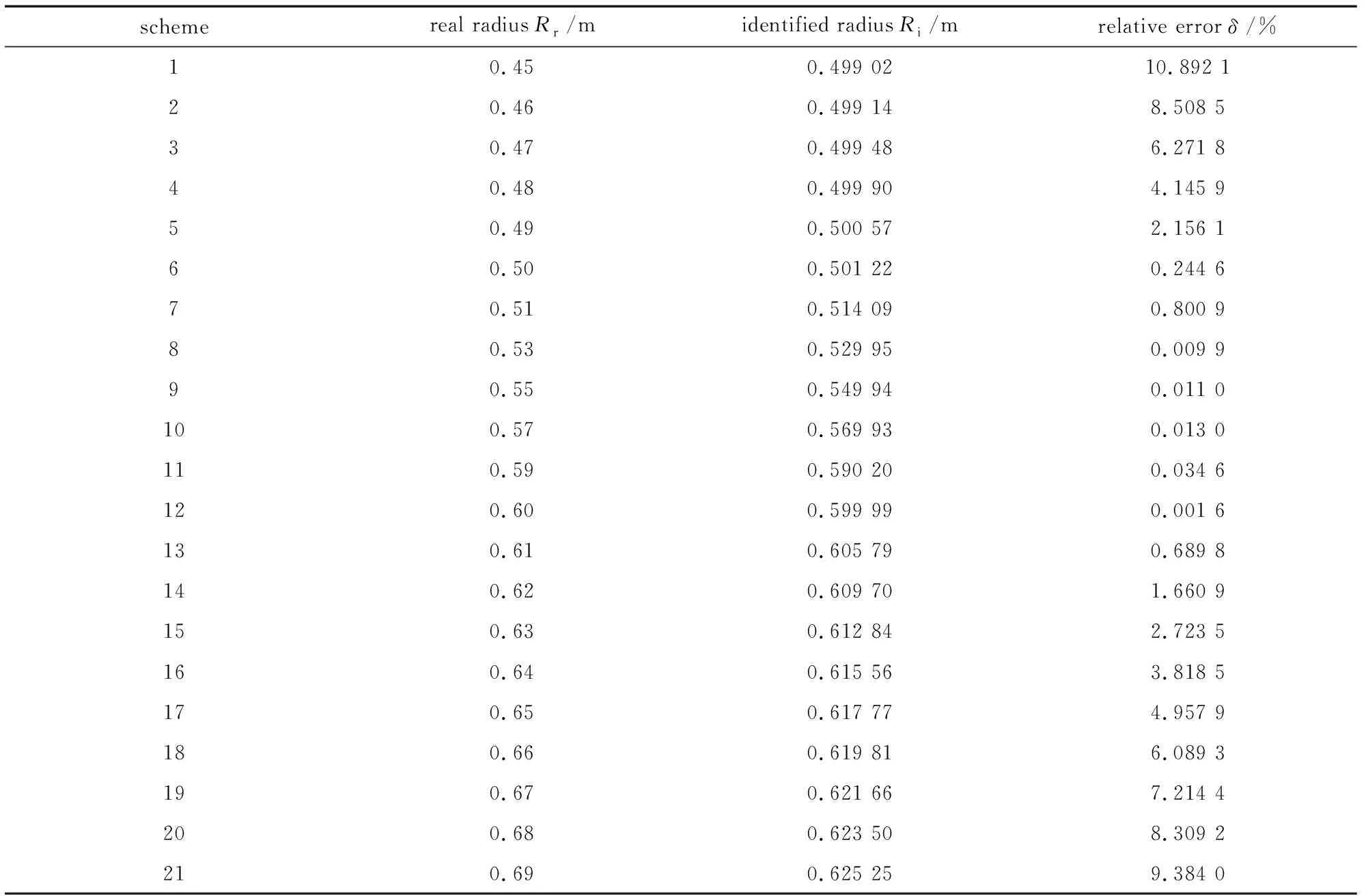
表2 不同方案下的識(shí)別結(jié)果

從表中可知,真實(shí)內(nèi)壁幾何在0.50～0.61 m間識(shí)別結(jié)果的相對(duì)誤差均在1%內(nèi),在這范圍外的相對(duì)誤差隨著半徑的增大(或減小)而增加,當(dāng)半徑減小到0.45 m時(shí),識(shí)別結(jié)果的相對(duì)誤差達(dá)到了10.892 1%．綜上,在有限的樣本下,待識(shí)別的幾何參數(shù)在所建立樣本庫(kù)相應(yīng)的幾何參數(shù)范圍內(nèi)識(shí)別結(jié)果更準(zhǔn)確．但當(dāng)樣本庫(kù)足夠大時(shí),理論上可以識(shí)別出任意管壁的幾何．

2.3 基函數(shù)對(duì)反演結(jié)果的影響

如圖9所示,本小節(jié)假定管道內(nèi)壁形狀為橢圓,真實(shí)幾何對(duì)應(yīng)的參數(shù)αp=[0.625,0.42]Tm．通過(guò)InvM核函數(shù)和緊支撐的四階樣條函數(shù)[44]討論不同基函數(shù)對(duì)識(shí)別結(jié)果的影響．其中緊支撐的四階樣條函數(shù)可以表示為

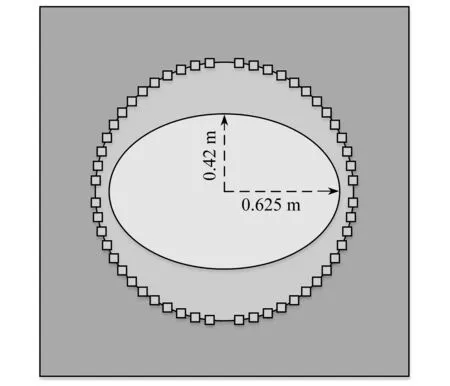
圖9 橢圓型管道內(nèi)壁Fig. 9 The inner wall of the elliptical pipeline

(24)

樣本對(duì)應(yīng)的參數(shù)α由LHS在0.40～0.65 m生成50組．ε和tmax分別設(shè)定為10-8和300,兩種方法的迭代初始值均設(shè)置在0.9～1.0 m之間．

如圖10所示,使用緊支撐的四階樣條函數(shù)迭代總次數(shù)少于InvM核函數(shù),且兩種方法均能得到比較準(zhǔn)確的幾何．但在同樣的步數(shù)下,InvM核函數(shù)耗時(shí)更短．同時(shí)為兼顧反演成本,在后續(xù)算例中選用InvM核函數(shù)．

(a) Inverse multiquadtric核函數(shù)(a) Inverse multiquadtric kernel functions

2.4 不同誤差對(duì)反演結(jié)果的影響

為驗(yàn)證本文方法的抗噪性,本小節(jié)在測(cè)點(diǎn)響應(yīng)上添加隨機(jī)誤差．算例采用如圖11所示的模型,管道內(nèi)壁的幾何形狀由12個(gè)參數(shù)控制,該組參數(shù)在平面內(nèi)均勻分布,從0°～360°每隔θ=30°選取,最后通過(guò)樣條曲線擬合成封閉圖形．樣本對(duì)應(yīng)的參數(shù)α由LHS在0.5～0.6 m內(nèi)生成40組, 真實(shí)幾何對(duì)應(yīng)的參數(shù)αp=[0.526,0.578,0.533,0.556,0.518,0.544,0.538,0.575,0.510,0.565,0.530,0.594]Tm．

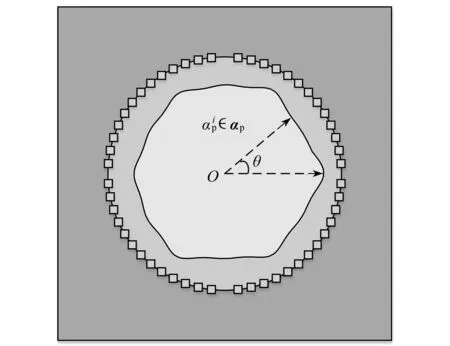
圖11 不規(guī)則幾何形狀的管道內(nèi)壁Fig. 11 The inner wall of the pipeline with irregular geometry

考慮1%,2%和3%的隨機(jī)誤差,添加誤差后的測(cè)點(diǎn)磁勢(shì)可表示為

(25)

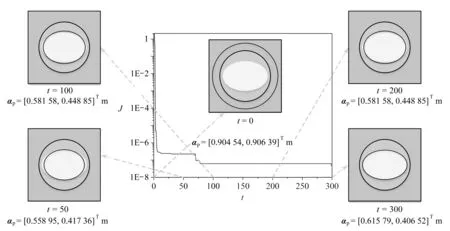
本算例假定ε和tmax分別為10-7和8 000．需要說(shuō)明的是,有限元模型與POD-RBF降階代理模型的計(jì)算結(jié)果是存在一定偏差的．

表 3列出了在不同誤差水平下的參數(shù)識(shí)別結(jié)果．

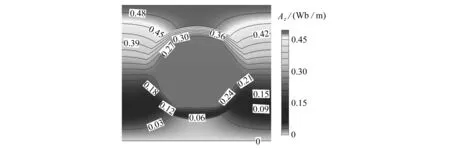
圖12直接展現(xiàn)了本文方法識(shí)別帶有12個(gè)幾何參數(shù)問(wèn)題的性能．值得注意的是,在δ=0時(shí),識(shí)別出的幾何參數(shù)與真實(shí)參數(shù)存在微小差異,但擬合出的邊界與真實(shí)邊界幾乎完全重合．從圖13和圖14可以看到,在誤差水平分別為1%和2%時(shí),識(shí)別結(jié)果與真實(shí)幾何仍吻合較好．甚至δ=3%時(shí),圖15顯示本文方法仍能識(shí)別出幾何的基本輪廓．另外,從圖16更能直觀地觀察到,在不同的誤差水平下,本文方法可獲得較為理想的磁勢(shì)響應(yīng)場(chǎng)和識(shí)別結(jié)果．

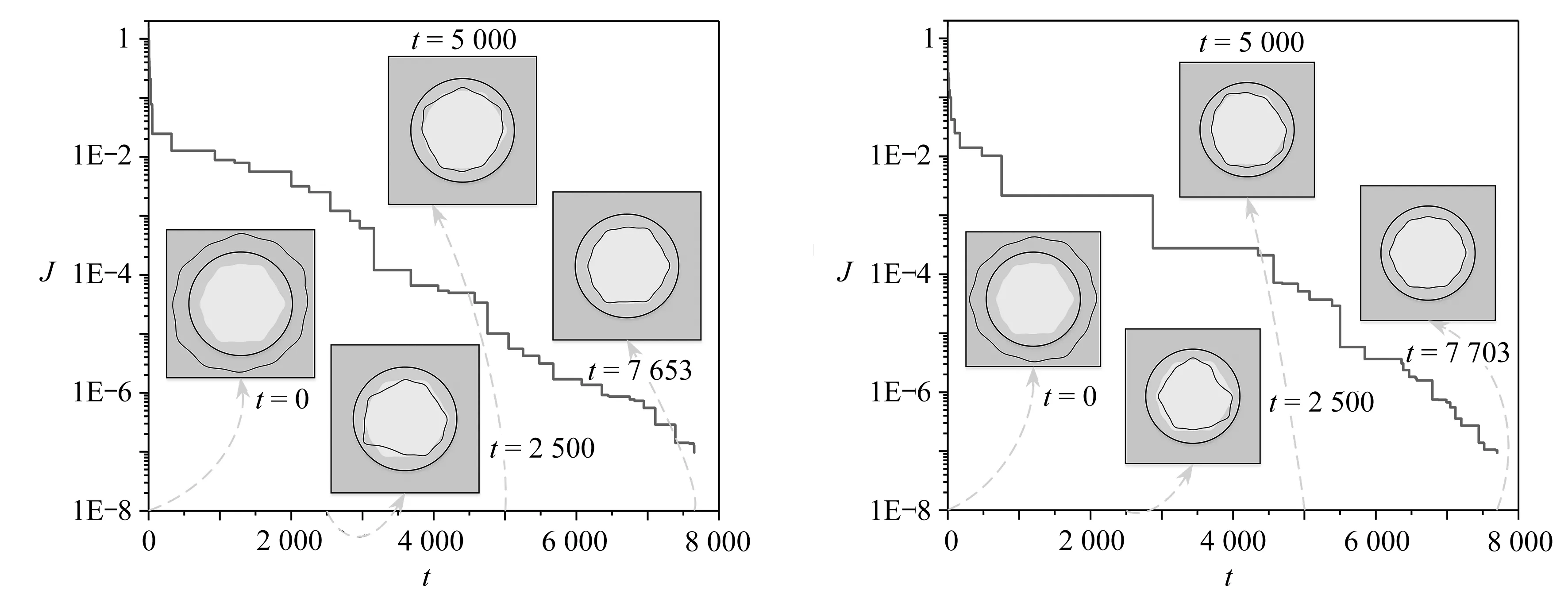
圖12 δ=0時(shí)的識(shí)別結(jié)果 圖13 δ=1%時(shí)的識(shí)別結(jié)果 Fig. 12 The identified results with δ=0Fig. 13 The identified results with δ=1%

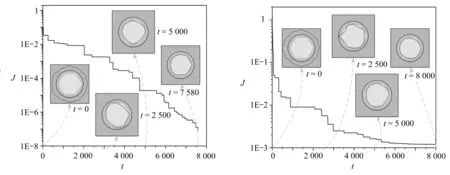
圖14 δ=2%時(shí)的識(shí)別結(jié)果 圖15 δ=3%時(shí)的識(shí)別結(jié)果 Fig. 14 The identified results with δ=2%Fig. 15 The identified results with δ=3%

(a) 真實(shí)幾何 (a) The true geometry

3 結(jié) 論

本文建立了變幾何樣本庫(kù)的POD-RBF降階代理模型,結(jié)合GWO算法構(gòu)建了一種新型的管道內(nèi)壁幾何識(shí)別框架．通過(guò)LHS生成樣本庫(kù)后,利用POD-RBF對(duì)響應(yīng)量進(jìn)行預(yù)測(cè),可避免迭代過(guò)程中因幾何改變而反復(fù)更新剛度矩陣．GWO算法的引入實(shí)現(xiàn)了無(wú)需靈敏度計(jì)算的全局目標(biāo)函數(shù)優(yōu)化．?dāng)?shù)值算例表明,本文算法不僅能夠準(zhǔn)確預(yù)測(cè)正問(wèn)題響應(yīng),同時(shí)可實(shí)現(xiàn)對(duì)管道內(nèi)壁幾何的準(zhǔn)確識(shí)別．即使對(duì)于帶有高維幾何參數(shù)且考慮噪聲問(wèn)題,該算法仍具備強(qiáng)勁的識(shí)別性能,顯示出了良好的識(shí)別穩(wěn)定性．同時(shí),本文的研究工作可為拓?fù)鋬?yōu)化、幾何識(shí)別和無(wú)損檢測(cè)等變幾何計(jì)算問(wèn)題提供新思路．

致謝本文作者衷心感謝工業(yè)裝備結(jié)構(gòu)分析國(guó)家重點(diǎn)實(shí)驗(yàn)室開(kāi)放基金(GZ21109)對(duì)本文的資助．