基于響應差的老舊連續梁橋損傷判定研究

周成亮

（山東高速工程建設集團有限公司，山東 濟南 250000）

0 引言

荷載不均、環境侵蝕、設計不規范以及車輛超載等很多因素都可能造成橋梁損傷，而損傷是否影響橋梁正常使用是人們關注的重點，因此橋梁的損傷判定成為研究的熱點，尤其是部分臨近年限仍在服役且處于關鍵位置的連續梁橋。

國內外學者對橋梁橋損傷檢測進行了大量研究，但多為針對擁有健康檢測數據的橋梁，較少針對缺乏完整狀態數據的老舊橋梁，較少考慮如橋梁跨徑、橋梁剛度等對老舊橋梁影響較嚴重的因素，因此判定結果存在一定程度的誤差。基于此，該文針對需要改建的老舊連續梁橋狀態數據不全問題，提出了一種基于響應差的連續梁橋損傷判定方法，并通過模擬多種損傷情況來驗證方法的有效性。

1 基于響應差的損傷位置識別方法

一般服役時間較長的老舊橋梁狀態數據資料較欠缺，因此需要一種不過多借助數據就可識別損傷位置的方法。車輛經過損傷位置時，僅改變牽引車配重，撓度變化量在損傷位置就會出現細微突變，而撓度的突變必然引起加速度響應差的敏感變化，對響應差進行離散小波變換，再對小波變換系數處理就可間接識別損傷位置[1-2]，基于此，該文提出了一種損傷位置識別方法。

1.1 橋梁響應差模型參數

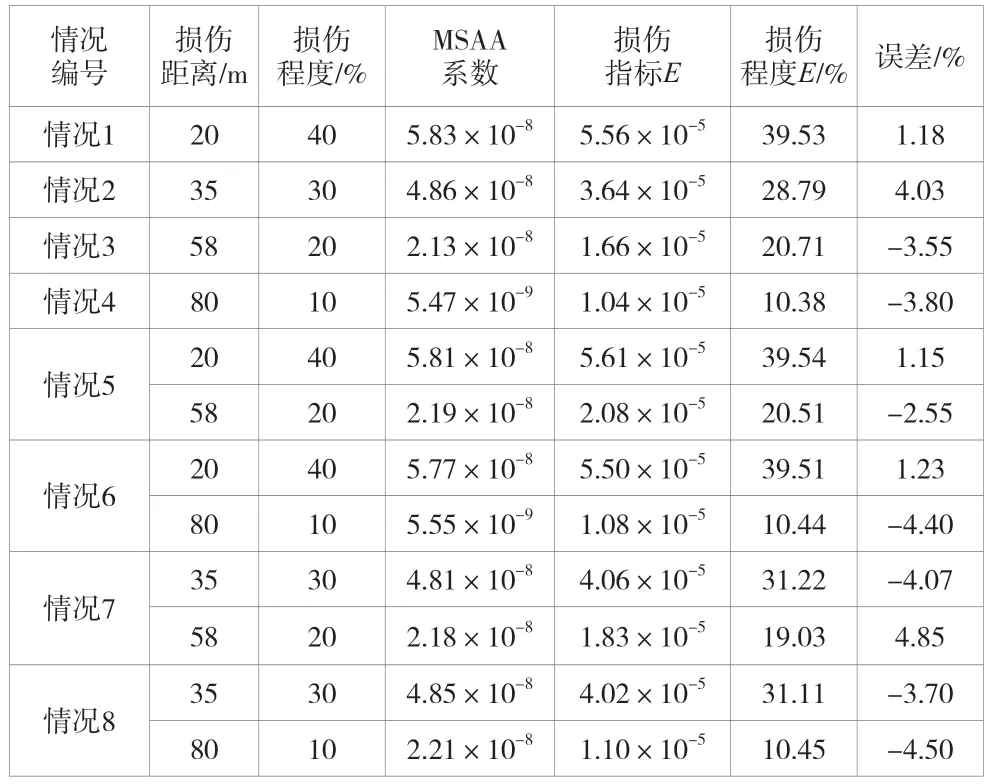
假設牽引車力分別為F1和F2且F1

圖1 車輛過損傷位置橋梁示意圖

2 次行駛過程中檢測車位置處的撓度f1（x）和f2（x）如公式（1）、公式（2）所示，檢測車體加速度響應w1和w2如公式（3）、公式（4）所示。

式中：EI為梁的彎曲撓度；l為路段長度；x為損傷位置距左側位置；Fc為檢測車力；?a為牽引車與檢測車質心距離，其中a1～a3、b1～b7、c1皆為計算加速度響應所需參數[3]。

1.2 橋梁橋損傷位置識別

對公式（3）和公式（4）進行離散小波變換，并將未損傷位置和損傷位置加以區分，得到車輛的加速度響應差?w，如公式（5）所示。

式中：θd為區分損傷位置和未損傷位置設立的離散小波變換參數，根據實際情況取值，通過該參數來表達損傷程度；H（x）為做差后的偏差[4]。

由公式（5）可知，損傷位置的加速度響應差和未損傷位置相比存在突變，表明利用離散小波變化可以識別連續梁橋的損傷位置且對小波變換系數進行極大值逐次逼近（Maximum Successive Approximation Approach，MSAA）處理后，可進一步提升損傷位置識別的準確性。

2 橋梁損傷程度判定

已知MSAA 系數可有效幫助識別橋梁損傷位置且MSAA系數存在一定規律性，與損傷程度之間存在一定的函數關系，損傷程度也會因損傷位置而變化，以上因素促進了損傷程度的判定。

2.1 MSAA 系數分析

一般連續梁橋損傷程度相同、位置不同的MSAA 系數差別較大；當位置相同時，MSAA 系數會隨損傷程度增大而增大。為驗證以上描述，做圖2 和圖3 予以進一步分析，其中損傷程度為30%的不同位置的MSAA 系數如圖2 所示，20m損傷位置處不同損傷程度的MSAA 系數如圖3 所示。分析圖2 和圖3 可知，MSAA 系數峰值能量較集中，變化較規律且相同損傷位置損傷程度與MSAA 系數呈現一定冪函數關系。

圖2 不同橋面位置MSAA 系數

圖3 不同損傷程度MSAA 系數

2.2 損傷程度指標

已知MSAA 系數與車體加速度響應差密切相關，而車速度響應差突變則與橋梁撓度相關，因此MSAA 系數與撓度間存在關系且相同位置MSAA 系數會隨損傷程度而變化，不同位置的MSAA 系數存在明顯差異，因此考慮撓度差、MSAA系數和位置等方面構建損傷程度指標。

由公式（1）、公式（2）可以獲得橋梁的撓度差值f2（x）-f1（x），將損傷位置處的MSAA 系數與相同位置的橋梁撓度差相除，可得到相同位置的橋梁損傷指標系數E1，如公式（6）所示。

式中：mw為同一損傷位置處的MASS 系數；xθl為某跨損傷位置距其左端的距離。

由于橋梁邊跨支座為鉸鏈，中跨相當于固定支座，因此橋梁中跨和邊跨之間的損傷程度存在一定差異且橋梁跨徑對橋梁損傷也有影響，需要通過調整系數E2予以區分，如公式（7）所示。

式中：xθl為損傷位置距某跨左端的距離；xθr為損傷位置距某跨右端的距離；lb為橋梁跨徑長度；k2=1.4+0.3×（n-1），其中n為橋梁跨徑數量。

基于以上分析，結合撓度差、MASS 系數和損傷所處位置等很多因素，構建不同跨徑連續梁橋的損傷程度指標E，如公式（8）所示。

2.3 橋梁損傷程度判定函數

基于上述分析，橋梁損傷程度與損傷指標之間存在一定函數關系。為使相同損傷程度的不同損傷位置的損傷指標值更有辨識度，對其進行歸一化處理，使其保持在一定合理范圍內。基于公式（8）可獲取損傷程度指標值，利用Python相應函數進行擬合，獲取損傷程度與損傷程度指標間的函數關系S（x），將其作為知識庫，可以適用于不同跨徑的連續梁橋。然后將損傷程度指標帶入擬合好的損傷程度函數，可確定各位置損傷程度。將20m 損傷位置處不同損傷程度指標數值進行擬合，如圖4 所示。擬合后的S（x）表達式如公式（9）所示。

圖4 20m 損傷位置處損傷程度函數S（x）擬合圖

3 試驗分析

3.1 基于響應差損傷判定結果分析

橋梁損傷識別研究一般通過引入裂縫單元或者剛度折減來進行模擬。為更好體現基于響應差的損傷判定模型的有效性，該文利用剛度折減來模擬橋梁損傷。為進一步驗證橋梁損傷程度判定方法的有效性，構建相同跨徑的8 種不同橋梁損傷情況，具體見表1。利用公式（8）擬合得到損傷程度函數，將損傷程度指標帶入損傷程度函數實現對橋梁損傷程度的判定，將損傷函數得到的損傷程度指標與實際損傷程度進行對比，見表1。

表1 橋梁損傷情況劃分及判定表

根據表1 可知，該方法的最大判定誤差為4.85%，精度在允許范圍內，并在一定程度上緩解了狀態數據不全帶來的問題，表明該方法可以確定橋梁各種情況下的損傷位置和損傷程度，能滿足對橋梁損傷判定的實際需求。

3.2 不同跨徑橋梁判定結果分析

橋梁跨徑對橋梁損傷狀態的判定具有重要意義，為驗證該方法對不同跨徑組合橋梁損傷判定的準確性，構建了2 種跨徑組合橋梁，利用公式（8）擬合損傷程度函數，將損傷程度指標帶入損傷程度函數實現對橋梁損傷程度的判定，見表2。

表2 不同跨徑組合橋梁損傷情況劃分及判定表

由表2 可知，不同跨徑組合的情況下，基于響應差的橋梁損傷判定方法均能實現橋梁損傷的有效判別，其中最大判別誤差僅為3.80%，能夠滿足實際的精度需求。

3.3 不同剛度組合橋梁判定結果分析

橋梁剛度是進行撓度計算的重要參數，為驗證該方法對不同剛度組合橋梁損傷判定的準確性，通過構建不同跨徑并組合，改變橋梁剛度，利用公式（8）擬合損傷程度函數，將損傷程度指標帶入損傷程度函數實現對橋梁損傷程度的判定，見表3。

表3 不同剛度橋梁損傷情況劃分及判定表

由表3 可知，最大判定誤差為4.17%，判定精度在允許范圍內，表明基于響應差的判定方法能夠適應不同剛度的橋梁，能夠滿足工程實際需求。

4 結論

該文針對老舊橋梁狀態數據缺乏，提出基于響應差的連續梁橋損傷程度識別方法。通過改變牽引車配重，檢測出車輛先后通過橋體時的加速度響應差，對其進行離散小波變換，利用撓度差、MSAA 系數和不同位置構建損傷程度指標，并對大量損傷程度指標的擬合得到適用于不同情景的損傷程度函數知識庫，進而實現對損傷位置的精準識別。最后對相同跨徑不同損傷情況、不同跨徑組合和不同剛度的橋梁損傷情況進行損傷程度判定，判定結果精度均在允許范圍內，表明了該方法的有效性。