基于RBF神經網絡自適應滑模的機器魚運動控制

王治平,李宗剛,陳引娟,杜亞江

(1.蘭州交通大學機 電工程學院,蘭州 730070;2.蘭州交通大學 機器人研究所,蘭州 730070)

0 引言

為了更好的開發利用水下資源以及對水下生物的生活習性進行觀察研究,越來越多的自主水下機器人(AUV)被成功研發。相比于傳統螺旋槳驅動的水下航行器,仿生機器魚作為一種新型水下機器人,在水中作業時具有游動效率高、機動性能好、運動阻力小、隱身性能優良等優點[1-7]。由于水下工作環境的復雜性和任務的特殊性,仿生機器魚在水下作業時往往需要靈活多變的三維運動以規避障礙物并完成預設任務。

近年來,對于仿生機器魚的運動軌跡控制已經取得了一定的研究成果。Saurab Verma等[8]研發了無胸鰭,單自由度尾鰭的機器魚樣機,通過魯棒自適應方法實現了機器魚的轉彎運動控制。Su等[9]在裝有陀螺儀的三關節機器魚上通過PID控制方法對機器魚的轉角進行控制。Li等[10]使用自適應學習算法對雙連桿機器魚的速度和轉彎運動進行控制。Wu等[11]在具有四關節身體2自由度胸鰭以及可轉動頭部的機器魚樣機上,通過更改中央模式發生器(CPG)的參數,實現了機器魚的直游、轉彎、上浮下潛等運動模態。李宗剛等[12]團隊設計了2自由度胸鰭與單關節尾鰭的仿生機器魚,并對機器魚的轉彎特性進行了分析,通過實體實驗驗證了其理論的可行性。Wang等[13]利用線性二次調節(LQR)方法控制具有沉浮機構的機器魚,實現了上浮下潛等水下三維運動。Wang等[14]控制具有單關節尾鰭與搖翼運動的機器魚,實現了空間螺旋運動。相比于陸地環境,仿生機器魚作業的水下環境中存在著復雜的流體運動等非線性擾動,難以建立精確的機器魚水動力學模型。目前仿生機器魚的運動控制大多停留在平面運動或俯仰運動范圍[10,15-18],對于閉環三維運動控制問題尚未完全解決。同時研究者所開發的機器魚樣機大多是以單自由度或2自由度擺動的胸鰭,難以對真實魚類的胸鰭運動進行模擬,降低了機器魚運動的靈活性和機動性,限制了機器魚的最小轉彎半徑等運動特征。

本文通過RBF神經網絡與滑模控制算法相結合的方式控制機器魚運動,并使其運動軌跡快速收斂至設定期望值。RBF神經網絡具有學習規則簡單,收斂速度快,泛化能力強的特點,且對任意非線性系統能進行有效逼近[19-22],所以采用RBF神經網絡算法根據系統的誤差信號對機器魚動力學模型進行實時在線逼近修正。滑模控制算法具有簡單、魯棒性能好,可靠性高的特點,廣泛應用于水下機器人控制[23-24]。為降低滑模控制所帶來的抖振問題,本文采用飽和函數的方法實現控制器輸出信號的連續切換,通過李雅普諾夫定理證明了機器魚運動控制系統具有漸近穩定性,提高了機器魚運動控制魯棒性的同時拓寬了其作業場景。

針對以上問題,本文設計制作了具有3自由度胸鰭以及三關節尾鰭的仿生機器魚樣機。通過分析其運動機理構建了機器魚的水動力學模型,并采用RBF神經網絡控制與滑模控制相結合的算法。通過系統的仿真數學模型,對機器魚三維空間運動軌跡的跟蹤效果進行了仿真驗證,同時使用仿生機器魚樣機進行螺旋下潛運動的實體實驗,進一步驗證了本文所述方法的有效性。

1 仿生機器魚動力學模型

1.1 推進機構運動學建模

通過對魚類胸鰭運動的觀察分析[25],設定剛性3自由度胸鰭高效擺動規律方程為

θ1=-A1cos(2πf1t+φ)+θ1a

θ2=-A2cos(2πf2t)+θ2a

θ3=-A3cos(2πf3t)+θ3a

(1)

式中:fi(i=1,2,3)為頻率;φ為前后與上下拍翼的相位差;θ1、A1、θ1a為前后拍翼的角位移、幅值、偏置;θ2、A2、θ2a為上下拍翼的角位移、幅值、偏置;θ3、A3、θ3a為搖翼的角位移、幅值、偏置。

根據螺旋運動規律可知,取式(1)中A1=π/4,A2=π/8,A3=π/2,θ1a=θ2a=θ3a=0,得胸鰭擺動軌跡曲線如圖1所示,仿生機器魚在此運動規律下,可產生前進運動和俯仰運動的推力分量。

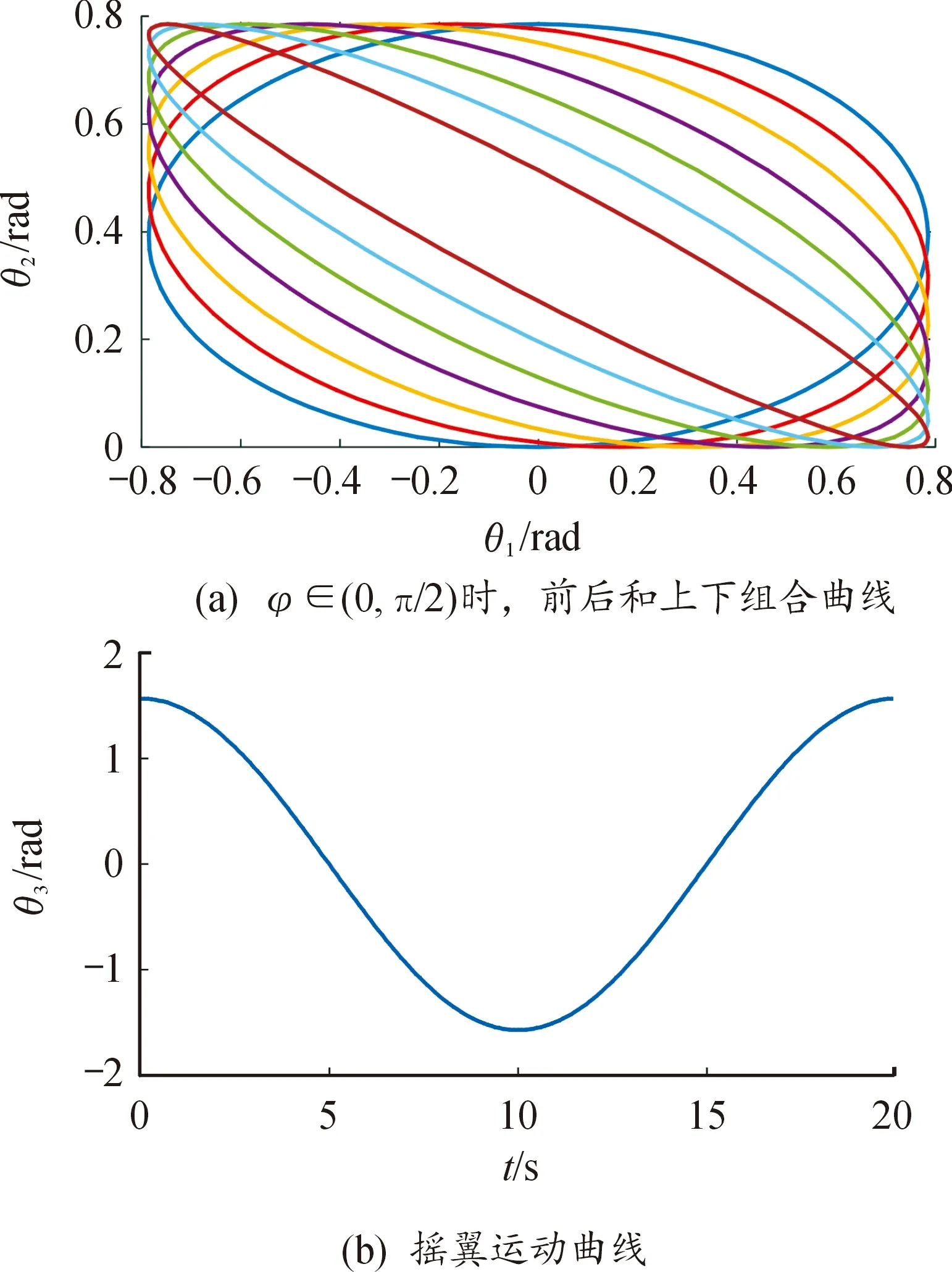
圖1 胸鰭擺動軌跡曲線Fig.1 Pectoral fin swing trajectory curve

1.2 推進機構動力學分析

仿生機器魚在水中受力為胸鰭后擺推進力、回程阻力、形體阻力以及附加質量力等。推進力主要由胸鰭擺動和尾鰭擺動產生,其中利用3自由度胸鰭擺動可以實現機器魚水平面的前進與垂直面的俯仰運動,利用尾鰭擺動時的偏置可實現機器魚的轉彎運動。

1) 胸鰭推進動力學分析。根據胸鰭運動學模型,通過理論力學中“微元積分法”對胸鰭進行受力分析[26],可得胸鰭推進方程為

(2)

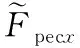
2) 尾鰭推進動力學分析。根據三關節尾鰭擺動規律,對x方向推進力分析[27]可得:

Ftail=2πρS(fh0)2sin(2πft)cos[α0cos(2πft-γ)]

{2πsin(2πft)-tan[α0cos(2πft-γ)]/St′}

(3)

3) 胸/尾鰭協同推進動力學分析。當φ∈(0,π/2)時,胸鰭擺動可產生x和z軸正方向推力分量,調節φ的取值,使其在垂直方向實現俯仰運動。其胸鰭推進力為

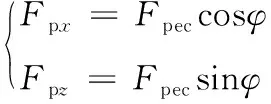
(4)

當尾鰭以偏置β擺動時,將為機器魚運動提供y方向的側向力,實現其轉彎運動行為。此時機器魚尾鰭推力為

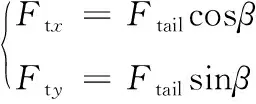
(5)

綜合式(2)—式(5),仿生機器魚螺旋運動動力學方程為

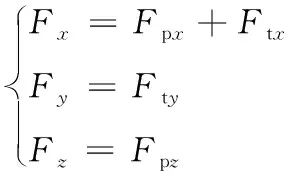
(6)

其中,Fx,Fy,Fz分別是機器魚x,y,z方向所受的合外力。

1.3 仿生機器魚動力學建模

仿生機器魚在水中運動時,受到各個方向的力和力矩,建立動力學模型[28]如下:

(7)

式(7)中:

M=MRB+MA

C(υ)=CRB(υ)+CA(υ)

D(υ)=D(υ)+Dn(υ)

其中:η=[x,y,z,φ,θ,ψ]T表示機器魚運動位姿,υ=[u,v,w,p,q,r]T表示機器魚運動速度,J(η)表示轉換矩陣,形式見文獻[28];MRB表示剛體質量及慣量矩陣;MA為附加質量矩陣;CA(υ)為附加質量引起的類科里奧利/向心力矩陣;CRB(υ)為機器魚質量引起的科里奧利/向心力矩陣;D為線性阻尼矩陣;Dn(υ)為非線性阻尼矩陣;g(η)是機器魚位置和姿態有關的恢復力(力矩);τ為機器魚受到的推力(力矩),由式(6)可得;τE包含機器魚受到由風、浪和流等環境干擾力引起的力(力矩)。

2 仿生機器魚控制器設計

本文在所構建的機器魚水動力學模型基礎上,采用RBF神經網絡控制器對機器魚動力學模型的不確定項和水流干擾項在線逼近,并采用滑模控制其趨近速度和精度。RBF神經網絡自適應滑模控制器架構如圖2所示。

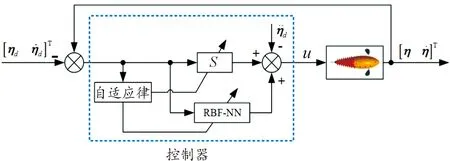
圖2 RBF神經網絡自適應滑模控制器架構Fig.2 RBF neural network adaptive sliding mode controller architecture

2.1 控制律設計

(8)

式中,e1、e2分別為運動軌跡誤差、軌跡誤差變化率。

根據式(7)和式(8),可建立如下所示描述狀態空間的非線性不確定系統:

(9)

式(9)中:

d(e,v)=-J(e1)M-1τd

u=J(e1)M-1τ

2.1.1神經網絡逼近模型不確定項和環境干擾

由于機器魚實際運動中,式(9)中的不確定項為模型的不確定項f(e,v)和水流及環境干擾d(e,v)。因此,本文通過神經網絡算法對不確定項進行在線逼近,從而減少動力學模型的誤差。將不確定項定義為

F(e,v)=f(e,v)+d(e,v)

(10)

由RBF神經網絡算法原理,可知

F(e,v)=W*Th(e)+ε

(11)

式中,h(e)=exp(-(e-m)2/σ2),h(e)為隱含層輸出,e為隱含層輸入;W*為最優權值。

在機器魚實際運動中,根據式(10)和式(11)得未知項逼近:

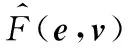
2.1.2滑模控制面設計

設計滑模面

S=e2+Ce1

(13)

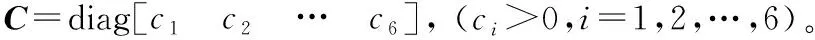
則

(14)

將本文的非線性系統(式(9))代入式(14)可得:

(15)

為了減少速度輸出存在抖動,本文使用飽和函數sat(S),因此選擇的趨近律為

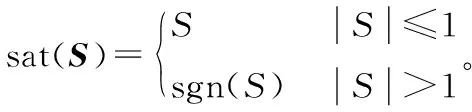
2.1.3滑模控制律和自適應控制律設計

(16)

(17)

(18)

其中,λ和γ均為正常數。

2.2 穩定性證明

(19)

對于自適應滑模控制律和自適應律,本文使用Lyapunov函數分析控制器的穩定性。

定義Lyapunov函數為

V(t)=V1(t)+V2(t)+V3(t)

(20)

對式(20)求導可得

(21)

其中

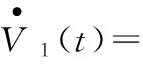
故而

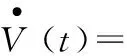
(22)

將自適應律式(17)和式(18),代入式(22)得

(23)

3 仿生機器魚螺旋運動模態分析

在螺旋運動的仿真實驗中,設定機器魚的期望軌跡為空間螺旋線,其運動方程為

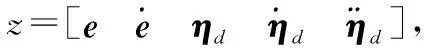
稱取八角楓藥材適量，烘干、磨粉，加水1 000 mL煎煮3 h，濾過；再加水600 mL煎煮2 h，濾過；合并兩次濾液，濃縮，得質量濃度為1 g/mL（按生藥量計）的八角楓水提液。

通過Matlab/Simulink運行仿真程序,得到機器魚x,y,z方向位置和姿態角位移曲線如圖3所示,可知機器魚在運動初始階段與期望軌跡有偏差,在1 s以后其運動軌跡和期望軌跡基本重合,軌跡跟蹤效果顯著。

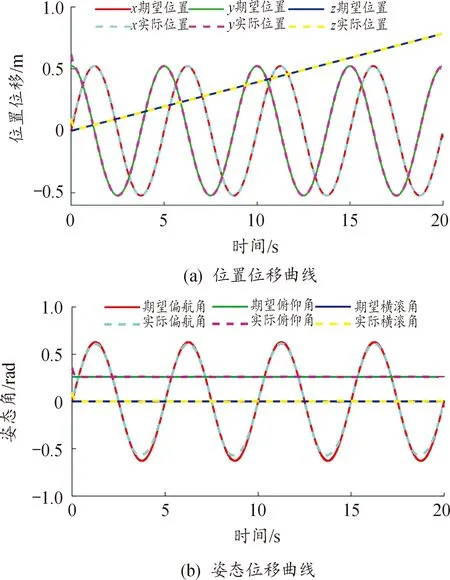
圖3 機器魚位置和姿態位移曲線Fig.3 Robotic fish position and attitude displacement curves

通過將x、y、z三個方向的位移曲線進行空間疊加,可得到機器魚螺旋運動空間位移曲線如圖4所示。

圖4 機器魚螺旋運動空間位移曲線Fig.4 The spatial displacement curve of the spiral motion of the robotic fish

由圖4可得,機器魚的實際運動軌跡和期望運動軌跡基本吻合,僅在運動初始階段存在一定的位置誤差。該現象發生的原因主要在于螺旋運動開始時機器魚的位姿和期望位姿差異較大,執行器的快速動作破壞了原有穩定的水下環境,隨后在控制器的作用下該位置誤差得到了快速收斂。同時得到機器魚各軸向速度及角速度的實時跟蹤曲線如圖5所示。

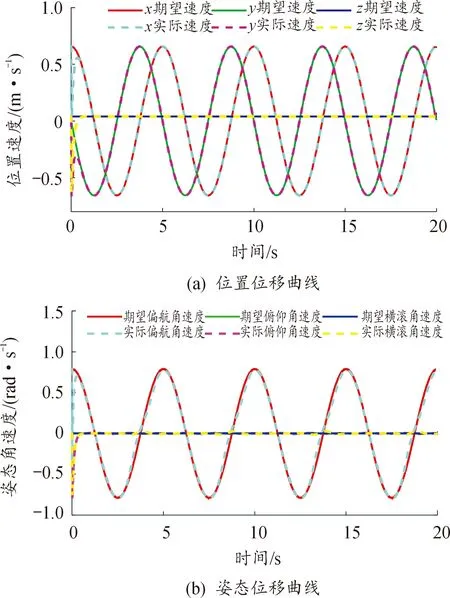
圖5 機器魚螺旋運動速度跟蹤曲線Fig.5 Robotic fish spiral movement speed tracking curve

圖5中(a)為x、y、z三個方向的線速度曲線,圖5(b)分別為繞x、y、z三個軸的角速度曲線。由圖可知,機器魚的線速度和角速度在螺旋運動開始約0.5 s以后與期望值相吻合。同時速度和角速度曲線過渡平滑無尖點,運動開始時速度的跳躍突變也印證了位置誤差出現的原因。

圖6展示了機器魚運動過程中實際位置和期望位置的誤差曲線。

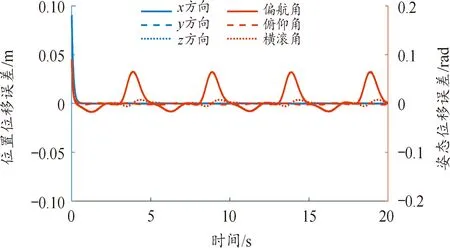
圖6 機器魚螺旋運動位姿誤差曲線Fig.6 The spiral motion position error curve of robotic fish

由圖6可知,機器魚的軌跡誤差始終保持在較小的范圍內,說明控制效果良好。圖7為系統控制輸入,位置和姿態輸入信號均平滑穩定且抖振較小。

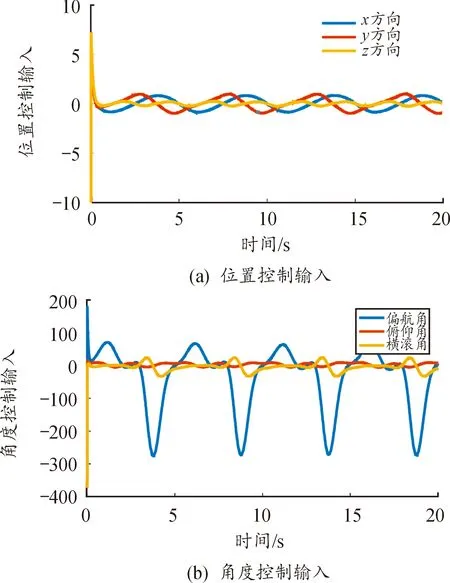
圖7 系統輸入控制信號Fig.7 System output control signal

通過對上述仿真結果的分析可知,本文所設計控制算法可以有效實現機器魚的空間運動控制,同時也驗證了該算法具有較快的收斂速度以及較好的穩定性,機器魚空間運動軌跡平滑無較大波動,也證實了采用飽和函數代替符號函數的方法可有效降低滑模控制所產生的抖振現象。

4 實驗驗證

4.1 實驗平臺和環境

1) 實驗平臺。本文使用自主研發設計的3自由度胸鰭和三關節尾鰭協同推進的仿生機器魚,其形狀近似于流線型橢球,長×寬×高為0.65 m×0.17 m×0.23 m,總質量約為9 kg;內部裝有深度傳感器和陀螺儀,可實時監測運動位姿,如圖8所示。

圖8 仿生機器魚實驗樣機Fig.8 Experimental prototype of biomimetic robotic fish

2) 實驗環境。本文仿生機器魚的實驗水池長、寬和高分別為4.0 m、2.0 m和1.2 m,主要模擬靜水環境,用于圖像采集的攝像頭距水池上方約3 m,池內水深約1 m。水池實驗環境如圖9所示。

圖9 仿生機器魚水池環境Fig.9 Biomimetic robot fish pool environment

4.2 螺旋下潛實驗

采用所研制的仿生機器魚樣機,分別在實驗室水池進行靜水和動水2種工況下的實驗。

1) 水池靜水實驗。在螺旋運動實體實驗時,控制機器魚胸鰭按式(1)規律運動,通過讀取深度傳感器和陀螺儀模塊的反饋數據,使得控制器實時輸出控制機器魚胸/尾鰭運動的參數。靜水工況機器魚螺旋下潛運動如圖10所示。

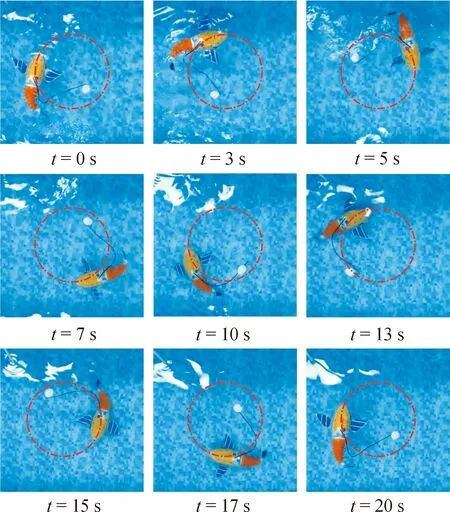
圖10 靜水工況機器魚螺旋下潛運動Fig.10 Spiral diving motion of robotic fish under still water conditions

圖11顯示水池實驗中機器魚空間運動軌跡。通過對比發現機器魚在螺旋下潛的初始階段存在較大位置誤差,約8 s后實際運動軌跡能更好的跟蹤期望軌跡。當機器魚運動至接近水池邊緣和離開水池邊緣區域時運動軌跡略有變形,導致該現象的主要原因是當機器魚處于水池邊緣時壁面效應加劇產生了較大的擾動。如圖12所示,機器魚在運動初始階段有較大的位置誤差,最大達0.1 m;8 s后位置誤差顯著降低,最大為0.06 m。機器魚整體運動軌跡誤差較小且無明顯尖點,雖略有滯后但可保持平穩螺旋運動。

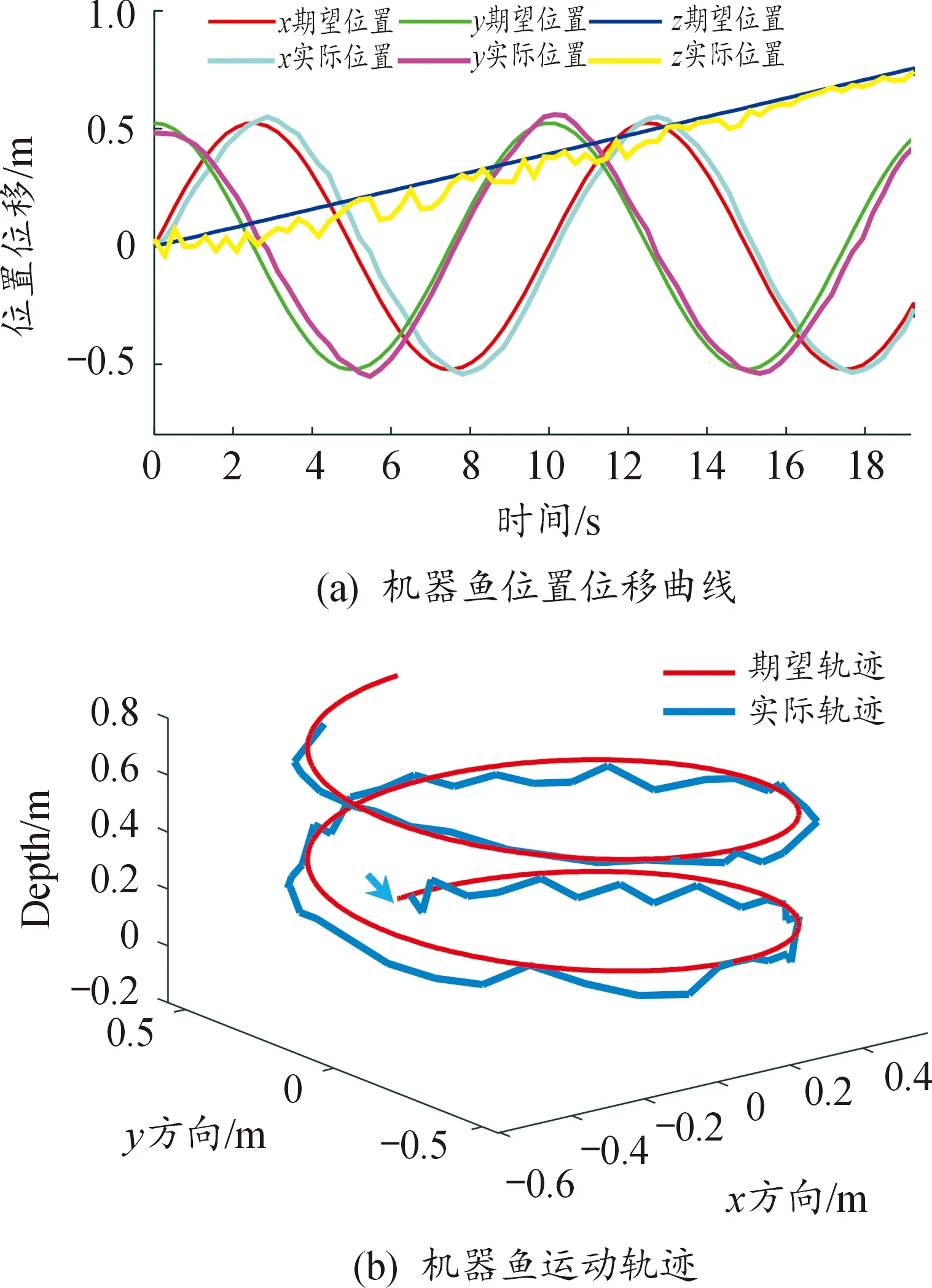
圖11 機器魚空間運動曲線Fig.11 Three-dimensional motion curve of robotic fish

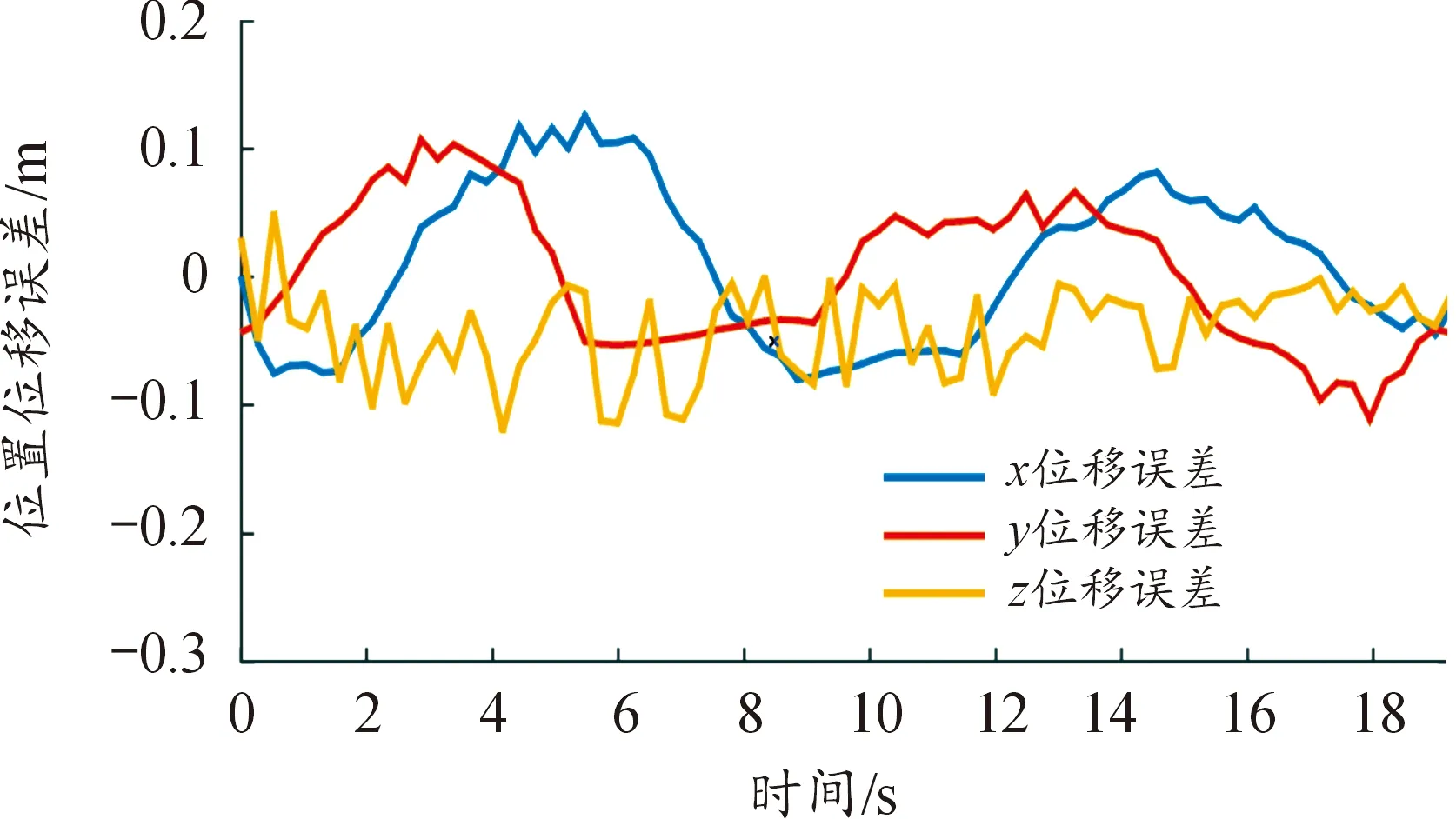
圖12 機器魚實際軌跡誤差曲線Fig.12 Actual trajectory error curve of robotic fish

2) 水池動水實驗。利用變頻潛水泵搭建不同流速下的循環水池工況,其水流方向如圖13黃色箭頭方向,流速設定為0.1、0.3、0.5 m/s。對仿生機器魚設定不同流速情況下與靜水工況實驗一致的運動規律,并采集其運動位姿數據。動水工況機器魚螺旋下潛運動如圖13所示。

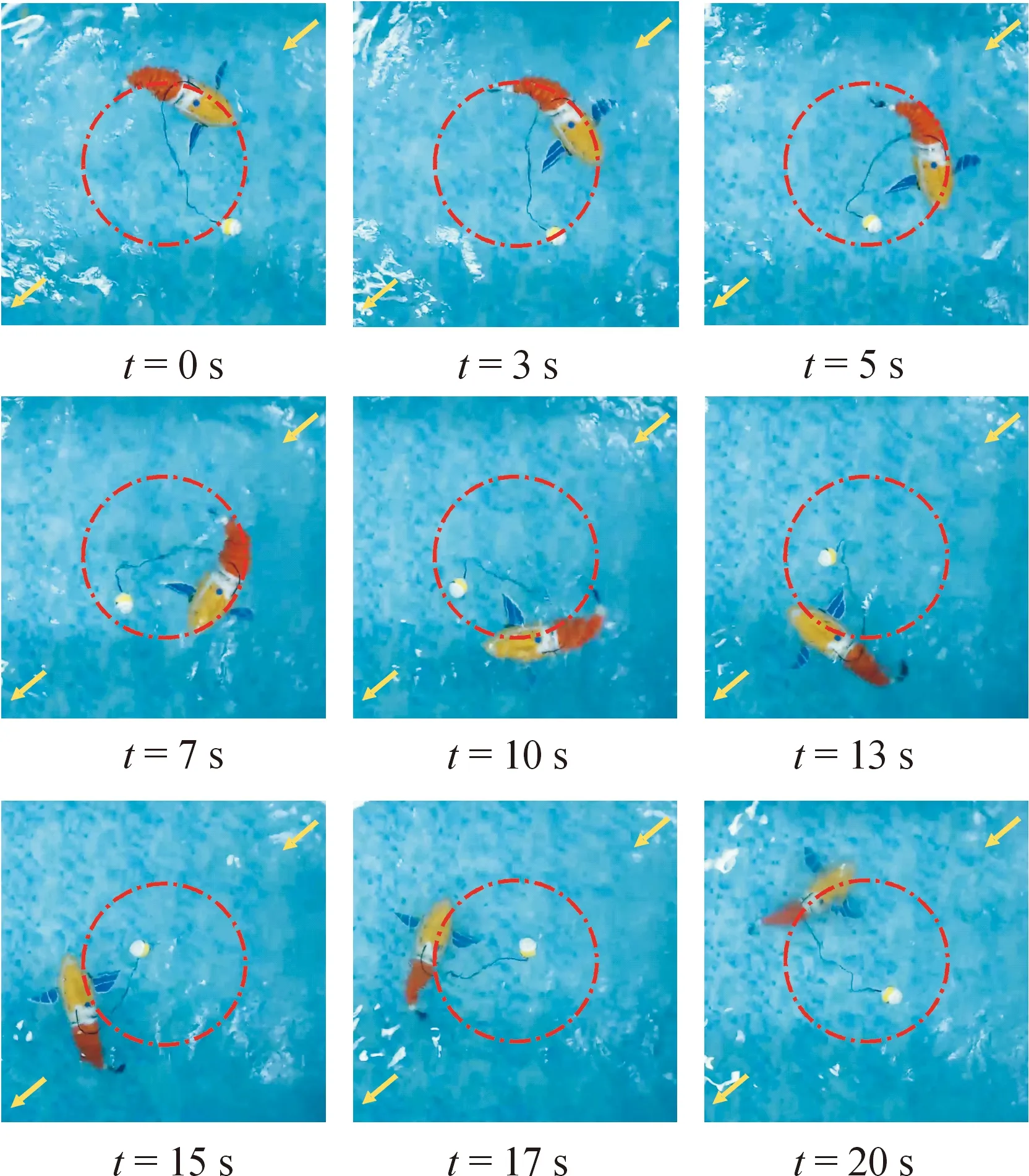
圖13 動水工況機器魚螺旋下潛運動Fig.13 Spiral diving motion of robotic fish under dynamic water conditions

如圖14所示,在0.1 m/s流速下機器魚運動位置誤差和靜水工況基本一致,而在0.3 m/s和0.5 m/s流速下,機器魚運動朝水流方向有明顯的滑移,流速越大滑移越大,最大達0.08 m,8 s后由于其潛入水中,滑移顯著降低。但機器魚運動誤差較靜水工況無明顯變化,在3～7 s和13～17 s階段,由于水池的壁面效應,其軌跡在靠近壁面處略有變形,誤差較大,且流速越大壁面效應影響越大,將會出現流速與滑移不對應的情況,具體見圖14中局部放大圖所示。

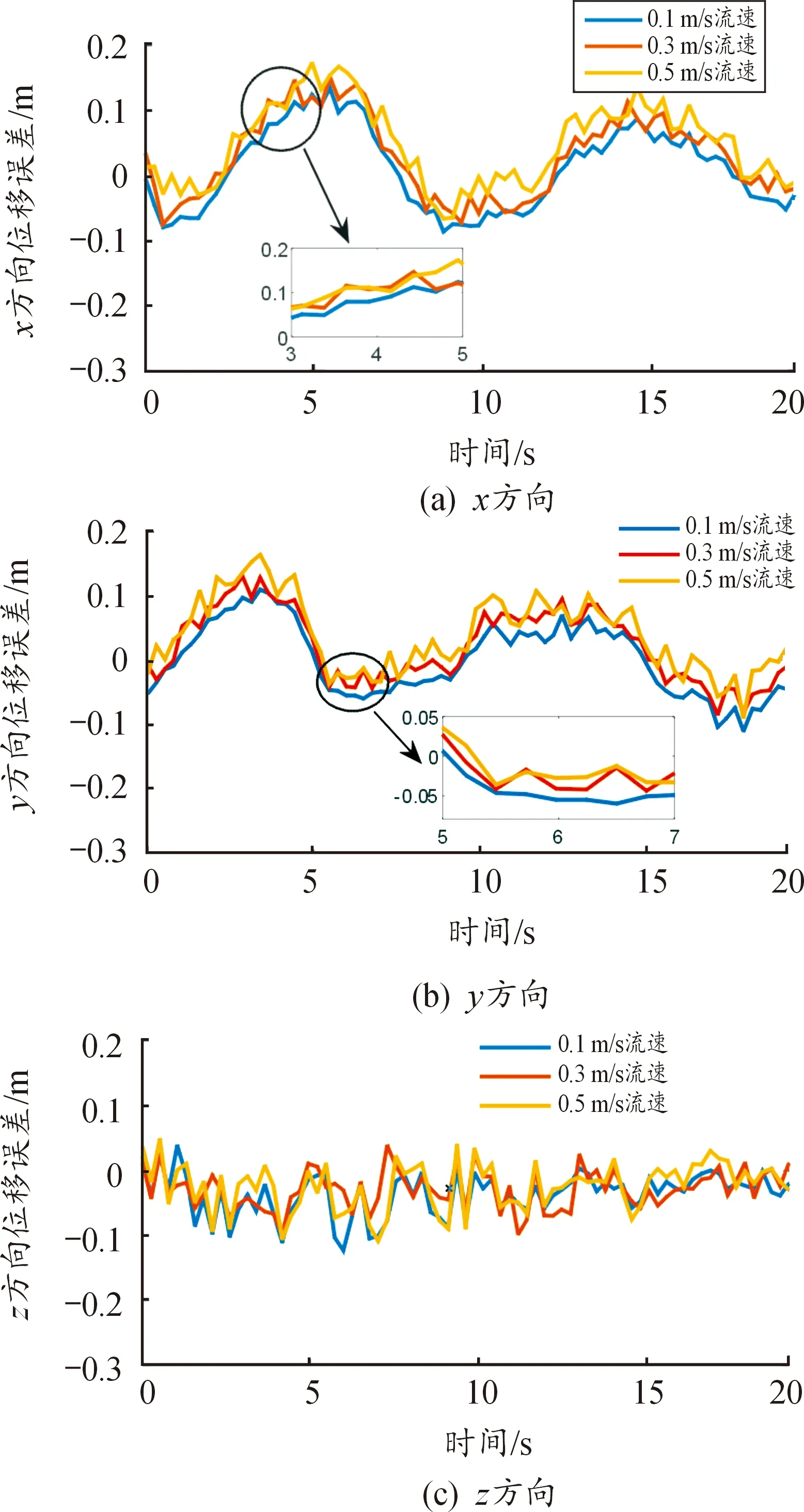
圖14 不同流速下機器魚實際軌跡誤差曲線Fig.14 Actual trajectory error curve of robotic fish with different flow rates

通過水池動靜水實體實驗表明,水流對機器魚螺旋運動時滑移影響較大,但運動軌跡依舊保持螺旋運動,并與期望基本保持一致,進一步驗證了本文所設計控制方法的有效性,同時說明了所構建的仿真模型具有可參考性。

5 結論

本文針對3自由度胸鰭仿生機器魚空間軌跡跟蹤控制問題,在所建立胸鰭運動軌跡方程和水動力學模型基礎上,提出了一種基于RBF神經網絡自適應滑模控制方法。

1) 設計制作了具有3自由度胸鰭以及三關節尾鰭的仿生機器魚樣機,通過分析機器魚運動機理設定胸鰭運動軌跡曲線并構建了機器魚水動力學模型。

2) 通過RBF神經網絡實現對機器魚模型的實時逼近和補償,并使用滑模控制方法實現運動軌跡的快速收斂,利用李雅普諾夫穩定性定理證明了該方法具有漸近穩定性。

3) 使用仿生機器魚樣機進行了室內水池實驗,實驗結果表明機器魚在不同流速工況螺旋下潛運動時運動過程平穩,可實時跟蹤空間運動軌跡。由于室內水池的壁面效應,其軌跡在靠近壁面處略有變形,最大軌跡誤差為0.18 m;驗證了本文所述方法的有效性。