基于改進視覺慣性里程計的無人機系統設計

王 瑞,王茂森,戴勁松,管紅根

( 南京理工大學 機械工程學院, 南京 210094)

0 引言

以多旋翼無人機為主的小型空中機器人技術取得了長足發展,廣泛應用于軍事偵察、武裝打擊、人員搜救,場景重建等領域。上述應用場景中,無人機主要依靠工作人員遙控操作,只有少部分可以根據電腦終端設定的軌跡進行小范圍、低復雜度的飛行。小型多旋翼無人機的定位是實現其在復雜環境下自主移動的基本問題,在軍事、民用等多種領域下有著廣闊的應用前景。對于實現無人機的智能化與自主化而言,最重要的前提是無人機能夠利用機載傳感器完成對環境的感知和自身位姿的精確估計。常見機載傳感器有GPS、北斗、慣性測量單元、視覺傳感器和激光傳感器等。GPS、北斗等衛星導航定位系統具有全天候工作、覆蓋范圍廣等特點,將其與慣性測量單元融合,可以獲得較高的位姿估計精度,在軍用和民用無人機上有較多應用,但當無人機在城市或叢林等遮擋嚴重的環境中時,衛星導航系統的定位數據不可靠,甚至無法使用[1]。文獻[2]利用激光雷達產生的點云數據實現無人機在缺乏GPS信號情況下進行自身定位,但激光雷達體積大、且價格昂貴,不適用于小型旋翼無人機。文獻[3]使用單目相機估計無人機位姿并基于Apriltag2進行融合以獲取深度信息,該方法可以彌補單目相機無法獲取環境尺度的缺陷,尺度信息依賴于Apriltag2,在室內場景下有較好效果,但不適用于室外環境。文獻[4]提出了使用RTK技術輔助定位的方案,在室外可以獲得較高的定位精度,但無人機搭載的相機僅用于拍攝與后期數據處理,沒有介紹在RTK信號覆蓋不到場景下的解決方案。文獻[5]則進一步將RTK定位數據融合到基于視覺的定位方案中,通過擴展卡爾曼濾波算法將不同信息進行有效融合,有利于解決由于累積誤差造成的漂移問題,但該方式需要事先在環境中架設RTK基站,不具有普適性。文獻[6]使用視覺與高度傳感器進行無人機在室內環境下的定位,但只適用于低速運動情況,且在室外光線變化大時效果不理想。基于優化的視覺慣性里程計(visual-inertial-odometry,VIO)采用視覺和慣性測量單元緊耦合的方式來估計本體運動狀態[7],充分結合了2種傳感器的特性,在GPS信號缺失的場景下具有定位精度高、成本低等優點,因此該方式逐漸成為當前主流發展趨勢,受到了普遍關注。

針對小型多旋翼無人機在無GNSS信號的復雜場景下對自身位姿的估計問題,在基于優化的視覺慣性里程計基礎上,提出改進的里程計并構建一套無人機系統進行驗證。通過改進后的RANSAC算法剔除外點,設計飛控通信接口與控制模塊并搭建了gazebo仿真環境。實驗驗證,改進后算法具有良好的定位精度與實時性,對無人機在復雜環境下的自主運動具有實際工程意義。

1 視覺慣性里程計

1.1 視覺SLAM數學模型

經典的視覺SLAM數學模型如下:

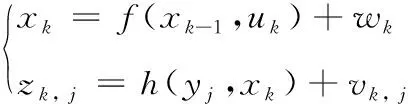
(1)

式(1)表示運動方程和觀測方程,xk與xk-1分別表示k,k-1時刻的位姿,uk表示k時刻的運動輸入量,wk表示對應的噪聲。zk, j表示k時刻,在xk位姿下對yj路標的觀測值,vk, j表示k時刻的觀測噪聲。在視覺慣性里程計中,f(xk-1,uk)由慣性測量單元的數學模型確定,h(yj,xk)由相機投影模型確定。慣性測量單元通過預積分模型構造殘差項,而視覺部分通過重投影誤差構造殘差項,最后利用非線性優化算法求解代價函數即可得到融合后的最優狀態量。

1.2 對極約束與基礎矩陣

相機分別從視角1與視角2觀察三維空間中同一點P,在P點未知的情況下,求解視角1到視角2相機的運動,可以通過對極幾何約束解決,如圖1所示。

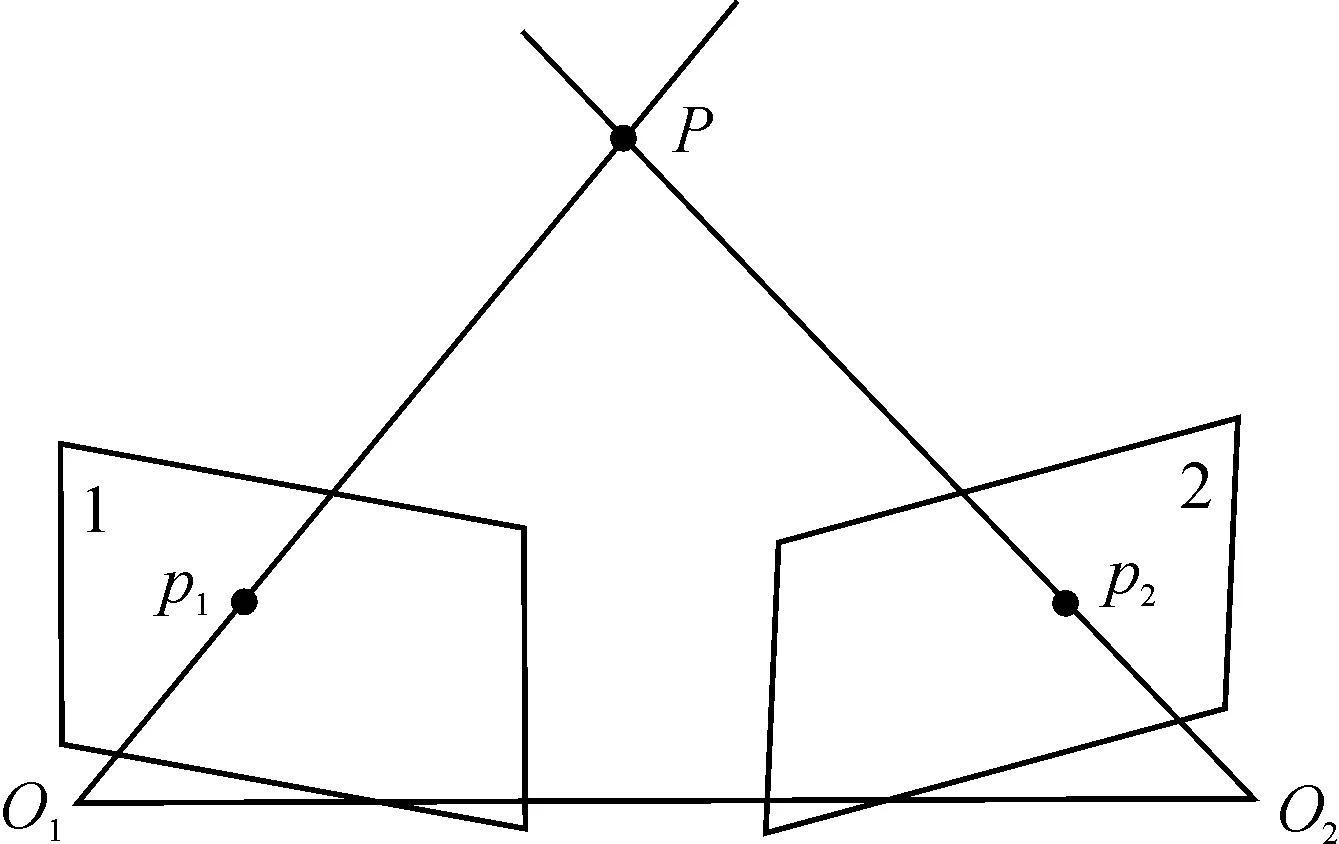
圖1 對極幾何Fig.1 Epipolar geometry

對極約束關系可表示為公式(2):

(2)

式中:p1與p2為真實物理世界中某點P分別在視角1與視角2下的投影,F為3×3的基礎矩陣。p1與p2使用齊次坐標,在相差一個常系數情況下式(2)仍然成立,因此F矩陣的自由度為8,一般使用8點法[8]計算。假設p1=[x1,y1,1]T,p2=[x2,y2,1]T,代入式(2),得到:

(3)

將基礎矩陣F各元素展開為一個向量處理,可得到8點法求解基礎矩陣的一般式。

文獻[9]認為,原始圖像坐標點的齊次值各分量的數量級相差太大,導致8點法求解基礎矩陣的結果不穩定,提出一種預處理方式,先對像素坐標進行歸一化處理,再使用8點法求解基礎矩陣,最后通過基礎矩陣分解得到相機運動的旋轉矩陣和平移向量。

在已知三維空間點和像素點的情況下,可以通過n點透視法(Perspective-n-Point,PnP)求解相機位姿。無論是通過對極約束還是PnP方法求解相機位姿,求解精度與特征點的匹配精度都有很大關系,因此,對前端算法進行改進,通過剔除錯誤匹配點,達到提高里程計精度與魯棒性的目的。

2 改進RANSAC算法剔除外點

2.1 RANSAC算法

根據前端光流追蹤或特征匹配算法,不同視角下兩幅圖像的匹配點通常遠遠大于8對,為充分利用更多的點計算基礎矩陣,可以采用最小二乘算法。但在實踐中考慮匹配存在誤差,由于噪聲的存在,匹配點對之間并不能嚴格遵循式(2),最小二乘算法中錯誤的匹配數據可能會導致結果偏離真實值。隨機采樣一致性算法(random sample consensus,RANSAC)是一種從包含錯誤值的數據中迭代估計模型參數的算法[10]。它具有異常檢測的特性,在視覺慣性里程計中,將錯誤匹配點稱為外點,正確的匹配點稱為內點,借助該算法可以實現2個作用:在缺失3D點時計算基礎矩陣,從而進一步分解出相機的運動姿態;向里程計后端發送匹配點對之前,通過對極約束計算基礎矩陣的方式,盡可能剔除外點,為后端優化創造更好的條件。

傳統的RANSAC算法包含以下幾個步驟:

1) 將所有匹配點集S中的特征點進行歸一化處理。

2) 在匹配點集S中隨機采樣抽取8對點,采用8點法計算基礎矩陣F。

3) 在基礎矩陣F下,計算所有匹配點的重投影誤差e,并與預設閾值T進行比較,當e≤T時,記該點為內點,否則將該點標記為外點,通過內點占總匹配點的比例計算該模型得分score。

4)重復步驟2)、3),直到達到最大迭代次數或滿足內點比例超過預設值,獲取得分最高的結果作為基礎矩陣F,并從匹配點集S中剔除該估計下的所有外點。

2.2 改進的RANSAC算法

2.2.1帶優先級的樣本點采集策略

實際環境中由于存在動態目標的干擾,如果某次采樣的匹配點位于動態目標區域,基礎矩陣的估計可能會失效,盡管RANSAC算法能夠在一定程度上避免這種情況,但傳統RANSAC算法的樣本點采集完全隨機,如果多次采樣都存在樣本點位于動態目標區域的情況,基礎矩陣估計的精度和魯棒性會降低[11]。

因此本文中提出一種帶優先級的樣本點采集策略:首先通過目標檢測算法對潛在的動態目標進行檢測,獲取目標二維包圍框集合B,假設b為檢測結果集合B中某一目標包圍框,其滿足:

b=[cx,cy,h,w]T

(4)

式中:cx、cy表示包圍框b的中心點像素坐標,h和w分別表示包圍框b的高和寬。其次,構造特征容器與哈希表,特征容器的元素保存特征點的二維像素坐標,哈希表的鍵碼k保存特征點在容器中的索引,對應的值記為mp[k],它的值由特征點坐標值與集合B中各包圍框的關系確定,計算公式如下:

(5)

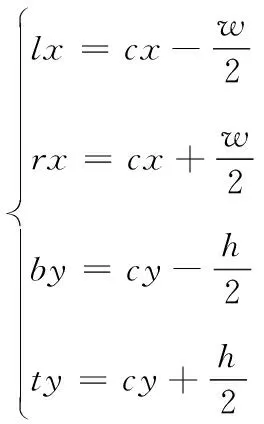
(6)

式(5)中,m為大于0的正整數,px與py表示鍵碼k所對應特征點的像素坐標,改進后帶優先級的樣本點采集策略為:在一次迭代中,對于某特征點p,先在哈希表中查詢其對應值是否為0,如果為0,則將其作為一個樣本點,如果是大于0的正整數,則將其值減1,重新選擇樣本點。通過優先級的設置,在采集樣本點時將優先采集潛在的動態目標區域之外的特征點,從而在一定程度上提高基礎矩陣的估計精度。本文中并沒有將潛在的動態目標包圍框內部的特征點直接剔除,因為僅依靠目標檢測算法獲取的包圍框內的目標并不一定處于運動狀態,如果目標所占圖像比例較大且處于靜止狀態,直接剔除無疑會浪費較多的有效特征點,因此,在不借助其他更加復雜算法如目標跟蹤算法的前提下,通過對預設值m的自減,既提高了包圍框外部特征點優先被采集的概率,又不會完全剔除該部分特征點,一定程度提高了算法的魯棒性。

2.2.2并行化計算

RANSAC算法雖然能夠將匹配點劃分為內點與外點,但如果迭代次數過少,無法保證得到的基礎矩陣精度與外點的剔除效果,迭代次數過多,又會影響系統的實時性。針對該問題的一般做法是先設置一個最大迭代次數,當某次迭代計算得到一個得分最高的F矩陣時,更新迭代次數,如果達到最大迭代次數或當前得分最高的解對應的內點比例超過設定值,則終止算法,具有一定通用性。內點比例的設定是一個經驗值,雖然可以將迭代次數限制在較低水平,在一定程度上保證較高的內點比例,但由于迭代次數的快速下降,最終可能導致所估計的基礎矩陣F不是全局最優解。文獻[12]通過加入預檢驗過程,過濾掉偏差較大的模型參數,一定程度上提高了算法的效率,但計算過程過于復雜。文獻[13]通過對樣本點集合預先設置,使初始樣本集合中內點比例增加,從而減少迭代次數。

針對該問題,采用多線程技術,對基礎矩陣F估計進行并行化計算的改進,達到保證計算效率的同時,提高內點比例的效果。具體地,首先獲取系統當前可用進程數N,開辟n個線程執行改進后的RANSAC算法,其中n≤N。所有線程各自維護一個該線程的最優基礎矩陣。最后,從所有線程中尋找得分最高的基礎矩陣,并將該基礎矩陣對應的所有外點從匹配點集合中剔除。

3 無人機系統軟硬件設計

3.1 硬件系統搭建

系統硬件組成如圖2所示,板載計算機使用Intel NUC11TNKi5,主控芯片為11代酷睿i5系列,具有四核八線程,同時具有8GB DDR4主存。飛控使用Holybro Pixhawk4 mini,其主控為ARM Cortex M7,并內置了BMI055慣性測量元件,輸出頻率可達200 Hz。視覺傳感器使用Intel d455實感相機,分辨率為640×480,幀率設置為30FPS,RGB彩色相機水平視角86°±3°,垂直視角57°±3°。

圖2 系統硬件組成Fig.2 System hardware composition

3.2 軟件總體設計

VINS-Fusion[14]是目前先進的基于優化的多傳感器融合里程計通用框架,將本文改進后的RANSAC算法應用于該系統并作為無人機位姿來源。軟件系統基于ubuntu和ROS框架實現,主要包括部分:改進的視覺慣性里程計、飛控通信接口和控制器,軟件系統工作框圖如圖3所示。

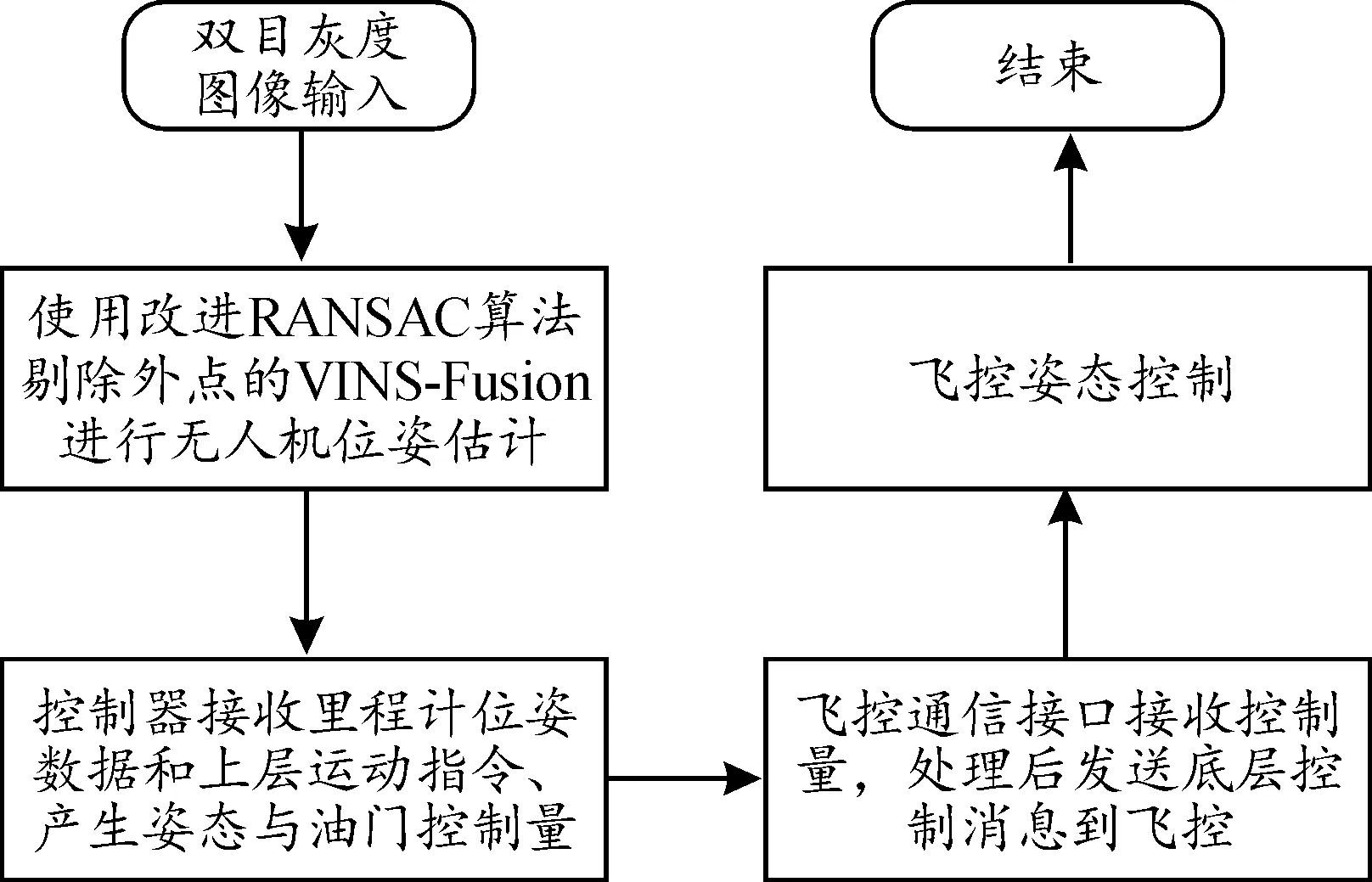
圖3 軟件系統工作框圖Fig.3 Software system block diagram

3.3 飛控通信接口設計

硬件平臺所使用的Holybro Pixhawk4 mini飛控采用mavlink通信協議,在ROS框架下,需要借助mavros功能包與板載計算機進行通信,通過mavros進行飛控狀態查詢、控制量輸出等操作變得異常復雜,為了提高調試與開發的便捷性,設計了專門的通信接口,對mavros話題進行了封裝。

無人機狀態量state包含:連接狀態connected、加解鎖狀態arm、模式mode、系統啟動時間start_time、當前位置pos、當前速度vel、當前姿態q、歐拉角rpy、三軸角速度angular_v和三軸加速度linear_a。其中當前姿態q與歐拉角rpy分別滿足式(7)與式(8):

q=(w,x,y,z)

(7)

(8)

本方案利用不同mavros消息將無人機控制器封裝成接口形式,直接調用相應接口即可實現不同控制方式,控制系統采用狀態模式設計,控制系統狀態轉移圖如圖4所示。

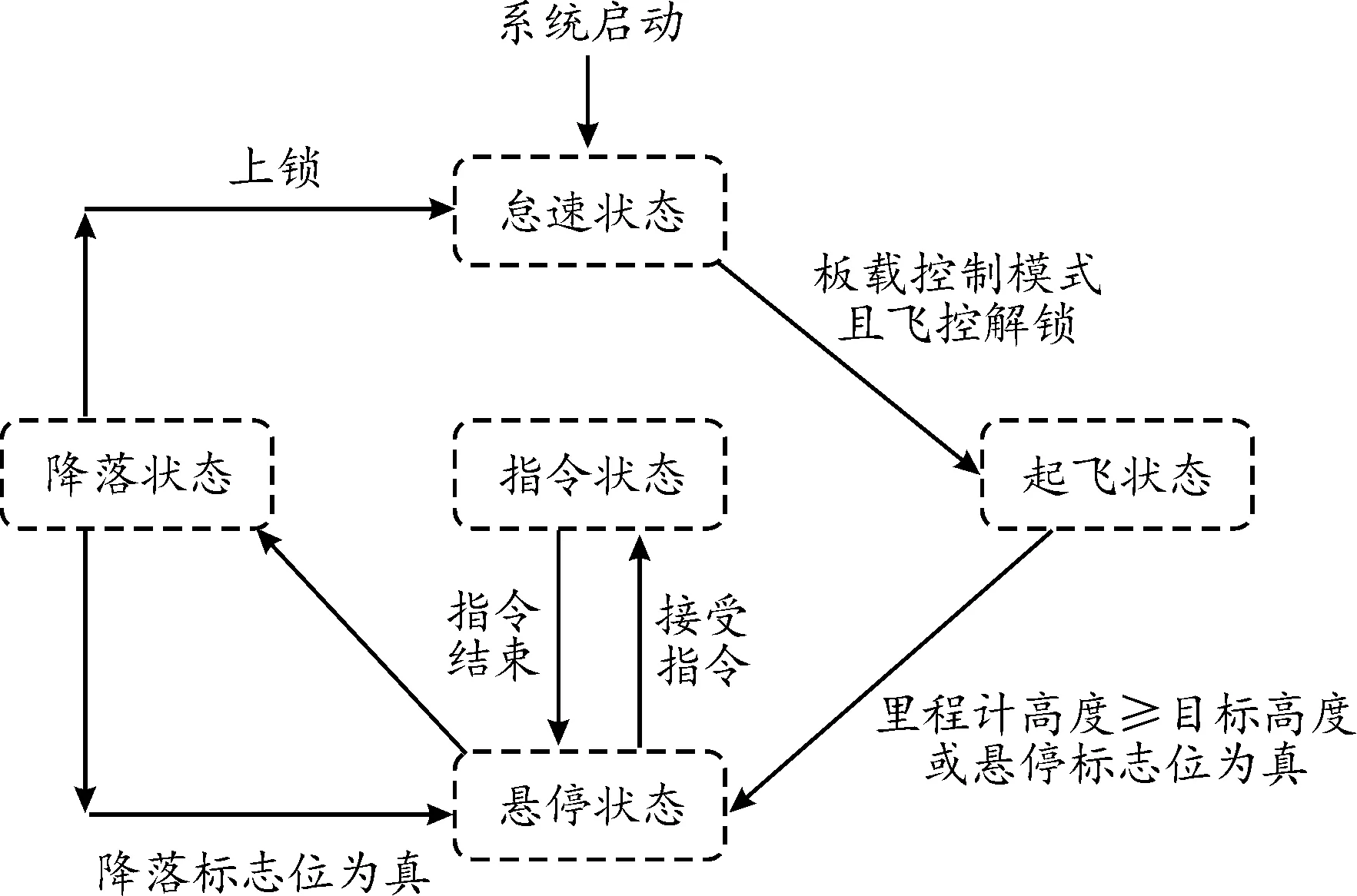
圖4 控制系統狀態轉移圖Fig.4 Control system state transition diagram

3.4 仿真系統

為高效便捷的驗證算法有效性,選取gazebo物理仿真平臺作為本方案的仿真軟件,該平臺能夠提供高保真度的物理模擬。將雙目相機模型搭載于四旋翼無人機,該相機具有90°水平視角,使用開源協議PX4作為飛控軟件,其內部的慣性元件數據及無人機搭載的相機圖像,可作為視覺慣性里程計的輸入數據,仿真框架示意圖如圖5所示。

為模擬現實世界的復雜環境,通過樹木、車輛等模型構建了仿真環境如圖6所示。

4 實驗驗證與結果分析

4.1 改進RANSAC算法實驗

為驗證改進RANSAC算法在實際場景中的效果,本文進行如下實驗,其中所涉及硬件使用圖2所示平臺。如圖7為南京理工大學校園內采集的6組實驗圖像,其中每組圖片由兩幅相機在不同視角下對同一場景拍攝的圖像組成。實驗時直接使用無人機搭載的d455相機拍攝,每幅圖像的分辨率為640×480。特征點使用opencv庫的ORB[15]提取器進行提取,描述子分別使用256位的BRIEF描述子[16]和512位的BAD描述子[17],6組圖像使用傳統RANSAC與改進后算法進行內點比例的比較,置信度設置為0.99,其他參數均一致,結果如圖8、圖9所示。為驗證改進后算法的時間效率,對6組圖像在256位的BRIEF描述子下2種算法分別進行100次測試,并計算平均值,得到結果如圖10所示。

圖7 實驗圖像Fig.7 Experimental image

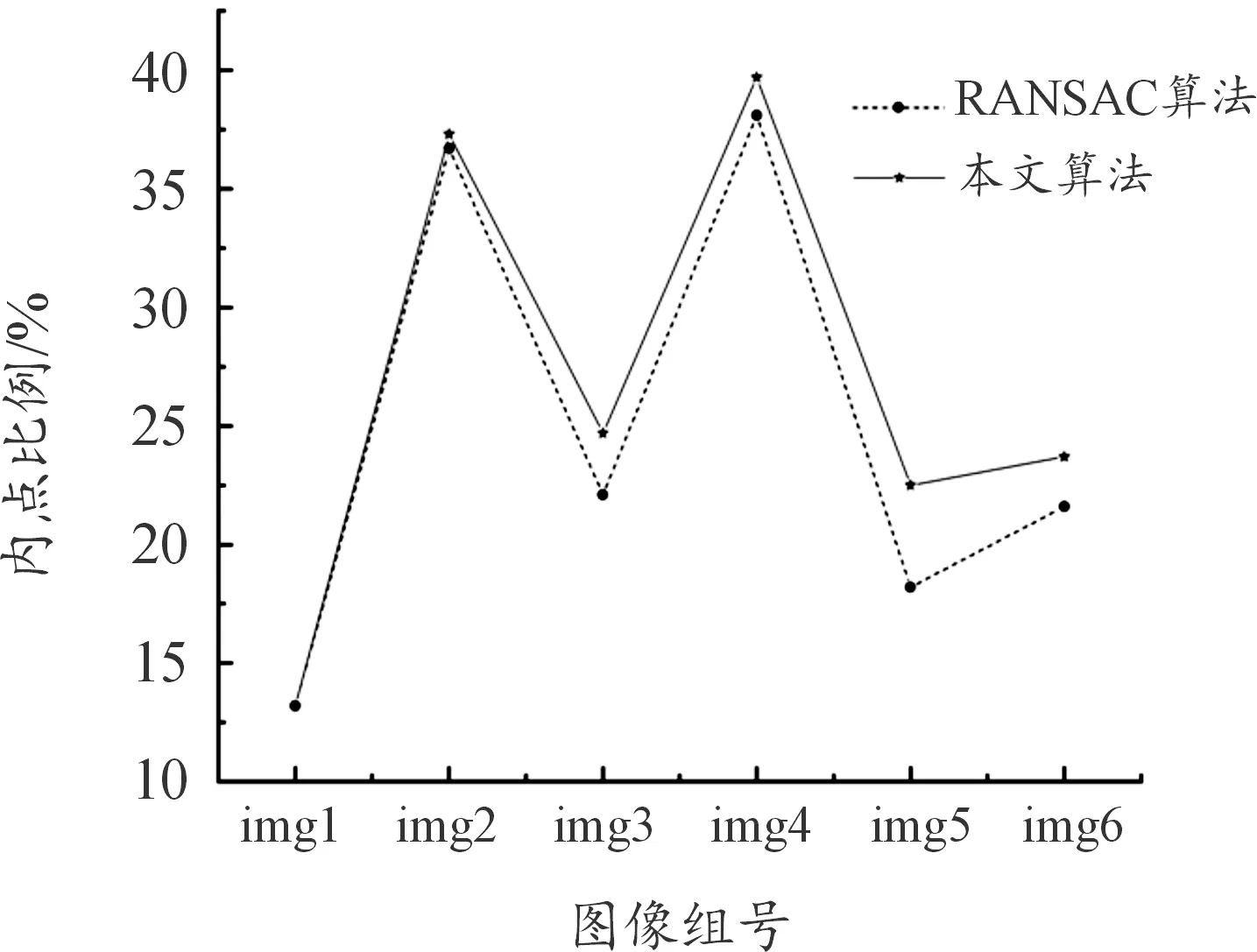
圖8 采用BRIEF描述子的內點比例Fig.8 Inlier scale using the BRIEF descriptor

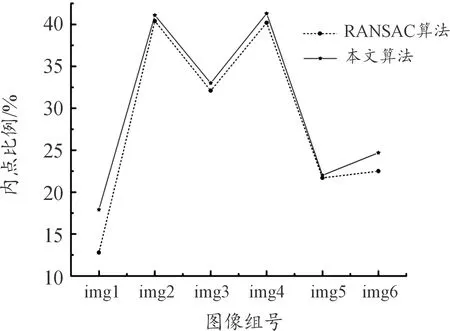
圖9 采用BAD描述子的內點比例Fig.9 Inlier scale using the BAD descriptor

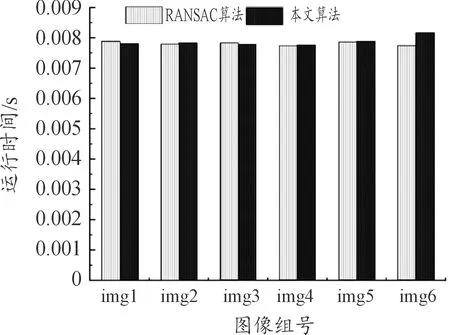
圖10 運行時間對比Fig.10 Running time comparison

分析實驗結果可知,改進的RANSAC算法在運行時間方面與傳統RANSAC算法基本一致,滿足無人機應用中實時性的要求。算法理論上可以獲取更多組解,從而提高基礎矩陣的估計精度,從實驗上看,改進后的算法在不同特征點數目上的內點比例均高于傳統算法,因此能夠更好剔除外點。

4.2 數據集里程計測試

本文使用EuRoC MAV真實場景的視覺慣性數據集[18]評估改進后的算法,數據集使用一個小型無人機采集,其中包括雙目圖像,頻率為200 Hz同步的慣性測量數據,真實狀態使用vicon運動捕捉系統和Leica MS50全站儀提供。在本實驗中,使用MH_01和MH_02兩個數據集評估算法對VINS-Fusion的改進效果,通過evo[19]評估工具對程序運行結果進行分析,軌跡誤差圖如圖11、圖12所示。與未改進的VINS-Fusion在絕對誤差估計下得到的均方根誤差(root-mean-square-error,RMSE)進行對比如表1所示。

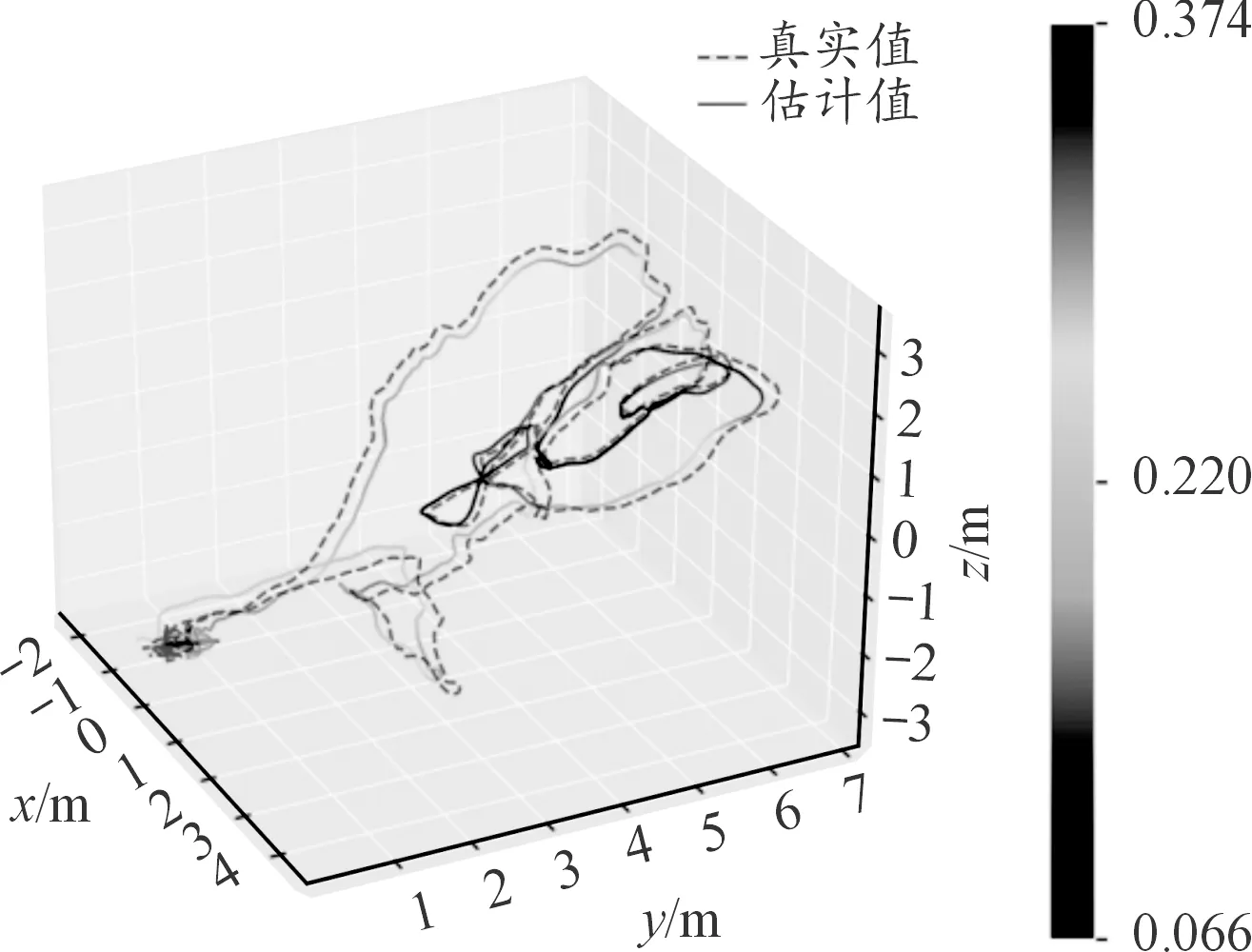
圖11 MH_01軌跡誤差Fig.11 MH_01 trajectory error

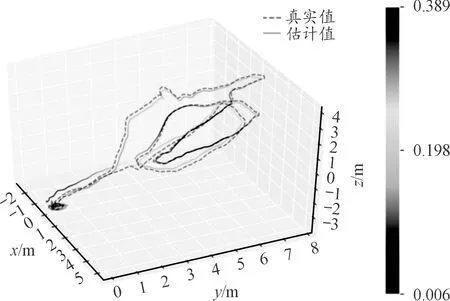
圖12 MH_02軌跡誤差Fig.12 MH_02 trajectory error

表1 RMSE軌跡估計誤差參數Table 1 RMSE trajectory estimation error parameters

最后,使用無人機進行飛行實驗如圖13所示,實驗時Intel d455相機雙目圖像幀率設置為30 FPS,滿足實時性要求。

圖13 飛行試驗Fig.13 Flight experiment

5 結論

1) 改進的RANSAC算法,在計算基礎矩陣時平均內點比例提高1.8%。

2) 將改進的算法嵌入VINS-Fusion,在MH_01序列上的實驗,絕對軌跡誤差的均方根誤差降低了0.001 m,在MH_02序列上的實驗,絕對軌跡誤差的均方根誤差降低了0.019 m。

3) 基于Linux和ROS系統編寫無人機通信接口,簡化了無人機飛控與板載計算機的通信方式,實現上層規劃模塊、控制模塊和底層飛控的解耦。

4) 算法最終部署到所搭建的無人機平臺,達到了30 FPS的實時效果,滿足無人機對實時性的要求。