小型無人機遙控器信號跳頻參數估計方法

徐亞軍,唐文波,魯合德,司成可

(中國民用航空飛行學院, 四川 廣漢 618307)

0 引言

近年來,無人機濫用和黑飛現象時有發生,導致安全事故層出不窮[1]。雷達[2]、聲學[3]、光電[4]等檢測技術成為了檢測無人機目標的主流手段。但是上述檢測技術均存在其不足,而無線電檢測[5]是利用無人機與遙控器之間的控制信號來檢測無人機目標,具有監測距離遠、受環境影響小等顯著特點。

跳頻擴頻信號是典型的非平穩信號,時頻分析法[6]憑借對非平穩信號的分析擁有強大的處理能力成為了無人機信號檢測的主流方法。在該類方法中,線性時頻分析法運算復雜度低、實時性高,但無法同時獲得高時間、頻率分辨力[7]。非線性時頻分析法具有良好的時頻聚集性,但存在運算量與時頻聚集性無法兼得的問題[8-10],這嚴重影響了參數估計的性能。近年來,許多組合時頻估計參數算法被相繼提出,如文獻[11]將STFT和SPWVD相組合提出了一種新的時頻分析方法,參數估計性能得到了提升,但是受噪聲影響大。文獻[12]在時頻分析基礎上引入門限降噪策略對噪聲進行抑制,提高了信號時頻參數估計性能,但是設置的靜態門限難以應對復雜動態變化的信號檢測場景。

考慮當前各類跳頻信號參數估計方法均存在各自不足,基于頻域互相關運算獲得相鄰時隙采樣信號的頻域互相關特征,通過引入邏輯回歸、門限自適應去噪算法完成對無人機遙控器信號參數的估計,提高了跳頻信號特征參數的估計性能。

1 信號模型與算法介紹

1.1 跳頻信號時域模型

小型無人機遙控器信號普遍采用跳頻通信技術,典型的跳頻信號時域模型[13]如下:

(1)

其中:

(2)

式(1)中的K為可觀測到的跳頻次數;ak(t)表示幅度;式(2)中,t′=t-(k-1)TH,sk(t)、fk、φk分別表示第k個跳頻信號分量及其瞬時載波中心頻率和初始相位;TH為每跳駐留時長。

在均值為0方差為σ2的復高斯白噪聲噪聲場景中,經過對信號離散采樣后的N點離散信號觀測值建模為

g(n)=s(n)+v(n),n=1,2,…,N

(3)

1.2 邏輯回歸算法

邏輯回歸分類器本質上是一組權值,與支持向量機、神經網絡等自主優化訓練的學習算法相比,其在模型訓練、預測耗時上都占有很大優勢。邏輯回歸模型[14]的數學表達式為

(4)

式中:θ為模型權值;x為輸入序列;f(θ;x)為模型預測的概率值,取值范圍為(0,1)。

根據實際需要設置閾值,通過判斷f(θ;x)是否超過閾值確定預測結果的所屬類別。利用最大似然方法對θ進行估算,它是一個高階可導的凸函數求解問題,本文中采用梯度下降法求最優解。

1.3 門限自適應算法

對離散信號g(n)進行傅里葉變換后得到G(n),則去噪算法的門限值[15]為

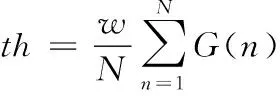
(5)

由于噪聲能量較小且分布在整個頻域范圍內,而跳頻信號的能量則相對比較集中,因此存在一個門限值能區分信號和噪聲,但是在不同場景下信號和噪聲的能量差異也不同,所以門限值是變化的,因此本文中引入門限自適應去噪算法去除噪聲。具體步驟如下:

1) 設定w在區間[1,10)以0.1為步長取值,并根據式(5)計算出門限值th(i),其中1≤i≤90。

2) 通過式(6)統計大于門限值th(i)的點數:

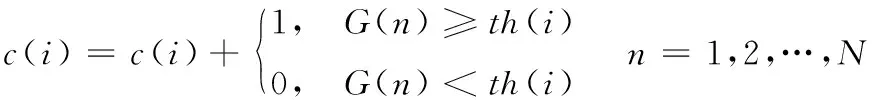
(6)

3) 計算c(i)二次差分結果中首次最接近零值的點,將其對應的權重w代入式(5)得到門限值。

2 小型無人機遙控器信號跳頻參數估計方法

同一架無人機遙控器信號的每跳信號具有相同帶寬,利用頻域互相關處理可在頻域上獲得高相似性的能量分布特征,因此基于該特性可以估計出無人機遙控器信號跳頻參數。為展示該特性,基于前文所述的跳頻信號模型生成仿真數據,設無人機遙控器信號的頻率范圍為10～250 kHz,頻率間隔為50 kHz,每跳信號駐留時長為10 ms,采樣頻率為900 kHz,采樣時長為500 ms,信號劃分時隙為1 ms,信噪比為9 dB。計算了無人機遙控器信號與噪聲的、相鄰跳信號的以及同一跳信號不同時隙的頻譜圖及其頻域互相關結果。

如圖1所示,當相鄰時隙信號的前一時隙和后一時隙分別為噪聲、信號時,兩者的頻域互相關結果不會出現明顯峰值,很顯然此時相鄰時隙信號不是同一跳無人機遙控器信號。圖2中,當相鄰時隙信號的前一時隙為前一跳信號的末段信號,后一時隙為后一跳信號的首段信號時,兩者的頻域互相關結果的峰值位置處于非0偏移頻點,雖然相鄰時隙信號均是無人機遙控器信號,但不屬于同一跳無人機遙控器信號。

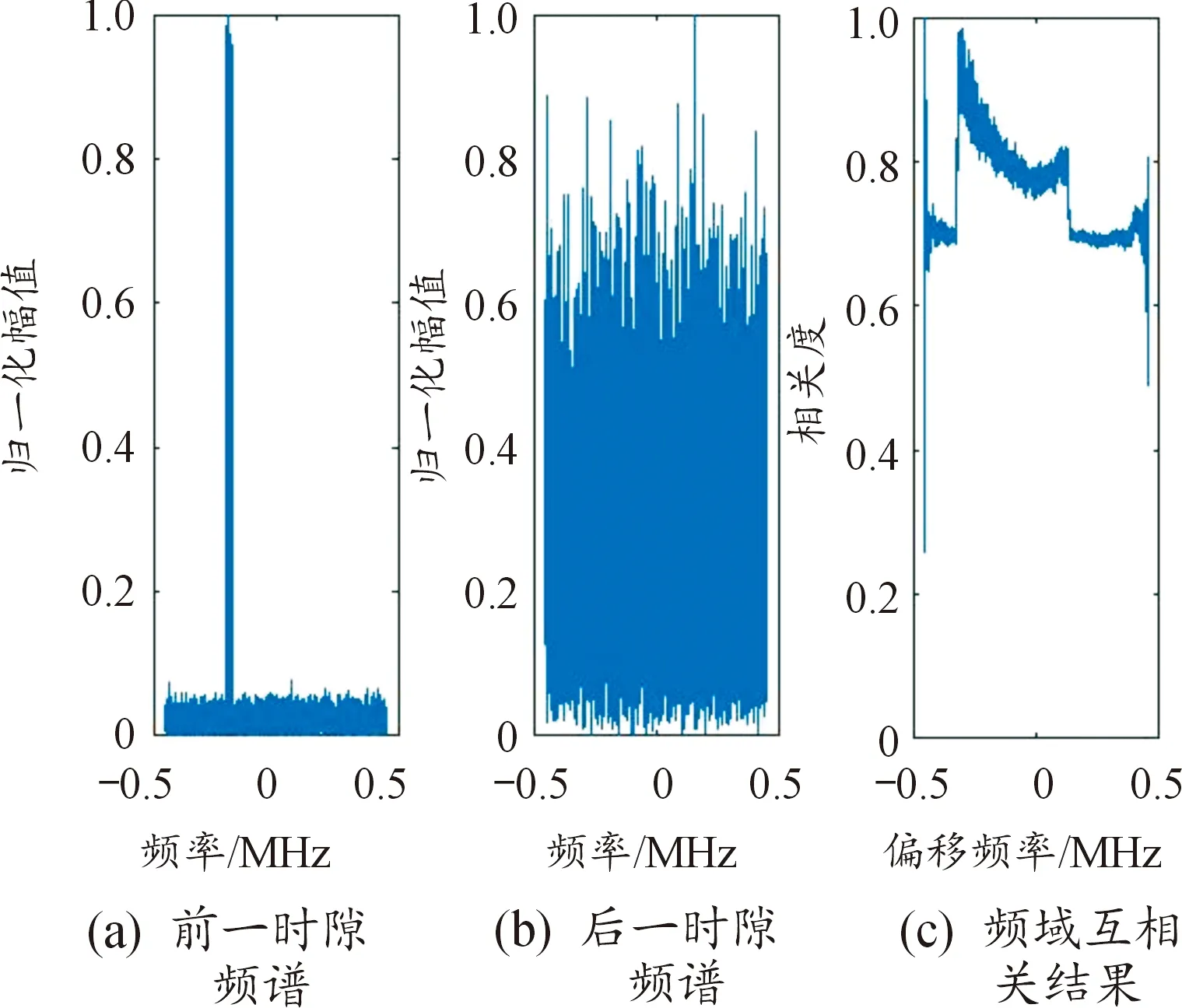
圖1 跳頻信號與噪聲的計算結果Fig.1 The calculation results of frequency hopping signal and noise

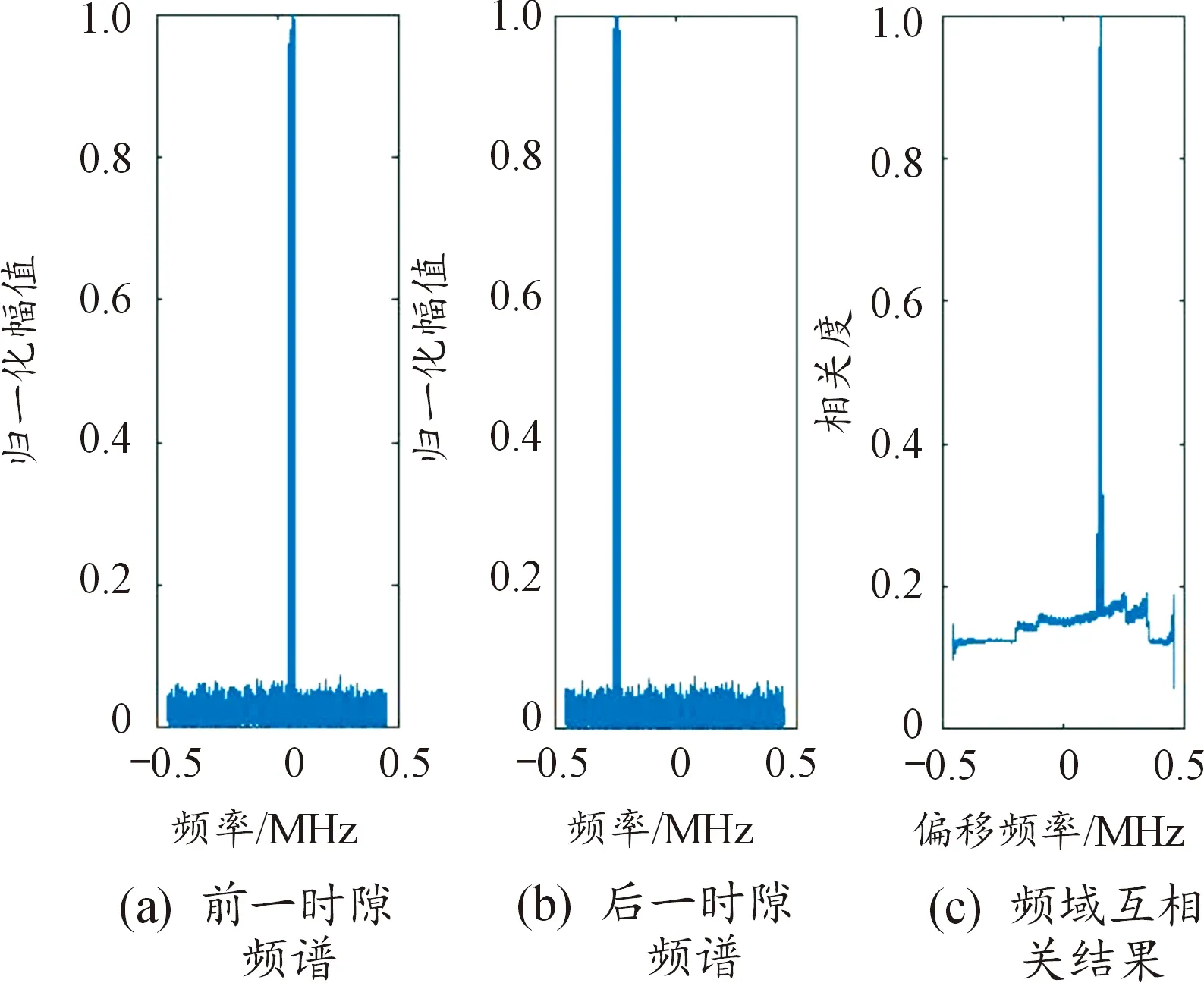
圖2 相鄰跳的跳頻信號計算結果Fig.2 The calculation result of adjacent hops of frequency hopping

從圖3的結果可以看到當相鄰時隙信號的前一時隙和后一時隙屬于同一跳信號相鄰時隙時,兩者的頻域互相關結果峰值處于0偏移頻點附近。

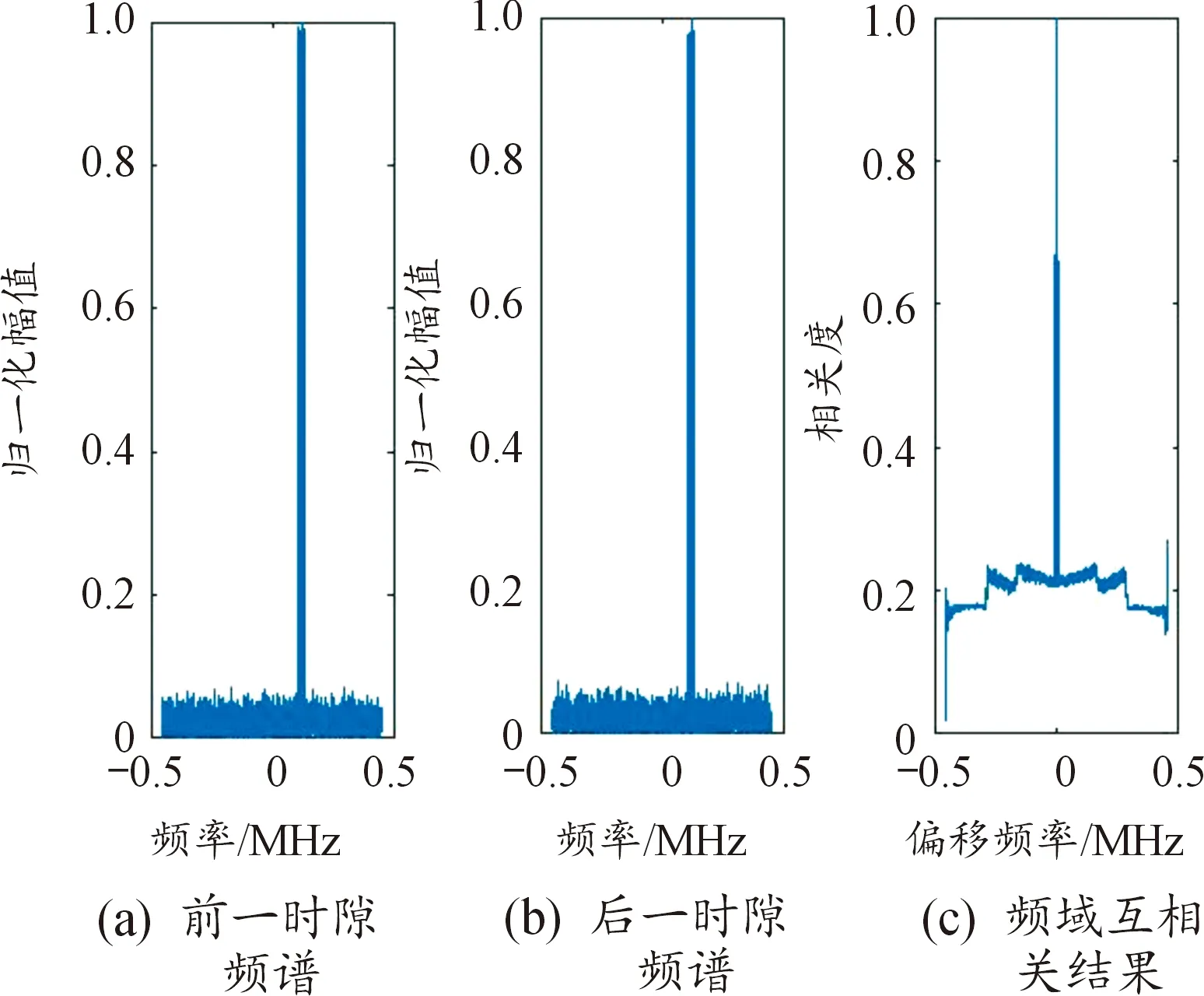
圖3 同一跳的跳頻信號計算結果Fig.3 The calculation result of the same hops of frequency hopping

基于此,本文中引入邏輯回歸算法對相鄰時隙信號的頻域互相關結果進行二分類,判斷相鄰時隙信號是否為同一跳信號從而估計出無人機跳頻信號的起跳時刻、每跳駐留時長等特征參數。然后根據這類特征參數以跳為單位分割信號并對每跳信號進行傅里葉變換,利用門限自適應去噪算法在頻域上對每一跳信號進行去噪處理,最后計算最大頻點值和最小頻點值的差值、均值得到每跳信號的帶寬、中心頻率。首先按如下步驟訓練邏輯回歸分類器。

1) 把信號劃分時隙轉換為單個時隙樣本點數L,并將信號g(n)劃分為N/L段,得到:

gm=[g((m-1)L+1),g((m-1)L+2),…,g(mL)],

m=1,2,…,N/L

(7)

2) 求每一時隙信號gm的傅里葉變換得到Gm并計算相鄰時隙信號的頻域互相關結果:

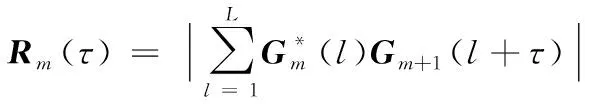
(8)

3) 生成訓練集。頻域互相關結果峰值處于零點位置附近的樣本設標簽為‘1’,否則設標簽為‘0’。

4) 將訓練集送入邏輯回歸分類器,經過訓練、迭代得到已訓練的分類器model。

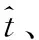
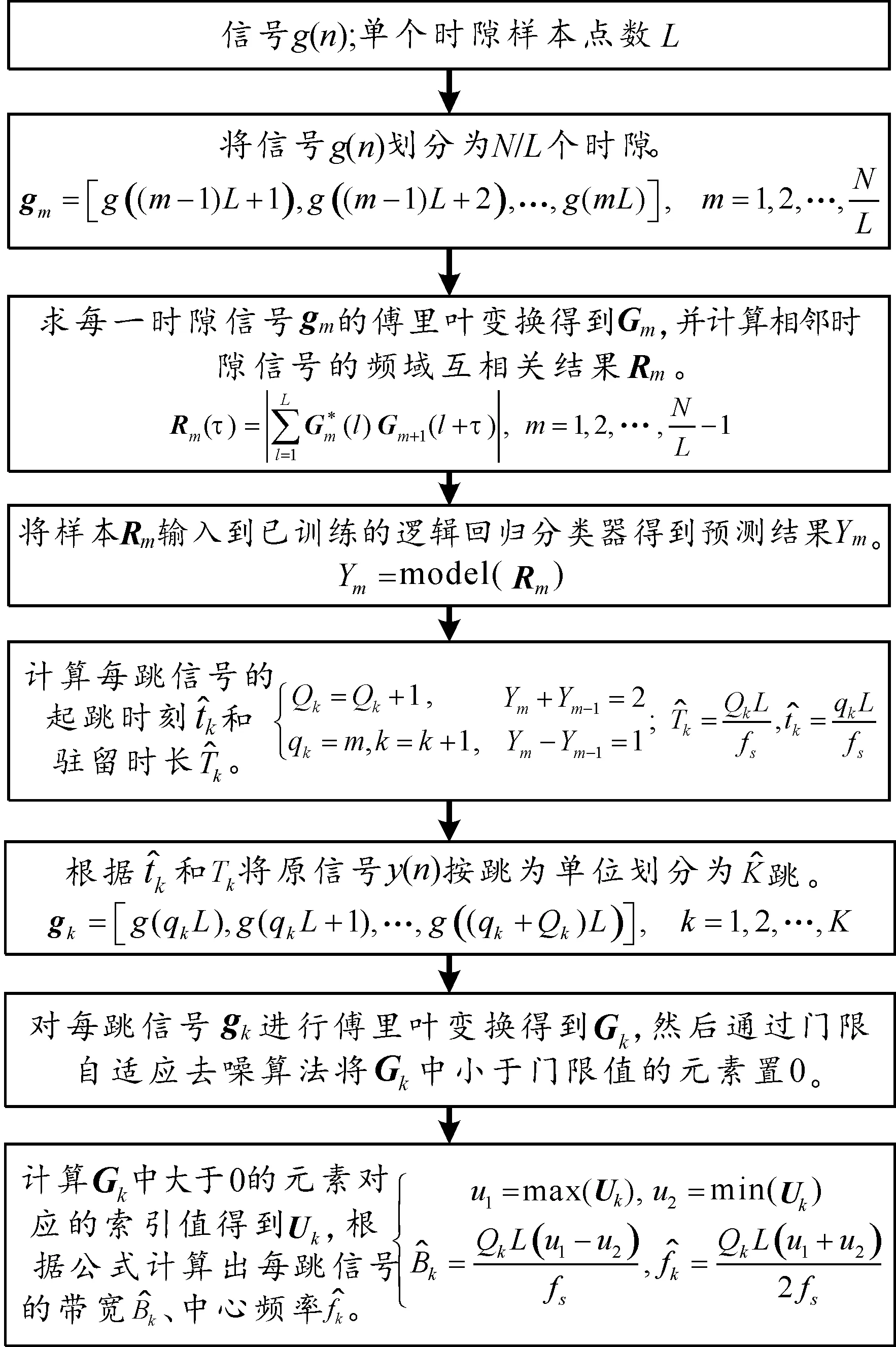
圖4 無人機遙控器信號參數估計流程圖Fig.4 The parameter estimation flowchart of the signal of UAV remote controller

值得注意的是,相同跳信號內的相鄰時隙信號具有較強的頻域互相關性,同時邏輯回歸算法在分類任務中具有運算速度快和準確度高的特點。因此在滿足相鄰時隙信號的頻域互相關這一前提下,單個時隙樣本點數L越小,所提方法對每跳信號的起跳時刻、駐留時長參數的估計就越準確,且所提方法能同時兼顧時間、頻率分辨力。

3 仿真實驗與分析

3.1 評價指標

為驗證所提方法的跳頻信號參數估計性能,引入基于時頻脊線的跳頻參數估計法、基于最大值圖的跳頻參數估計法作為對比方法1、對比方法2。同時,使用平均相對誤差(mean relative error,MRE)作為每跳駐留時長參數估計性能的評價指標:

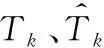
使用均方根誤差(root mean square error,RMSE)評價起跳時刻、每跳中心頻率估計性能:

(10)

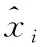
3.2 仿真實驗

通過仿真實驗對比分析小型無人機信號被完整采集時所提方法與傳統方法的參數估計性能。仿真場景:跳頻信號的頻率變化范圍為10～250 kHz,頻率間隔為50 kHz,每跳信號駐留時長為10 ms,采樣率為900 kHz,采樣時間為0.5 s。對信號加注信噪比變化范圍為-10～8 dB,步長為2 dB的高斯白噪聲,在每個信噪比場景下進行1 000次蒙特卡洛仿真實驗。

圖5和圖6的結果表明:對于每跳駐留時長和起跳時刻參數的估計:當信噪比達到2 dB時,對比方法的性能得到了小幅度的提升,誤差大約保持在10-3～10-4;信噪比達到2 dB后,所提方法擁有邏輯回歸算法的加持,在信噪比達到-2 dB時便得到了極大的提升并趨于穩定,誤差降低到了10-6左右。

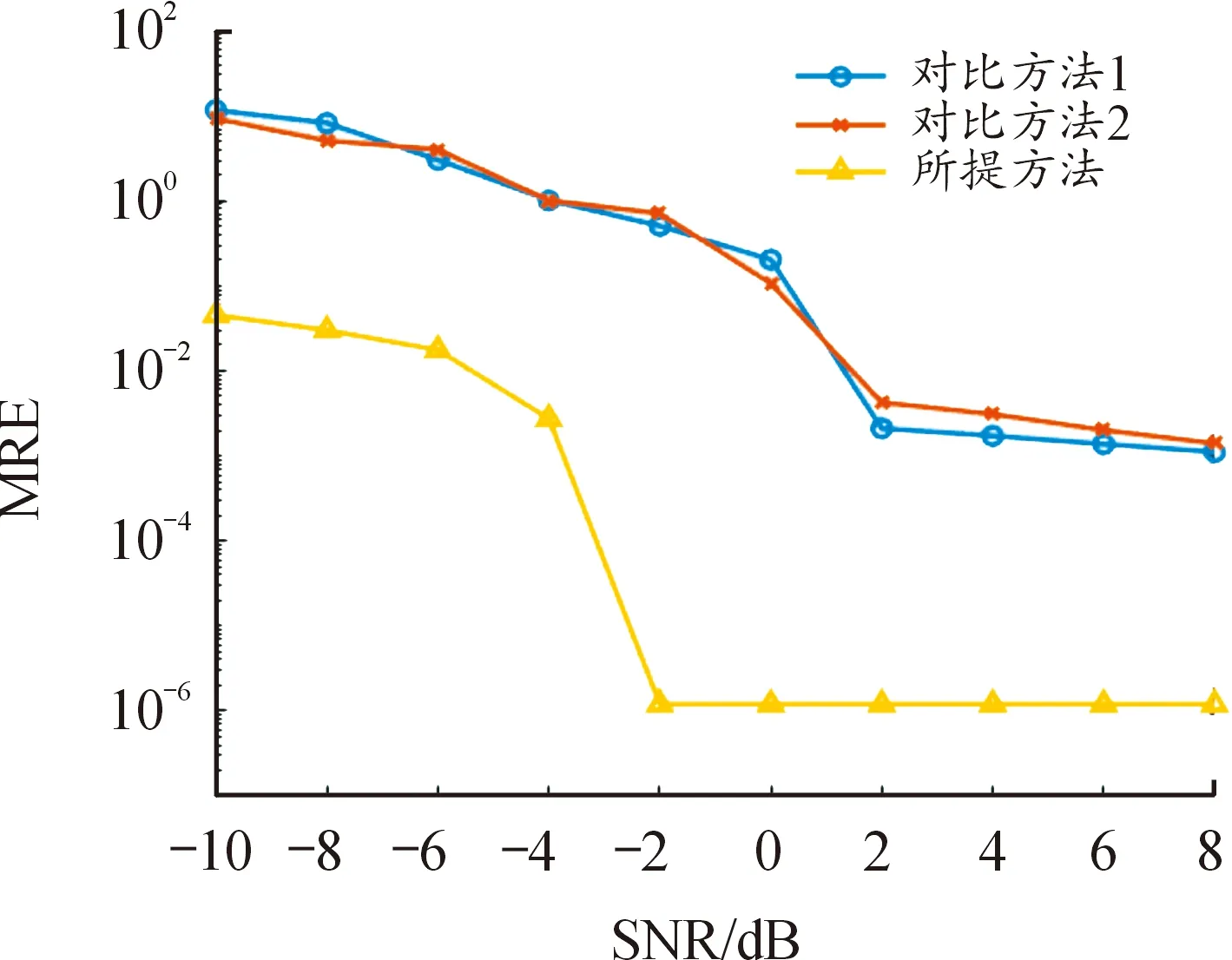
圖5 每跳駐留時長估計平均相對誤差Fig.5 MRE of estimated dwell time per hop

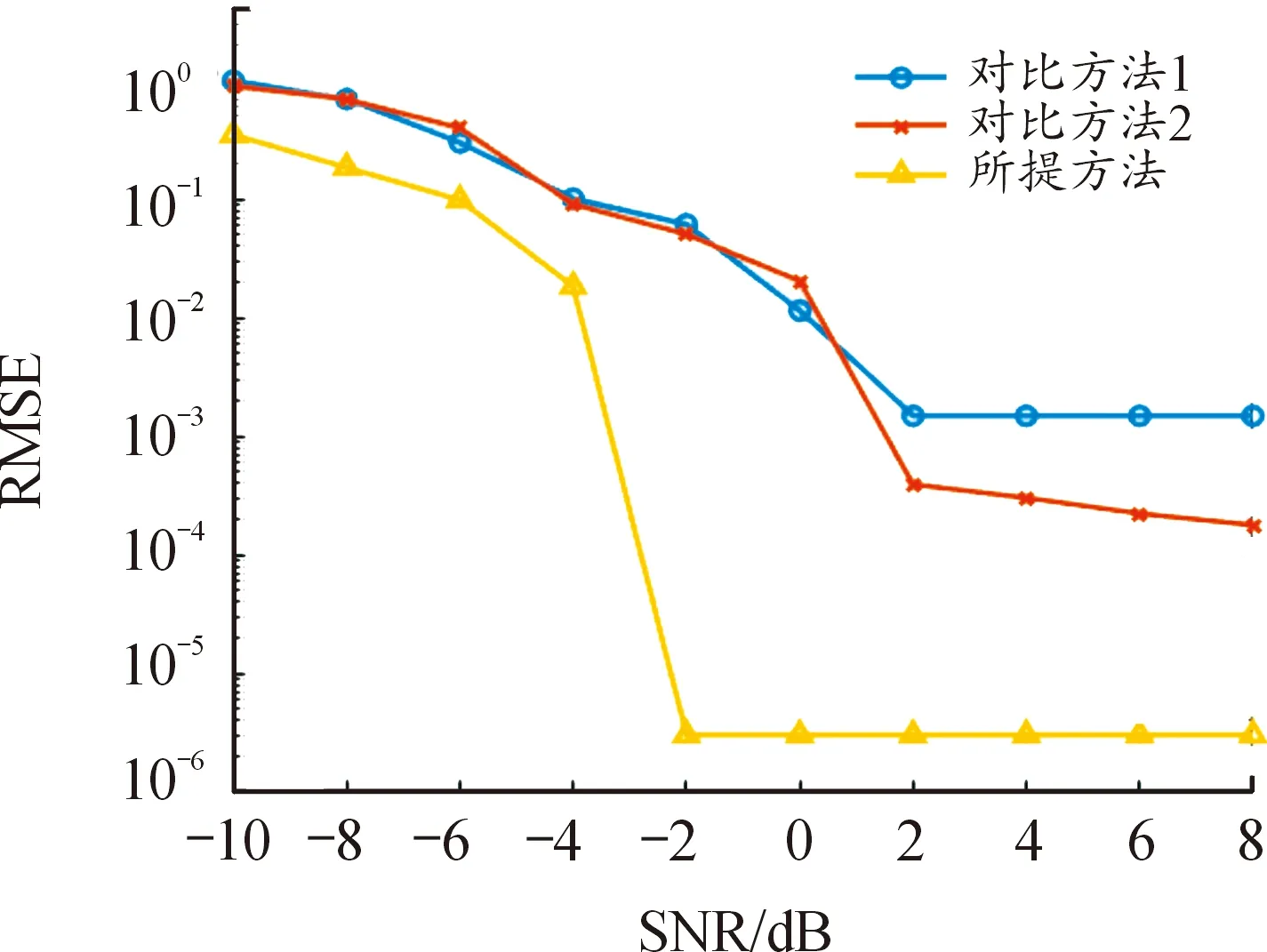
圖6 每跳起跳時刻估計均方根誤差Fig.6 RMSE of estimated frequency change time per hop

圖7為3種方法對每跳中心頻率參數估計的誤差結果。由于閾值的設定,傳統方法在極低信噪比下估計結果誤差較大,且隨著信噪比的增加參數估計性能的提升幅度較小,最小誤差在5×10-1左右。而所提方法引入了門限自適應去噪算法,性能得到了大幅提升,最小誤差大約為10-3。

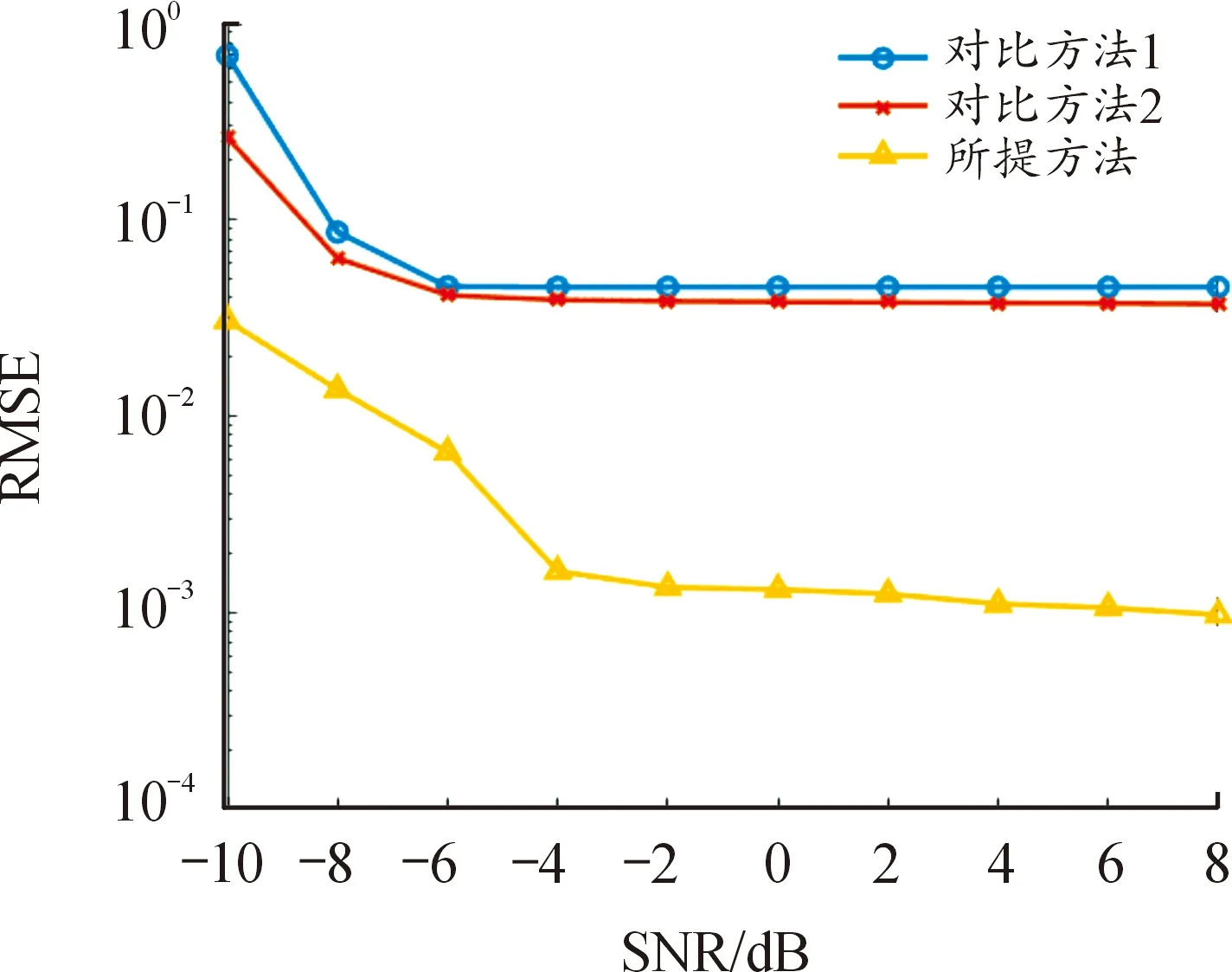
圖7 每跳中心頻率估計均方根誤差Fig.7 RMSE of estimated instantaneous center frequencyper hop

3.3 實驗分析

為驗證所提方法的可行性和有效性,進一步完成對實測數據的實驗分析。在微波暗室放置分布式智能頻譜傳感器、大疆精靈4無人機遙控器。將分布式智能頻譜傳感器的監聽范圍設置為2 410～2 420 MHz,數據采集平臺采樣率設置為10 MHz,采集時長為1 s。實驗設備如圖8所示。

圖8 分布式智能頻譜傳感器與無人機遙控器(左)、多通道數據采集板卡(中)、數據采集平臺(右)Fig.8 Distributed intelligent spectrum sensor and drone remote controller (left)、Multi-channel data acquisition board (middle)、Data collection platform(right)

信號采集設備采樣率小于無人機遙控器信號的跳頻總帶寬時無法完整地采集無人機遙控器信號,所采集的無人機遙控器信號在時域上具有不連續性。當某一時隙信號全是噪聲時,基于時頻脊線的跳頻參數估計法(即對比方法1)仍會將噪聲頻域信號的最大值對應的頻率值作為跳頻信號的瞬時頻率,這使得該方法不再適用,因此后續實驗舍棄了該方法。首先分別對接收信號的每跳駐留時長、起跳時刻、中心頻率參數進行100次測量實驗,并將各參數測量值的平均值作為后續實驗的真實值。然后對信號加注信噪比變化范圍為-12～15 dB,步長為3 dB的高斯白噪聲,在每個信噪比場景下進行1 000次蒙特卡洛實驗。

從圖9的每跳駐留時長估計平均相對誤差結果中可以得知,所提方法在信噪比極低的場景下性能優于對比方法2,并且在信噪比達到-6 dB時便得到了極大的提升并趨于穩定。圖10中起跳時刻估計均方根誤差結果反映出所提方法的參數估計性能全面優于對比方法2,這與仿真實驗的結果一致。

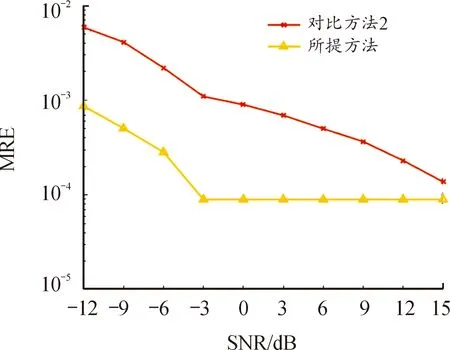
圖9 每跳駐留時長估計平均相對誤差Fig.9 MRE of estimated dwell time per hop

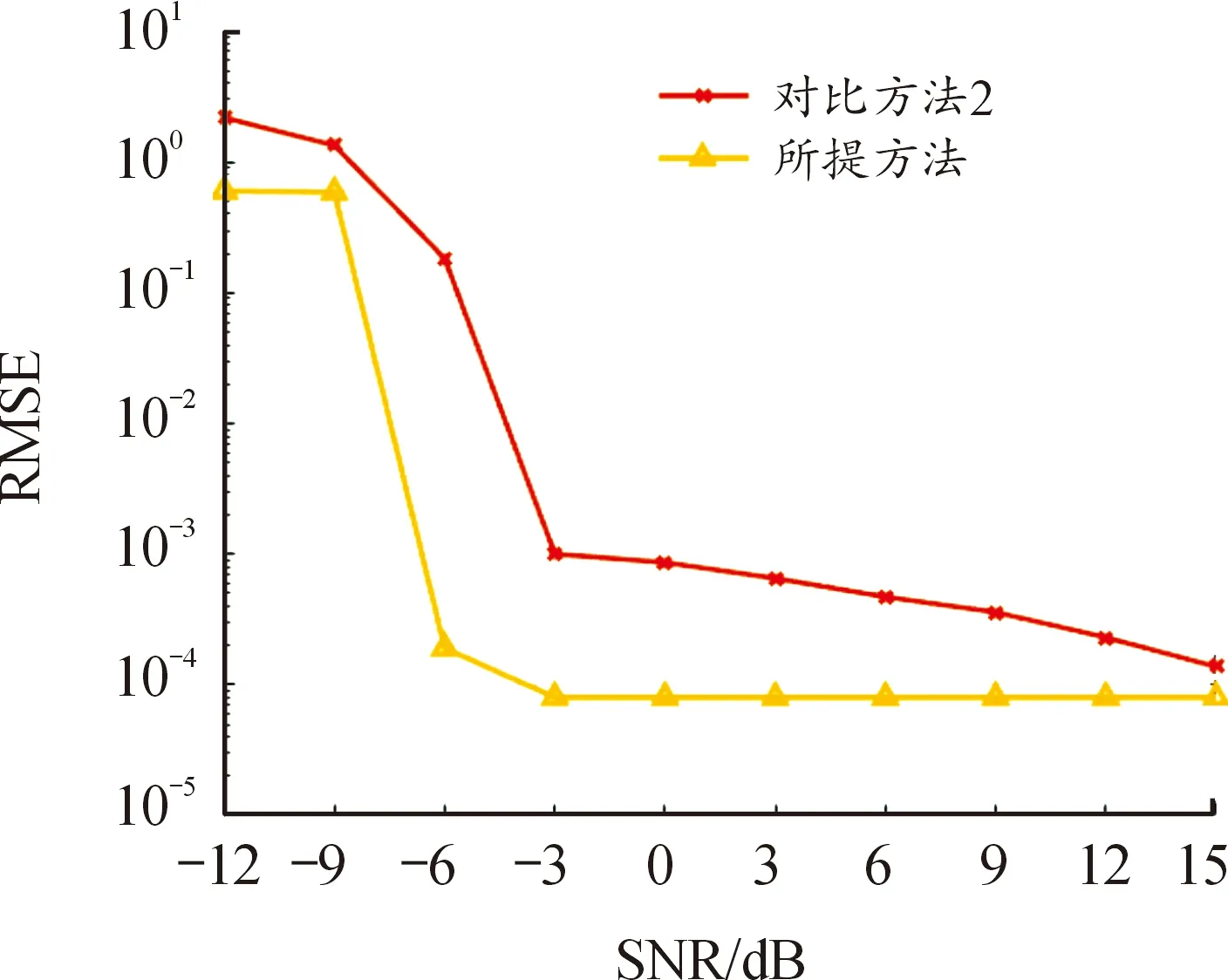
圖10 每跳起跳時刻估計均方根誤差Fig.10 RMSE of estimated frequency change time per hop

圖11為每跳中心頻率參數估計均方根誤差結果,在信噪比極低的場景下噪聲與信號的功率差異非常細微,無法通過門限值去除噪聲。但當信噪比達到-6 dB,噪聲與信號的功率差異逐步增大,門限自適應去噪算法能有效去除噪聲,提高參數估計性能。同時當信噪比大于-3 dB后,所提方法的參數估計性能趨于穩定且對噪聲的敏感度極低。

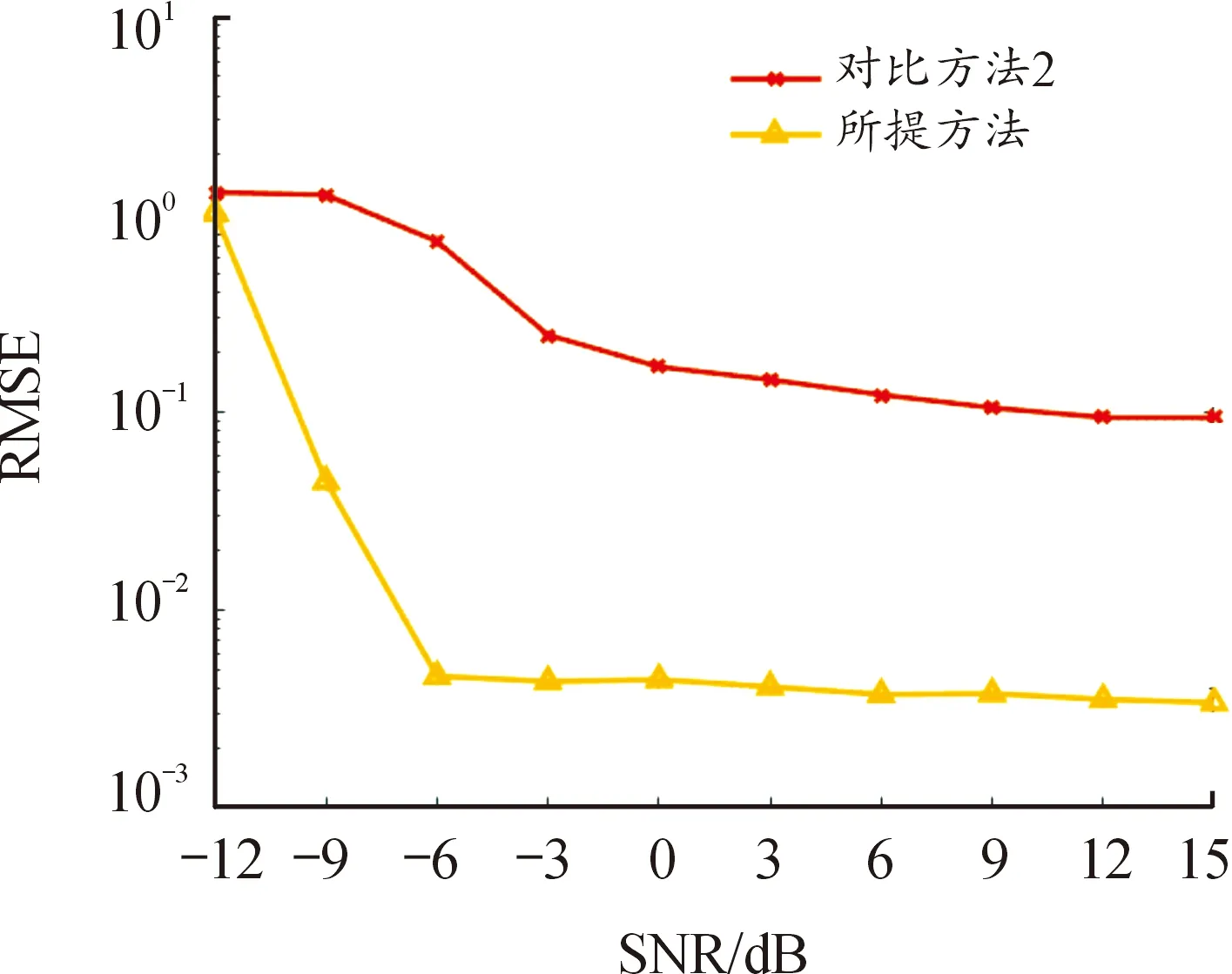
圖11 每跳中心頻率估計均方根誤差Fig.11 RMSE of estimated instantaneous center frequencyper hop

4 結論

通過引入邏輯回歸、門限自適應去噪算法提出了一種適用于估計時域連續和時域非連續跳頻信號參數的方法。并將該方法在仿真實驗和實測實驗中進行性能測試,得到以下結論:

1) 當信噪比達到-3 dB后,相鄰時隙信號的頻域互相關性逐漸提高,邏輯回歸算法能準確地判斷相鄰時隙信號是否屬于同一跳信號,因此所提方法對駐留時長、起跳時刻參數估計性能得到大幅提升。

2) 所提方法利用門限自適應去噪算法去除噪聲,然后估計出每跳信號的中心頻率。在信噪比達到-3 dB時對該參數的估計性能達到飽和,均方根誤差達到了10-2。

3) 在噪聲干擾下,所提方法的參數估計性能全面領先于傳統的時頻分析法。