PBX-9404炸藥臨界起爆特性數值模擬

栗丁丁,何中其

(南京理工大學, 南京 210094)

0 引言

隔板實驗是用于測定炸藥沖擊起爆特性的典型方法,利用臨界隔板值定性表征不同試樣的相對沖擊波感度大小。沖擊波感度是指在沖擊波作用下,炸藥發生爆轟的難易程度,是衡量炸藥安全性能的一個重要指標[1],為了能夠定量表征該臨界條件,很多人用沖擊波壓力表征試樣的沖擊起爆閾值[2-4],因此我們用臨界隔板厚度和臨界起爆壓力來描述試樣炸藥的臨界起爆特性。

在隔板實驗過程中,沖擊波會經過有機玻璃進入試樣炸藥,探究沖擊波在有機玻璃中的衰減規律,可以為試樣炸藥臨界起爆特性的研究奠定基礎,當然隔板材料的差異、試件殼體厚度的不同、點火方式的改變都會影響試樣炸藥的臨界起爆特性,有學者在這些方面做過研究,例如文獻[5]采用PVDF壓電式壓力傳感器測量了在平面波透鏡加載下經不同厚度有機玻璃隔板衰減后的沖擊波壓力歷程,結果表明沖擊波加載及裝置尺寸的不同,密實介質的衰減系數會有所差別;文獻[6]獲得了由有機玻璃與LY-12鋁合金組合的雙層介質隔板排序、總厚度與厚度分配對透射到被發炸藥中沖擊波各參量的影響規律,認為選取波阻抗遞增的排序時,透射沖擊波能量較低,對炸藥的安全性更有利。

模擬計算中,常常采用Lee-Tarver點火增長模型來描述試樣炸藥的沖擊起爆過程[7],但是對于PBX-9404炸藥,不同學者給出的Lee-Tarver參數存在一定的差異,這些模型參數是否適合來描述炸藥沖擊起爆過程還需與實驗進行對比驗證。

由于隔板實驗的零部件都是一次性的,做一次實驗需要更換一次實驗部件,不能做重復的實驗,因此做沖擊波起爆隔板實驗需要消耗大量的人力、物力、財力,這就使得采用實驗方法獲得的實驗數據非常有限且非常來之不易。目前對于PBX-9404炸藥的臨界起爆特性的研究鮮有報道,在數值模擬方面的研究也少之又少,因此本文采用數值模擬和文獻驗證的方法,對PBX-9404炸藥的臨界起爆特性問題進行探究。

1 數值計算模型

1.1 幾何模型

模型參考GJB772A—97中卡式隔板法的實驗裝置,按照實驗尺寸建立計算模型如圖1所示。圖1中,主發藥柱為鈍化黑索今(RDX)藥柱,藥柱尺寸為直徑40 mm、高度25 mm,密度為1 600 kg/m3;隔板材料為有機玻璃,隔板尺寸為直徑40 mm;試件殼體和見證板材料為鋼,尺寸分別為32 mm×26 mm×76 mm的鋼管和100 mm×100 mm×6 mm的鋼板;受發藥柱選擇PBX-9404炸藥,密度為1 842 kg/m3。

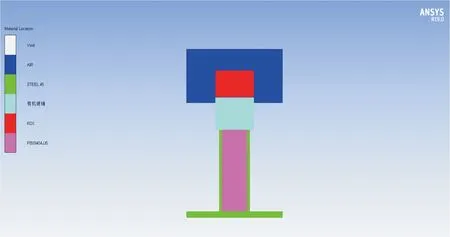
圖1 計算模型Fig.1 The calculation model

由于模型是軸對稱模型,因此建立二維模型更方便計算。主發藥柱RDX采用Euler算法,建立一個可以覆蓋RDX爆炸范圍的空氣計算域,其余部分采用Lagrange算法。歐拉網格尺寸0.67 mm×0.67 mm,拉格朗日網格尺寸0.5 mm×0.5 mm。通過join設置連接,連接隔板、試件殼體與驗證板,通過interaction設置接觸,隔板與試樣炸藥、試樣炸藥與試件殼體和驗證板的作用過程均采用Lagrange/Lagrange耦合算法計算。

1.2 材料模型

空氣材料采用IDEAL AIR狀態方程,其表達式為:

p=(γ-1)ρe-pshift

(1)

式中:P、γ、ρ、e和pshift分別為壓力、絕熱指數、密度、內能和初始壓力。

試件殼體材料和見證板采用材料庫里的Steel 4340,狀態方程選用Linear,強度模型采用Johnson-cook,失效模型基于Mott破片分布理論的Stochastic隨機破壞模型[8],失效準則為Principal Stress,Principal Tensile Failure Stress值取0.035 Mbar,侵蝕準則選用Geometric Strain,Erosion Strain值取1。強度模型表達式為:

(2)

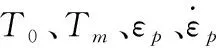
主發藥柱為RDX,狀態方程選用JWL EOS;隔板材料為有機玻璃,狀態方程采用shockEOS,具體模型參數見表1。

表1 RDX及有機玻璃的材料參數Table 1 Material parameters of RDX and Plexiglass

被發藥柱試樣PBX-9404炸藥在描述沖擊波起爆過程時采用Lee-Tarver三項式點火增長反應速率模型,即:

G1(1-λ)cλdpy+G2(1-λ)eλgpz

(3)

式中:λ、t、ρ分別為反應度、時間、密度;I、G1、G2、a、b、c、d、e、g、x、y和z這12個參數全部為常數。模型右邊第1項表示炸藥在沖擊壓縮作用下的熱點點火階段,當λ≥Fig max時該項為0;第2項表示熱點緩慢燃燒階段,當λ≥FG1 max時該項為0;第3項表示熱點合并后炸藥的快速反應階段,當λ≤FG2 min時該項為0。該方程與JWL方程有很好的相容性,通常配套使用。

采用JWLEOS來描述PBX-9404炸藥的未反應產物和爆轟產物的驅動膨脹過程,含溫度形式的JWL狀態方程形式為:

(4)

表2 PBX-9404炸藥未反應炸藥和爆轟產物JWL狀態方程參數Table 2 Parameters of JWL equation of state for unreacted explosives and detonation products of PBX-9404 explosives

1.3 Lee-Tarver反應速率參數的確定

由于PBX-9404炸藥在材料庫里有多組Lee-Tarver反應速率方程參數,為了研究炸藥Lee-Tarver模型參數對計算結果的影響,選取合適的模型參數來正確描述炸藥沖擊起爆過程,選取PBX-9404炸藥的3組不同Lee-Tarver模型參數[10-12],建立與文獻中實驗模型一樣的計算模型,分別計算這3種模型參數對應的臨界起爆速度,并將計算結果與文獻[13]中試驗結果對比。表3給出了本文選取的3組PBX-9404炸藥Lee-Tarver模型參數,表4為計算結果與試驗結果的對比,所得計算結果與文獻[14]稍有差別,可能是由于在設置材料的失效和侵蝕狀態方程時所取的參數值不同。

表3 PBX-9404炸藥的Lee-Tarver反應速率參數Table 3 Lee-Tarver reaction rate parameters of PBX-9404 explosive

從表4中可知:采用不同參數得到的計算結果相差較大,采用Bahl 1981反應速率參數計算得到的臨界起爆速度最接近實驗結果,相對誤差大概為3.75%,這說明該組參數可以很好的描述沖擊起爆炸藥一系列問題;采用Tarver 1981反應速率參數的計算結果與實驗結果相差較大,相對誤差約為19.65%;采用Tarver 1985的反應速率參數計算時,PBX-9404炸藥在很小的速度情況下依然能發生爆轟,所得計算值遠遠小于實驗結果,表明Tarver 1985參數不適合描述PBX-9404炸藥的沖擊起爆過程。

表4 參數計算結果與實驗結果對比Table 4 Parameter calculation results compared with experimental results

為了進一步驗證參數選取的準確性,采用上文的計算模型,用本文選取的3種Lee-Tarver反應速率參數對卡式隔板試驗進行數值模擬,計算結果如表5所示,在表5中,δr為臨界隔板厚度,Pr為臨界起爆壓力。

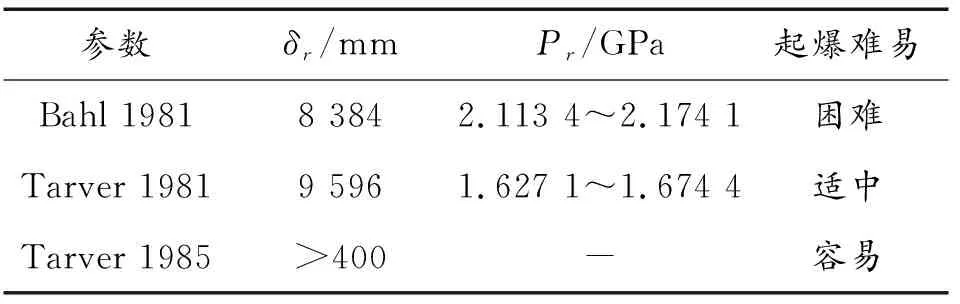
表5 不同參數隔板試驗計算結果Table 5 Calculation results of different parameters of diaphragm test

由上述對3種不同Lee-Tarver反應速率參數模擬計算的結果可知:本文選取的3種點火增長模型參數所得出的計算結果有一定的差異,尤其是選用Tarver 1985模型參數時,計算結果與其他2組參數相差太大。采用這3種參數來描述試樣炸藥沖擊起爆過程的計算結果與上面計算臨界速度閾值計算結果非常相似,從定性的角度談,臨界速度閾值和臨界隔板厚度一定程度上都可以反映被發試樣沖擊起爆的感度大小,臨界起爆速度越大,說明被發試樣越不容易被沖擊起爆,同樣地,臨界隔板值越小,則臨界起爆壓力越大,說明被發試樣越不容易被沖擊起爆。我們從定性的角度可以得出:按臨界起爆速度來排序,Bahl 1981>Tarver 1981>Tarver 1985;按照臨界起爆壓力來排序,Bahl 1981>Tarver 1981>Tarver 1985,并且Tarver 1985模型參數在描述2類沖擊起爆問題時表現出同樣的問題,在上文中模擬得出的計算結果與文獻實驗進行對比后確定了Lee-Tarver狀態方程參數,即采用Bahl 1981模型參數,這再一次印證了上文提到的選取模型參數的準確性。

因此,在數值模擬沖擊起爆炸藥時,模型參數的選取需謹慎。本文后續開展卡式隔板實驗沖擊起爆裝藥的數值模擬均采用Bahl 1981反應速率參數。

2 沖擊波在有機玻璃中衰減規律的研究

在計算PBX-9404炸藥沖擊起爆特性前,首先利用數值模擬方法對沖擊波在有機玻璃中的衰減規律進行研究,一方面能夠驗證數值模擬的準確性,另一方面還能夠進一步研究沖擊波在有機玻璃中傳播的其他特性,為進一步研究PBX-9404炸藥的沖擊起爆特性奠定基礎。

2.1 計算模型

沖擊波在有機玻璃中的衰減規律計算模型參照上面卡式隔板法的實驗模型建立,各個部分尺寸如圖2所示,具體材料參數見表1,具體算法尺寸參見上文。在軸向處每隔5 mm設置一個檢測點。

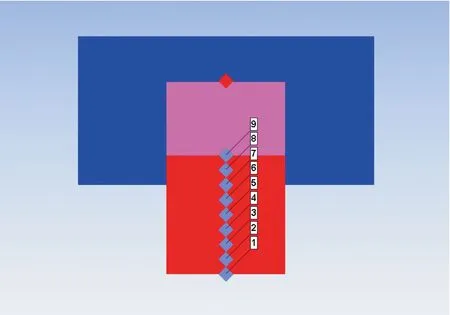
圖2 有機玻璃衰減模擬模型圖Fig.2 Plexiglass attenuation simulation model diagram

2.2 計算結果

通過數值模擬,我們可以清楚地觀察到沖擊波在有機玻璃中的動態傳播過程:主發藥柱RDX爆轟產生的沖擊波在3.0 μs時到達有機玻璃上表面,此時顯示的最大壓力值為18.96 GPa,通過觀察檢測點9我們得出它的入射沖擊波壓力為16.78 GPa;在3.0 μs后沖擊波開始在有機玻璃中傳播,可能是由于點起爆的原因,沖擊波前沿波陣面呈現一定的曲率向下傳播,隨著沖擊波逐漸往下傳播,沖擊波壓力值越來越小,有機玻璃的形變也越來明顯;在12.0 μs時,爆轟沖擊波到達有機玻璃下表面,可以判斷出沖擊波在有機玻璃中大概傳播了9.0 μs。有機玻璃不同位置的壓力分布圖如圖3所示。

將模擬得到的各個檢測點的沖擊波壓力峰值列于表6。從表6可以看出,隨著隔板厚度的增加,各個點的壓力峰值越來越低,逐漸減小,而且減小的速度越來越慢,也即減小的幅值逐漸降低,與文獻實驗結果對比發現數值相差不大。其中δg為隔板厚度,Pm為模擬結果壓力峰值,Ps為文獻[15]實驗結果壓力峰值。

表6 沖擊波壓力峰值計算值與實驗值比較Table 6 Comparison between calculated and experimental values of shock wave pressure peak

沖擊波壓力在密實介質中符合指數形的衰減規律為[16]:

P=ke-α.x

(5)

將式(5)兩邊取對數,可得:

lnp=lnk-α.x

(6)

即lnp與x呈線性關系,由表6中模擬數據擬合得出的lnp與x的關系曲線見圖4,擬合曲線得到的關系式為:

圖4 ln p與x的關系曲線Fig.4 The relationship between ln p and x

lnp=2.677-0.042x

將沖擊波壓力衰減情況的模擬結果與實驗結果進行對比,結果如圖5所示,可以看到這2條曲線吻合得較好。由圖5可知,數值模擬的初始壓力較文獻結果低約1 GPa,這可能是因為主發藥柱RDX的沖擊阻抗值ρD大于有機玻璃的沖擊阻抗值ρmDm,產物中反射波為稀疏波,界面上的壓力Px將比爆炸產生的爆轟波的C-J壓力PJ低,也即數值模擬的初始壓力計算結果較文獻實驗結果低。

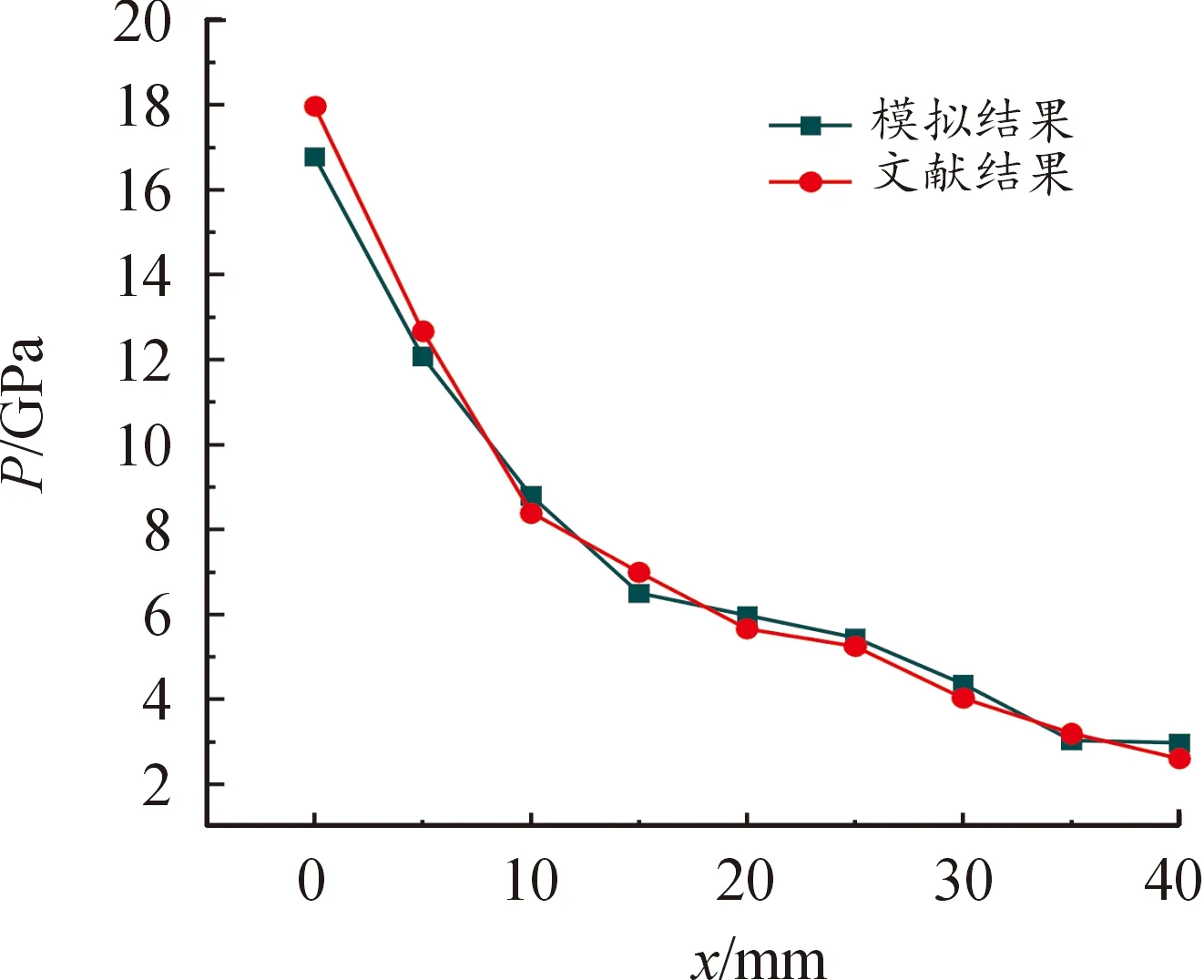
圖5 沖擊波壓力衰減情況的模擬結果與實驗結果對比Fig.5 Comparison of simulated and experimental results of shock wave pressure attenuation

采用式(5)、式(6)處理表中數據,可以得到不同位置壓力P與隔板厚度x的衰減規律關系式:P=14.55e-0.042.x。上式表明沖擊波壓力在有機玻璃直徑為40 mm的情況下的衰減系數值為0.042,與文獻中的0.05相差較小,說明模擬結果與實驗結果有較好的一致性,進一步驗證了數值模擬的準確性。

3 數值模擬結果及分析

由以上的數值模擬跟實驗的比較結果不難看出,數值模擬的準確性,數據與實驗結果基本吻合,也即采用該Lee-Tarver狀態方程參數能夠較好地描述PBX-9404炸藥沖擊起爆過程。接下來,通過改變一種條件、其他條件不變的控制變量法,研究PBX-9404炸藥的沖擊起爆特性,通過改變隔板材料、殼體厚度、點火方式3種方式來觀察對PBX-9404炸藥臨界起爆特性的影響規律。

在隔板實驗過程中主要是通過觀察底部見證板的凹痕程度來判斷試樣炸藥爆轟與否,而在數值模擬中主要通過觀察各個監測點的壓力時程曲線的峰值壓力的變化趨勢和反應度曲線的變化趨勢。若壓力峰值逐漸上升且達到試樣的爆轟壓力說明試樣發生爆轟,峰值壓力逐漸下降說明沒有發生爆轟;若反應度曲線斜率越來越大且最終達到1,則認為試樣發生爆轟,否則沒有發生爆轟。典型壓力波形圖如圖6所示,圖6(a)為沒有發生爆轟,圖6(b)為發生爆轟;典型反應度曲線波形圖如圖7所示,圖7(a)反應度曲線斜率越來越小且沒有達到1即未發生爆轟,圖7(b)為發生爆轟。

圖6 壓力時程曲線波形Fig.6 Pressure time history curve waveform

圖7 反應度曲線波形Fig.7 Responsiveness curve waveform

3.1 隔板材料對臨界起爆特性的影響

除了上文提到的有機玻璃外,還選擇了阻抗強度相差較大的鋁(AL6061-T6)和鋼(STEEL4340)作為隔板材料,分別進行數值模擬,來研究隔板材料對臨界起爆特性的影響。在模擬中采用隔板厚度步長為1 mm,根據上文提到的沖擊起爆的壓力峰值和反應度曲線作為判斷準則,來判斷試樣是否發生爆轟,表7為數值模擬得到的計算結果,其中ρD代表隔板材料的沖擊阻抗值[17]。

表7 臨界起爆特性數值模擬的計算結果Table 7 Calculation results of numerical simulation of critical detonation characteristics

從表7可以看出,臨界隔板厚度小的沖擊阻抗大,臨界隔板厚度大的沖擊阻抗小。鋼的臨界隔板厚度最小,沖擊阻抗最大,有機玻璃的臨界隔板厚度最大,沖擊阻抗最小,兩者的隔板值相差較大,這是由于沖擊波在鋼板中的衰減程度最高,在機玻璃中的沖擊波衰減程度相對低。還可以看出,雖然隔板材料不同,但由于試樣炸藥和試件殼體材料都不變,PBX-9404炸藥的臨界起爆壓力差別不是很大。

3.2 殼體厚度對臨界起爆特性的影響

為了得到不同試件殼體厚度對PBX-9404炸藥臨界起爆特性的作用規律,在其他條件不變的情況下,隔板材料依然選擇有機玻璃,我們分別選取17 mm筒壁厚度的鋼管作為試件殼體,厚度步長為1 mm,殼體厚度對臨界隔板厚度和臨界起爆壓力的關系如圖8所示。圖8中黑色方形曲線反映殼體厚度與臨界隔板厚度的關系,紅色圓點形曲線反映殼體厚度與臨界起爆壓力的關系,為殼體厚度。

從圖8中可以看出,當殼體厚度為1 mm時,促使炸藥發生爆轟的臨界隔板厚度為79～80 mm,對應的臨界起爆壓力為2.303 9～2.357 0 GPa,隔板厚度大于此值或起爆壓力小于此值,試樣炸藥都不會發生爆轟,當殼體厚度為2 mm時,臨界隔板厚度為82～83 mm,對應的臨界起爆壓力為2.174 1～2.213 0 GPa,同樣地,當殼體厚度為3 mm時,臨界隔板厚度為83～84 mm,對應的臨界起爆壓力為2.113 4～2.174 1 GPa。從圖8中正方形點曲線可知:PBX-9404炸藥的臨界隔板厚度隨著試件殼體厚度的增加逐漸增加,但當殼體厚度增加到5 mm時,臨界隔板厚度增長到86～87 mm,此后不再發生改變;從圓點形曲線可知:臨界起爆壓力隨殼體厚度的曲線變化正好與臨界隔板值隨殼體厚度的曲線變化相反,這說明增加試件殼體厚度可以更容易的使試樣炸藥發生爆轟,同樣的,當試件殼體厚度增加到5 mm時,臨界起爆壓力為1.999 4～2.036 7 GPa,此后在隨著殼體厚度的增加,起爆壓力的臨界值雖然稍有浮動,但大致趨于2.03 GPa。

圖8 殼體厚度對臨界隔板厚度和臨界起爆壓力的影響Fig.8 Influence of shell thickness on critical diaphragm thickness and critical initiation pressure

產生這種現象的原因與試件殼體側向的稀疏波有關。 C.M.Tarver、P.A.Urtiew和K.Bahl等[18-19]對LX-04、LX-17藥柱在沒約束和弱約束下的沖擊感度進行了研究,認為弱約束下的沖擊感度較沒約束時有所增加,并作出了相應的解釋。增加殼體厚度,爆轟波延徑向傳播的難度增大,阻礙了試樣爆轟產物徑向做功的能力,減小了徑向能量損失,使得試樣炸藥爆轟產物有更多的能量來推動爆轟波的傳遞,從而使得試樣更加容易發生爆轟,也即增加試件殼體厚度可以使試樣爆轟更加容易。

3.3 起爆方式對臨界起爆特性的影響

除了隔板材料、殼體厚度的差異會對PBX-9404炸藥的臨界起爆特性有所影響,點火方式的不同也是一個重要的影響因素。在AUTODYN軟件中通過Detonation選項分別設置點起爆、環起爆、面起爆,圖9為不同起爆方式下起爆點示意圖,內部區域為RDX藥柱,外部為整個空氣計算域,紅色部分為起爆點。

圖9 不同起爆方式起爆點示意圖Fig.9 Schematic diagram of the detonation point of different detonation methods

在數值模擬軟件中分別采用中心點、環和面起爆3種方式對RDX進行點火,數值模擬結果如表8所示。

表8 起爆方式對臨界起爆特性的影響Table 8 Influence of detonation mode on critical detonation characteristics

由表8可知,采用點起爆時,臨界隔板值最小,采用面起爆時,臨界隔板值最大。在這3種起爆方式中,面起爆的臨界起爆壓力略小,但都趨于2.1 GPa左右。可以推斷出,改變起爆方式可以使反應更加完全,從而爆轟產物產生的壓力值能更好地通過有機玻璃隔板,即面起爆下反應更加完全,采用該方式下的臨界隔板厚度最大。

4 結論

本文采用數值模擬與文獻驗證的方法,應用AUTODYN軟件與點火增長模型模擬計算PBX-9404炸藥的臨界起爆特性,主要得出以下結論:

1) 在本文選取的3種Lee-Tarver模型參數中,Bahl 1981的反應速率參數可以更好地描述PBX-9404炸藥的沖擊起爆過程,使用該模型參數下的臨界隔板厚度為83～84 mm,臨界起爆壓力為2.113 4～2.174 1 GPa;

2) 沖擊波在有機玻璃中傳播規律的數值模擬中發現,不同位置壓力P與隔板厚度x的衰減規律關系式為P=14.55e-0.042.x,衰減系數值為0.042,與文獻中的0.05比較近接,再一次驗證了數值模擬的可靠性;

3) 通過改變隔板材料,得出鋼的臨界隔板厚度最小,沖擊阻抗最大,有機玻璃的臨界隔板厚度最大,沖擊阻抗最小,但臨界起爆壓力相差不大;通過改變試件殼體厚度,隨著試件殼體厚度的增加,炸藥的臨界隔板厚度逐漸增加,臨界起爆壓力逐漸減小,當殼體厚度增加到5 mm時,此后在隨著殼體厚度的增加,兩者不再發生變化;通過改變起爆方式,面起爆時臨界隔板值最大,點起爆最小。