一道教材習(xí)題的演變

李夢(mèng)娜

方程是刻畫(huà)現(xiàn)實(shí)世界數(shù)量關(guān)系的有效模型，能夠解決數(shù)學(xué)與實(shí)際生活中的問(wèn)題，也是中考重點(diǎn)考查的知識(shí)點(diǎn)之一。這類(lèi)題綜合性強(qiáng)，常常由教材習(xí)（例）題演變而來(lái)，現(xiàn)舉一例供同學(xué)們參考。

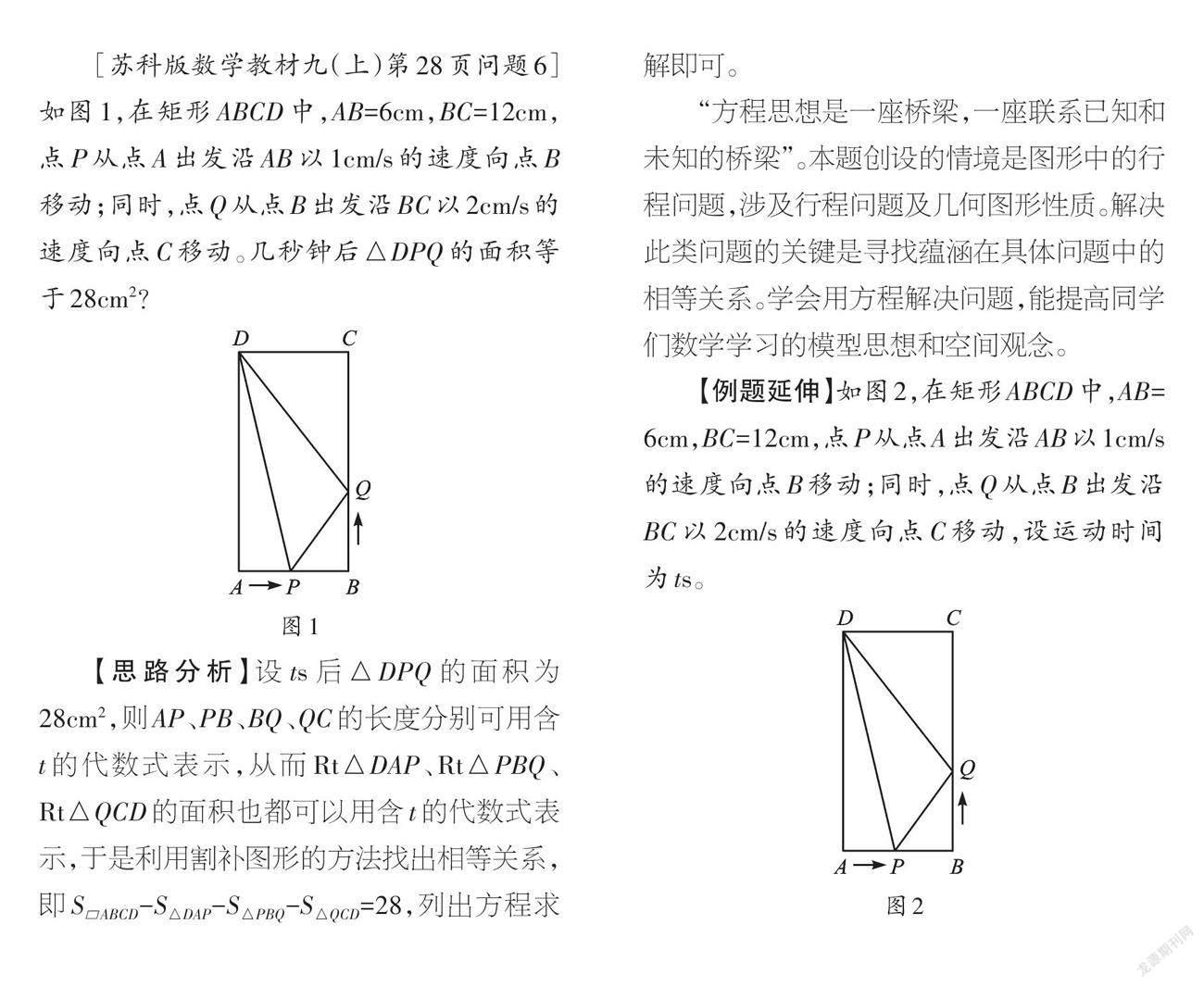
［蘇科版數(shù)學(xué)教材九（上）第28頁(yè)問(wèn)題6］如圖1，在矩形ABCD中，AB=6cm，BC=12cm，點(diǎn)P從點(diǎn)A出發(fā)沿AB以1cm/s的速度向點(diǎn)B移動(dòng)；同時(shí)，點(diǎn)Q從點(diǎn)B出發(fā)沿BC以2cm/s的速度向點(diǎn)C移動(dòng)。幾秒鐘后△DPQ的面積等于28cm2？

【思路分析】設(shè)ts后△DPQ的面積為28cm2，則AP、PB、BQ、QC的長(zhǎng)度分別可用含t的代數(shù)式表示，從而Rt△DAP、Rt△PBQ、Rt△QCD的面積也都可以用含t的代數(shù)式表示，于是利用割補(bǔ)圖形的方法找出相等關(guān)系，即S?ABCD-S△DAP-S△PBQ-S△QCD=28，列出方程求解即可。

“方程思想是一座橋梁，一座聯(lián)系已知和未知的橋梁”。本題創(chuàng)設(shè)的情境是圖形中的行程問(wèn)題，涉及行程問(wèn)題及幾何圖形性質(zhì)。解決此類(lèi)問(wèn)題的關(guān)鍵是尋找蘊(yùn)涵在具體問(wèn)題中的相等關(guān)系。學(xué)會(huì)用方程解決問(wèn)題，能提高同學(xué)們數(shù)學(xué)學(xué)習(xí)的模型思想和空間觀念。

【例題延伸】如圖2，在矩形ABCD中，AB=6cm，BC=12cm，點(diǎn)P從點(diǎn)A出發(fā)沿AB以1cm/s的速度向點(diǎn)B移動(dòng)；同時(shí)，點(diǎn)Q從點(diǎn)B出發(fā)沿BC以2cm/s的速度向點(diǎn)C移動(dòng)，設(shè)運(yùn)動(dòng)時(shí)間為ts。

（1）當(dāng)t=2時(shí)，△DPQ的面積為 cm2；

（2）在運(yùn)動(dòng)過(guò)程中，△DPQ的面積能否為26cm2？如果能，求出t的值，若不能，請(qǐng)說(shuō)明理由；

（3）運(yùn)動(dòng)過(guò)程中，當(dāng)A、P、Q、D四點(diǎn)恰好在同一個(gè)圓上時(shí)，求t的值；

（4）運(yùn)動(dòng)過(guò)程中，當(dāng)以Q為圓心、QP為半徑的圓，與矩形ABCD的邊共有4個(gè)交點(diǎn)時(shí)，直接寫(xiě)出t的取值范圍。

【思路分析】第（1）問(wèn)，根據(jù)運(yùn)動(dòng)速度和時(shí)間表示出線段長(zhǎng)度，然后計(jì)算出三個(gè)直角三角形的面積，再用割補(bǔ)圖形的方法就能得到△DPQ的面積，這一問(wèn)與教材上的問(wèn)題所用方法完全相同；……