波紋腹板幾何參數(shù)對軸壓比的影響

曹會敏，余浩銘，劉洪兵

（1.西北工業(yè)大學(xué)，陜西 西安 710072；2.西安交通工程學(xué)院，陜西 西安 710300）

0 引言

波紋腹板鋼是一種在一定條件下相較于普通H 型鋼構(gòu)件受力更優(yōu)越且更加節(jié)省鋼材的新型鋼材，近年來受到廣大科研工作者的關(guān)注[1-2]。國內(nèi)在建筑領(lǐng)域關(guān)于波紋腹板鋼的研究多集中在力學(xué)性能如抗剪、抗彎、疲勞、穩(wěn)定性等方面，而動力學(xué)性能的研究多集中在橋梁領(lǐng)域如孫鵬輝[3]利用ABAQUS 有限元軟件研究腹板傾斜角度對主梁動力特性的影響規(guī)律。戚偉利[4]采用大型通用有限元軟件Midas/Civil 建立模型，通過設(shè)置不同位置及不同數(shù)量橫系梁進(jìn)行動力特性分析。馮文章[5]根據(jù)箱梁截面抗剪能力相等原則，建立了波紋鋼腹板連續(xù)剛構(gòu)橋和相應(yīng)的混凝土腹板連續(xù)剛構(gòu)橋有限元模型，對二者的動力特性和抗震性能進(jìn)行了對比分析。基于此，筆者與其他研究人員從2016 年展開了對波紋鋼在建筑領(lǐng)域動力特性的研究，并于2018 年發(fā)表了波紋腹板H 型鋼框架結(jié)構(gòu)動力特性分析[6]，通過對比波紋腹板鋼結(jié)構(gòu)和普通鋼結(jié)構(gòu)的動力特性及分析地震波作用下兩種結(jié)構(gòu)的反應(yīng)特點發(fā)現(xiàn)波紋腹板鋼框架結(jié)構(gòu)的剛度與抗震性能都優(yōu)于普通H 型鋼。由于構(gòu)件的動力性能與構(gòu)件的軸壓比密切相關(guān)，本文將繼續(xù)研究波紋腹板H 型鋼構(gòu)件幾何參數(shù)對軸壓比的影響，為后期此類構(gòu)件在動力特性方面的進(jìn)一步研究提供理論依據(jù)。

1 模型及假定

1.1 模型創(chuàng)建

模型基于ABAQUS軟件創(chuàng)建，采用C3D8R實體單元，鋼材本構(gòu)模型見圖1，材料參數(shù)見表1，圖2 腹板波折參數(shù)示意圖，表2 為構(gòu)件參數(shù)對照。模型構(gòu)件一端施加荷載一端完全固定，加載方式見圖3 與圖6。

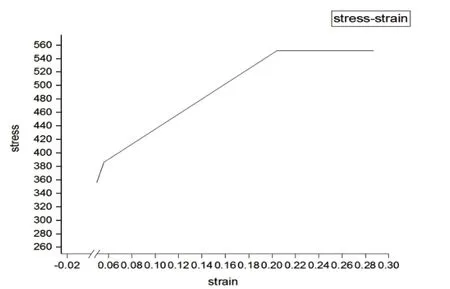
圖1 材料本構(gòu)模型

圖2 腹板波折參數(shù)

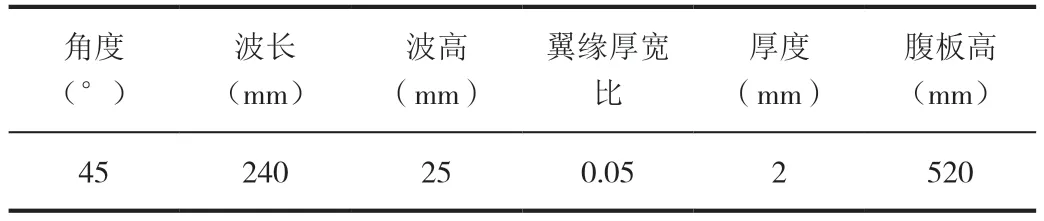
表1 材料參數(shù)

表2 構(gòu)件幾何參數(shù)對照表

1.2 計算假定

由于波紋腹板構(gòu)件在軸壓力作用下翼緣承擔(dān)了幾乎所有的力，而腹板基本不起作用，因此本文軸壓比計算假定抗剪滿足要求，不考慮腹板發(fā)揮的作用，利用n=計算，其中N 為軸向壓力值，Af為翼緣凈面積，f 為鋼材抗拉強度設(shè)計值。

2 荷載作用下軸壓比對構(gòu)件的影響

在討論幾何參數(shù)對軸壓比的影響前，先來觀察結(jié)構(gòu)在不同軸壓比時結(jié)構(gòu)的破壞特點與規(guī)律，以下給出了構(gòu)件在不同軸壓比時的破壞云圖、荷載位移曲線和應(yīng)力應(yīng)變曲線。

2.1 軸壓荷載作用

由于軸壓力作用時，若荷載直接加載在腹板上可能會導(dǎo)致局部應(yīng)力集中使變形較大，因此，將梁的兩端封閉起來作為剛性加載板如圖所示，加載方式如圖3 所示。

圖3 軸心荷載加載圖

由表3 可知，波紋腹板H 型鋼構(gòu)件兩翼緣的應(yīng)力隨著軸壓比的增加逐漸增加，直到構(gòu)件達(dá)到強度極限值而無法再承擔(dān)荷載的增加時破壞。此時腹板應(yīng)力值的增加較為緩慢，直到翼緣出現(xiàn)塑性鉸發(fā)生破壞時腹板的應(yīng)力值依然很小，說明在軸壓比達(dá)到某一值之前構(gòu)件的腹板不會破壞。由PEEQ 云圖可以看出，構(gòu)件腹板與翼緣連接處的應(yīng)變值偏大，與Mises 應(yīng)力圖結(jié)論基本一致，構(gòu)件的破壞主要是翼緣和翼緣與腹板的連接點附近的破壞。

表3 各軸壓比作用下構(gòu)件的破壞形式

當(dāng)軸壓比為0.8 時材料單元開始屈服，但未達(dá)到構(gòu)件的破壞應(yīng)變0.204。隨著軸力的增加塑性區(qū)逐漸增大，當(dāng)軸壓比在1.6與2 之間的某個值時構(gòu)件發(fā)生破壞。此變化過程中，腹板與翼緣接觸附近區(qū)域破壞較嚴(yán)重。

由圖4 荷載位移曲線可知：荷載達(dá)到1 388kN 附近時，荷載位移曲線是一條直線，因此可知1 388kN 附近的某個值是該構(gòu)件的彈性極值點，此時近似認(rèn)為1 388kN 為構(gòu)件的彈性極值點。圖5 得出的應(yīng)力應(yīng)變曲線完整地反映了構(gòu)件整個破壞過程，該曲線符合一般應(yīng)力應(yīng)變曲線的變化規(guī)律。彈性段為符合胡克定律的直線段，由各軸壓比值對應(yīng)得出的彈性極限值求平均值可得到彈性極限值約為1 313.557kN，此時彈性極值點對應(yīng)的軸壓比為1.059。因此，軸心壓力作用時，構(gòu)件的軸壓比值已超過了1。此時荷載位移曲線彈性極值點對應(yīng)的軸壓比n=1.12。兩種曲線得出的軸壓比值相差很小，說明荷載位移曲線與應(yīng)力應(yīng)變曲線得出的結(jié)論一致。

圖4 荷載位移曲線

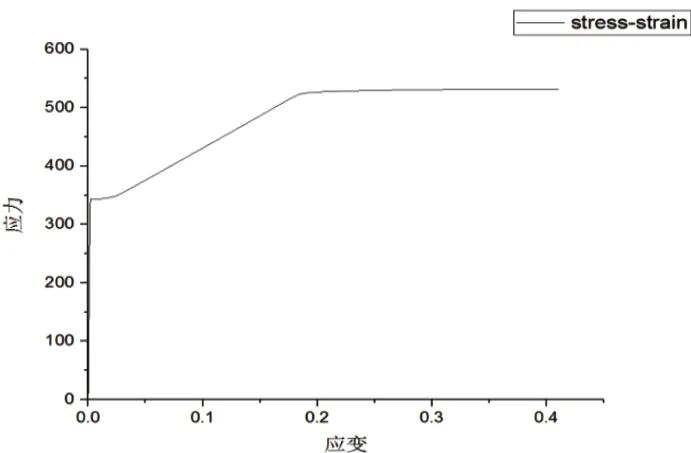
圖5 應(yīng)力應(yīng)變曲線

2.2 偏壓荷載作用

由軸壓荷載作用分析可知，軸壓作用下荷載的彈性極值約為1 313kN。經(jīng)過大量分析可知，當(dāng)結(jié)構(gòu)構(gòu)件受偏壓荷載1 300kN 時可出現(xiàn)結(jié)構(gòu)破壞的整個過程，因此構(gòu)件施加此荷載便可得到本節(jié)研究所需的數(shù)據(jù)。加載方式如圖6 所示。

圖6 偏心荷載加載圖

此處設(shè)：a=偏心距/腹板高度

表4 偏心荷載作用下構(gòu)件的破壞

通過比較a=0.25 與a=0.5 時構(gòu)件的Mises 云圖、PEEQ云圖與位移云圖可得，結(jié)構(gòu)構(gòu)件在荷載作用位置不同時的破壞特點基本一致。首先是離荷載較近一側(cè)的翼緣應(yīng)力值急劇增加，隨后另一側(cè)翼緣的應(yīng)力也開始增加，隨著荷載不斷增加，離荷載較近一側(cè)的翼緣首先破壞，緊接著腹板也逐漸不能承受荷載的增加而破壞，但此時離荷載較遠(yuǎn)一側(cè)翼緣的應(yīng)力反倒不再增加。說明此時構(gòu)件已不能再承受荷載的作用。

當(dāng)a=0.25 時，由荷載位移曲線與應(yīng)力應(yīng)變曲線可得，構(gòu)件的彈性極限承載力值約為872kN，此時對應(yīng)的軸壓比n1=0.703。當(dāng)a=0.5 時，同樣的偏心力值作用下構(gòu)件的應(yīng)力應(yīng)變曲線已達(dá)到了強度極限值，由荷載位移曲線與應(yīng)力應(yīng)變曲線可得，構(gòu)件的彈性極值約為635.748kN，此時對應(yīng)的軸壓比n2=0.5127。

3 波紋腹板幾何參數(shù)對構(gòu)件軸壓比的影響規(guī)律

利用控制變量法，對照表2 分別改變構(gòu)件的波折角度、波長、波高、翼緣寬厚比、腹板厚度來觀察構(gòu)件軸壓比的變化規(guī)律。

3.1 波折角度的影響

基于表2，保持其他參數(shù)不變，通過改變構(gòu)件的波折角度來觀察軸壓比的變化情況，角度取值分別為22.64°、30°、45°、60°、75°、90°。

表5 波折角度對軸壓比的影響

3.2 波長的影響

基于表1，保持其他參數(shù)不變，通過改變構(gòu)件的波長來觀察構(gòu)件軸壓比的變化情況，波長值分別為150mm、180mm、210mm、240mm、270mm、300mm。

3.3 波高的影響

基于表2，保持其他參數(shù)不變，通過改變構(gòu)件的波高來觀察構(gòu)件軸壓比的變化情況，構(gòu)件波高值分別為10mm、20mm、30mm、40mm、50mm、60mm。

表6 波長對軸壓比的影響

表7 波高對軸壓比的影響

3.4 腹板厚度的影響

基于表2，保持其他參數(shù)不變，通過改變構(gòu)件的腹板厚度來觀察構(gòu)件的軸壓比變化情況，構(gòu)件腹板厚度值分別為2mm、3mm、4mm、5mm。

表8 腹板厚度對軸壓比的影響

3.5 翼緣尺寸的影響

基于表2，保持其他參數(shù)不變，通過改變構(gòu)件的翼寬比來觀察構(gòu)件的軸壓比變化情況，翼緣厚寬比分別為0.025、0.05、0.075、0.1。

表9 翼緣寬厚比對軸壓比的影響

4 結(jié)論

（1）波紋腹板H 型鋼構(gòu)件波長的變化僅會影響構(gòu)件在偏心荷載作用下的強度極限值，波長太大時會使構(gòu)件的延性變差；

（2）構(gòu)件的延性隨波高的增加而增加；

（3）波紋腹板H 型鋼構(gòu)件的腹板厚度對軸壓的影響較小；

（4）翼緣尺寸對構(gòu)件的軸壓比值的影響較大；

（5）若將構(gòu)件控制在彈性階段則軸壓比值可以0.51 為限值，但若以強度破壞作為構(gòu)件破壞的控制標(biāo)準(zhǔn)，則軸壓比的值要視構(gòu)件的各項幾何參數(shù)綜合而定。