“田”格等比定理

陸敬山

(上海市崇明中學 202150)

“田”字格是一種常見圖形，它普遍存在于凸四邊形之中.例如凸四邊形ABCD中，點P1,P2分別為對邊AB,CD上的點，點Q1,Q2為另一組對邊BC,AD上的點，P1P2與Q1Q2交于點O,(如圖1)，田字格就是指這類圖形，圖中包含了三對橫向線段AQ2，Q2D，P1O，OP2，BQ1，Q1C，三對縱向線段AP1，P1B，DP2，P2C，Q2O，OQ1，本文所說的“田”格等比定理就是以這幾對線段成等比關系作為條件或作為結論的定理，如未特別說明，文中的四邊形是指平面上的凸四邊形.

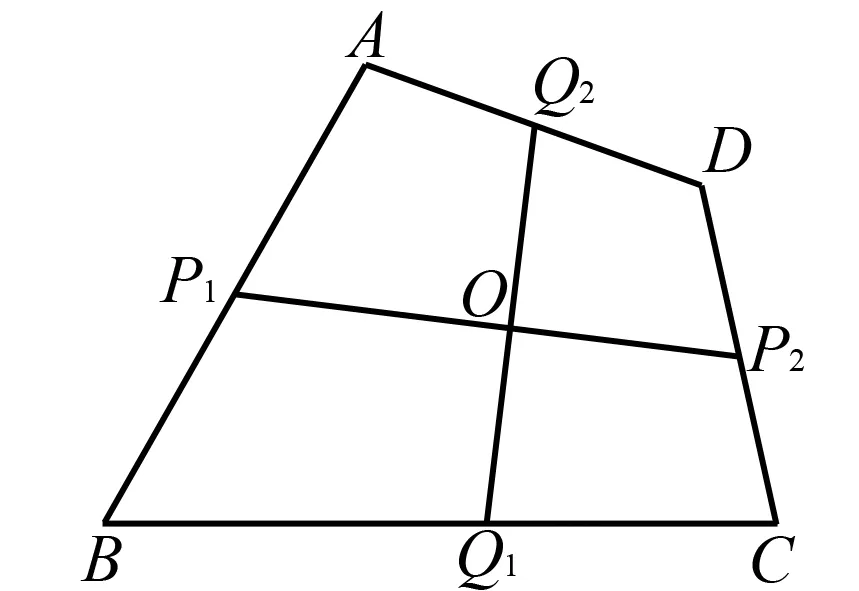
圖1

1 接受啟發，雛形初現

如圖2所示，有一條公共邊的兩個三角形拼接到一起，兩條截線相交，且交點落在公共邊所在直線上，線段之間會有怎樣的比例關系，實際上問題來到了四邊形中，進而又想到了圖1中的“田”字格.

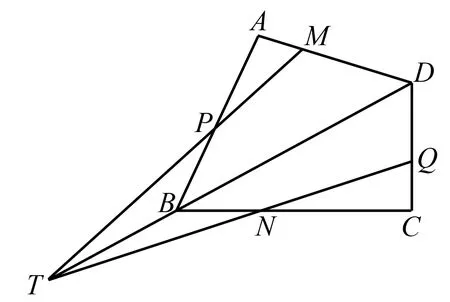
圖2

受到梅涅勞斯定理的啟發，發現下面的問題：

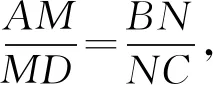
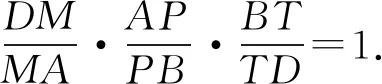
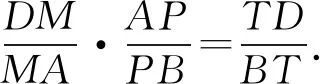
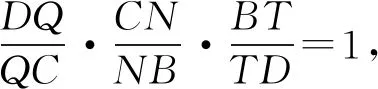
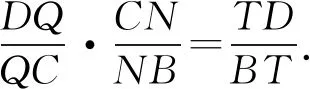
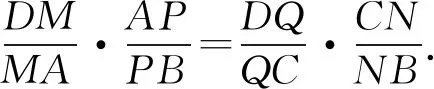
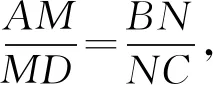
本問題中是MP與QN交于一點T，且點T落在DB的延長線上，如果是MN與PQ交于四邊形內部一點O(如圖3)，添加什么樣的比例關系？又能得出怎樣的結論？

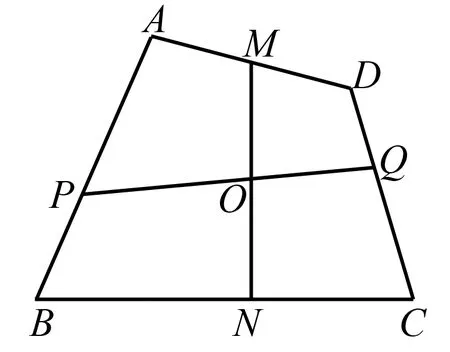
圖3

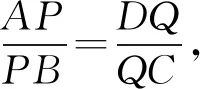
(1)直線MP,NQ,BD三線互相平行或交于一點.

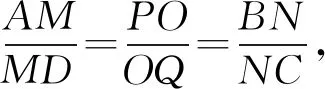
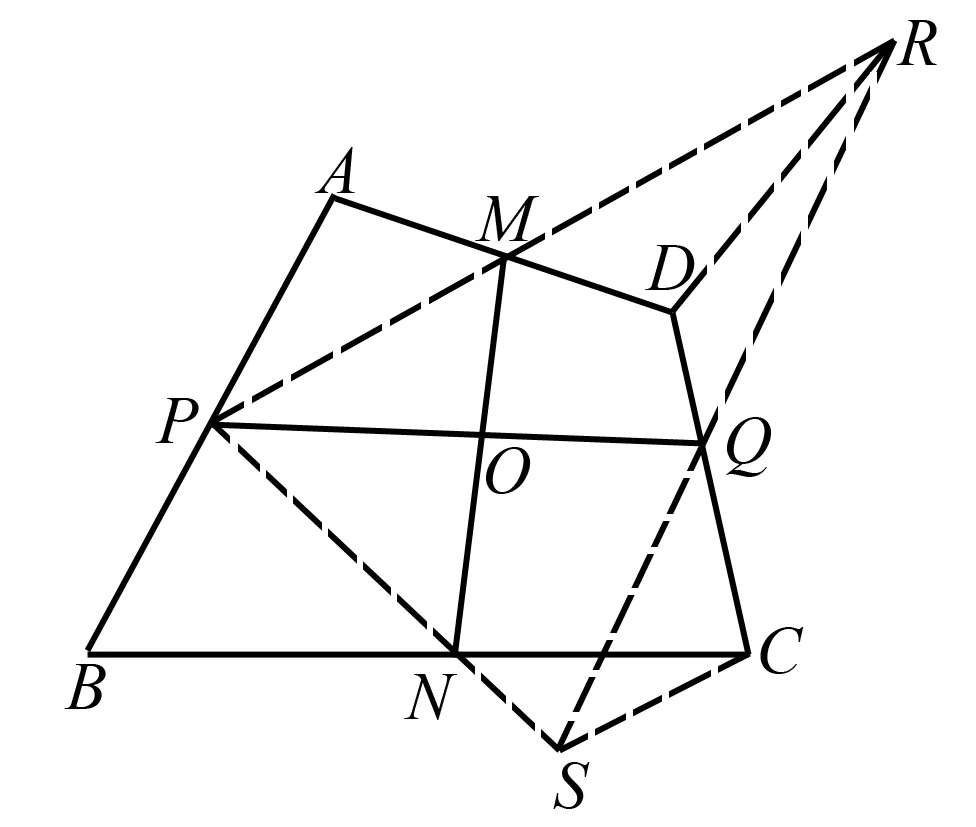
圖4

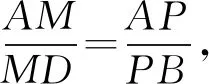
所以MP∥BD,NQ∥BD.

從而MP∥NQ∥BD.

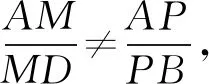
所以MP不平行于BD,NQ不平行于BD.

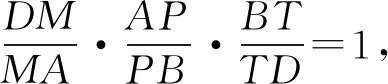
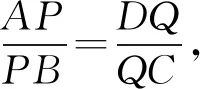
因為T,T′都為線段DB的外分點，從而T,T′重合，即PM,BD,CN三線共點.

故直線MP,NQ,BD三線互相平行或交于一點.

(2)如果ABCD為平行四邊形，則結論(2)顯然成立.

如果ABCD不是平行四邊形，可假設AB不平行于CD,如圖4，過點D作AB的平行線交PM的延長線于點R，再過點C作AB的平行線交PN的延長線于點S，連接RQ及SQ，在△DRQ及△CSQ中，DR∥AB,CS∥AB.

所以DR∥CS，∠RDQ=∠SCQ.

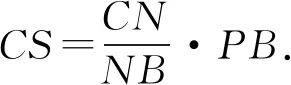
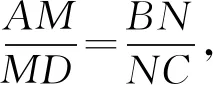
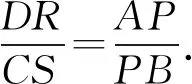
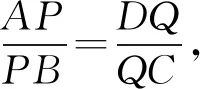
從而△DRQ∽△CSQ.即∠DQR=∠CQS.

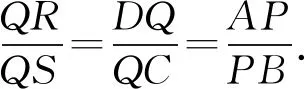
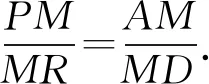
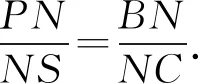
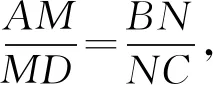
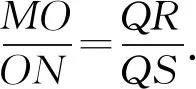
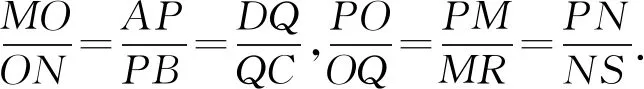
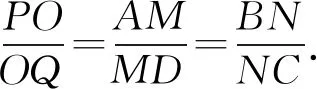
所以結論2成立.本文將問題2稱為田格等比定理的預備定理.

2 千呼萬喚始出來

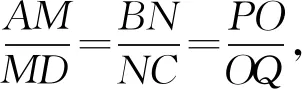
證明如圖4，過點D作AB的平行線交PM的延長線于點R，再過點C作AB的平行線交PN的延長線于點S，連接RQ及SQ，則可得△APM∽△DRM,△BPN∽△CSN.

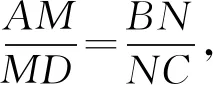
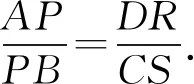
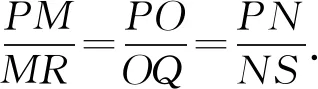
所以RQ∥MO,QS∥ON.

所以R，Q，S三點共線.

所以RS∥MN.

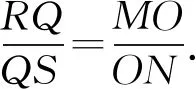
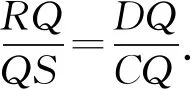
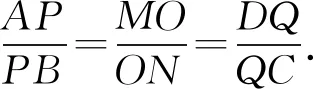
注本人將問題3稱為田格等比定理，其中AB不平行于CD是必要的，如果AB∥CD，則R，D，Q三點共線，S，C，Q也三點共線，△QPD及△QSC不存在，定理不成立.

3 理定而后可道

首先定義等分網格圖：在四邊形ABCD中，點列P1，P2，P3，…，Pn-1.順次將ABn等分，點列Q1，Q2，Q3，…，Qn-1順次將DCn等分，M1，M2，M3，…，Mm-1順次將ADm等分，N1，N2，N3，…，Nm-1順次將邊BCm等分，則連線PiQi及MjNj(i=1，2，3，…，n-1,j=1，2，3，…，m-1)連同四邊形ABCD組成的圖形稱為四邊形ABCD的等分網格圖(如圖5).由田格等比定理可得出下面推論：

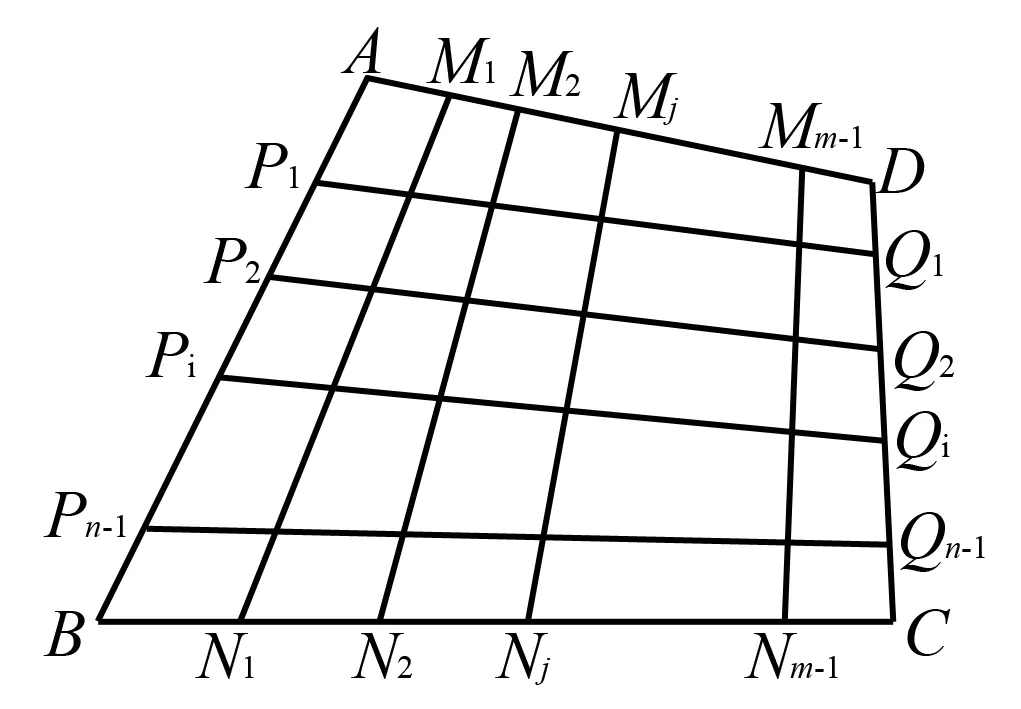
圖5

在平面n×m等分網格圖ABCD中，設PiQi與MjNj(i=1，2，3，…，n-1,j=1，2，3，…，m-1)的交點為Oij,則Oij為PiQi的第j個m等分點，且為MjNj的第i個等分點.

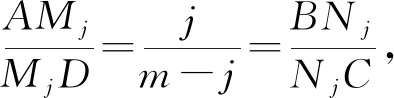
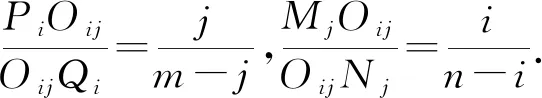
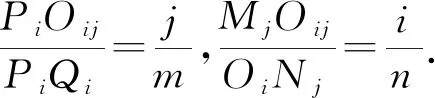
所以推論的結論成立.

4 打鐵還需自身硬

師者，所以傳道授業解惑也.作為一名中學數學教師，要提升學生的數學核心素養，自身必須扎實過硬和技高一籌，而定理的發現一般是經歷嚴密的邏輯推理過程，甚至是曲折且漫長，但長期的堅持不懈定能助長學生的推理習慣，本文就是將田格等比定理的生成過程詳盡闡述并展現.大家知道邏輯推理能力的提升更是核心素養培育的任務之一，希望更多師者投身到研究中來，努力提升自身的核心素養.