動量碰撞問題不都是口算嗎？

熊高云

(江西省南康中學北校區 341400)

對于完全彈性碰撞和完全非彈性碰撞其實都有一個共同的時刻即碰撞的兩物體形變最大，也是兩物體的速度相等的時刻，只不過是完全非彈性碰撞的兩物體以此速度結束碰撞過程，而完全彈性碰撞則是兩物體的形變又恢復到原狀，解決此類問題需要抓住此狀態.碰撞問題中大到分為動碰靜和動碰動，前者處理較為簡單，在此不作分析，主要分析動碰動的情形.

例如：如圖1，在光滑的水平面上，質量為m1的小球A以速度v1向右運動，質量為m2的小球B以v2也向右運動，且v1>v2，小球A追上小球B發生完全彈性碰撞，試求兩小球碰撞后的速度分別為多少？

圖1

1 常規方法

碰撞過程中由動量守恒得

由能量守恒得

聯立解得

對于此結果，雖然是通過兩個過程聯立解得，但是解答過程還是很復雜，在考試過程中由于時間有限不可能有時間讓你去解.有的老師，可能也會要求學生把這個結論記下來，到時直接用，但大家發現，兩個速度公式也很麻煩，一但記憶出現一點小問題，最后的結果就都是錯誤的，所以，對于這類問題是不光是學生的難點，也是老師的難點，反正筆者從教16年，現在還沒有完全記下兩個速度.

2 方法升級理解

由常規方法得到的兩小球碰后的速度為

對兩速度公式進行變形如下

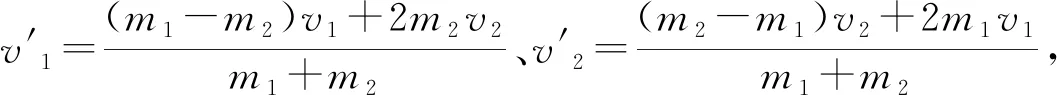
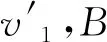
3 實戰應用

題1(2022·江蘇·模擬預測)質量相等的A、B兩球在光滑水平面上沿同一直線、同一方向運動，A球的速度vA=5m/s，B球的速度vB=3m/s，當A球追上B球時發生碰撞，則碰撞后A、B兩球速度可能為( ).

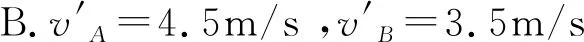
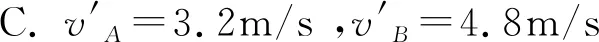
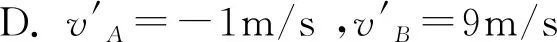
常規解法兩球組成的系統動量守恒，以兩球的初速度方向為正方向，如果兩球發生完全非彈性碰撞，由動量守恒定律得

mvA+mvB=2mv

帶入數據解得

v=4m/s

如果兩球發生完全彈性碰撞，由動量守恒定律得

由機械能守恒定律得

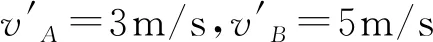
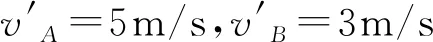
故兩球碰撞后的速度范圍是

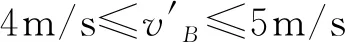
ABD不符合題意，C符合題意.

故選C.

速度增量法：先由動量守恒定律得

mvA+mvB=2mv共

帶入數據解得

v共=4m/s

由速度增量法可知

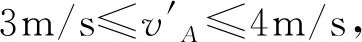
題2(2020·吉林吉林·二模)兩球A、B在光滑水平面上沿同一直線、同一方向運動，mA=1 kg，mB=2 kg，vA=6 m/s，vB=2 m/s.當A追上B并發生碰撞后，兩球A、B速度的可能值是( ).

A.vA′=3 m/s，vB′=4 m/s

B.vA′=5 m/s，vB′=2.5 m/s

C.vA′=2 m/s，vB′=4 m/s

D.vA′=-4 m/s，vB′=7 m/s

常規方法(略)

速度增量法：

碰撞過程中的共同速度為

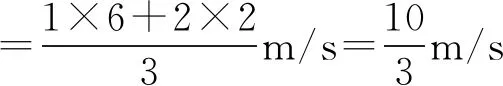
則碰撞后A、B球的速度

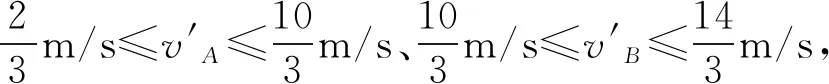
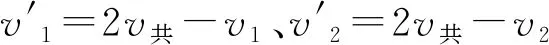
題3(2019·江西·鷹潭一中高三階段練習)在光滑水平面上，兩球沿同一條直線同向運動，質量為2kg的A小球速度為2m/s，質量為1kg的B小球速度為1m/s，兩球發生彈性碰撞，求碰后兩球速度大小.

圖2

常規方法對于兩球組成的系統，水平方向不受外力，動量守恒.由動量守恒可得：

mAv1+mBv2=mAvA+mAvB

由彈性碰撞知機械能守恒，得：

聯立方程代入數據得：

此方法看上去只有兩個方程，但要真正計算到結果還是有點難度的，特別當兩物體的速度不是整數時，速度平方那更是難計算了.

速度增量法

很明顯用速度增量法減小了平方的項的計算，使計算又快又準.