借助極限思維法 巧解高中物理題

王宗波

(山東省日照第一中學(xué) 276800)

極限思維法主要是兩個(gè)量在某個(gè)空間中的變化關(guān)系，如單調(diào)上升或者下降的函數(shù)關(guān)系，通過改變其中的量，使得空間內(nèi)變化在某個(gè)區(qū)間內(nèi)達(dá)到極限.在高中物理解題中，極限思維法有著重要的作用，借助極限思維法有利于高中物理教學(xué)發(fā)展，提高學(xué)生解題能力，因此，需要不斷優(yōu)化極限思維法，加強(qiáng)極限思維法的應(yīng)用.借助極限思維法解決綜合性強(qiáng)和復(fù)雜性問題，提高學(xué)生物理解題效率.

1 高中物理解題中極限思維法應(yīng)用的重要性

高中物理解題中，極限思維法有著重要的作用，借助有效的思維方式和解題方法，將事物變化限定在極端內(nèi)，在任意的空間或者事物中都可以進(jìn)行設(shè)置，對(duì)事物變化過程中發(fā)展規(guī)律進(jìn)行分析，找出問題解決的有效方式.極限思維法在高中解題中應(yīng)用，能夠?qū)?fù)雜問題簡單化，使得物理解題思路更加清晰，在解題過程中，能夠從極端思路出發(fā)，深入理解題目信息，了解解題方式，簡化解題步驟.總體來說，極限思維法能夠提高學(xué)生學(xué)習(xí)成績，幫助學(xué)生掌握解題方法，得到高中學(xué)生的認(rèn)可，實(shí)現(xiàn)學(xué)生的全面發(fā)展.

2 高中物理解題中極限思維法的應(yīng)用

2.1 借助極限思維法，明確解題突破點(diǎn)

高中物理知識(shí)具有復(fù)雜性的特點(diǎn)，體現(xiàn)在各種類型題目中，對(duì)于條件多、數(shù)據(jù)復(fù)雜的題目類型，解題信息獲取難度較大，面對(duì)這樣的情況，借助極限思維法，能夠提高解題效果.高中物理解題中，借助極限思維，假設(shè)任意變量，在空間內(nèi)達(dá)到極限點(diǎn)，完成題目解答.通過這樣的方式，幫助學(xué)生找出解題思路，剔除無用無關(guān)信息，提高學(xué)生解題效率.

例題如圖1所示，在一口深井中提出一個(gè)物體，現(xiàn)在采取定滑輪提取的方式，使用汽車和定滑輪組合，在滑輪上的繩子是PQ，物體的質(zhì)量是m，在汽車后面掛鉤位置掛上繩子P端，繩子的Q端和物體相連.假設(shè)繩子總長度不變化，忽略繩子、定滑輪的質(zhì)量，滑輪上的摩擦力不計(jì)，當(dāng)汽車開始運(yùn)動(dòng)時(shí)，汽車位于A點(diǎn)，繩子處于繃直狀態(tài)，兩側(cè)繩子都處于豎直方向，定滑輪左側(cè)繩子長度是H，當(dāng)物體提升時(shí)，汽車向左做加速運(yùn)動(dòng)，沿著水平方向從A點(diǎn)運(yùn)動(dòng)到C點(diǎn)，途中經(jīng)過B點(diǎn).如果A點(diǎn)到B點(diǎn)的距離也是H，經(jīng)過B時(shí)，汽車的速度是VB，求解汽車從A點(diǎn)到B點(diǎn)的運(yùn)動(dòng)中，繩子對(duì)物體所做的功.

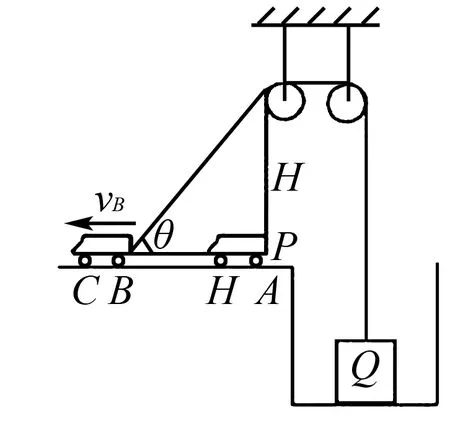
圖1

解析對(duì)于此種類型題目，題目中并沒有給出到達(dá)B點(diǎn)時(shí)物體的速度，使得解題較為困難.在解題中，學(xué)生很容易出現(xiàn)錯(cuò)誤，如將汽車到達(dá)B點(diǎn)時(shí)的速度和物體速度等同，對(duì)于這樣的錯(cuò)誤，主要是學(xué)生沒有考慮速度方向.想要解答此題目，需要明確兩者速度的關(guān)系，結(jié)合圖1可以得出，繩子的速度和θ角的變化有關(guān)，θ角則隨著汽車從A到B再到C的過程發(fā)生變化.作為教師，需要引導(dǎo)學(xué)生利用極限思維法，利用兩個(gè)理想極限值完成解題.當(dāng)汽車在A點(diǎn)時(shí)，θ=90°，繩子的速度是0，當(dāng)汽車行駛到無窮遠(yuǎn)時(shí)，θ=0°，繩子的速度和汽車速度相同.因此，汽車A點(diǎn)到無窮遠(yuǎn)的區(qū)間內(nèi)，繩子速度的變化規(guī)律是V=V車cos90°=V車，通過這樣得出汽車到B點(diǎn)的速度，V=VBcosθ，計(jì)算出汽車到達(dá)B點(diǎn)時(shí)物體的速度.通過極限思維法，明確解題思路，突破解題難點(diǎn)，輕松求解出繩子對(duì)物體做的功.

2.2 借助極限思維法，明確解題思路

高中物理解題中，除了找出解題突破點(diǎn)，還需要有著明確的解題思路，根據(jù)解題將需要的知識(shí)點(diǎn)聯(lián)系在一起，得到最佳的解題方式.根據(jù)這樣的解題需求，教師可以引導(dǎo)學(xué)生利用極限思維，將題目問題進(jìn)行極限轉(zhuǎn)化，有效完成問題解答.

例題如圖2所示，在水平面上放置有甲、乙兩個(gè)斜坡裝置，斜坡的坡面是光滑的，兩個(gè)斜坡的高度相同，從頂端到底端的距離是一樣的，斜面甲是直線，斜面乙則分為兩個(gè)部分，如果在兩個(gè)斜面頂端分別靜止釋放一個(gè)小球，只考慮重力做的功，請(qǐng)問小球在那個(gè)斜面最先到達(dá)底端？(兩個(gè)小球完全相同)

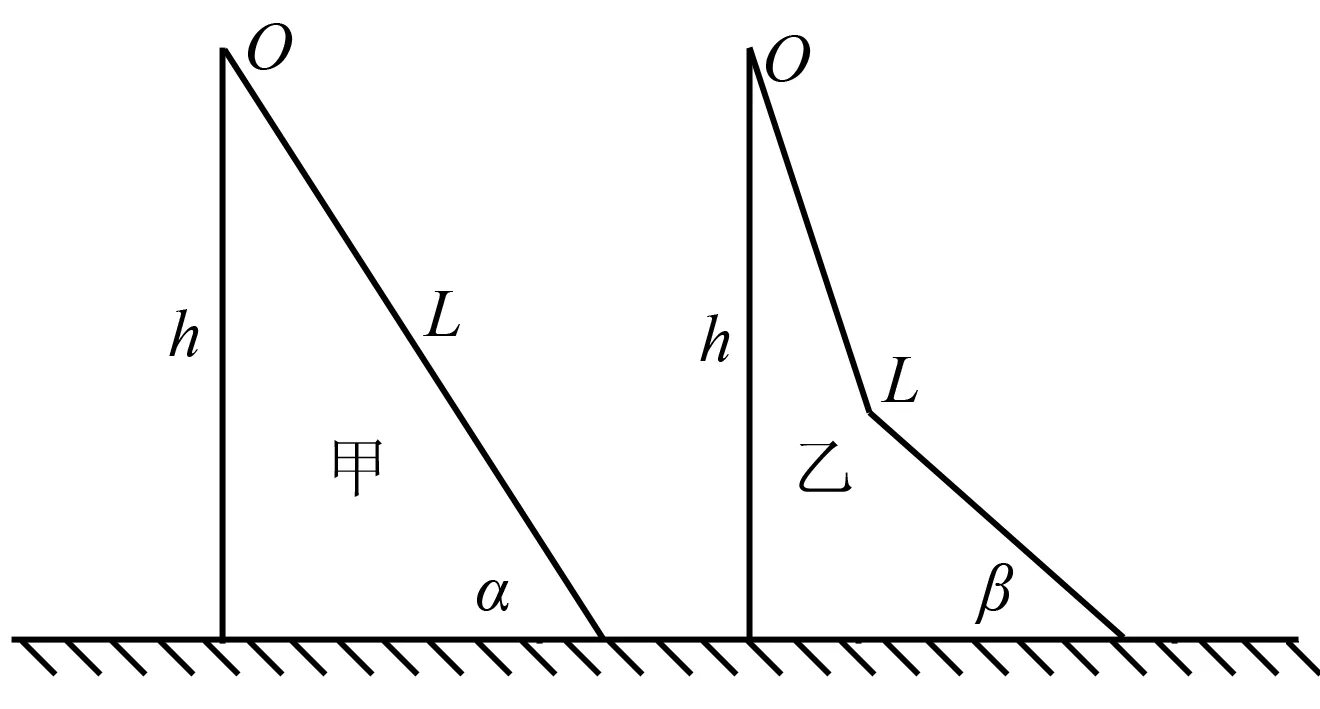
圖2

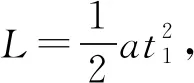
2.3 利用極限思維法，提高學(xué)生解題效率

在高中物理解題中，大部分的物理題目求解時(shí)，對(duì)物理變量有著一定的區(qū)間限定，針對(duì)此種類型的問題，教師可以讓學(xué)生利用極限思維方式，對(duì)臨界值進(jìn)行推算或者假設(shè)，在對(duì)臨界狀態(tài)做出分析之后，形成問題分析和解答的基準(zhǔn)，有效提高學(xué)生解題效率.

例題如圖3所示，圖中的裝置處于平衡狀態(tài)，將AC換成長一些的繩子AC′，桿AB處于豎直狀態(tài)，裝置依舊處于平衡狀態(tài)，那么繩子AC'受到的張力FT和桿AB受到的壓力FN相對(duì)于原來來說，有什么樣的變化( ).

A.FT增加，F(xiàn)N減少 B.FT、FN都增加

C.FT減少，F(xiàn)N增加 D.FT、FN都減少

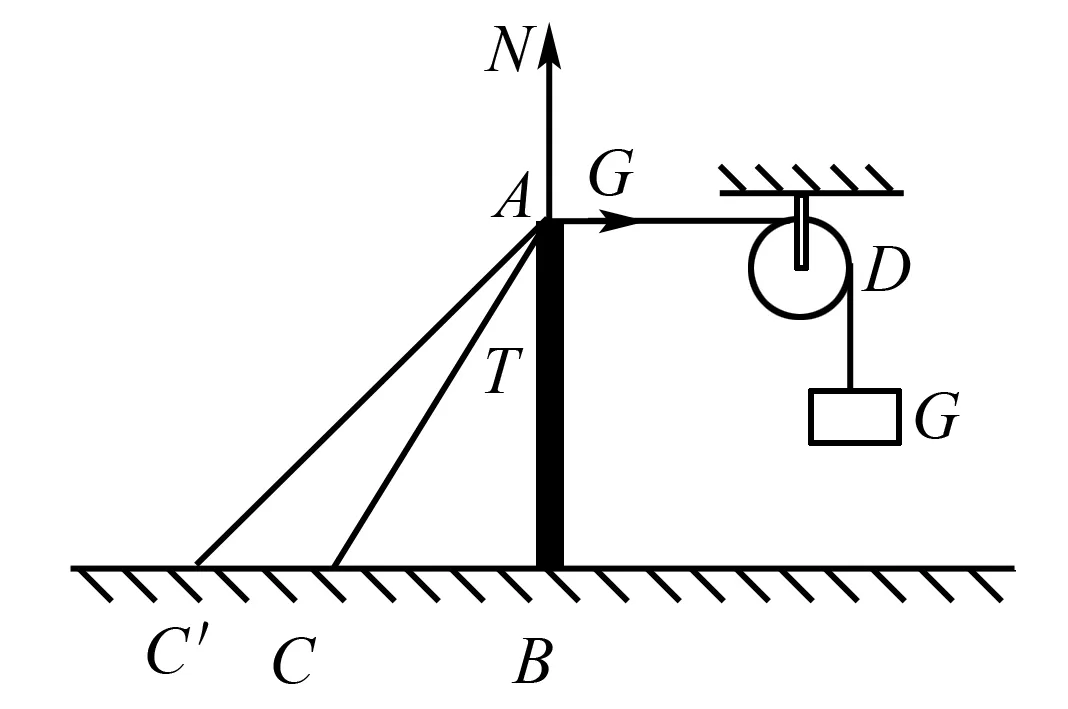
圖3

解析教師可以引導(dǎo)學(xué)生利用極限思維法，幫助學(xué)生找出解題思路.根據(jù)題目假設(shè)繩索AC和水平面的夾角是0°，即繩索和AB垂直，此時(shí)的FT=G，F(xiàn)N=0，之后，假設(shè)繩索AC和水平面的夾角是90°，此時(shí)FT=FN，且FT趨向無限大.根據(jù)結(jié)論對(duì)題目進(jìn)行分析，在繩索更換成AC′后，其和水平面的夾角逐漸變小，在夾角從90°到0°的變化中，F(xiàn)T值和FN值在逐漸變小，得出相應(yīng)的結(jié)論，簡化解題過程，明確問題解題方式.對(duì)圖進(jìn)行分析，得出當(dāng)θ為零時(shí)，F(xiàn)T=G，F(xiàn)N=0，當(dāng)θ=90°時(shí)，F(xiàn)N很大，F(xiàn)T隨著FN的增加而增加，當(dāng)θ減小時(shí)，F(xiàn)T和FN也逐漸減小.

2.4 借助極限思維法，培養(yǎng)學(xué)生靈活思維

高中物理解題中，利用極限思維法解決計(jì)算和分析題目外，還可以讓學(xué)生利用極限思維法解決選擇，引導(dǎo)學(xué)生采取靈活的方式解題，保證解題效率和準(zhǔn)確性，讓學(xué)生可以更快的找出答案.

例題一輛小車上有著一個(gè)固定的斜面，使用細(xì)繩將一個(gè)小球連在車頂，此時(shí)小車在水平面做直線運(yùn)動(dòng)，如果某個(gè)時(shí)刻，小球處于如圖4中的狀態(tài)，斜面對(duì)小球的支撐力是FN，細(xì)繩拉力是FT，下述有關(guān)小球此時(shí)受力分析正確的是( ).

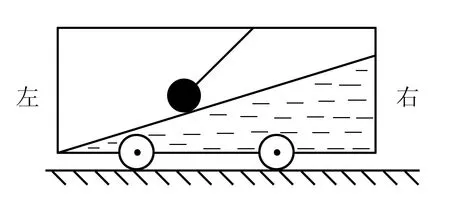
圖4

A.小車向左運(yùn)動(dòng)時(shí)，F(xiàn)N的值可能是0

B.小車向左運(yùn)動(dòng)時(shí)，F(xiàn)T的值可能是0

B.小車向右運(yùn)動(dòng)時(shí)，F(xiàn)N的值不可能是0

D小車向右運(yùn)動(dòng)時(shí)，F(xiàn)T的值不可能是0

解析根據(jù)選項(xiàng)中的結(jié)論，可以讓學(xué)生利用極限思維的方式思考問題，在分析FN時(shí)，假設(shè)斜面對(duì)小球的支持力FN是0，小球則只受到重力和拉力作用，并且其合力是水平向右，此時(shí)小車有可能是向右做加速運(yùn)動(dòng)，或者是向左做減速運(yùn)動(dòng)，因此，可以得出選擇A正確，選項(xiàng)C錯(cuò)誤.在分析FT時(shí)，假設(shè)繩索拉力FT是0，小球受到重力和支持力，合力水平向左，小車可能向左加速運(yùn)動(dòng)，也可能是向右減速運(yùn)動(dòng)，因此，B選項(xiàng)正確，D選項(xiàng)錯(cuò)誤.

2.5 利用極限思維法，快速解答疑難問題

運(yùn)動(dòng)學(xué)是高中物理的重要內(nèi)容，主要有勻加速直線運(yùn)動(dòng)、平拋運(yùn)動(dòng)、圓周運(yùn)動(dòng)等，豎直上拋運(yùn)動(dòng)則是勻加速直線運(yùn)動(dòng)的重要內(nèi)容，物體上升時(shí)，受到重力和空氣阻力影響，兩者方向豎直向下，下落時(shí)，物體重力方向向下，空氣阻力向上.高中物理習(xí)題中，結(jié)合豎直上拋內(nèi)容，考查學(xué)生對(duì)勻加速直線運(yùn)動(dòng)的理解，要求學(xué)生具備靈活的思維，針對(duì)問題做出分析，利用極限思維法，提高解題效率.

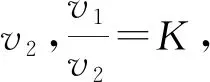
解析假設(shè)空氣阻力無限趨向于零，那么f和重力G的比值則無限接近零，此時(shí)K的值則趨向接近于1，此題是選擇題，可以將K=1帶入其中，選擇中結(jié)果為零的則是正確選項(xiàng)，正確答案是D.

2.6 利用極限思維法，掌握解題技巧

彈簧類習(xí)題是高中物理的常見題型，能夠考查學(xué)生對(duì)受力知識(shí)以及能量知識(shí)的掌握程度.彈簧形變不同，則是會(huì)產(chǎn)生不同的力的效果，學(xué)生對(duì)問題分析時(shí)，難以做好準(zhǔn)確把握.為了幫助學(xué)生掌握解題技巧，注重直觀方式展示不同形態(tài)下彈簧彈力的情況，夯實(shí)學(xué)生基礎(chǔ)知識(shí)，借助極限思維法的利用，鍛煉學(xué)生思維能力，面對(duì)類似的問題，能夠采取多種解題方式，靈活利用解題技巧，保證答案的準(zhǔn)確性.

例題如圖5所示，一個(gè)輕質(zhì)彈簧的兩端各連接一個(gè)小球，小球質(zhì)量分別是m1、m2，使用一根細(xì)線L1將m1和OO'軸相連.如果兩個(gè)小球均以角速度ω在光滑水平面轉(zhuǎn)動(dòng)，兩球之間距離是L2.在某一時(shí)刻細(xì)線忽然斷開，在斷開的一瞬，兩個(gè)球的加速度分別是( ).

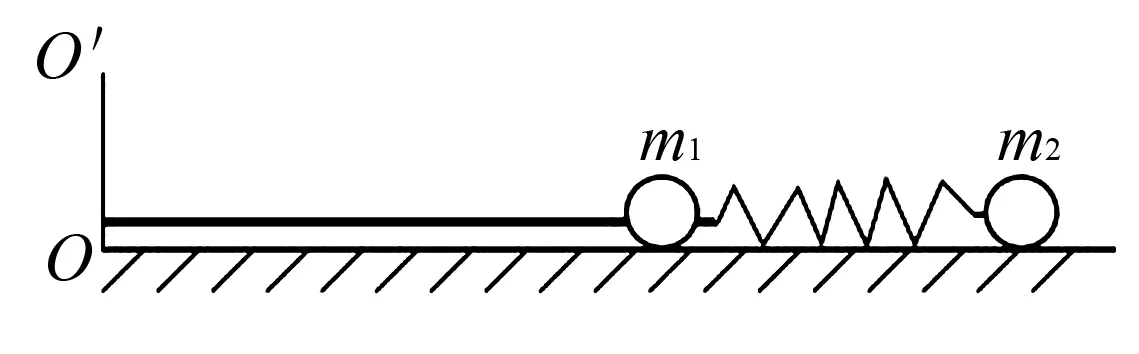
圖5

A.a1=ω2L1,a2=ω2(L2+L1)，兩者方向一致

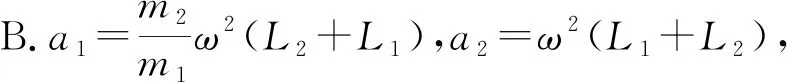
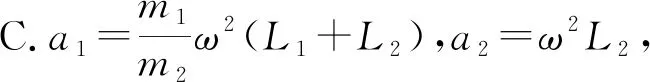
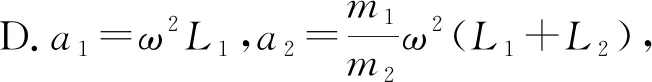
解析得出正確的答案.根據(jù)兩個(gè)小球的質(zhì)量m1和m2，假設(shè)m1無限接近m2，在細(xì)繩斷開時(shí)，彈簧受力大小一致，方向相反，那么兩個(gè)小球的加速度也是一致的，方向也是相反的.將m1=m2帶入四個(gè)選項(xiàng)，找出B選項(xiàng)符合要求.

2.7 利用極限思維法，檢驗(yàn)問題結(jié)果

高中物理解題中，利用極限思維檢驗(yàn)計(jì)算結(jié)果，能夠判斷結(jié)果的準(zhǔn)確性，提高學(xué)生解題準(zhǔn)確率，有利于學(xué)生考試成績的提升.

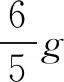
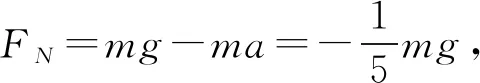
在高中物理解題中，利用極限思維法，能夠達(dá)到事半功倍的效果，借助極限思維法，幫助學(xué)生理解分析問題，尋找解題突破點(diǎn)，明確解題思路，掌握解題方法和技巧，提高學(xué)生解題效率.同時(shí)，利用極限思維法，能夠檢驗(yàn)物理解題結(jié)果，培養(yǎng)學(xué)生嚴(yán)謹(jǐn)?shù)膶W(xué)習(xí)態(tài)度，實(shí)現(xiàn)復(fù)雜問題簡單化，提高學(xué)生解題效率和質(zhì)量.