河道清淤工程淤積方量計算方法的對比研究與應用

廖 月 侯 煜 張勁軍 張楚楚 楊艷慧

（江蘇省泰州引江河管理處 泰州 225321）

1 引言

淤積方量的計算是目前河道清淤施工中最為重要的工作之一，不僅在前期對工程預算和施工方案的選擇有重要的指導意義，還是施工結束工作量復核的重要依據。對于不同地形地貌，選擇計算方法是不一樣的，目前常用的淤積方量計算方法主要有斷面法、DTM法、方格網法及等高線法四種。本文采用基于AutoCAD平臺的南方CASS軟件，探究四種計算方法原理及優劣，結合高港樞紐下游引水河道清淤工程實例，分析四種計算方法在實際應用中的精確度。

2 河道淤積方量計算方法的原理

2.1 斷面法

斷面法多應用于河道、溝渠、管道等狹長的條狀地形，同時也適用于面狀及有臺有坎地形。在地形圖或碎部測量的平面圖上，以固定的間距等分土方的計算范圍，將其劃分成數個相互平行的橫斷面，按照現有斷面線及設計斷面線組成的斷面圖計算挖填面積，兩個相鄰橫斷面的平均面積與斷面間距的乘積即為兩斷面間的挖填方量，將各段區域的值累加即可得到整個區域的挖填方量。

設橫斷面面積分別是S1，S2，S3……Sn；斷面間距為H，則總的挖填方量為：

2.2 DTM法

數字地面模型（DigitalTerrainModel，DTM）是地貌形態的離散表示，用坐標（X,Y,Z）表達區域內的地貌形態。DTM法適用于計算復雜地貌至水平平面的挖填方量，根據實測地面點坐標（X,Y,Z）和設計高程，利用復合線劃定挖填分界線，生成不規則三角網計算每個三棱錐的挖填方量，最后累加得到整個區域的挖填方量。另外也可對同一區域進行兩期測量，通過兩次測量得到的高程數據進行建模，計算出兩期整個區域的土方變化，即可得到整個區域完成的土方挖填量。

設E、F、G為三角網的三個頂點，它們到設計高程的高差分別是h1、h2和h3；S為三棱錐的底面積，則總的挖填方量為：

2.3 方格網法

方格網法與DTM法前期工作基本一致，但適用于地形變化較小的區域。根據實測地面點坐標（X,Y,Z）和設計高程，先將待計算的區域生成若干個方格，再將方格的四個角上的高程相加，取平均值與設計高程相減，然后根據方格邊長利用長方體體積計算公式得到每個方格的挖填方量，最后累計得到整個區域的挖填方量。

設方格網邊長為a、b；hij表示第i行j列的方格網高差；n為測區方格的個數。總的挖填方量為：

2.4 等高線法

等高線法適用于等高線完全閉合區域，利用兩條等高線圍成的面積和高差來計算兩條等高線之間的土方量。兩條等高線之間的體積可以近似看作截錐體，先計算出兩條等高線圍成的面積，再利用兩條等高線之間的高差，通過計算公式可以算出兩條等高線所圍的土方量。

設Sn、Sn-1為任意兩條等高線的截椎體底面積；hn、hn-1為任意兩條等高線的高程，則任意兩條等高線的挖填方量為：

3 河道淤積方量計算方法的優劣對比

3.1 斷面法

用斷面法計算清淤方量，斷面線的布置十分關鍵，必須遵循以下布設原則：①在平順且河床地形變化不大的河道，河道斷面可以平均布設，垂直于河道主流方向，距離可以適當調遠；②當河道彎曲或河床地形變化較大的區域，應加密設置河道斷面線，滿足計算淤積量的精度要求；③在河道主流方向變化較大的區域，同樣應加密布置河道斷面線，使劃分的各個區域斷面線垂直于主流方向，以便于確定斷面間距，確保計算清淤方量的準確度。

用斷面法計算清淤方量，當斷面布置較近時，雖然計算精度有保障，但外業測量及內業計算量較大；當斷面布置較遠時，雖然外業及內業工作相對減少，但精度較差。同時斷面法必須對各斷面的參數包括設計坡比、河底高程的設置比較清楚，鑒于斷面法受到的諸多限制，在河道彎曲及河床地形變化較大時，計算精度和可靠性很難獲得保證。

3.2 DTM法

DTM法從理論上講能夠適應各種地形地貌，通過測深儀采集河床特征點高程，所形成的三角網能直觀地展現地形特征，同時可以將使用的高程點作為水下地形圖高程點而無須重新測量，具有較高的計算精度。但DTM法在建模時通常比較復雜，需要軟件進行輔助測量，同時需要大量的數據來確保建模的準確性，這就要求在使用DTM法時要盡可能采集更多的高程點，高程點的精度、密度和均勻性與計算結果息息相關。

3.3 方格網法

方格網法相對簡明直觀、通用性強，可以生成挖填線，但由于方格網法需要提取4個角上的高程來計算方格網的體積，有時角上沒有高程點，需要利用其他高程點內插得到該處的高程點，同時圖上等高線與實際地形有很大的差距，計算出的清淤方量必然也有很大的差距。只有地形越平緩，各個方格點的圖上高程與實際高程越接近，計算結果才能越精確。

3.4 等高線法

等高線法在計算時精度較低，不但需要地形圖，等高線還必須是閉合的，不適合河道清淤方量的計算，所以等高線法不在本文進行具體討論。但在一些山頭或盆地區域，等高線法是比較合適的方法。

4 河道淤積方量計算方法的工程驗證

4.1 項目概況

高港樞紐是國家南水北調東線規劃的水源工程之一，高港節制閘為中型水閘，由下游（長江側）向上游引水。下游引水河道總長約2.0km左右，平均淤積在2～3m，淤積總方量超過50萬m3。近年來，高港樞紐對下游引水河道進行了3期河道清淤施工，清淤總方量超過16萬m3。

4.2 精度對比

為了驗證3種計算方法的理論精度，本次采用斷面法、DTM法及方格網法分別對河道平順區（C.S.13-C.S.16斷面，河床地形變化較小）及口門區域（C.S.22-C.S.24斷面，河床地形變化較大）進行計算，比對其在不同河道條件下的精確度。

區域土方量平衡是以挖填邊界線為界，計算出一個土方平衡高度，使挖方量等于填方量，可以通過區域土方量平衡法計算的結果來判斷3種計算方法的精確度。根據區域土方量平衡計算，C.S.13-C.S.16斷面平場面積設置為29269.3m2，土方平衡高度-3.096m；C.S.22-C.S.24斷面平場面積設置為26440.6m2，土方平衡高度-2.458m。圖1為區域平衡法圖。

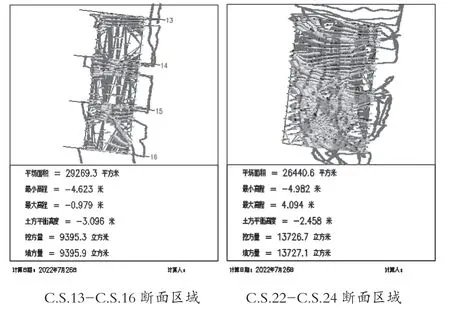
圖1 區域平衡法圖

在平場面積、采樣間隔和平場高度都采取以上數值時，3種計算方法計算結果如表1、表2。

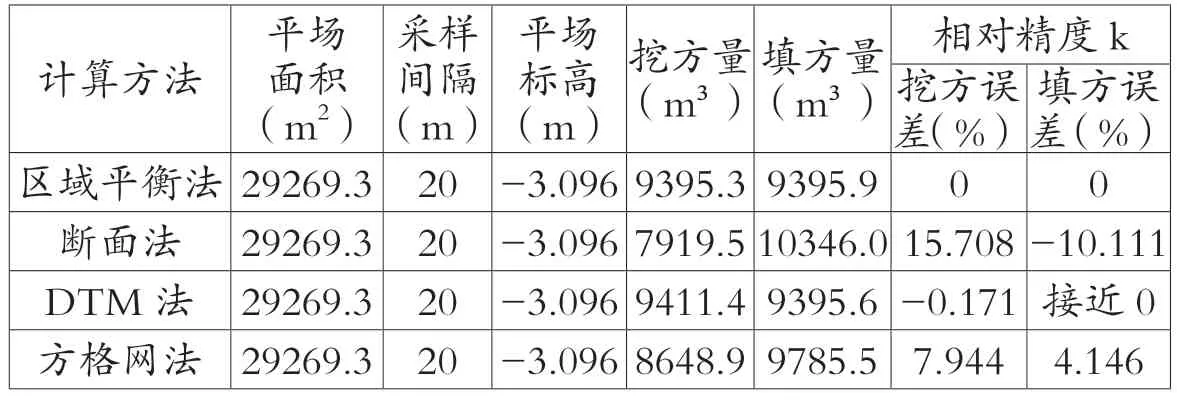
表1 C.S.13-C.S.16斷面相對精度計算表

表2 C.S.22-C.S.24斷面相對精度計算表

通過精度計算表可知，DTM法精度最高，計算結果是可信任的；方格網法次之，無論河道地形有何變化，方格網法的相對誤差均在10%以內；而從結果看，斷面法精度最低，在平順及地形變化不大的河道誤差在10%～15%，而在彎曲及地形變化較大的河道誤差超過了25%。

4.3 清淤方量計算

通過與區域平衡法在兩個區域的比較，發現DTM法在河道清淤方量的計算中精度最高，方格網次之，斷面法精度最低。下面就以C.S.13-C.S.16斷面兩期數據為例，對比三種計算方法得到的數據誤差。

4.3.1 斷面法

應用斷面法計算，該段河道標準斷面的設計高程、坡比均已知，斷面間距為50m。將兩期數據分別生成里程文件，利用二斷面線間土方計算法計算每個斷面清淤前后橫斷面積變化，挖方量為15471.2m3，填方量為3253.3m3。

4.3.2 DTM法

應用DTM法分別對兩期高程數據進行建模，計算出該區域的清淤方量。圖2為DTM法圖。深色部分表示高程發生變化，即此區域已進行了清淤施工。通過軟件計算，得到挖方量為13918.5m3，填方量為1430.7m3。

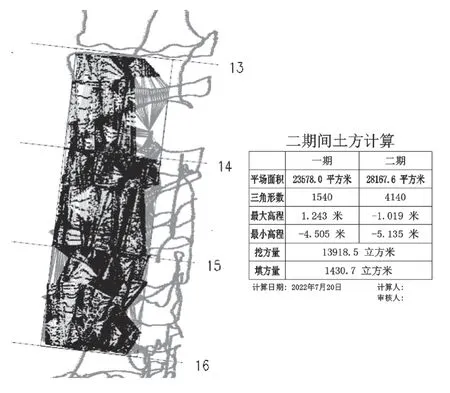
圖2 DTM法圖

4.3.3 方格網法

利用方格網法對相同的區域進行清淤方量計算，方格網法生成的網格以及各個網格自動生成的挖填方量較為利于組織施工。為了計算準確，將兩期河底目標高程均設置為-4m，施工前挖方量為24551.1m3，填方量為500.3m3；施工后挖方量為11990.0m3，填方量為2881.0m3。施工后部分區域存在超挖，方量約為2380.7m3，實際的挖方量為14941.8m3。

4.3.4 計算結果對比

從計算結果顯示，以DTM法13918.5m3為基值，方格網法誤差7.35%，斷面法誤差11.16%。

5 結論

通過以上四種計算方法的對比以及實例研究可以得出：在河道清淤方量的計算中，DTM法在兩期清淤土方的計算中具有無可比擬的精確度及速度優勢，只要在外業中采集到足夠的反應河床變化的高程數據，無論河床地形如何變化，DTM法都可以迅速地計算出清淤方量，不僅提高了工作效率，還可以為清淤工程的準確結算提供有力支撐，因此DTM法可以作為河道清淤方量計算的首選方法■