回首“對(duì)折”，促相等與垂直并行進(jìn)階

金奎

【摘? ?要】“對(duì)折”是軸對(duì)稱學(xué)習(xí)的起始方式，概念進(jìn)階就是對(duì)應(yīng)點(diǎn)的連線被對(duì)稱軸垂直平分。由于學(xué)生受“相等”的定格影響，往往難以發(fā)現(xiàn)“垂直”的關(guān)鍵作用。教學(xué)圍繞“暴露‘一樣到‘重合的認(rèn)知沖突；適配‘折到‘不折的心理跨越；挖掘‘相等并‘垂直的完整內(nèi)涵；重建‘定性到‘定量的原理閉環(huán)”，從而實(shí)現(xiàn)相等與垂直并行進(jìn)階。

【關(guān)鍵詞】對(duì)折；定性；定量；相等；垂直

從圖形的運(yùn)動(dòng)角度看，平移、旋轉(zhuǎn)運(yùn)動(dòng)都是一個(gè)圖形在圖形所在平面上的二維運(yùn)動(dòng)（滑動(dòng)、轉(zhuǎn)動(dòng)）。軸對(duì)稱運(yùn)動(dòng)有別于平移、旋轉(zhuǎn)運(yùn)動(dòng)，它是一個(gè)圖形上的任意一點(diǎn)都以對(duì)稱軸上相應(yīng)的點(diǎn)為圓心，向圖形所在平面外做了180°的圓周運(yùn)動(dòng)。回首“對(duì)折”，軸對(duì)稱運(yùn)動(dòng)的概念需進(jìn)階為對(duì)應(yīng)點(diǎn)的連線被對(duì)稱軸垂直平分。

“對(duì)折”顯見“平分”而難現(xiàn)“垂直”，如何實(shí)現(xiàn)相等與垂直并行進(jìn)階？

一、暴露“一樣”到“重合”的認(rèn)知沖突

二年級(jí)“認(rèn)識(shí)軸對(duì)稱圖形”教學(xué)，旨在讓學(xué)生感知生活中的對(duì)稱現(xiàn)象，通過觀察、剪一剪的操作到感悟“軸對(duì)稱”的數(shù)學(xué)化過程，側(cè)重對(duì)圖形的整體感知。這時(shí)軸對(duì)稱教學(xué)中涉及的運(yùn)動(dòng)常為最直觀的做法：對(duì)折。

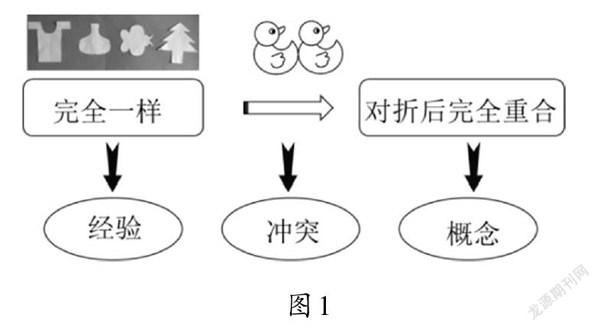
學(xué)生的經(jīng)驗(yàn)來自于“完全一樣”，他們認(rèn)為擁有兩部分完全一樣的圖形即可稱為軸對(duì)稱圖形。此時(shí)的學(xué)生只能給出軸對(duì)稱圖形的主要特征，但無法利用現(xiàn)有的語言體系高度概括出軸對(duì)稱圖形的概念。教師利用一幅呈現(xiàn)同一朝向的兩只鴨子的圖片制造認(rèn)知沖突：這幅圖左右兩部分也是完全一樣的，它是軸對(duì)稱圖形嗎？由此觸發(fā)學(xué)生的“對(duì)折”思維，打破“完全一樣”給概念理解帶來的認(rèn)知不完整性的影響。學(xué)生在活動(dòng)中感悟得出“對(duì)折后完全重合”的圖形才能被判定為軸對(duì)稱圖形（如圖1），同時(shí)理解和明確“折痕”即對(duì)稱軸，并感悟“對(duì)折”對(duì)于軸對(duì)稱的重要意義。

“動(dòng)”的經(jīng)驗(yàn)可以給“想”帶來無限的空間，學(xué)生經(jīng)歷了大量“對(duì)折”的操作活動(dòng)后，能形成幾何變換的初始概念。他們不僅有了圖形對(duì)稱的直覺，也有了圖形會(huì)動(dòng)的直覺，那些在作業(yè)本上、屏幕上的圖形雖不能進(jìn)行具體的操作，卻可以在腦海中“折”。然而，此時(shí)學(xué)生只是把圖形的重合理解成面的相等，不會(huì)認(rèn)識(shí)到是點(diǎn)到點(diǎn)距離的相等。

二、適配“對(duì)折”到“不折”的心理跨越

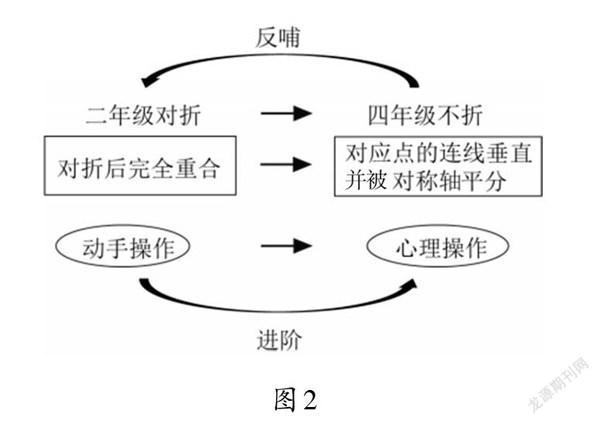
四年級(jí)《軸對(duì)稱》教學(xué)，是在對(duì)折的基礎(chǔ)之上進(jìn)一步滲透軸對(duì)稱的性質(zhì)，注重思想和方法的感悟。教師要引導(dǎo)學(xué)生在“不折”的前提下找到并能標(biāo)準(zhǔn)地畫出軸對(duì)稱圖形的對(duì)稱軸，發(fā)現(xiàn)軸對(duì)稱的特點(diǎn)：對(duì)應(yīng)點(diǎn)的連線與對(duì)稱軸垂直并被對(duì)稱軸平分。最后，利用性質(zhì)驗(yàn)證“對(duì)折”操作為什么能判定圖形是否為軸對(duì)稱圖形，達(dá)到反哺的效果（如圖2）。

然而，當(dāng)教師提問：你是怎么找到對(duì)稱軸的？不少學(xué)生還是回答“因?yàn)閷?duì)折后完全重合”，思維依舊停留在二年級(jí)水平。根據(jù)范希爾理論中的進(jìn)階性，學(xué)生幾何思維水平的提升是由教學(xué)決定的，而不是隨年齡成長(zhǎng)或心理成熟自然而然發(fā)生的。學(xué)生在理解“軸對(duì)稱”概念的進(jìn)階過程中表現(xiàn)出思維的不連續(xù)性，也就說明從“折”到“不折”兩個(gè)水平的過渡不是自然的，而是一個(gè)“跨越”的過程。當(dāng)教學(xué)高于學(xué)生的思維層次時(shí)，必定導(dǎo)致學(xué)生無法理解，即產(chǎn)生不適配性。為了適配，教師應(yīng)設(shè)計(jì)教學(xué)環(huán)節(jié)讓學(xué)生經(jīng)歷從動(dòng)手操作到心理操作（想象）的過程，為學(xué)生“跨越”助一臂之力。

【片段1】

教師出示圖3。

教師提問：這些是我們二年級(jí)時(shí)已認(rèn)識(shí)的軸對(duì)稱圖形，大家都能用“對(duì)折”的方法找對(duì)稱軸。今天老師把它們放在大屏幕中，不能對(duì)折了，你還能找到對(duì)稱軸嗎？（讓學(xué)生想象對(duì)稱軸在哪里，讓他們指一指）

教師追問：怎樣才能準(zhǔn)確地找到對(duì)稱軸的位置呢？

（讓學(xué)生用自己喜歡的方式，畫出它們的對(duì)稱軸）

開場(chǎng)說明同樣的“對(duì)稱圖形”二年級(jí)用“對(duì)折”的方法找對(duì)稱軸，四年級(jí)要求“不折”找對(duì)稱軸。這樣不同的要求，為學(xué)生從動(dòng)手操作過渡到心理操作提供腳手架，引導(dǎo)他們的思維從單向低層次向多元高層次發(fā)展。

三、挖掘“相等”并“垂直”的完整內(nèi)涵

學(xué)生在二年級(jí)時(shí)積累的直觀經(jīng)驗(yàn)是“面的相等”，即圖形的“完全重合”。在這樣的基礎(chǔ)上，教師如果借助格子圖，學(xué)生就容易從“面的相等”過渡到“對(duì)應(yīng)點(diǎn)到對(duì)稱軸的距離相等”，但很少有學(xué)生能夠發(fā)現(xiàn)“對(duì)應(yīng)點(diǎn)與對(duì)稱軸垂直”。

（一）適度增加，“自”畫蘊(yùn)垂

根據(jù)諾曼和魯梅爾哈特的研究，“增加”是思維轉(zhuǎn)變方式的其中一種，即在既有的知識(shí)模塊中不改變?cè)薪Y(jié)構(gòu)而增加新知識(shí)。以下教學(xué)片段中，教師在學(xué)生自主畫對(duì)稱軸的基礎(chǔ)上，利用“相等”的經(jīng)驗(yàn)去追加問題，層層遞進(jìn)，意蘊(yùn)“垂直”。

【片段2】

1.教師出示圖4，提問：你是怎么畫出對(duì)稱軸的？

（學(xué)生指出找到了兩個(gè)關(guān)鍵的點(diǎn)來畫垂線）

2.教師出示圖5，提問：只有一個(gè)關(guān)鍵點(diǎn)，你又是怎么畫出對(duì)稱軸的呢？

預(yù)設(shè)一：量一量，再找一個(gè)點(diǎn)。

預(yù)設(shè)二：用畫垂線的方法也能畫出對(duì)稱軸。

3.教師出示長(zhǎng)方形，提問：你又是怎么畫出它的對(duì)稱軸的呢？（如圖6）

（學(xué)生根據(jù)圖5的經(jīng)驗(yàn)，除了用尺子量，還用了畫垂線的方法）

師生小結(jié)：畫垂線的方法很實(shí)用。

準(zhǔn)確了解學(xué)生遇到的認(rèn)知障礙是教學(xué)中做到“對(duì)癥下藥”的前提。引導(dǎo)學(xué)生理解，在畫對(duì)稱軸時(shí)緊緊抓住軸對(duì)稱圖形的關(guān)鍵點(diǎn)或者把邊平均分成兩份，同時(shí)借助畫垂線的方法，就能標(biāo)準(zhǔn)地畫出對(duì)稱軸。這樣就提前埋好了“垂直”的種子，使其后續(xù)得以生根發(fā)芽。

（二）合理調(diào)整，單“等”無垂

從單一的“相等”感性認(rèn)知調(diào)整為“相等并垂直”的理性認(rèn)知，是學(xué)生思維結(jié)構(gòu)變化的體現(xiàn)，也是數(shù)學(xué)教學(xué)本質(zhì)的要求。以下教學(xué)片段中，教師對(duì)學(xué)生的思維進(jìn)行加工、改造。學(xué)生在思維順暢后就能突破沖突，在辨析、歸納中深刻體會(huì)到：除了相等，“對(duì)應(yīng)點(diǎn)”還應(yīng)基于連線垂直于對(duì)稱軸來確定（如圖7）。

【片段3】

師：仔細(xì)觀察，對(duì)稱軸的左邊和右邊有什么特點(diǎn)呢？請(qǐng)你找一找，描一描，連一連。

生：我發(fā)現(xiàn)對(duì)稱軸的兩邊都是一模一樣的，并且對(duì)應(yīng)點(diǎn)到對(duì)稱軸的距離都相等。

（教師根據(jù)學(xué)生回答，把每個(gè)特殊點(diǎn)都指一遍）

小結(jié)：從對(duì)稱軸的兩邊找到點(diǎn)的對(duì)應(yīng)關(guān)系是好辦法，那么我們從上往下依次來找。

教師把“垂直”暫時(shí)“架空”，意圖在于讓學(xué)生先理解“對(duì)應(yīng)點(diǎn)”，便于下一環(huán)節(jié)集中火力探究“垂直”。緊接著，通過找特殊點(diǎn)和非特殊點(diǎn)的對(duì)應(yīng)點(diǎn)，引導(dǎo)學(xué)生感悟：對(duì)稱軸一邊的任意一點(diǎn)，都能在另一邊上找到它的對(duì)應(yīng)點(diǎn)，且在實(shí)際中，只要找關(guān)鍵點(diǎn)就行了。

（三）設(shè)置矛盾，對(duì)“比”引垂

有效的調(diào)整是完整、系統(tǒng)地掌握軸對(duì)稱的關(guān)鍵。教師通過設(shè)置矛盾，引導(dǎo)學(xué)生在對(duì)比中實(shí)現(xiàn)思維斷層的聯(lián)結(jié)。

【片段4】

教師組織學(xué)生討論圖9。

師：點(diǎn)E′到對(duì)稱軸的距離也是1格，為什么它不是點(diǎn)C的對(duì)應(yīng)點(diǎn)？

生：這兩點(diǎn)的連線與對(duì)稱軸不垂直。

教師追問：對(duì)應(yīng)點(diǎn)除了到對(duì)稱軸的距離要相等外，還要滿足什么要求？

生：連線要與對(duì)稱軸垂直。

師：一個(gè)點(diǎn)不能說明問題，我們?cè)俣嗾規(guī)讉€(gè)點(diǎn)，看看它們的連線。

師：每一組對(duì)應(yīng)點(diǎn)都是“距離相等，連線垂直”。

小結(jié)：對(duì)應(yīng)點(diǎn)不僅到對(duì)稱軸的距離相等，并且連線與對(duì)稱軸垂直。

C′和E′的同時(shí)存在，容易使學(xué)生把問題聚焦到這兩點(diǎn)與點(diǎn)C的連線上來。線段CC′與CE′同時(shí)相連，自然就把學(xué)生的思維從“相等”引導(dǎo)到“垂直”的層面上來。接下來，教師展示開場(chǎng)時(shí)的另兩幅圖，讓學(xué)生利用“垂直”的思維方式找對(duì)應(yīng)點(diǎn)，鞏固軸對(duì)稱的特點(diǎn)。

【片段5】

教師出示圖10。

師：請(qǐng)看這三幅圖，通過畫對(duì)稱軸和找軸對(duì)稱的特點(diǎn)，你學(xué)會(huì)了什么？

生：對(duì)應(yīng)點(diǎn)到對(duì)稱軸的距離相等，連線與對(duì)稱軸垂直。

師：畫對(duì)稱軸的時(shí)候，還可以用畫垂線的方法，它的原理其實(shí)就是“相等并垂直”。

教師在教學(xué)時(shí)要將所教內(nèi)容置于整體設(shè)計(jì)的知識(shí)結(jié)構(gòu)中，讓學(xué)生進(jìn)行系統(tǒng)地思考。畫對(duì)稱軸和軸對(duì)稱的性質(zhì)之間有著緊密的聯(lián)系，教師可以通過“垂直”把它們聯(lián)系起來，從而實(shí)現(xiàn)教學(xué)的一致性。

四、重建“定性”到“定量”的原理閉環(huán)

要使學(xué)生深度理解“對(duì)應(yīng)點(diǎn)的連線與對(duì)稱軸垂直并被對(duì)稱軸平分”的緣由，教師還需設(shè)計(jì)教學(xué)環(huán)節(jié)，讓學(xué)生經(jīng)歷“重建”的過程，也就是讓學(xué)生重新審視以往的軸對(duì)稱圖形，對(duì)其進(jìn)行再思考、再構(gòu)建，以獲得對(duì)軸對(duì)稱的原理閉環(huán)。

（一）重建一：常見圖形對(duì)稱軸條數(shù)

【片段6】

質(zhì)疑：為什么正方形有4條對(duì)稱軸，而一般的長(zhǎng)方形（不包含正方形）只有2條？

師：我們先來研究正方形，重點(diǎn)來分析兩條斜的對(duì)稱軸。

以相對(duì)的頂點(diǎn)為對(duì)應(yīng)點(diǎn)，連線垂直，所以正方形的對(duì)角線是它的對(duì)稱軸，另一條對(duì)角線也同理可得。

師：長(zhǎng)方形（不包含正方形）的對(duì)角線，是不是它的對(duì)稱軸呢？以相對(duì)頂點(diǎn)為對(duì)應(yīng)點(diǎn)，連線，你發(fā)現(xiàn)了什么？

生：與對(duì)角線相互不垂直。

師：它們雖然長(zhǎng)度相等，但不垂直，所以這條對(duì)角線不是長(zhǎng)方形的對(duì)稱軸。

小結(jié)：軸對(duì)稱的性質(zhì)可以解決以前只能靠對(duì)折才能解決的問題。

教學(xué)不應(yīng)只局限于讓學(xué)生學(xué)會(huì)畫對(duì)稱軸，也應(yīng)解釋為什么要這樣畫，讓學(xué)生知其所以然。本環(huán)節(jié)從常見的長(zhǎng)方形、正方形入手，利用軸對(duì)稱的性質(zhì)進(jìn)行解釋說明，反哺以前的直觀認(rèn)知，讓對(duì)稱軸的條數(shù)變得有理有據(jù)，使“相等并且垂直”在軸對(duì)稱中一脈相承。

（二）重建二：常見圖形的性質(zhì)屬性

學(xué)生對(duì)于軸對(duì)稱的“惑”主要是：某些擁有兩部分完全相同的圖形卻不是軸對(duì)稱圖形。其中最典型的屬平行四邊形（不包括菱形、長(zhǎng)方形、正方形，下同）。平行四邊形有相等的邊和角，且任一條對(duì)角線或以任一邊的中點(diǎn)出發(fā)作鄰邊的平行線，都可以將其分成相同的兩部分，因此容易被錯(cuò)認(rèn)為是軸對(duì)稱圖形。事實(shí)上，平行四邊形屬于中心對(duì)稱圖形。中心對(duì)稱圖形有兩個(gè)特征：一是所有對(duì)應(yīng)點(diǎn)連線交于一點(diǎn)，且各對(duì)應(yīng)點(diǎn)到該交點(diǎn)距離相等；二是繞交點(diǎn)旋轉(zhuǎn)180°后可以跟原圖形完全重合，這個(gè)交點(diǎn)稱為對(duì)稱中心。中心對(duì)稱與軸對(duì)稱同屬圖形的變換，但兩者的變換方式不同。

深度認(rèn)識(shí)圖形的本質(zhì)屬性，審視教學(xué)內(nèi)容，有利于教師合理開展教學(xué)活動(dòng)，針對(duì)學(xué)生出現(xiàn)的錯(cuò)誤，提供診斷教學(xué)策略，并有效地對(duì)學(xué)生的認(rèn)知偏移進(jìn)行診斷、糾正，從而根除學(xué)生的錯(cuò)誤觀念。

【片段7】

師：如果以長(zhǎng)方形的對(duì)角線作為對(duì)稱軸畫圖形，會(huì)是一個(gè)怎樣的軸對(duì)稱圖形呢？根據(jù)相等且垂直的原理，補(bǔ)全這個(gè)軸對(duì)稱圖形的另一半。（用課件動(dòng)態(tài)演示過程，如圖11）

師：現(xiàn)在這樣一個(gè)普通三角形，請(qǐng)你先自己規(guī)定一條對(duì)稱軸，然后再創(chuàng)造出軸對(duì)稱圖形。

（展示不同的學(xué)生作品，如圖12）

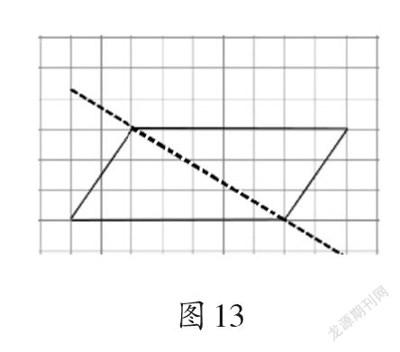
教師出示圖13。

師：看這一幅，創(chuàng)造對(duì)了嗎？能用今天學(xué)的知識(shí)來解釋一下嗎？

生：相對(duì)頂點(diǎn)的連線與他畫的對(duì)稱軸不垂直。

師：這正好也解釋了為什么平行四邊形不是軸對(duì)稱圖形。對(duì)應(yīng)點(diǎn)的連線與“軸”不垂直，就不是軸對(duì)稱圖形。

學(xué)生感悟到對(duì)于同一個(gè)圖形，通過不同的對(duì)稱軸會(huì)形成不同的軸對(duì)稱圖形。教師要培養(yǎng)學(xué)生多角度思考問題的能力，發(fā)展其想象力。教師利用“相等且垂直”原理，通過對(duì)以往熟悉的圖形進(jìn)行重新審視，完成了軸對(duì)稱性質(zhì)的第二次反哺——判定平行四邊形是否為軸對(duì)稱圖形。

“相等且垂直”使“軸對(duì)稱”內(nèi)容形成了一個(gè)高度融合的有機(jī)整體，它不僅是軸對(duì)稱性質(zhì)的具體體現(xiàn)，更是用來反哺、判定軸對(duì)稱性質(zhì)的有力工具，是概念學(xué)習(xí)本質(zhì)化、系統(tǒng)化、結(jié)構(gòu)化的精髓所在。

參考文獻(xiàn)：

［1］鮑建生，周超.數(shù)學(xué)學(xué)習(xí)的心理基礎(chǔ)與過程［M］.上海：上海教育出版社，2009.