基于分離障礙物的地下車庫車位排布算法

馮嘉宇，王瀟霆，沈 煒

（浙江理工大學 信息學院，杭州 310018）

0 引言

城市車位短缺是制約現代城市發展的新問題［1］。地下車庫為緩解車位短缺提供了一個成本更低的方案［2］，廣大開發商也開始研究如何在地下車庫中排布才能得到更多的車位［3］，以獲取更高的經濟效益。目前，地下車庫的車位排布仍以人工設計為主，但是由于外邊界不規則和內部的障礙物等問題［4］，人工設計的效率較低。因此，一些專家學者開始將自動化設計運用于解決地下車庫的車位排布問題。

車位排布算法和工業生產中的二維排樣算法很相似。早在1981 年，Fowler 等［4］就已證明了不帶約束條件的排樣問題是NP 完全問題。因此，在排樣問題基礎上添加了更多約束條件的車位排布問題也是一個NP 完全問題。對于車位排布問題，現存的多數算法都是從傳統排樣問題中優化得到的。Abdelfatah 等［5］提出了一種適用于矩形區域的設計線性規劃模型，并考慮了車道夾角；Kong 等［6］通過調整車位的長和寬，運用混合整數非線性模型計算車位長和寬的變化對于最終可排列車位數量的影響；Huang 等［7］設計了一套基于模擬退火算法的矩形區域內車位排布問題的通用算法；Syahrini 等［8］則通過線性規劃模型設計了一套適用于三角形區域的車位排列算法；Ihda 等［9］提出了一種適用于平行四邊形區域的線性規劃模型；Ferreira 等［10］設計了一種車位平行疊放的排布方式，用于優化矩形高密度停車場的車位排布；Timpner 等［11］提出了停車空間優化模型；Banzhaf 等［12］通過建立混合整數規劃模型，將普通停車場改造為高密度停車場；Nourinejad 等［13］使用排隊論構建了混合整數模型，并通過benders 分解算法進行車位排布。但是，上述這些研究都集中于地表停車場，而沒有考慮障礙物的約束。

對于帶障礙物約束的地下車庫的排列研究，徐涵喆［14］等設計了一種基于遺傳算法的外圈車位排布啟發式算法。黃逸彬等［15］則通過對不規則停車場區域進行圖形分割后，運用粒子群算法進車位排布。利潤等［16］通過網格化，將原問題區域劃分為多個可應用排布算法的子區域，提出了一種基于貪婪分割的地下車位排布算法。但是這些研究者都沒有充分利用到每棟樓中承重墻之間的空間，同時車位與邊界、障礙物之間存在的夾角也造成了大量的面積浪費。

為了充分利用停車場空間，盡可能最大化車位數量，本文提出了一種根據內部障礙物位置劃分為內圈和外圈之后，再對兩個區域進行分離處理的啟發式自動化排布算法。該算法可以適用于內部障礙物大致平行的任意不帶曲邊的地下車庫；可以通過計算合理排布車位、車位和承重柱的位置；可以將排布結果可視化呈現，輔助人工設計。

1 問題描述

車位排布問題通過輸入一個地下車庫的外邊界和內部所有的障礙物，需要在滿足約束條件的情況下，實現車位數量的最大化。

1.1 約束條件

地下車庫車位排布的約束條件，在傳統排樣問題基礎上，根據車位排布場景的特殊性，其主要約束條件為：

（1）外邊界約束：任意車位模塊、車道不得超過外邊界所包含的范圍。

（2）內部障礙物約束：任意車位模塊、車道不得與內部障礙物重疊。

（3）車位與車道分離的約束：車位模塊不能與車道重疊。

（4）連通性約束：必須保證每個車位可以駛入車道，所有車道之間必須相互連通。

由于約束條件4 中的入口和出口需要在車位排布完成之后由人工確定，故本文只需保證各個車位模塊之間有車道連通即可。

1.2 約束條件的數學模型

地下車庫的外邊界可以用一個點的集合Pborder＝｛（x1，y1），（x2，y2），…，（xn，yn）｝，構成一個封閉的多邊形Sborder。在地下車庫內，存在多個多邊形表示的內部障礙物Tbar ＝｛T1，T2，…，Tm｝，每個內部障礙物也由一個點的集合構成＝｛（x1，y1），（x2，y2），…，（xn，yn）｝。

外邊界和內部障礙物作為輸入條件，滿足：

定義Pm為車位的集合，R為車道的集合，則存在如下約束：

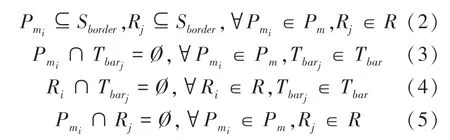
其中，式（2）表示外邊界約束；式（3）、式（4）表示內部障礙物約束；式（5）表示車位與車道分離的約束。

車道集合R ＝｛R1，R2，…，Rm｝ 是由多個多邊形組成的集合。車道的連通需要通過不同車道之間的相交來實現，所以對于所有的車道，需滿足：

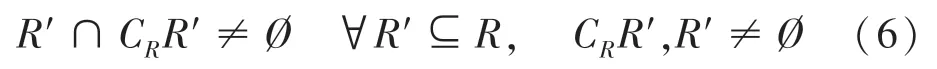
同時每個車位必須有車道相鄰接。對于表示任意車位的矩形ABCD，將其四邊向外延長車位寬度β，如圖1 所示。延長后滿足：

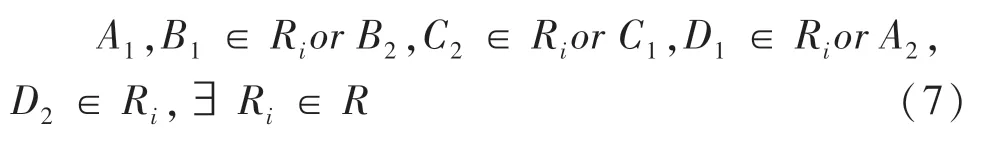
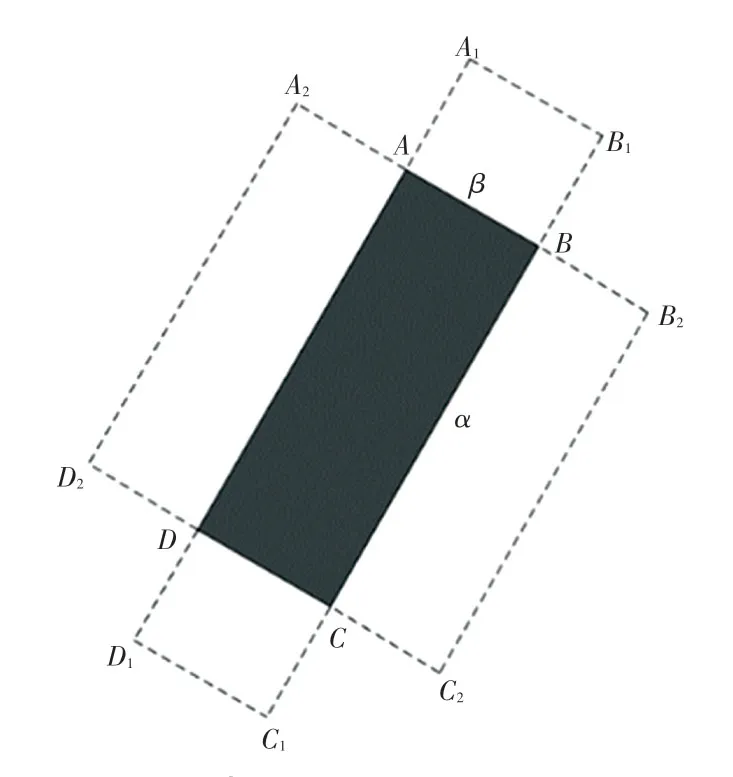
圖1 車位向外延長Fig.1 Parking Spaces extend outwards

1.3 車位模塊

車位模塊是由在同一方向上鄰接同一車道的車位排列形成的平行四邊形，按照傾角的不同，可以分為 0°、30°、45°、60°、90° 和垂直式［17］。IL Chodash［18］等人通過分析0°、30°、45°、60°、90°5 種不同角度的停車位在現實停車場中的表現，發現90°的車位模塊在67%的場景中都可以保證車位數量的最大化。趙志強［19］等用車道面積與車位面積衡量車位實際占用面積，發現90°的車位模塊占用面積最少。綜合這些結論，本文在車位排布中主要采用90°的車位模塊，在寬度不夠時采用0°的車位模塊。

車位模塊中采用每若干個車位之間設置承重柱的方式構建柱網。其中，兩個相鄰承重柱之間的車位數量取決于承重柱的最大間隔。車位模塊中的每個車位都是長為α、寬為β的矩形，對于承重柱的最大間距d，在90°的車位模塊中需要在每個車位之間插入一個承重柱，0°的車位模塊則為

1.4 算法流程

本文提出的算法，主要分為以下4 個階段：

（1）劃分內外區域：根據外邊界和內部障礙物的坐標，用矩形包裹所有障礙物后，劃分為矩形內部和矩形外部。

（2）矩形內部區域車位排布：通過像素分割柵格化內部區域［20］并建立矩陣；通過矩陣計算，得到矩形內部區域車位數量最多的排布方案，并保證與外部區域連通。

（3）矩形外部區域車位排布：對矩形外部區域進行分割，使用遺傳算法計算得到矩形外部區域車位數量最多的排布方案。

（4）車位坐標計算和可視化：根據車位模塊的位置，計算車位坐標。

本文主要對第1 和第2 階段進行研究，第3 階段矩形外部區域的車位排布，主要參考徐涵喆［16］等提出的遺傳算法排布方案，第4 階段車位模塊的坐標則通過遍歷計算得到。

2 模型建立

2.1 內部矩陣構建

設定一個長和寬均平行或垂直于內部障礙物的最小矩形Srec，使得Tbar?Srec，則矩形外部區域Soutside為：

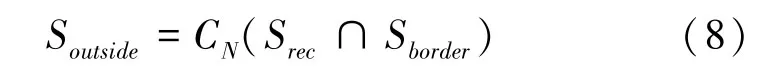
記Srec平行于x軸方向的邊長為a，平行于y軸方向的邊長為b，左上角頂點的坐標為（x0，y0）。按照分割精度δ分割Srec上的點，可以得到所有點坐標的集合Prec：

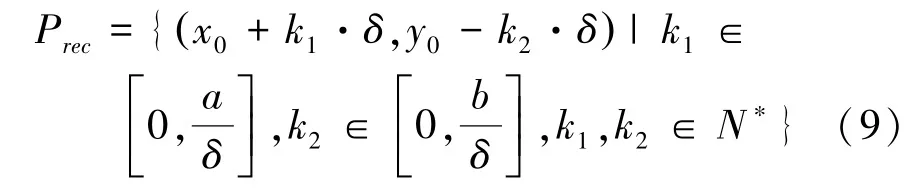
構建初始矩陣A0，其中所有元素滿足：

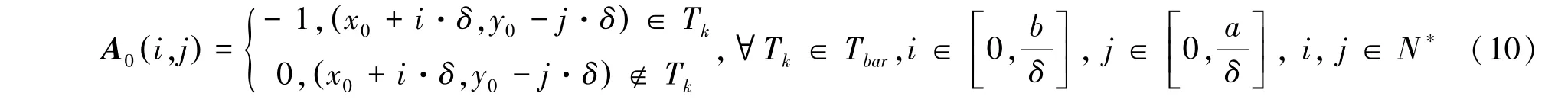
根據A0中的元素值，得到A(i，j)，i∈

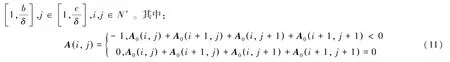
矩陣A即為描述矩形內部區域的模型。其中-1 表示有障礙物，0 表示空曠。

2.2 分割精度選擇

在判斷每個正方形是否空曠時，因為不包含任何障礙物才認為是空曠的，所以存在一定的面積損失［19］。例如：對于長6 m、寬2.5 m 的停車位來說，δ為0.5 m 時每個正方形損失會占單車位1／60 的面積，δ為0.25 m 時占1／240。所以δ越小，損失的正方形面積也越小。但是，當δ縮小時，所需計算次數和內存是以O（n2）復雜度增長，導致計算效率的下降。

為了選擇合適的δ值，在考慮整除特性的基礎上，選擇1 cm、2 cm、5 cm 3 種不同的分割精度，對3張不同的地下車庫圖紙在i7 9750H 處理器、16 GB內存環境下進行了分割實驗。根據實驗結果，為兼容一般計算機的性能，最終決定δ取5 cm。

2.3 外圈的凹角處理

矩形外部區域Soutside中不包含任何障礙物，所以只用遺傳算法就可以計算。遺傳算法的關鍵在于對Soutside中外邊界點集Pborder的凹角分割策略。參考劉彥鵬等［21］提出的簡單多邊形剖分算法，若凹角范圍在采用作垂線的方式切割；在內，采用作延長線的方式切割。因為每個凹點均存在兩條對應邊，所以存在兩種不同的切割策略，可得到m ＝2n。其中，n為Pborder凹點的數量。

3 算法設計

3.1 內部矩形中主樓內部空隙排布

定義最小閉包矩形為包裹每棟主樓的且平行于坐標軸的最小矩形。記地下車庫中主樓的閉包矩形集合為B ＝｛B1，B2，…，Bn｝，滿足：

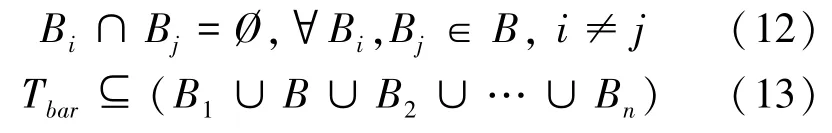
式（12）表示各個矩形之間不存在重疊，式（13）表示在這些矩形之外不存在其它障礙物。每個矩形可以包含4 個點的點集PB ＝｛（x1，y1），（x2，y1），（x2，y2），（x1，y2）｜x1＜x2，y1＞y2｝。每棟樓空隙的車位排列算法流程如下：

輸入矩陣A，矩陣左上角元素的坐標（x0，y0），主樓的包裹矩形集合B，車位長寬α、β，主樓數量n

輸出車位集合L1，修改后的矩陣A

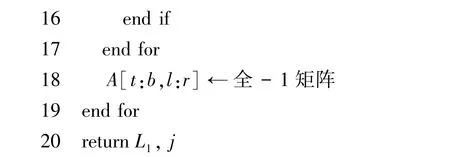
經該流程處理后，得到如圖2 所示的可視化結果。

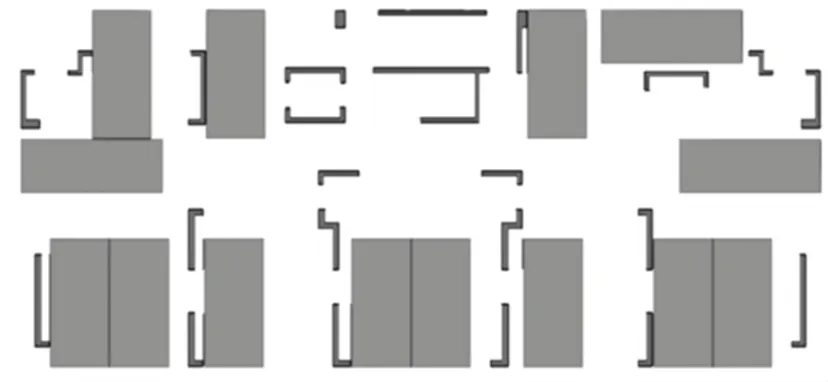
圖2 一棟樓內空隙中的車位排布Fig.2 The arrangement of parking Spaces in the voids of a building

3.2 內部矩形中主樓內部空隙排布

對于矩陣A，給出如下定義：

定義1若Z?A且Z ＝0，則稱Z為A的全0子矩陣。用全0 子矩陣中元素的個數來表示矩陣的大小，對應矩形的面積。

定義2若對于A的全零子矩陣Zm，不存在另一個全0 子矩陣Z0使得Zm?Z0，則稱Zm為A的極大全0 子矩陣。

定義3若一個矩形內不包含任何障礙物，則稱其為全空矩形。

定義4在內部矩形區域內，若對于一個全空矩形，不能被任何一個其它的全空矩形完全包裹，則稱其為極大全空矩形。

對于全空矩形內的車位排布，可以充分利用矩形的直角特性［22］，采用兩排90°的車位模塊間隔一條過道的模式依次循環，在不足時采用0°的車位模塊代替，如圖3 所示。

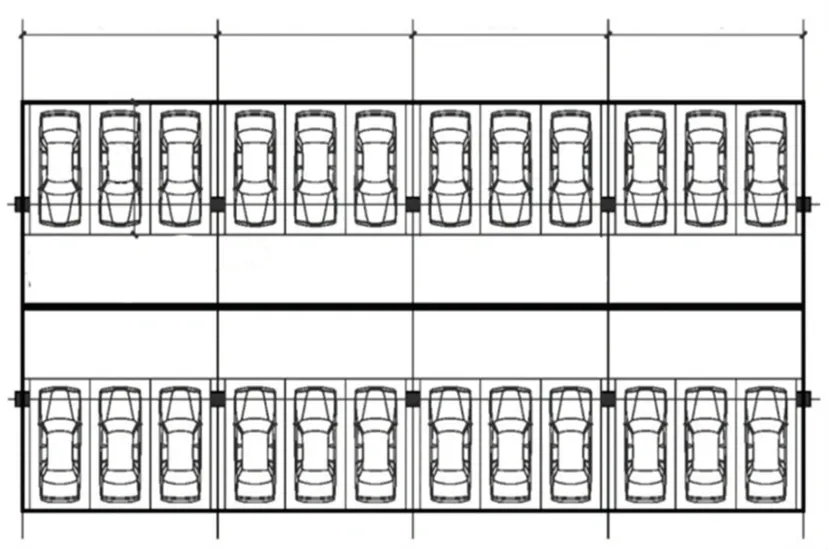
圖3 矩形區域內的車位模塊設置Fig.3 Parking Spaces extend outwards

內部矩形中剩余部分的車位排布算法流程如下：

輸入上一步修改后的矩陣A，矩陣左上角元素的坐標（x0，y0），車位長寬α、β，車位集合L1

3.3 矩形外部排布

矩形外部使用遺傳算法對于每一切割區域進行計算，并考慮計算結果造成的L1、L2中車位堵塞損失，計算得到每種切割方案可排布車位數后，取其中車位數量最多的切割方案。

對于與車道集合R1有重合部分的車位模塊，根據車道切割成若干子車位模塊之后，計算車位的坐標。最終可以得到矩形外部排布的車位集合L3和車道集合R2。

4 實例驗證

為驗證基于分離障礙物的地下車庫車位排布啟發式算法的效果和計算速度，對5 張不同的地下車庫圖紙進行計算。采用4 核、3.40 GHZ 處理器、內存為16 GB 的計算機進行實驗，矩形內部區域分割精度δ為5 cm，車道和車位模塊長度均為6 m，承重柱邊長0.5 m，編程語言為python3.8.1。得到的計算結果見表1。

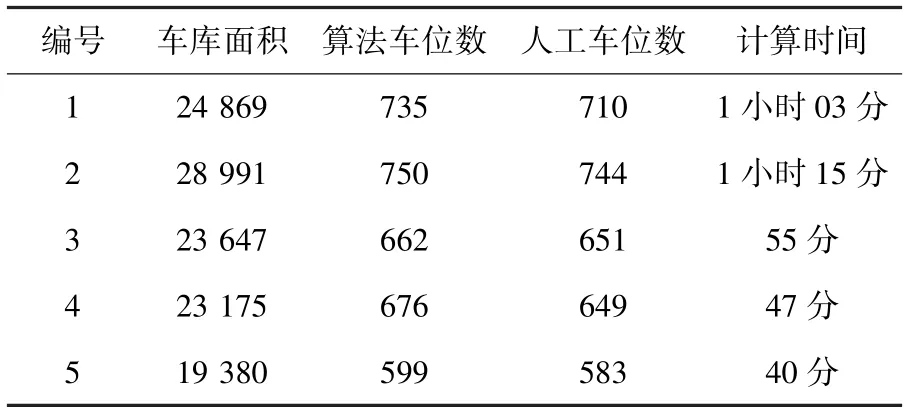
表1 圖紙運算結果Tab.1 Drawing Operation Result

上述結果中，算法計算得到的結果總體上優于人工排列的結果。如果考慮后續人工對車道設置的繼續優化，仍有較優的結果。其中，圖紙4 算法和人工排布結果如圖4、圖5 所示。

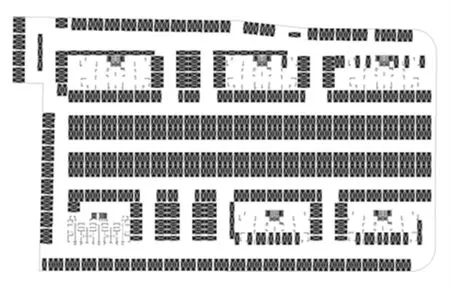
圖4 圖紙4 算法排布結果Fig.4 Result of algorithm arrangement in Drawing 4

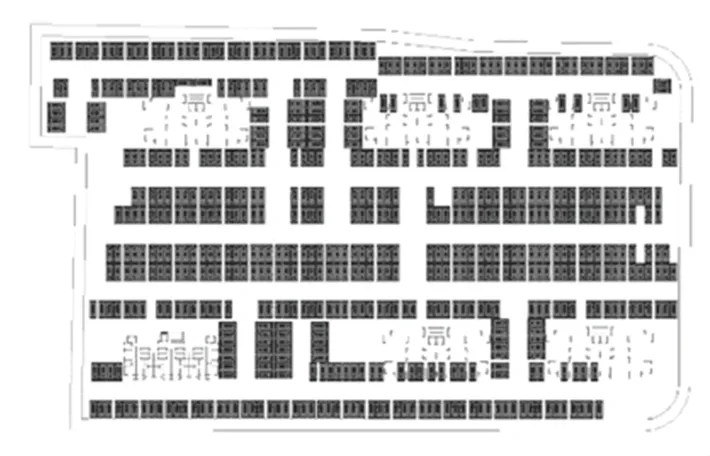
圖5 圖紙4 人工排布結果Fig.5 Result of manual arrangement in Drawing 4

5 結束語

本文算法對地下車庫按照障礙物進行了區域分割，分別用像素分割和遺傳算法兩種啟發式的求解方法，計算得到了內外區域的排布方案，對比人工排列的實際工程圖紙，可以得出如下結論：

（1）通過對矩形內部區域進行像素分割，將復雜的內部障礙物用矩陣元素表示，且充分利用了車位、車位模塊、車道中平行和垂直的特性；創造性地利用了每棟樓中的空隙區域，并通過對稱、反轉每個極大全空矩形中的最優排布方案，保證矩形內部車位總數量的最大化。

（2）通過解決矩形內外結合部區域的連通性問題，可以保證全局的車位數量最大化；比較方便更改車位、道路等長寬參數，可以滿足人工對于車位尺寸等的不同需求；該算法可以在較快的時間內完成車位的排布和坐標計算，為人工排列提高效率，增加地下車庫有限區域內的車位數量。

（3）車位的坐標以可視化呈現，為人工排列車位提供一定的參考依據，節省了人工排列的時間。