2022年高考全國甲卷圓錐曲線試題探究與變式

四川省成都市石室中學 (610015) 李賢江 成都市電子科技大學實驗學校 (611731) 黃 信

圓錐曲線一些解答題常常含有極點與極線的背景.極點與極線是高等幾何的重要理論，是解決圓錐曲線一些復雜問題的巧妙方法.學生如果了解極點與極線理論，那么就可預知結果并且減少大量繁瑣運算.

極點與極線的定義：如圖1，圓錐曲線外一點S，過點S作圓錐曲線的兩條割線SA和SC，分別交圓錐曲線于A、B，C、D四點，直線AD和BC交于點E，直線AC和BD交于點T，直線ST是點E關于該圓錐曲線的極線.

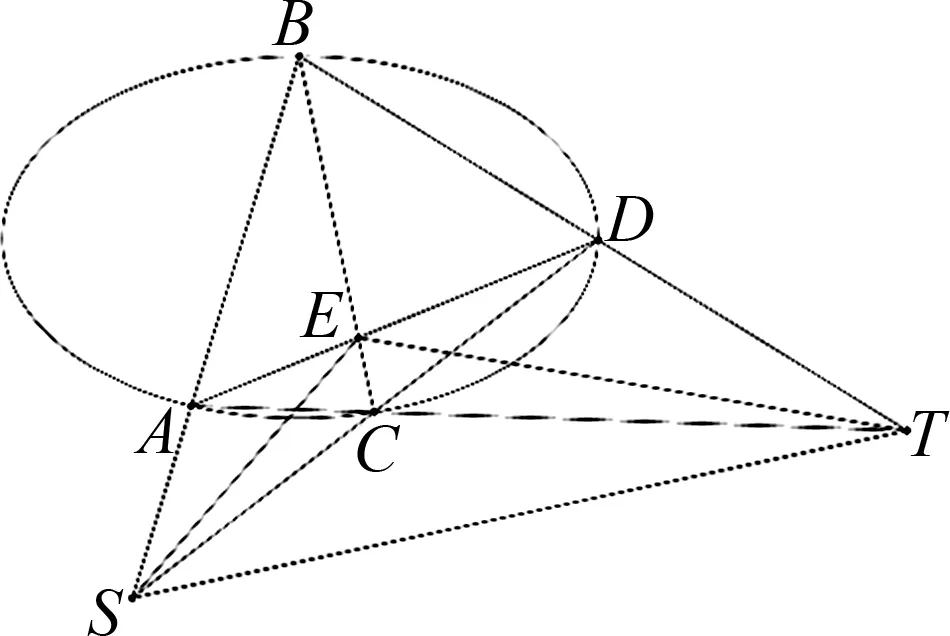
圖1

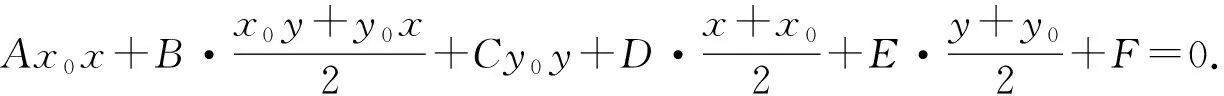
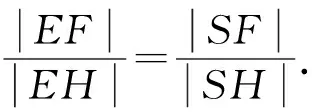
圖2

例1 (2022高考數學全國卷甲卷理科改編)過拋物線y2=4x的焦點F的直線交拋物線于M,N兩點，D(2,0)，MD交拋物線于另一點A，ND交拋物線于另一點B，設直線AB、直線MN的傾斜角分別為α,β，當α-β取最大值時，求直線AB的方程.

圖3

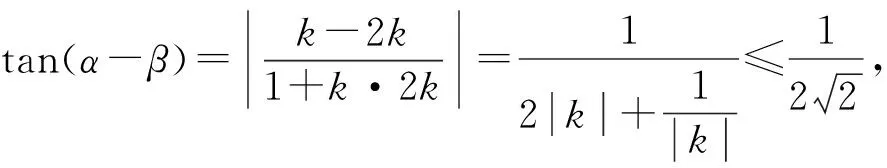
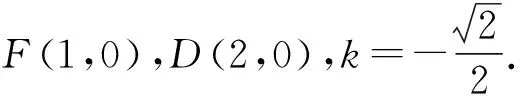
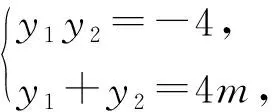
以高等幾何中的極點與極線為背景命制的解析幾何試題很多，認識這類問題有助于以高觀點把握問題，將問題看得更為透徹，下面給出例1的兩個變式.

圖4

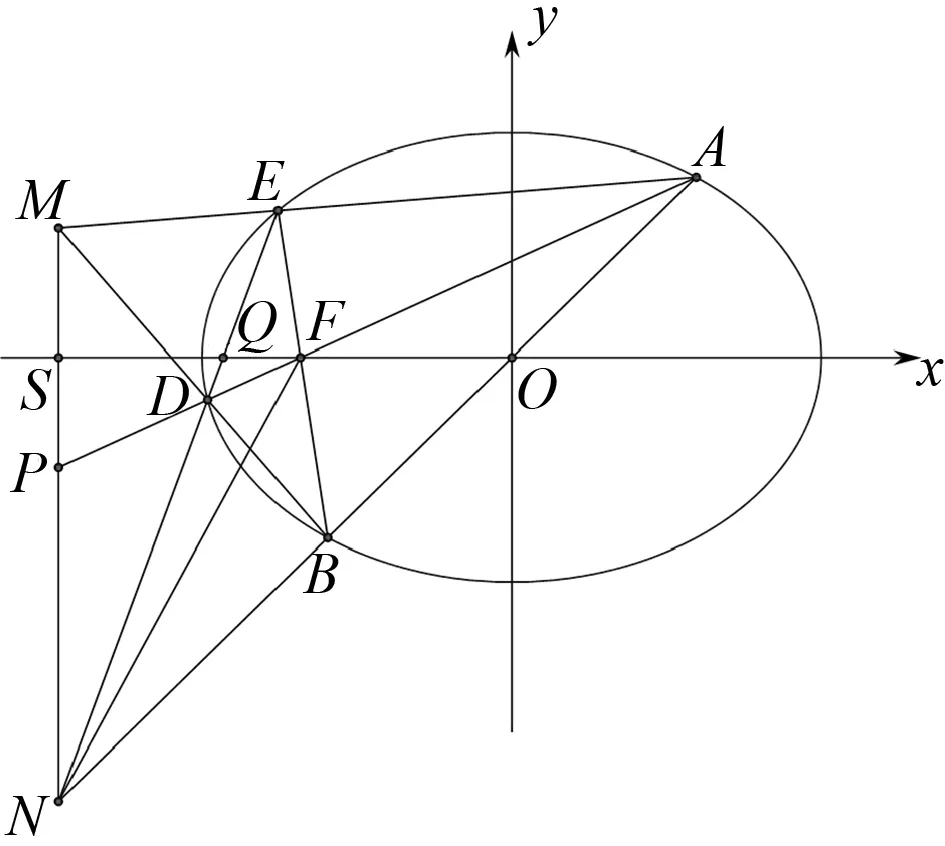
圖5

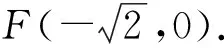
圖6

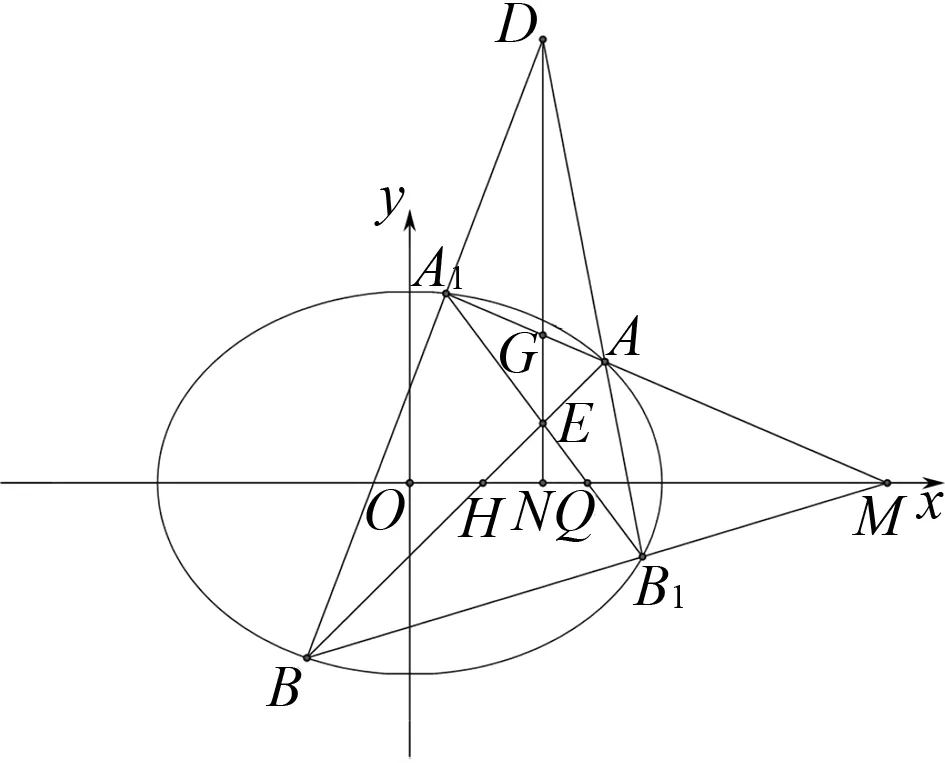
圖7

說明：變式2的結論與直線AB、直線A1B1的交點E在橢圓內、外無關，也與E在x軸的上方、下方無關.