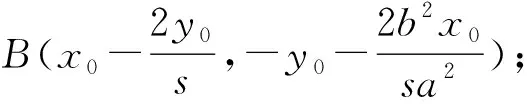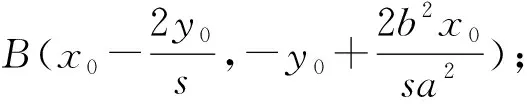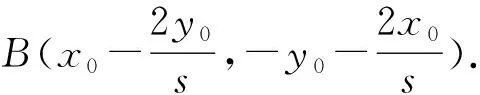對(duì)“一道高考圓錐曲線題中的定點(diǎn)問(wèn)題”再探究

聊城大學(xué)數(shù)學(xué)科學(xué)學(xué)院 (252000) 徐茂林 房元霞

一、原題呈現(xiàn)

(1)求C的方程；

(2)設(shè)直線l不經(jīng)過(guò)P2點(diǎn)且與C相交于A，B兩點(diǎn).若直線P2A與直線P2B的斜率的和為-1，證明：l過(guò)定點(diǎn).

二、文獻(xiàn)[1]中的結(jié)論

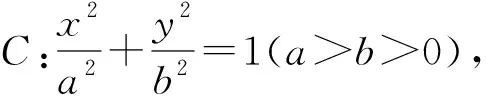
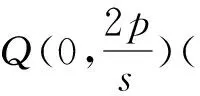
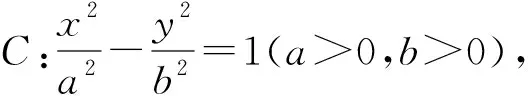
兩條直線恒過(guò)圓錐曲線上的固定點(diǎn)，如果這個(gè)點(diǎn)是圓錐曲線上任意一點(diǎn)，會(huì)有一般的結(jié)論嗎？帶著這個(gè)問(wèn)題，我們先用GeoGebra軟件進(jìn)行了探索，歸納出一般結(jié)論后再例行證明，如下是我們探究的結(jié)論.

三、再探究

(一)橢圓的情形

綜上所述，于股骨頭壞死的臨床診斷工作當(dāng)中，積極采用磁共振技術(shù)，可顯著提高患者病情確診的幾率，讓患者能夠及早接受對(duì)癥治療，從而有助于減少其致殘的風(fēng)險(xiǎn)，提高生活質(zhì)量，建議在臨床上進(jìn)行推廣和使用。

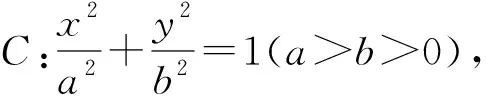
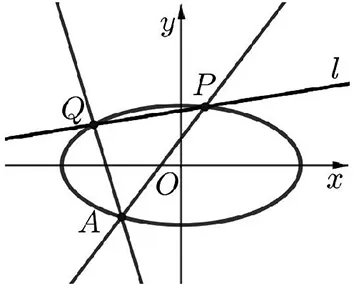
圖1

本文僅以焦點(diǎn)在x軸上的圓錐曲線為例進(jìn)行證明，其他對(duì)稱情形不再累述.

證明：由題意，直線AP、AQ的斜率都存在，且直線l不經(jīng)過(guò)點(diǎn)A(x0，y0).

(二)雙曲線與拋物線的情形

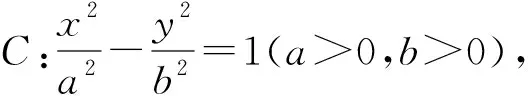
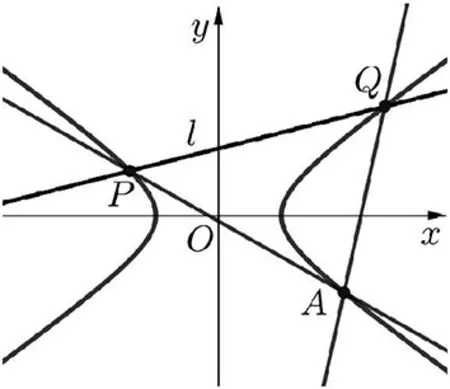
圖2

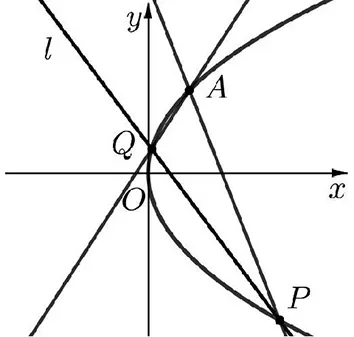
圖3

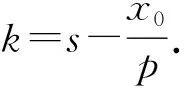
圖4

拋物線(焦點(diǎn)在y軸)的這種特殊情況，因異于文章研究?jī)?nèi)容，僅予以說(shuō)明，感興趣的讀者可自證.證明方法可參考定理1的證明；讀者亦可用焦點(diǎn)在y軸上的圓錐曲線統(tǒng)一方程來(lái)尋求原因.

既然三種圓錐曲線中都有一般的公式，圓錐曲線有運(yùn)用離心率的統(tǒng)一定義、方程，如果從統(tǒng)一的角度進(jìn)一步考慮這個(gè)問(wèn)題，我們堅(jiān)信：應(yīng)該會(huì)有統(tǒng)一的結(jié)論.

(三)圓錐曲線的一般情形

根據(jù)圓錐曲線的統(tǒng)一方程：(1-e2)x2+y2-2pe2x-p2e2=0(當(dāng)01時(shí)，表示雙曲線；當(dāng)e=1時(shí)，表示拋物線)，我們得到一般結(jié)論：

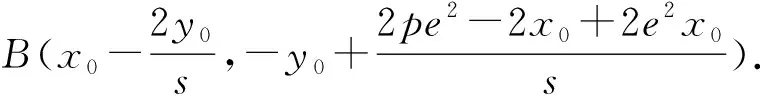
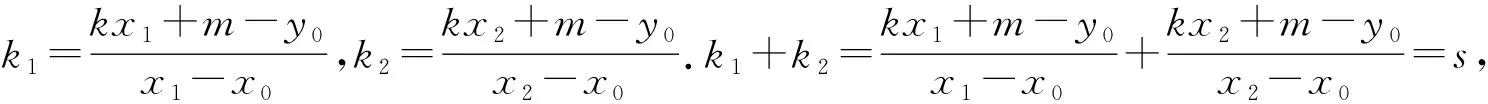
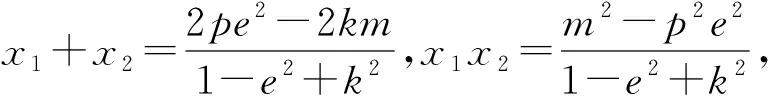
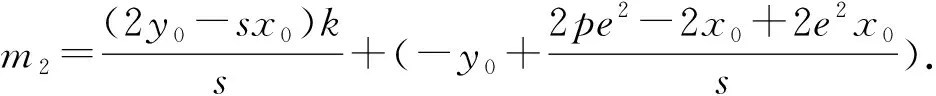
且可以容易計(jì)算得到：