“排隊問題”教學嘗試與拓展

陳方勇 劉靜 方佳雯

【摘 要】 《義務教育數學課程標準（2022年版）》將綜合與實踐作為數學學習的一個重要組成部分，這是初中生積累數學活動經驗，發展數學應用意識的重要載體.本文利用數學等式和不等式，結合問題假設，通過列表、邏輯推理、公式演算等數學方法，得出排隊問題中關于“等待時間”的一般性結論.嘗試在教學過程中融入數學核心素養、展現中華民族文化自信、樹立家國情懷等思政內容，幫助中學生樹立正確的世界觀、人生觀和價值觀.

【關鍵詞】 綜合與實踐；排隊問題；等待時間；思政教育

0 引言

《義務教育數學課程標準（2022年版）》指出，數學課程要培養的學生核心素養，主要包括：會用數學的眼光觀察現實世界；會用數學的思維思考現實世界；會用數學的語言表達現實世界.排隊是我們生活中常見的一種行為秩序，自覺排隊是個人素質修養和社會文明的體現，例如排隊就餐、排隊買票、排隊核酸檢測等.排隊現象中“等待時間”的長短是服務機構和服務對象（顧客）都關注的問題.數學家華羅庚曾經說過，“宇宙之大，粒子之微，火箭之速，化工之巧，地球之變，生物之謎，日用之繁，無處不用數學.”本文將利用數學的符號和語言，通過列表，構建等式與不等式等方式探討生活實際問題——排隊問題.我們先來看滬科版義務教育教科書（數學，七年級下冊，2013年版）中的2個問題.

問題1 某服務機構開設了一個窗口辦理業務，并按顧客“先到達，先服務”的方式服務，該窗口每2min服務一名顧客.已知當窗口開始工作時，已經有6位顧客在等待，在窗口開始工作1min后，又有一位“新顧客”到達，且預計以后每5min都有一位“新顧客”到達.

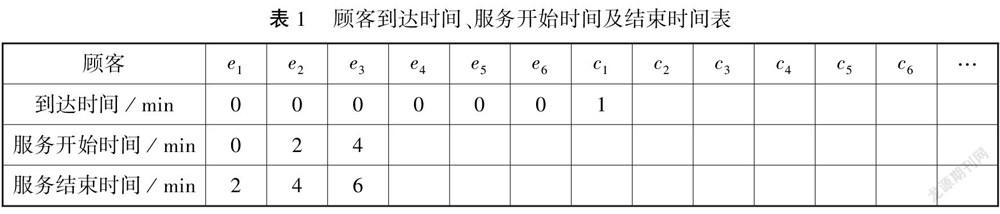
（1）設e1，e2，…，e6表示當窗口開始工作時已經在等待的6位顧客，c1，c2，…，cn表示在窗口開始工作以后，按先后順序到達的“新顧客”，請將下面表1補充完整（這里假設e1，e2，…，e6的到達時間為0）.

（2）下面表示每一位顧客得到服務之前所需要等待的時間，試將該表2補充完整.

（3）根據上述兩個表格，能否知道“新顧客”中，哪一位是第一位到達服務機構而不需要排隊的？求出他的到達時間.

（4）在第一位不需要排隊的顧客到達之前，該窗口已經服務了多少位顧客？為這些顧客服務共花費了多少時間？

（5）平均等待時間是一個重要的服務質量指標，為考察服務質量，問排隊現象消失之前，所有顧客的平均等待時間是多少？

問題2 在問題1的條件中，當服務機構的窗口開始工作時，如果已經有10位顧客在等待（其他條件不變），且當“新顧客”Cn離去時，排隊現象就此消失了，即Cn+1為第一位到達后不需要排隊的“新顧客”，問：

（1）用關于n的代數式來表示，在第一位不需要排隊的“新顧客”Cn+1到達之前，該窗口已經服務了多少位顧客？為這些顧客服務共花費了多長時間？

（2）用關于n的代數式來表示Cn+1的到達時間.

（3）根據（1）和（2）得到的代數式以及它們的數量關系，求n+1的值.

李慶銀［1］對以上兩個問題進行了探究，借助字母，利用幾個變量之間的關系，雖然得到核心不等式：第n人服務結束時間≤第（n+1）人到達時間，但是沒有進行深層次的分析與推廣.本文將從實際背景出發，通過抽象問題具體化、具體問題一般化、一般問題系統化三個遞進過程對排隊問題進行分析并推廣，以期對同學們后續課程學習、數學方法指導方面提供必要的幫助.

1 抽象問題具體化

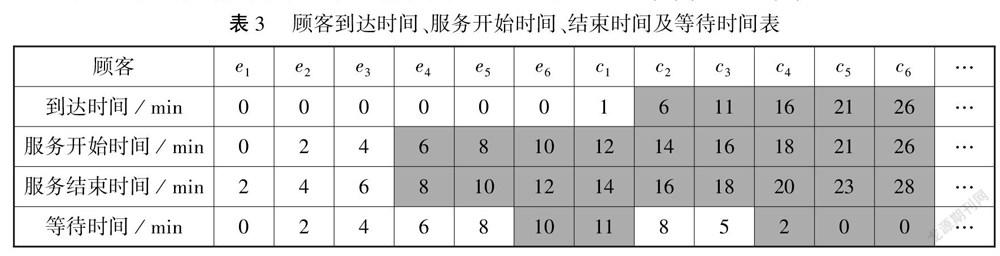
排隊問題實際背景雖然來源于生活實踐，但是假設條件多，具體時間概念之間關系緊密且抽象復雜.問題1直接通過表格形式利用“抽象問題具體化”方法，讓學生對抽象復雜問題有直觀的感知，從遞推關系中找到彼此的聯系，從而降低了題目的難度，簡化了解決問題的步驟.表格中可以發現“到達時間”“服務開始時間”“服務結束時間”“等待時間”的具體數值及數量關系，其中“等待時間”=“服務開始時間”-“到達時間”.特別地，因為窗口每2min服務一位顧客，而每5min才有一位“新顧客”到達，因此必然會出現窗口服務完某位顧客后等待新顧客到來的情況，并且在第一位無需等待的“幸運”“新顧客”之前，“服務開始時間”=前一個顧客“服務結束時間”，而在這位“幸運”顧客之后，每位顧客“服務開始時間”=“到達時間”.因此，利用表格將抽象問題具體化，理清各個時間概念之間的數量關系是解決問題的關鍵.

根據以上分析，容易補充（陰影部分）完成表3，解決問題1（1），問題1（2）.

由上述表格，不難得出如下答案：

問題1（3）顧客C5是第一位到達服務機構而不需要排隊的顧客，他到達的時間是21min.

問題1（4）在第一位不需要排隊的顧客到達之前，即C5之前，窗口已經服務了10位顧客，為這些顧客服務共花費了10×2=20（min）.

問題1（5）所有顧客平均等待的時間是（2+4+6+8+10+11+8+5+2）÷10=5.6（min）.

以上解決問題過程中，通過表格使用“抽象問題具體化”方法，幫助學生理清眾多時間之間的數量關系，清晰呈現彼此邏輯關系，可以讓一系列困難問題依次迎刃而解.下面將問題進一步深化，將到達時間、結束時間等概念進行字母化、模型化，進入問題2的分析與解決.

在問題2中，當服務機構的窗口開始工作時，已經有10位顧客在等待.于是，第一位不需要排隊的“新顧客”Cn+1到達之前，該窗口已經服務了（10+n）位顧客，服務這些顧客共花費2（10+n）min，即顧客Cn服務結束時間是2（10+n）min.根據題設和問題1表格中的結論，不難發現“新顧客”Cn到達時間是（5n－4）min，于是“新顧客”Cn+1到達時間為［5（n+1）－4］=（5n+1）min.Cn+1是第一位不需要排隊等待的顧客，說明Cn+1“等待時間”為0，即前一個顧客Cn的服務結束時間2（10+n）小于或等于Cn+1到達時間（5n+1）.通過構建一元一次不等式2（10+n）≤5n+1，解不等式得n≥193.所以n+1≥223，因為n+1為正整數，且Cn+1是第一位不需要排隊等待的顧客，所以n+1=8.因此，C8就是第一位到達后不需要排隊的“新顧客”，并且之后的每一位“新顧客”都無需排隊.

通過以上分析，不難得出問題2的所有答案，在此不作贅述.

2 具體問題一般化

結合問題1，問題2，為了得到更一般性的結論，提出問題3.

問題3 在問題1的條件下，假設當服務機構的窗口開始工作時，已經有m（m是正整數）位顧客在等待（其他條件不變），且當“新顧客”Cn離去時，排隊現象就此消失了，即Cn+1為第一位到達不需要排隊的“新顧客”，試分析m與n的關系式并求“新顧客”Cn等待的時間t.

分析 由于Cn+1是第一位不需要排隊等待的顧客，說明Cn+1到達時間大于或等于其前一個顧客Cn的服務結束時間.又因為Cn+1到達時間是（5n+1）min，Cn的服務結束時間是2（m+n）min.構建二元一次不等式，即為5n+1≥2（m+n），解不等式得，n≥2m-13，因為m，n都是正整數，所以n取大于或等于2m-13的最小正整數，則（n+1）取大于或等于2m+23的最小正整數，Cn+1是第一位不需要排隊等待的顧客.

“新顧客”Cn等待的時間t等于Cn服務開始時間與Cn到達時間的差，而Cn服務開始時間等于Cn-1服務結束時間，于是得到方程t=2（m+n－1）－（5n－4），化簡得，t=2m－3n+2.顯然當等待的時間t>0時，即2m－3n+2>0，解得n<2m+23，即“新顧客”Cn（n是滿足n<2m+23的最大正整數）就是最后一位需要排隊的顧客；其后一位顧客Cn+1就是第一位不需要排隊的顧客.

可以驗證問題1中，當m=6時，2m+23=143，即問題1中C5是第一位不需要排隊的顧客.

3 一般問題系統化、深刻化

排隊問題具有一般性，有必要將零散的認識系統化，將粗淺的認識深刻化、全面化，直到找到問題的本質規律.在具體應用中，必須根據實際問題轉換視角，運用逆向思維多角度考察問題.

問題4 在問題1的條件下，假設當服務機構的窗口開始工作時，已經有一群顧客在等待（其他條件不變），且當“新顧客”C10離去時，排隊現象就此消失了，即C11為第一位到達不需要排隊的“新顧客”，問：（1）窗口開始工作時，等待的一群顧客是多少人？（2）排隊現象消失之前，所有顧客的平均等待時間是多少？

分析 采用逆向思維，利用問題3的結論，滿足等待時間t>0時的最大正整數n對應的Cn即是最后一位需要排隊的“新顧客”；第二個問題不妨設等待的一群顧客（老顧客）是m人，則等待的時間分別是0，2，4，…，2（m－1），所以這m個“老顧客”等待的總時間是m（m－1）；而需要排隊的“新顧客”是10人，“新顧客”等待時間分別是t=2m－3n+2，n=1，2，…，10.結論，m個“老顧客”分別等待時間tm=2（m－1），等待的總時間Sm=m（m－1）；n個“新顧客”分別等待時間tn=2m－3n+2，等待的總時間Sn=n（2m－1）+12×（－3）n（n－1），m表示“老顧客”人數，其中n是小于2m+23的最大正整數.

解 設窗口開始工作時，等待的一群顧客是m人.由問題3的結論，Cn等待的時間t=2m－3n+2，令t>0，即2m－3n+2>0，當n=10時，可得m>14，因為C10是最后一位到達需要排隊的“新顧客”，所以m應取滿足m>14的最小整數，即窗口開始工作時，等待的一群顧客是15人.

由于“老顧客”人數m=15，所以“老顧客”分別等待時間為0，2，4，…，28min，“老顧客”等待的總時間是0+2+4+…+28=210（min）；10位“新顧客”分別等待時間29，26，…，2min，于是“新顧客”等待的總時間是29+26+…+2=155（min）；新老顧客總數是25人，于是排隊現象消失之前，所有顧客的平均等待時間是210+15525=14.6（min）.

顯然，顧客等待總時間也可直接使用公式計算，“老顧客”等待總時間是S15=15×（15－1）=210（min）；“新顧客”等待總時間為S10=10×（2×15－1）+12×（－3）×10×（10－1）=155（min）.

4 結語

（1）排隊是生活中的常見現象，本文通過抽象問題具體化，具體問題一般化，一般問題系統化、深刻化三個過程，以“等待時間”為突破口，通過問題引導，圖表制作，分析思考，邏輯推理、公式演算，構建一元一次不等式和二元一次不等式解決實際問題.整個探討過程情景代入感強烈，不斷吸引學生興趣的同時將排隊問題由易到難，由淺到深，逐層分析，使學生對問題更容易認識、理解和掌握.為學生以后學習探究綜合與實踐問題提供了研究方法與研究方向.

（2）對于排隊這一現實生活問題，我們先用數學的眼光去觀察它，進而用數學思維去思考分析，最后用數學的語言去表達，達到解決問題的目的.這與新課程標準中數學核心素養的理念相契合.

（3）自覺排隊是個人素質修養的體現，中國素有“文明古國，禮儀之邦”之稱，中學生更要養成自覺排隊的良好習慣.在本節課的教學過程中，教師應當主動引導學生樹立正確的世界觀、人生觀和價值觀，積極把思政教育貫穿教育教學全過程.

參考文獻

［1］吳之季，蘇淳.義務教育教科書數學七年級下冊［M］.上海：上海科學技術出版社，2013.

［2］李慶銀.排隊問題探究［J］.中學生數學，2018（12）：37-38.

作者簡介

陳方勇（1981—），男，安徽無為人，本科，中學高級教師;合肥市陳方勇名師工作室領銜人，享受合肥市政府特殊津貼，合肥市學科帶頭人，合肥市優秀教師;全國初中數學青年教師優秀課二等獎;主要研究初中數學課堂教學;發表20余篇論文.

劉靜（1990—），女，安徽合肥人，本科，中學一級教師，區優秀教師，優秀班主任;區課堂教學比賽一等獎;主要研究初中數學教學及數學學科與信息技術融合;發表多篇論文.

方佳雯（1993—），女，安徽桐城人，本科，中學二級教師;主要研究初中數學課堂教學.